對提高數學解題教學有效性的幾點思考

安徽省蒙城縣第六中學 (233500) 邵 源

當下,數學解題教學中,不少教師仍然采用“對答案”式的教學.實際上,“標準答案”看起來確實完美無瑕,但它不一定最適合學生的,學生只能感知“應該怎么做”,卻不知“為什么這樣做”,也不會思考“還能怎么做”,這樣不僅不會提高學生分析和解決問題的能力,而且會增加學生的課業負擔,與“減負增效”的教學目標背道而馳.就此,本文就解題教學有效性總結歸納了幾點教學建議,供參考.

一、構建知識網絡,為問題的解決提供思路

高考題重視考查學生綜合能力和綜合素養,因此一些中高檔的命題多在知識網絡的交匯處構思設計.要解決此類問題,需要以完善的知識體系為支撐.在解題教學中,教師應從整體的角度出發,關注知識點間的內在聯系,引導學生通過知識的遷移和重構來優化已有的認知網絡,讓學生學會根據已有知識網絡分析問題,以此提高學生解題能力.

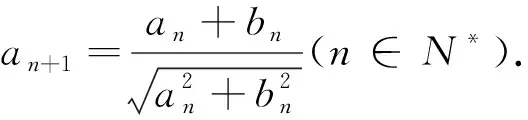
以上從不同角度出發,與函數、不等式、三角函數等相關知識聯系在一起,為問題的解決提供了合理的思路.

二、掌握通性通法,為問題的解決提供保障

一般地,高考所考查的是基礎知識、基本技能、基本方法,然部分教師為了追求速度,或者展現自己的教學能力,常常強化一些特殊方法,這樣學生記住了特殊方法卻忽視了通性通法.特殊方法在解決一些問題時確實高效,但是其缺乏一定的通用性,這樣過度強調特殊方法很容易將學生代入“死胡同”,影響解題效果.因此,在解題教學中,教師應重視通性通法的掌握,達到會一題通一類的效果,真正提高解決問題的能力.

例2 設a∈R,若x>0時,均有[(a-1)x-1](x2-ax-1)≥0,則a=.

這樣,將不等式恒成立問題轉化為函數問題,運用數形結合的思想方法順利地解決了問題.解題教學中,不僅要追求結果,更要追求過程,重視揭示問題的本質,重視強化學生的基礎知識、基本技能和基本方法,以此在夯實基礎的同時,優化認知,提升能力.

三、重視反思歸納,為問題的解決提供依據

在日常教學中,大多教師都遇到過這樣的困惑,有些問題反復講、重復做,但是學生在解題時依然會犯錯.出現這一現象的重要原因之一就是在平時教學中沒有進行反思和歸納,學習中出現似懂非懂的情況,從而影響解題效果.為了改變這一局面,教學中教師要預留時間讓學生進行總結歸納,爭取由掌握一道題變為掌握一類題,以此達到減負增效,融會貫通的效果.

例3 (1)當x>y>e時,求證:xy

其實,學生之所以會出現“懂而不會”、“一錯再錯”等情況,與教師的“教”息息相關.教學中,部分教師片面地追求速度,使得對數學知識、思想、方法等內容的挖掘不夠深入,并未觸及問題的本質,這樣學生在解題時很容易陷入囫圇之中,影響解題效果.在日常教學中,教師要既要關注思維的深度,也要重視思維的廣度,通過設計一題多變、一題多解,多解歸一等活動發散學生的數學思維,幫助學生積累數學活動經驗,優化學生的已有認知結構,提高學生解題能力.同時,在數學解題教學中,教師要預留時間和空間讓學生獨立思考、自主探究,引導學生利用已有的知識網絡主動分析問題,學會用變化的眼光看待問題,合理應用解題方法解決問題,以此通過多角度、全方位地分析來把握問題的本質,在鞏固學生已有知識和已有經驗的基礎上,提高學生數學能力和數學學力,提升學生數學素養.