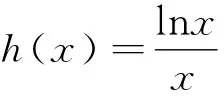例說一類含參數零點問題的解法

安徽省宿州市碭山中學 (235300) 毛曉偉 王 義

函數零點問題一直是高考中的熱點和難點,尤其是當其與導數結合起來時,解題方法更顯得靈活多變,難度不容小覷,筆者認為,函數零點問題的基本解決思路及方法可歸納如下:

首先研究函數f(x)單調性——自然要借助函數f(x)的導函數f′(x)(或f″(x))——這就需要知曉f′(x)的正負——往往要利用導函數f′(x)的零點——或隱零點——利用“隱零點”時則需借助“變形+構造”或“變形+放縮+構造”等方法來實現解題目的.

本文結合我校近期一道含參數零點問題的月考試題為例,一題多解,拋磚引玉.

一、試題呈現

已知函數f(x)=ln(x+1)-x+1.(1)求函數f(x)的單調區間;(2)設函數g(x)=aex-x+lna,若函數F(x)=f(x)-g(x)有兩個不同零點,求實數a的取值范圍.

二、解法探究

第(1)題略;本文重點討論第(2)小問.

思路1:隱零點視角

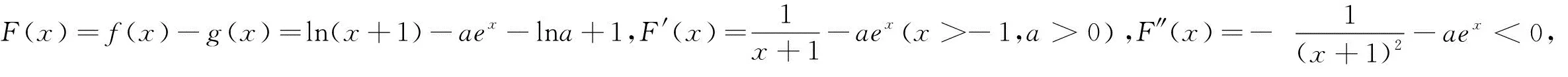
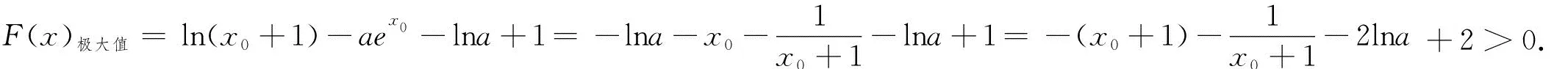
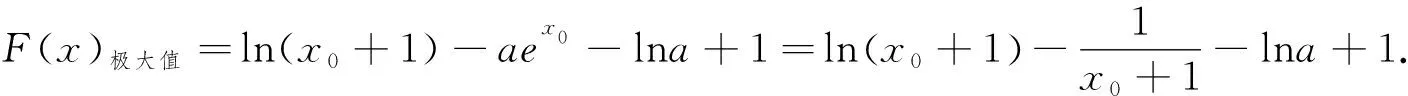
點評：本題由于函數F(x)復雜,直接分類討論,參變分離,參變半分離等基本方法行不通,故先求導,再求單調區間,極大值,轉化求函數F(x)極大值大于零,運用隱零點設而不求,消元轉化,解法1全部消參換元,進而求函數最值,解法2部分消參,利用不等式放縮,求解最值,解法3部分消參,直接分類討論求參數的取值范圍.

思路2:同構視角

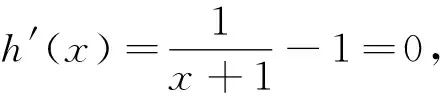
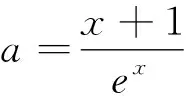
點評：解法4,解法5從函數F(x)整體入手,觀察分析,可變形為ln(x+1)+x+1=aex+x+lna,由對數恒等式可知,aex=elna+x,x+1=eln(x+1),x+lna=lna·ex,則可構造h(x)=ex+x或h(x)=x+lnx在利用函數單調性將問題轉化為可分離參數類型的簡單函數,進而求出參數a的取值范圍.

思路3:構造函數視角

點評：解法6參數半分離,轉化兩個互為反函數交點個數問題,進而轉化為與函數y=x有兩個不同交點問題,在利用函數單調性將問題轉化為可分離參數類型的簡單函數,進而求出參數a的取值范圍.