不相稱分數階統一混沌系統的滑模同步

周衛光，鄭永愛

（揚州大學信息工程學院，江蘇 揚州 225127）

近年來，人們在整數階混沌系統的理論基礎上開始對分數階系統展開研究。通過研究發現，許多分數階系統也存在混沌現象，如分數階Chen 系統[1]，分數階離散Lorenz 系統[2]，分數階時滯Lü系統[3]，分數階統一混沌系統[4-6]，分數階金融系統[7]和分數階Genesio-Tesi 系統[8]等。與此同時，分數階混沌系統的控制和同步也取得了很大的進展，各種各樣的混沌同步控制方法被相繼提出，如滑模控制[9]、自適應控制[10-11]、無源控制[12]和主動控制[13]等。

分數階統一系統將分數階Lorenz 系統、分數階Lü系統和分數階Chen 系統聯系起來。由于分數階統一系統包含了混沌動力學的許多特征，因此很多學者對其進行研究，并取得了一些研究成果。文獻[14]基于無源控制理論，設計一種能夠使分數階統一混沌系統穩定的無源反饋控制器。文獻[15]設計了一種實現分數階統一混沌系統函數投影同步的自適應控制器。但這些控制和同步方案都未考慮分數階統一混沌系統存在的外部未知擾動。文獻[16]利用分數階擾動觀測器對分數階金融系統存在的外部未知有界擾動進行估計，結合分數階擾動觀測器設計了自適應滑模同步的控制方案，實現了分數階金融系統的有界混合投影同步。然而文獻[16]所設計的分數階擾動觀測器只能使擾動誤差是有界的，而不能使擾動誤差漸近趨于零，并且也只是實現了分數階金融混沌系統的有界混合投影同步，而不是漸近同步。

針對以上問題，筆者首先設計了一種新的分數階擾動觀測器來估計分數階統一混沌系統的外部擾動，該分數階擾動觀測器能使擾動誤差漸近趨于零；然后結合所提出的分數階擾動觀測器構造分數階積分滑模面并設計了合適的自適應滑模控制器，實現了具有未知干擾、不相稱分數階統一混沌系統的漸近同步控制；最后數值模擬驗證了該方法的有效性。

1 系統描述與分數階導數

分數階導數的定義有多種，這里采用Caputo 定義來研究具有未知擾動的不相稱分數階統一混沌系統的同步問題。Caputo 導數定義為：

其中，n-1 ＜q＜n,n∈N，Γ(·)為伽馬函數：

不相稱分數階統一混沌系統[4]描述如下，并將其簡化為系統（1），以下簡寫類似：

其中，x1,x2,x3為狀態變量,q1,q2,q3∈(0,1) 為分數階。當α∈[0,0.8)時，系統屬于廣義不相稱分數階Lorenz 系統；當α=0.8 時，系統屬于廣義不相稱分數階Lü系統；當α∈(0.8,1]時，系統屬于廣義不相稱分數階Chen 系統。設q1=0.991，q2=0.992，q3=0.993；初始條件為x(0)=[5,8,10]T，分數階統一混沌系統的混沌吸引子如圖1、圖2 和圖3 所示。

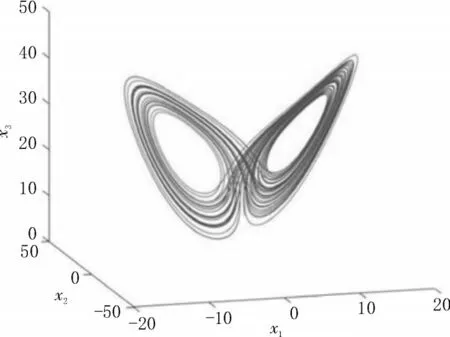
圖1 α=0 時，分數階Lorenz系統混沌吸引子

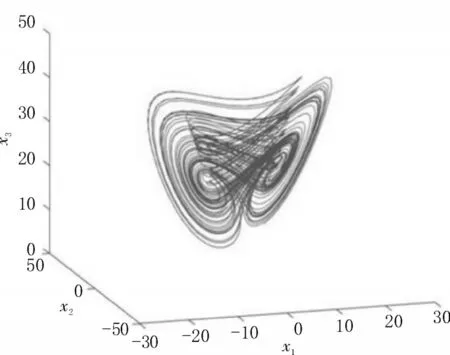
圖2 α=0.8 時，分數階Lü系統混沌吸引子

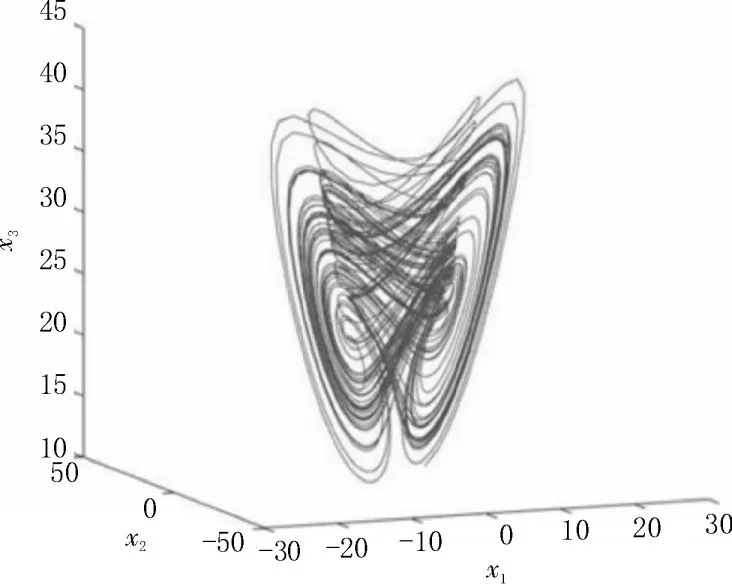
圖3 α=1時，分數階Chen系統混沌吸引子以系統(1)為驅動系統，相應的具有未知擾動的響應系統為：

其中，y1,y2,y3為狀態變量,d(t) 為外部未知擾動，q1,q2,q3∈(0,1)，u(t)為控制輸入。

定義誤差變量ei=yi-xi,i=1,2,3，得到誤差系統：

引理1對于分數階線性系統：

其中，q∈(0,1)，x∈Rn，A∈Rn×n，若矩陣A的特征值λi滿足，則分數階系統(4)的零點是漸近穩定的。

引理2設x(t)∈R是一個連續可導的函數，那么對于任意時間t≥t0且0 ≤q≤1，有：

引理3設V(t)函數如下：

其中，y1(t)∈Rn和y2(t)∈Rn具有連續的一階導數，Q1∈Rn×n和Q2∈Rn×n為兩個正定矩陣。若存在正定矩陣Q3∈Rn×n和常數h0＞0 使得：

2 觀測器及滑模同步控制設計

2.1 分數階擾動觀測器的設計

為了實現驅動系統(1)與響應系統(2)之間的同步，控制目標選取合適的控制器u(t)，使得誤差系統(3)的零點是漸近穩定。然而由于外部擾動d(t) 未知，不能直接用于控制器u(t)的設計。為了克服這一問題，首先設計一個分數階非線性擾動觀測器來估計未知擾動。在設計分數階擾動觀測器之前，引入假設1 如下：

假設1假設外部擾動d(t)的Caputo 分數階導數有界，即，其中ω是已知的正常數。

為了設計分數階非線性擾動觀測器，定義輔助變量：

其中，β是正常數。

輔助變量φ(t)的Caputo 分數階導數為：

由系統（2）中第二個等式和（9）得：

為了計算擾動估計，中間變量φ(t) 的估計描述為：

根據式（8），外部擾動d(t)的估計為：

定理1考慮擾動觀測器(11)和(12)，如果假設1的條件滿足，那么擾動估計誤差漸近收斂于零。

證明：根據式（8）、（12）得：

根據式（10）、（11）得：

根據引理2，Vd的Caputo 分數階導數為[18]：

將式（13）代入式（15）并根據假設1，得：

2.2 自適應滑模同步

為了讓研究能夠進一步開展，給出下面的假設2。

假設2假設存在未知正常數k，使得：

設計分數階積分滑模面為：

滑模控制器設計為：

自適應律為：

定理2在假設1 和2 的條件下，如果設計分數階擾動觀測器(11)和(12)，自適應滑模控制器(18)和(19)，那么誤差系統(3)的零點是漸近穩定的，即驅動系統(1)和響應系統(2)實現漸近同步。

證明：構造Lyapunov 函數：

根據引理2，Vs的Caputo 分數階導數為：

由控制器(18)和自適應律(19)有：

3 數值模擬仿真

利用Matlab 進行數值仿真，選取不相稱分數階q1=0.991,q2=0.992,q3=0.993，初始值x(0)=[5,8,10]T，y(0)=[-6,-8,-10]T，α=0，d(t)=4 cos(2t)，β=60，=0.1，λ=20，r=0.1，ω=0.01。所設計的分數階擾動觀測器(11)和(12)的擾動觀測結果和觀測估計誤差分別如圖4 和圖5 所示，這表明所設計的分數階擾動觀測器是有效可行的。

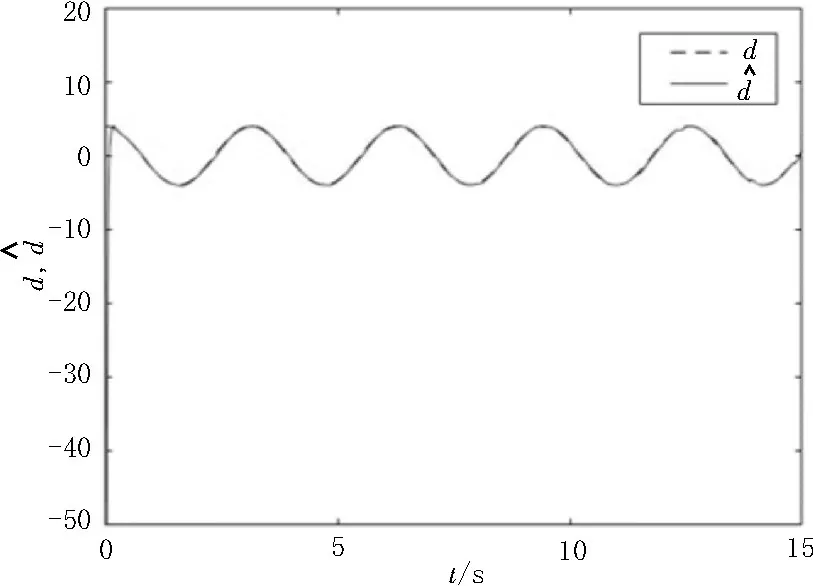
圖4 擾動d 和擾動估計的軌跡

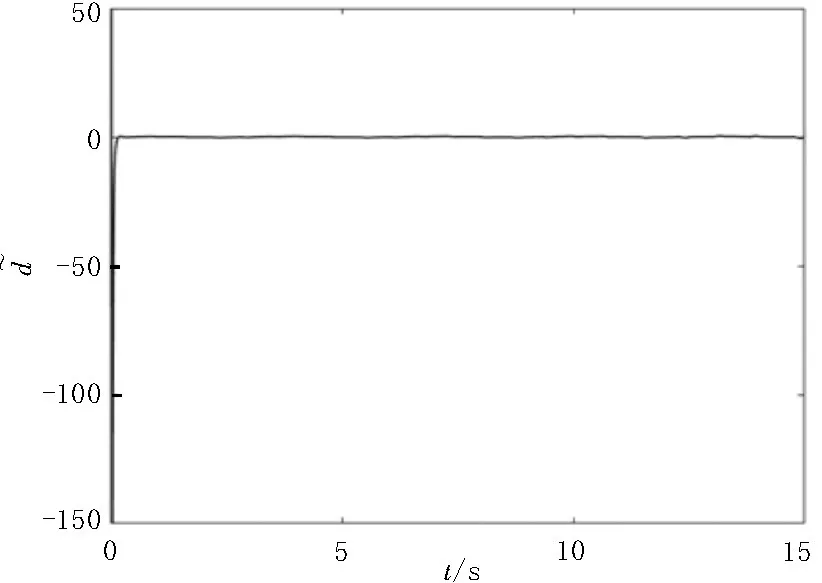
圖5 估計誤差的軌跡

應用自適應滑模控制器(18)和(19)后，驅動系統(1)和響應系統(2)的狀態響應如圖6 所示。同步誤差系統(3)的狀態響應如圖7 所示，誤差系統(3)漸近趨于零，驅動系統(1)和響應系統(2)實現漸近同步。滑模運動軌跡和未知正常數k的估計曲線分別如圖8和9 所示。

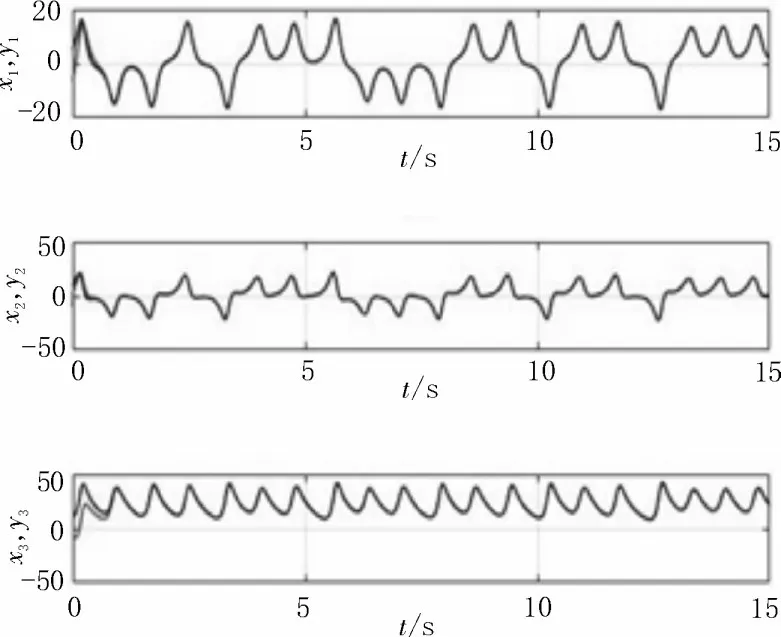
圖6 驅動系統與響應系統的狀態軌跡

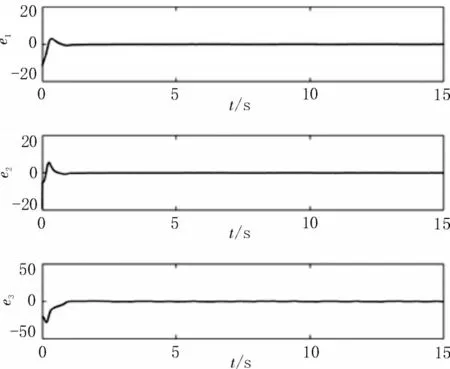
圖7 同步誤差與時間狀態軌跡

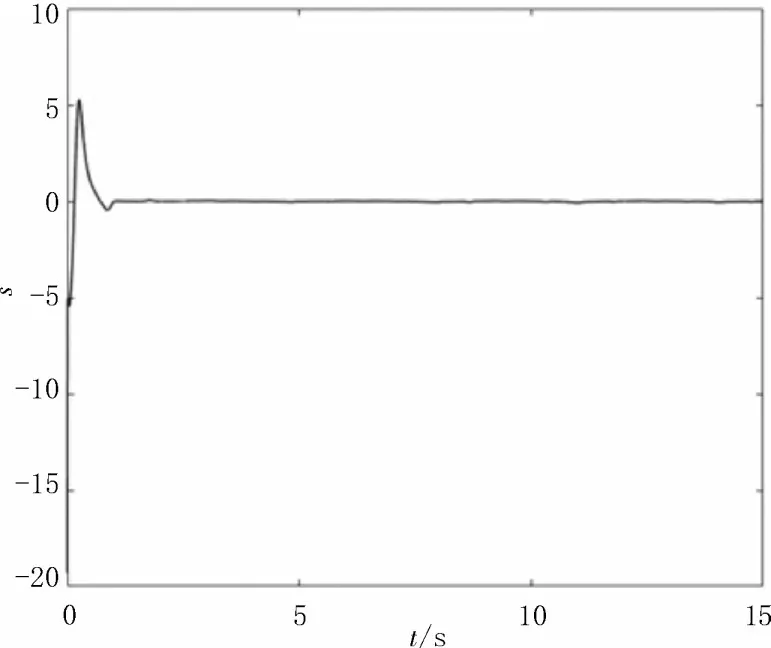
圖8 滑模運動s(t)的軌跡

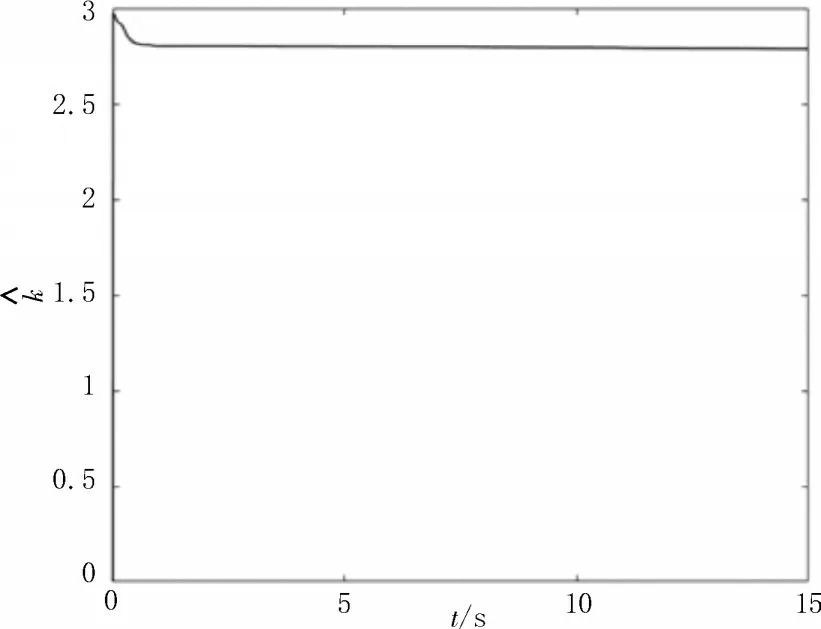
圖9 k 的估計曲線

4 結論

將含有未知擾動的不相稱分數階統一混沌系統作為研究對象，設計分數階擾動觀測器對系統中的外部擾動進行估計。基于Lyapunov 理論和自適應控制理論，設計合適的自適應滑模控制器，實現含有未知擾動的不相稱分數階統一混沌系統的漸近同步。