考慮主環境因素的GWO-SVR 風電功率超短期預測

徐煒君

（東北石油大學秦皇島校區電氣信息工程系，河北秦皇島 066004）

隨著“碳達峰碳中和”目標的提出，可再生能源的作用愈顯突出，我國可再生能源裝機規模持續擴大，截止到2021 年11 月底，我國風電裝機容量已躍居世界首位，約為3 億千瓦，同比增長29%，風電利用率達到了96.9%。但風自身的不穩定性，使得風力發電具有波動性、間歇性和非線性的特點，因而大規模的風電并網會對電網調峰、調頻和安全穩定運行帶來極大挑戰[1]。為了更加合理地利用風電，提高風電功率預測精度成為學界研究的熱點。

目前，國內外學者已經提出了許多成熟的風電功率預測方法，這些方法主要分為兩類：物理方法和統計方法。物理方法根據數值天氣預報和風機組自身信息以及周圍的物理信息構建出的物理模型進行預測[1]。統計方法主要是利用機器學習方法，諸如BP(Back Propagation)神經網絡、K 鄰近算法(K-Nearest Neighbor，KNN)、隨機森林（Random Forest，RF）、支持向量機（Support Vector Machine，SVM）、極限學習機（Extreme Learning Machine，ELM）等，對大量的風速、風向、溫度、氣壓等數據進行訓練和回歸預測，進而實現風電功率預測[2-4]，并且輸入數據維度越高，更有利于探索其動態變化規律[5]，但輸入數據維度越高，預測模型的復雜程度越大，預測的時間會增加，這不利于風電的超短期預測。

為此，文中在深入分析影響風機出力的主要環境因素的基礎上，對風電場的采樣數據進行了降維處理，并用GWO-SVR 預測模型進行預測分析，實驗結果對比表明，經過降維處理后，有效地降低了預測模型的復雜程度，降低了無用數據對預測結果的影響，GWO-SVR 預測算法在穩定性、預測時間及精度三個方面均有提高。

1 影響風機出力的主要因素分析

根據空氣動力學和貝茲準則可知，風機從風能中捕獲的功率可表示為[6]：

其中,P為風機的輸出功率，Cp(λ,β) 為葉片的風能利用系數，λ為葉尖速比；β為槳距角，A為風輪掃掠面積，單位為m2，ρ為空氣密度，單位為kg/m3，v為風速，單位為m/s。

1.1 風能利用系數對風機出力的影響

葉尖速比可表示為：

其中，ωm為風輪角速度，單位為rad/s；R為風輪半徑，單位為m，v為風速，單位為

葉片風能利用系數的一種解析計算方法為[7]：

綜合式（2）-（4）可知，風能利用系數為角速度ωm、槳距角β和風速v的相關函數，可記為：

葉尖速比λ由風速與風輪轉速決定，而當葉片一定時，葉片最佳槳距角β一定，因此對于一個風機來說，其風能利用系數僅與風速和風輪轉速有關，對于特定的風速，存在唯一的轉速使得Cp達到最大。而單從風電預測考慮，只要能夠準確預測出風速，通過對風機轉速的系統控制，就能夠得到Cp的最大值[8]。因此，單從風電預測考慮，風能利用系數主要與風速有關。

1.2 風輪掃掠面積對風機出力的影響

風輪掃掠面積是與風向垂直的平面上，風輪旋轉時葉尖運動所生成圓的投影面積，具體計算為：

其中，R為風輪半徑，單位為m，α為風向的垂直平面與風輪旋轉圓平面之間的夾角，0°≤α≤90°，由式（6）可以看出，風向是影響風機出力的主要因素之一。

1.3 空氣密度對風機出力的影響

由式（1）可知，風機的輸出功率與空氣密度成正比，而影響空氣密度的環境因素有氣壓、溫度、海拔高度和濕度[9]。根據風電場所處的不同地理環境，有些影響空氣密度的環境因素不需考慮，比如已經建設好的風電場，其海拔高度不變，因此可以不考慮海拔對空氣密度的影響。文中所涉及的風電場屬于這種情況，以下將分析氣壓、溫度和濕度對空氣密度的影響。

空氣密度與氣壓、溫度、濕度的關系可以表示為[10]：

其中，ρ為10 min 內的平均空氣密度，P為10 min 內測量的干燥空氣平均氣壓，R0為干燥空氣的氣體系數，取287.05 J/(kg·K)，T為10 min 內的平均測量溫度，T=Tc+273.15，Tc為實際溫度。Pv的計算如式（8）所示：

其中，C0=6.107 8,C1=7.5,C2=237.3，均為特滕斯公式（Tetens Formula）的系數。PH%為相對濕度，定義為實際水蒸氣壓力和飽和水蒸氣壓力的比值。

綜合式（7）-（8）可以看出，氣壓、溫度、濕度的變化都會引起空氣密度的變化。為了進一步分析其變化規律，分兩種情況：

1）濕度一定，氣壓和溫度對空氣密度的影響如圖1 所示。從圖1 可以看出，隨著氣壓降低和溫度升高，空氣密度會變小。

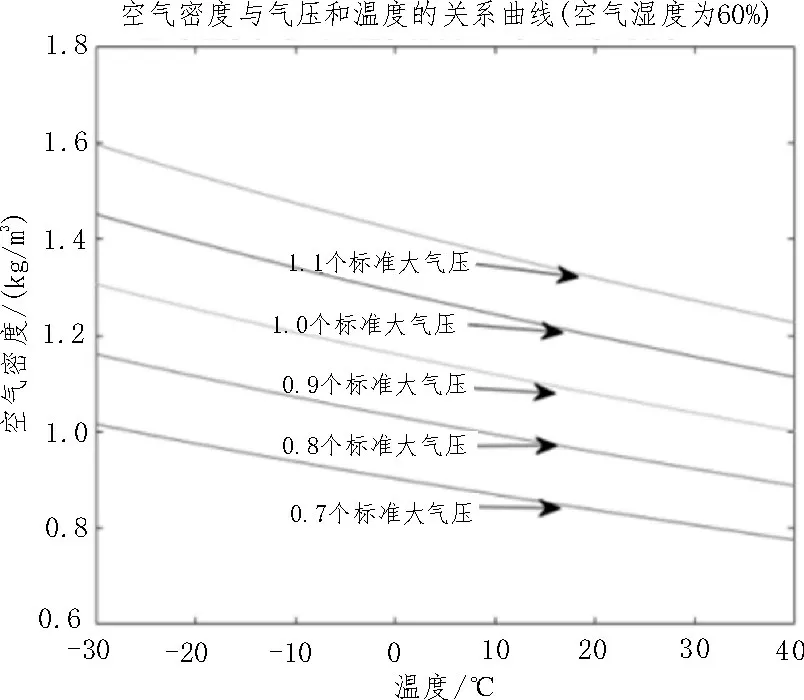
圖1 空氣密度與氣壓、溫度的關系

2）氣壓一定，濕度和溫度對空氣密度的影響如圖2 所示。從圖2 可以看出，在氣壓一定且溫度較低時（如-20 ℃），濕度的劇烈變化對空氣密度的影響不大；而在高溫區域（如+30 ℃左右），隨著相對濕度的增加，空氣密度會降低。濕度和溫度對空氣密度影響的整體趨勢是：隨著相對濕度變大和溫度升高，空氣密度將會變小。

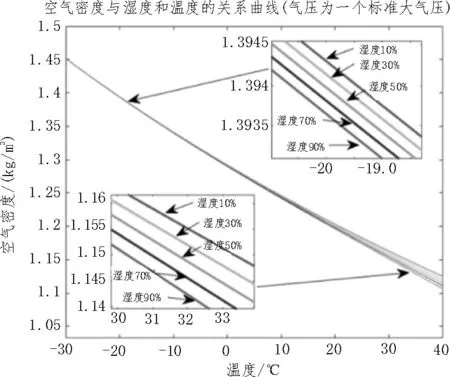
圖2 空氣密度與濕度、溫度的關系

綜上，在一個固定的風電場，溫度、氣壓和濕度的變化會影響空氣密度的變化，進而影響風機出力，因此，在進行風電預測時應該考慮溫度、氣壓和濕度三個環境因素的影響。

通過上文分析可以看出，影響風機出力的主要環境因素有溫度、濕度、氣壓、風向和風速，在進行風電預測時，應該重點關注這幾個環境因素。

2 風電場數據建模及降維處理

風電場一般由若干臺風機組成，各風機的分布需要根據地勢、尾流效應及主風向等因素而定，同時由于風能隨機波動性的影響，風電場中各風機的出力不能隨時與風力相匹配，因此風電場的風電功率預測應從全局出發，應著重考慮整個風電場的風電特性，而風電場中的測風塔最能反映這一特性[11]。目前業界比較認可的風電功率預測有兩種方法：一是先預測風速，然后根據風電場的功率曲線得到風電場的輸出功率；二是直接預測其輸出功率[11]。文中采用第一種方法。

2.1 風電場數據建模

以新疆昌吉州某風電場測風塔的歷史監測數據進行數據建模。該風電場的平均海拔高度為967 m，地形以戈壁為主，風機主要為2.2 MW 風機，高度為80 m，測風塔塔高為70 m。測風塔可分別測量70 m、50 m、30 m 和10 m 高處的風速及風向，7 m 高處的氣壓、溫度和濕度，其數據采集以10 min 為間隔，每1 s采集一次數據，并對10 min 的600 個數據進行統計分析，計算出平均值、最大值、最小值和標準差。每一個10 min 間隔可以得到一個44 維的向量。

考慮到風電場當地每年四五月份的氣候變化比較劇烈，因此選用2020 年4 月26 日—5 月5 日10 天的日監測數據作為建模數據，每天以10 min 為間隔進行數據采樣，最終得到一個1 440×44 的樣本集。為了使各維分量在實際的預測過程中具有相同的地位，必須將這些量綱、取值范圍各不相同的數據使用歸一化方法變換到同一范圍，歸一化方法為：

其中，i=1,2,…,1 440，j=1,2,…,44，yi(j) 為實際分量，max[yi(j)]、min[yi(j)]分別為第j個分量的最大和最小值，xi(j)為歸一化后的分量值，歸一化后數據的取值范圍均為[-1,1]。

2.2 風電場數據降維處理

如果用2.1 得到的1 440×44 的數據作為預測模型的訓練和測試樣本集，由于該數據維度較高，會嚴重影響預測模型的運算速度和精度，因此需要對數據進行降維處理。

通過第1 節的分析可知，風速和風向是影響風機出力的主要因素，因此在數據降維處理時必須考慮這兩種因素。風速及風向的最大值和最小值只能反映該時間段內的極值分布，其標準差反映數據的分散程度，而風速及風向的平均值可以反映其在某一個時間段的趨勢，同時考慮到影響風機出力的主風速應該和風機高度相當，所以選用70 m 高處的風速及風向的平均值作為建模數據。

風速是地形、海拔、氣壓、濕度、溫度等多種因素共同作用的結果[12]，同時氣壓、濕度、溫度的變化會引起空氣密度的變化，進而影響風機出力。假定在相鄰的采樣周期內（20 min 內），風速和風向不變，風機出力只與空氣密度有關，用式（7）和式（8）計算每個采樣周期（氣壓、濕度、溫度用平均值）的空氣密度，并用式（10）計算相鄰采樣周期的空氣密度變化率：

其中，ρi為第i個采樣周期的空氣密度，i=1,2,…,1 439，Rρi最大變化率為1%，出現在4 月27日上午9：50-10：00 和10：00-10：10 這兩個相鄰的采樣間隔，十天內變化率大于0.5%的相鄰時刻有9 次，說明短時內空氣密度也會有大的波動，因此結合該風電場的實際，應將氣壓、溫度和濕度作為建模數據。通過上述降維處理，將原來的44 維數據降為了風速、風向、氣壓、溫度和濕度5 維數據，這樣可以極大地提高計算速度。

進一步分析1 440×5 樣本數據發現，該樣本集中氣壓的變化最小。將每維1 440 個數據分成240 份，每份6 個數據，對應一個小時的數據，對240 份（小時）數據分別求數據的標準差，得到圖3 所示的標準差比較曲線。從圖3 可以看出，與其他天氣因素比較，在某段時間內氣壓的標準差幾乎不變或者變化非常小，說明其數據比較集中，波動性較小，因此在實際的預測分析中可以不考慮氣壓的影響，這樣可以將1 440×5 樣本集進一步降為1 440×4 樣本集，進一步提高計算速度，降維過程充分考慮了影響風機出力的主要因素，同時也考慮了風速、風向、溫度和濕度之間的相互影響和聯系。

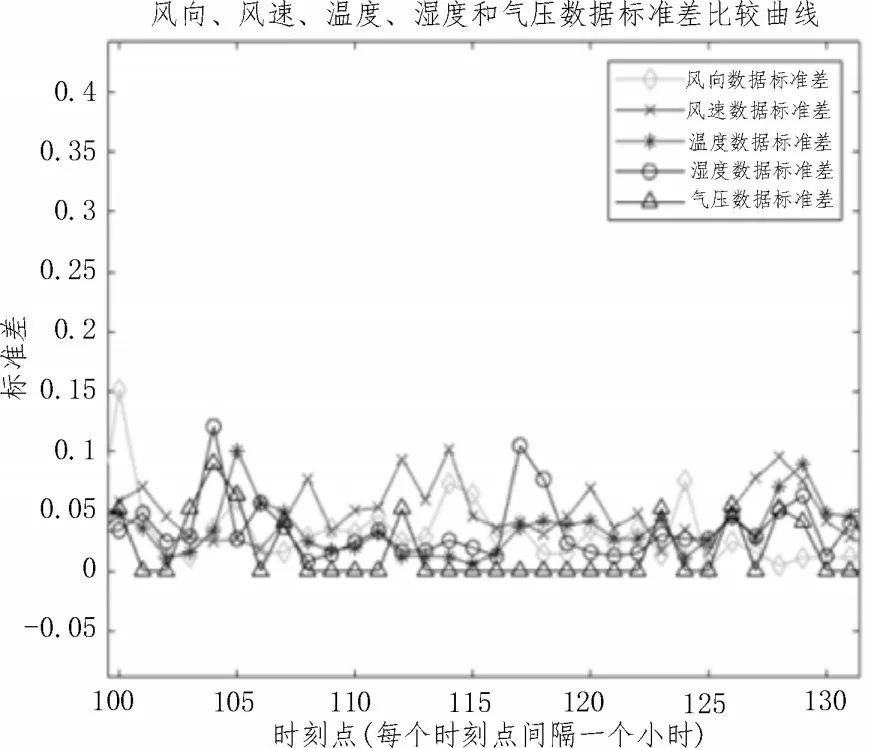
圖3 氣象數據標準差比較曲線

3 GWO-SVR預測模型設計

3.1 支持向量回歸機（SVR）

支持向量回歸機（SVR）由Vapnik 于1995 年首次提出，其核心思想是通過引入非線性映射φ(x)，實現樣本空間從低維到高維的變換，通過在高維空間的線性回歸得到原樣本的非線性特性[13]，其映射關系表示為：

核函數類型的選取會直接影響回歸結果，同時考慮到核函數參數的數量對預測模型復雜程度的影響，文中選擇能夠實現非線性映射的徑向基函數（Radial Basis Function，RBF）作為SVR 的核函數，其表達式為：

其中，σ為待確定的核函數參數。由式（12）、（13）可知,只要選取合適的C、ε、σ便可以確定SVR 的具體形式，從而對控制對象進行準確預測[13]。在實踐中發現，ε值的選取獨立于C、σ的選取，因此可以根據SVR 的建模精度先確定ε，再優化參數C、σ，這樣可以降低參數優化的復雜程度[13]。

3.2 灰狼優化算法

灰狼優化算法(Grey Wolf Optimizer,GWO)是澳大利亞學者Mirjalili 于2014 年受灰狼捕食行為的啟發，提出的一種群智能優化算法[14-15]。GWO 算法將狼群分為α、β、δ、ω四種類型：α狼是領導者（最優解），β狼和δ狼協助α狼對狼群的進行管理及捕獵過程中的決策，同時也是α狼的候選者，ω狼主要協助α、β、δ對獵物進行攻擊。當狼群包圍獵物時，狼群的位置變化由以下數學模型定義：

其中，t為當前迭代，A和C為協同向量，Xp(t)為獵物的位置向量，X(t)為灰狼的當前位置向量。A、C的計算如下：

其中，a在迭代過程中線性遞減且遞減范圍為[2,0]，r1、r2是[0,1]范圍內的隨機向量。

根據狼的狩獵行為，將前三個最優值保存為α、β和δ，然后灰狼種群的位置更新公式如下：

其中，Dα、Dβ、Dδ分別表示α、β和δ狼和其他狼之間的距離，Xα、Xβ、Xδ分別是α、β和δ狼的當前位置，C1、C2、C3是隨機向量，X是當前灰狼的位置。式（17）、（18）通過a值的遞減來實現迭代，最終可得最優解。

3.3 GWO-SVR預測模型的構建

GWO-SVR 預測模型的構建流程如圖4 所示，主要步驟為：

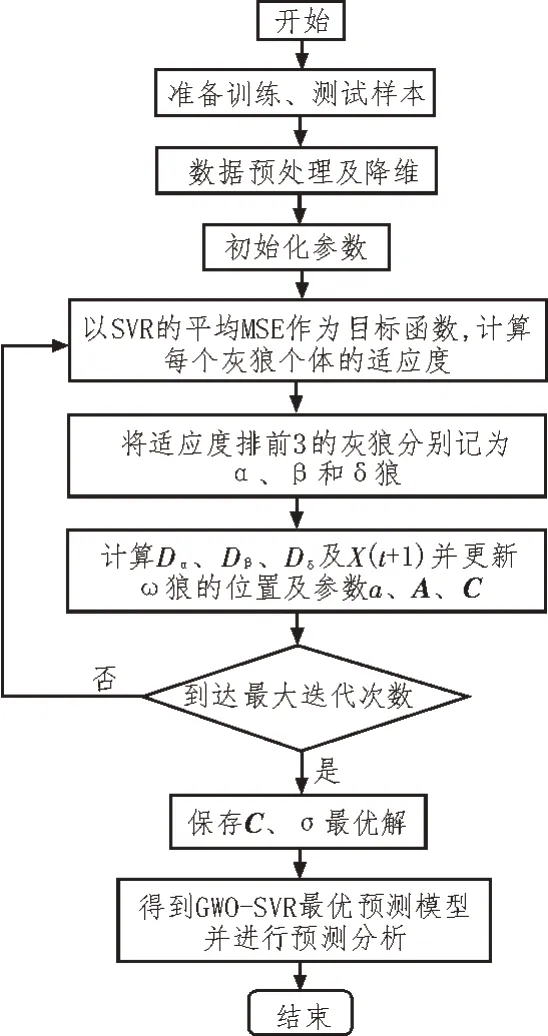
圖4 GWO-SVR預測模型流程圖

1）取前9 天的數據（4 月27 日-5 月4 日）作為訓練樣本，第10 天（5 月5 日）的數據作為測試樣本，并對訓練和測試數據進行預處理和降維。

2）初始化參數：狼群數量為20，最大迭代次數為100，參數C、σ的上下界均為[0.01,100]，α、β和δ狼的初始位置均為(0,0)。

3）以SVR 的平均均方誤差MSE 作為目標函數，計算每個灰狼個體的適應度，并將適應度排前3 的灰狼位置記為Xα、Xβ、Xδ。

4）依據式（17）、（18）計算Dα、Dβ、Dδ及X(t+1)，并更新ω狼的位置及參數a、A、C。

5）判斷是否到達最大迭代次數，如達到則保存C、σ最優解，否則返回步驟3）。

6）得到GWO-SVR 最優預測模型并進行預測分析。

4 實驗仿真與分析

以3.2 節得到的樣本集為例，進行仿真與分析。為了驗證經過降維處理后，可以提高預測的精度及速度，分別建立GA-SVR、PSO-SVR、GWO-SVR 三種預測模型，并對不同維度的樣本集用這三個模型分別進行預測分析，采用均方根誤差(RMSE)及衡量擬合度的復測定系數R2作為預測模型的評價指標[16-18]。

采用以下六種不同維度的樣本集作為訓練和測試集，分別用GA-SVR、PSO-SVR、GWO-SVR 三種預測模型預測70 m 處的平均風速，得到的預測結果如表1 所示。

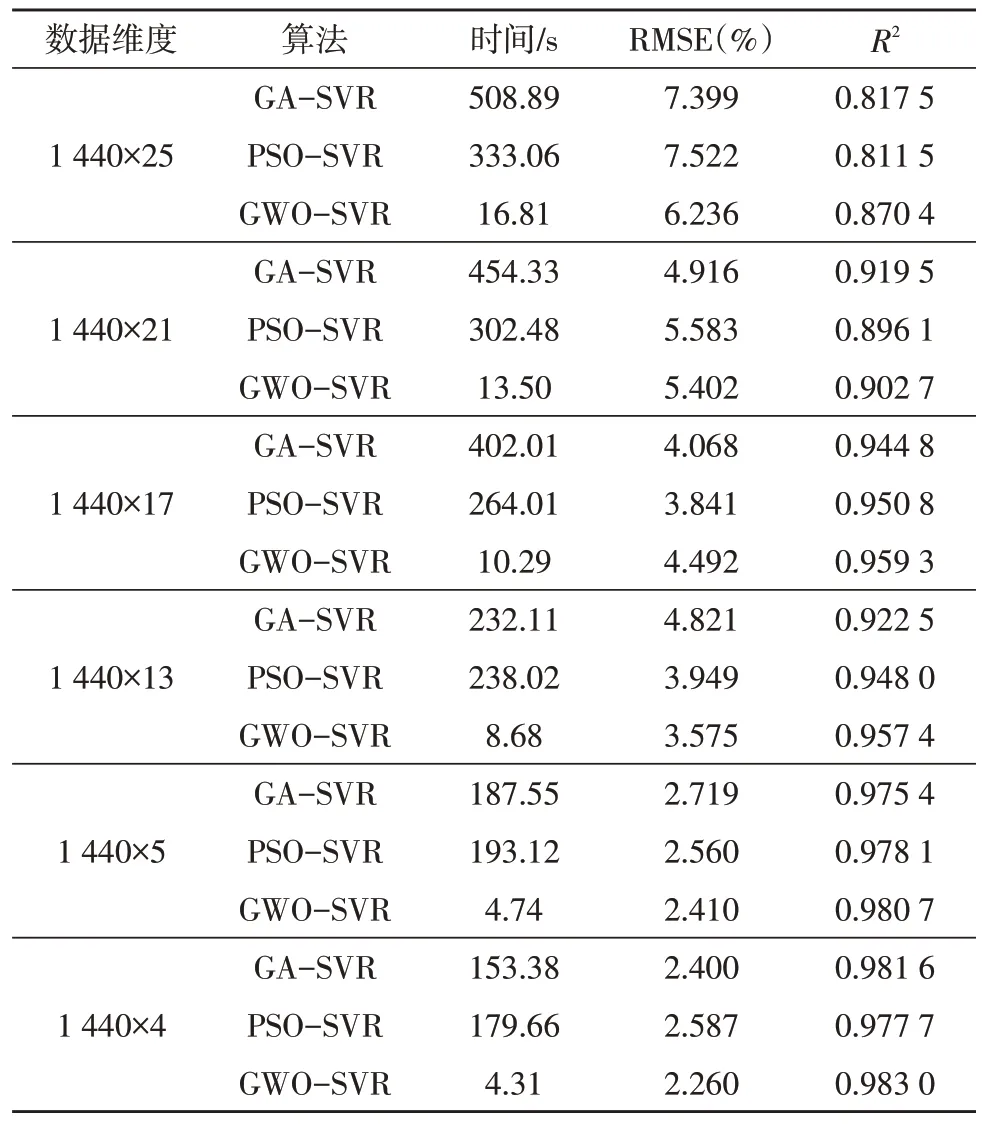
表1 不同算法在不同數據維度下預測結果

1）1 440×25：70 m、50 m、30 m、10 m 處風速及7 m處氣壓、溫度、濕度的平均、最大和最小值，70 m、50 m、30 m、10 m 處風向的平均值。

2）1 440×21：70 m、50 m、30 m 處風速及7 m 處氣壓、溫度、濕度的平均、最大和最小值，70 m、50 m、30 m 處風向的平均值。

3）1 440×17：70 m、50 m 處風速及7 m 處氣壓、溫度、濕度的平均、最大和最小值，70 m、50 m 處風向的平均值。

4）1 440×13：70 m 處風速及7 m 處氣壓、溫度、濕度的平均、最大和最小值，70 m 處風向的平均值。

5）1 440×5：70 m 處風速及7 m 處氣壓、溫度、濕度的平均值，70 米處風向的平均值。

6）1 440×4：70 m 處風速、風向及7 m 處溫度、濕度的平均值。

從表1 可以看出，隨著數據維度的降低，三種算法的預測時間都在減少，預測能力也逐漸增強（RMSE 逐漸減小），擬合度也越來越好（R2逐漸變大）。但是這三種算法的預測能力存在較為顯著的差別，圖5、6、7 分別為各算法的預測時間、RMSE 及R2的比較曲線。圖8 為三種算法在1 440×4 維度下預測的70 m 處平均風速的比較曲線。

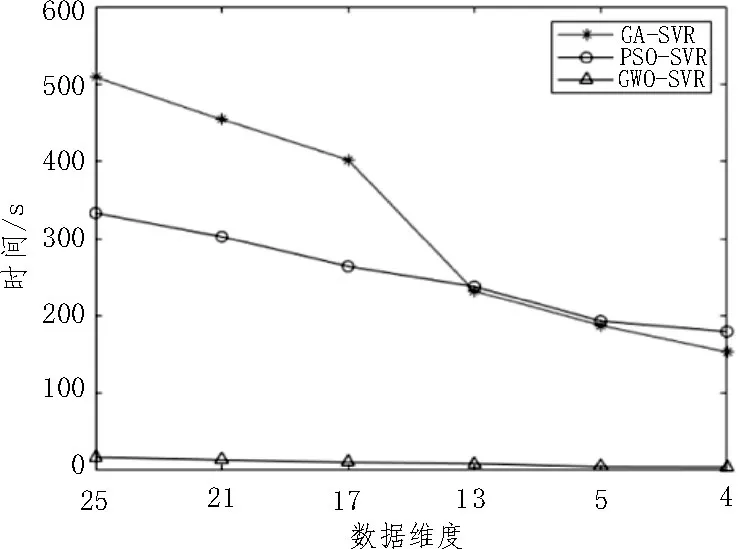
圖5 不同算法預測時間比較

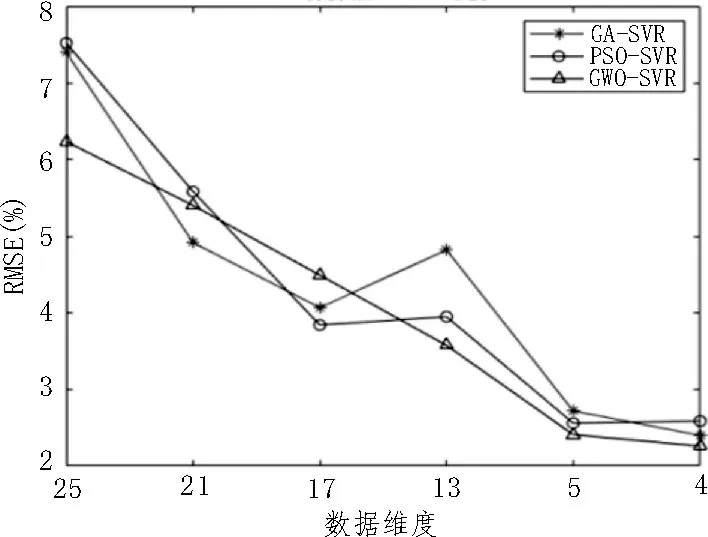
圖6 不同算法RMSE比較

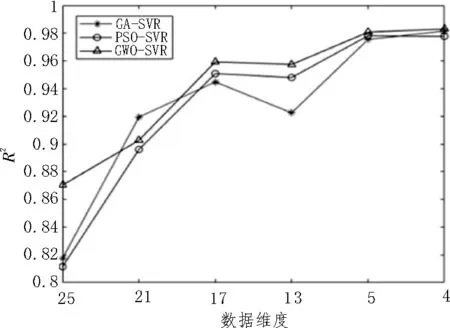
圖7 不同算法R2 比較

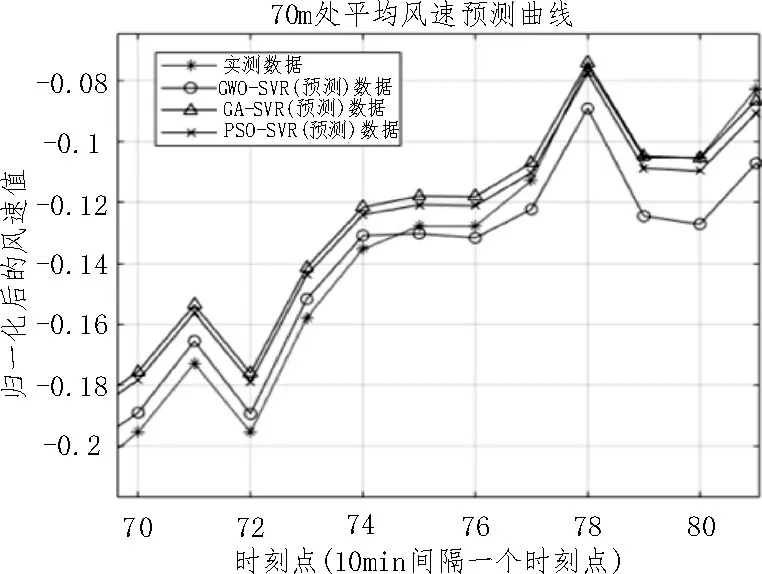
圖8 風速預測比較曲線（局部）

從圖5 可以看出，數據維度較高時（1 440×17 以上），GA-SVR 的預測時間接近PSO-SVR 的1.5 倍，在低維（1 440×13 以下）時兩者的預測時間相當，GWO-SVR 的是三種算法預測時間最短的，在高維時為PSO-SVR 的5%左右，在低維時為PSO-SVR 的2.5%左右。

從圖6 可以看出，三種算法的均方根誤差(RMSE)隨著數據維度的減少都在減小，但是在高低維過渡時GA-SVR 和PSO-SVR 算法的RMSE 存在波動，而GWO-SVR 算法為單調遞減。

從圖7 可以看出，三種算法的R2在高低維過渡時均有波動，但是GWO-SVR 算法的波動最小，并且其擬合度在低維時是三者中最好的。

通過上述比較分析可以可出，經過降維處理后GWO-SVR 預測算法在穩定性、速度及精度三個方面均有提高。

5 結論

為了更加合理地利用風電，減少風電并網對電網調峰、調頻和安全穩定運行的影響，文中在深入分析影響風機出力的主要環境因素的基礎上，以新疆某風電場為例，對其測風塔采集的高維環境監測歷史數據進行了降維處理，并在此基礎上采用GWOSVR 預測模型對該風電場的風速數據進行了預測分析，并和GA-SVR、PSO-SVR 算法進行了比較。實驗結果表明，經過降維處理后，GWO-SVR 預測算法在穩定性、速度及精度三個方面均表現了優異的性能。