河流表面圖像小波閾值去噪方法研究

袁志雄，趙東雪，張志剛，唐立軍

（長沙理工大學物理與電子科學學院，湖南長沙 410114）

河流表面圖像處理是河流流速測量的關鍵技術[1-2]，該技術通過航拍得到河流表面圖像后，再對圖像進行分析就能得到河流流速情況。由于航拍圖像在形成、傳輸和存儲過程中環境、成像設備、人為因素等影響，傳回地面的圖像嚴重受噪聲干擾。因此，降低噪聲對流速分析的干擾，對實現高性能圖象測流至關重要。

傳統的圖像去噪方法包括均值濾波法[3]和中值濾波法[4]。目前研究最為廣泛的去噪方法是小波閾值去噪[5-7]，該方法通過改變閾值和閾值函數實現圖像去噪。目前閾值函數的研究在選定一個統一閾值[8-9]或Birge-Massart 閾值[10-11]的基礎上開展：一種方法是結合中值濾波和小波變換實現圖像平滑去噪[12]；另一種方法是利用小波變換構造新的閾值函數[13-15]。文獻[16]提出一種新的閾值函數，圖像去噪效果得到提升，但因為沒有調節因子，函數的靈活性與連續性相對較差。

文中針對河流表面圖像的特點，在已有閾值函數基礎上，研究改進閾值函數連續性和靈活性，為提高河流表面圖像質量提供一種有效的參考方法。

1 河流表面圖像分析

影響河流表面圖像質量的主要因素有：①由于光線分布差異導致河流表面圖像的背景灰度分布不均勻；②水中存在大量的懸浮物，對光的吸收、散射等因素導致圖像細節模糊、信噪比較低；③風力、光照等因素變化導致回傳圖像陰影，導致圖像對比度較低。

河流表面圖像的噪聲類型主要有高斯噪聲和脈沖噪聲兩種。脈沖噪聲(又稱為椒鹽噪聲，Impulse Noise)，主要在圖像傳輸的過程中生成；高斯噪聲是一種概率密度函數呈正態分布的噪聲，又被稱為正態噪聲。由于高斯噪聲有很多種途徑可以產生，因此實際采集到的圖片在采集過程中都會有高斯噪聲摻雜。

2 河流表面圖像小波去噪

2.1 一般小波去噪方法介紹

在選定恰當的小波基后，通過使用小波變化，對含有噪聲的圖片進行多重分解，在小波系數中得到不同頻率的信號分量。結合閾值函數和準則，對其中的高頻系數分量進行閾值化處理，保留可用的有效低頻信號系數，再把兩者進行重構，得到新的去噪圖像。這種方法使圖像中的有效信號集中在系數大的小波系數中，而噪聲的小波系數是隨機分布的，利用閾值就能輕易實現去噪。小波閾值去噪流程圖如圖1 所示。

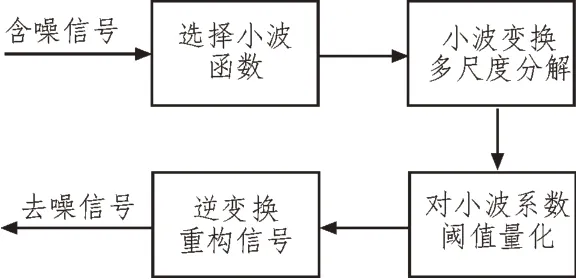
圖1 小波閾值去噪流程圖

通過分析可以得知，小波閾值去噪所需時間很短，并且適用于多種類型的圖像處理。但是不同閾值函數因為計算以及處理方法的不同，在進行小波變換時，對圖片的去噪效果會不同。經典的軟閾值和硬閾值進行去噪時由于不連續的問題容易導致圖像失真。

硬、軟閾值函數分別如式（1）、式（2）所示：

式中，Snk表示閾值處理后的估計小波系數；T表示閾值；sk表示原始含噪圖像經過小波變換獲得的小波系數。雖然硬閾值函數能解決| |Snk-sk恒定差問題，但在閾值±T處不連續，導致去噪后圖像出現視覺失真現象。軟閾值函數雖然解決了在±T處不連續的問題，但估計小波系數和真實小波系數間存在一個恒定偏差，導致圖像邊緣局部信息丟失。

2.2 閾值函數連續性和靈活性改進

在文獻[17]中，一種基于軟硬閾值函數的改善連續性的閾值函數被提出，如式（3）所示：

對式（3），當閾值趨向T+和T-時，Snk變化分別如式（4）和（5）所示：

首先，從兩個公式可以看出，文獻[17]閾值函數在閾值趨向T+和T-時，受sk和T的影響，在閾值處出現不連續的情況，再去噪容易造成圖像信息的缺失，其次，因為河流表面圖像含有復雜的噪聲，式（3）不能隨著噪聲的大小而調整去噪的手段。

因此構建如式（6）的新閾值函數：

由式（6）可得：

式中，T+表示正向無限接近于閾值T的值。從式（7）可以看出，由于，因此可以得到。同理=0，T-表示反向無限接近于閾值T的值，如式（7）和式（8）所示。閾值函數在±T處連續。閾值函數的連續確保河流圖像信號在分解后能完全重構小波系數的能量分布，不會造成去噪后重構的圖像關鍵信息缺失。

從式（9）、式（10）可以看出，當sk→∞時，改進的新函數以Snk=(1-m)sk作為漸近線，從式(11)可以看出，當sk→∞時，Snk→sk，即恒定偏差Snk-sk=0，即新閾值函數很好地克服了傳統閾值函數存在恒定偏差的缺陷，解決了傳統閾值函數去噪后的信號方差過大的問題。

文中提出的新閾值函數設置了p和N兩個調節因子，在閾值函數中發揮各自的作用，共同決定閾值函數處理過程和結果。當參數p=0，N→∞時，改進的函數就是軟閾值函數；當p→∞，N→∞時，改進的函數就是硬閾值函數。因此，文中改進的閾值函數可以調節兩個參數值的大小使閾值函數適用于不同的圖像去噪情況。在提出的改進函數中，參數p能夠調整對小波系數的壓縮程度，從而補足傳統函數的缺點。

2.3 河流圖像質量評價標準及小波閾值選擇

在河流表面圖像處理過程中，新閾值函數的小波基選擇對稱性好的sym8 小波支撐長度為6。

對于去噪函數，通常使用峰值信噪比(PSNR)來評價，如式（12）所示，其單位為dB。

閾值是小波閾值去噪的另一個關鍵因素，閾值過小會保留更多的小波系數，同時噪聲也會被保留：如果閾值太大，那么圖像中的一些關鍵圖像特征也可能會被處理掉從而使圖像信息丟失。選取含噪河流圖像根據式（12）進行仿真，比較統一閾值法和Birge-Massart 閾值法的PSNR 如表1 所示。從表1 可知，河流圖像去噪的新閾值函數選擇統一閾值法比較適宜，由式（13）可以得到新閾值函數的閾值。

表1 兩種閾值法的PSNR比較

其中，σ是噪聲δ的標準差，N表示樣本集的大小，即小波分解層的數量。

3 實驗測試與結果分析

3.1 河流圖像去噪流程

選擇Mexihat小波基并確定小波分解的層數為4。通過對含噪圖片使用離散小波變換，得到小波分解系數。由式（13）可得5 個閾值，第一層低頻的閾值即為第二層的高頻所設的閾值，所以分解為4 層，5個閾值大小順序為T0＞T1＞T2＞T3＞T4；由式（8）和式（13）分別求第一、第二、第三、第四層小波系數Snk和閾值T，從而得到新的小波系數Snk。再對這些小波系數進行逆變換,就可以得出去噪后的重構圖像。

3.2 河流表面圖像去噪實驗方案

文中實驗對象是在航拍的原始圖像中添加方差為0.01 的高斯噪聲和噪聲密度為0.01 的椒鹽噪聲形成含噪圖像，將其與經典的硬閾值函數、軟閾值函數、均值濾波、中值濾波以及文獻[17]提出的閾值函數進行仿真測試對比分析，得到各閾值函數對河流圖像去噪處理的峰值信噪比，如圖2 所示。選取噪聲標準差為σ=10，調節因子p=1、N=3，對拍攝的河流流速圖片進行小波閾值去噪處理實驗。

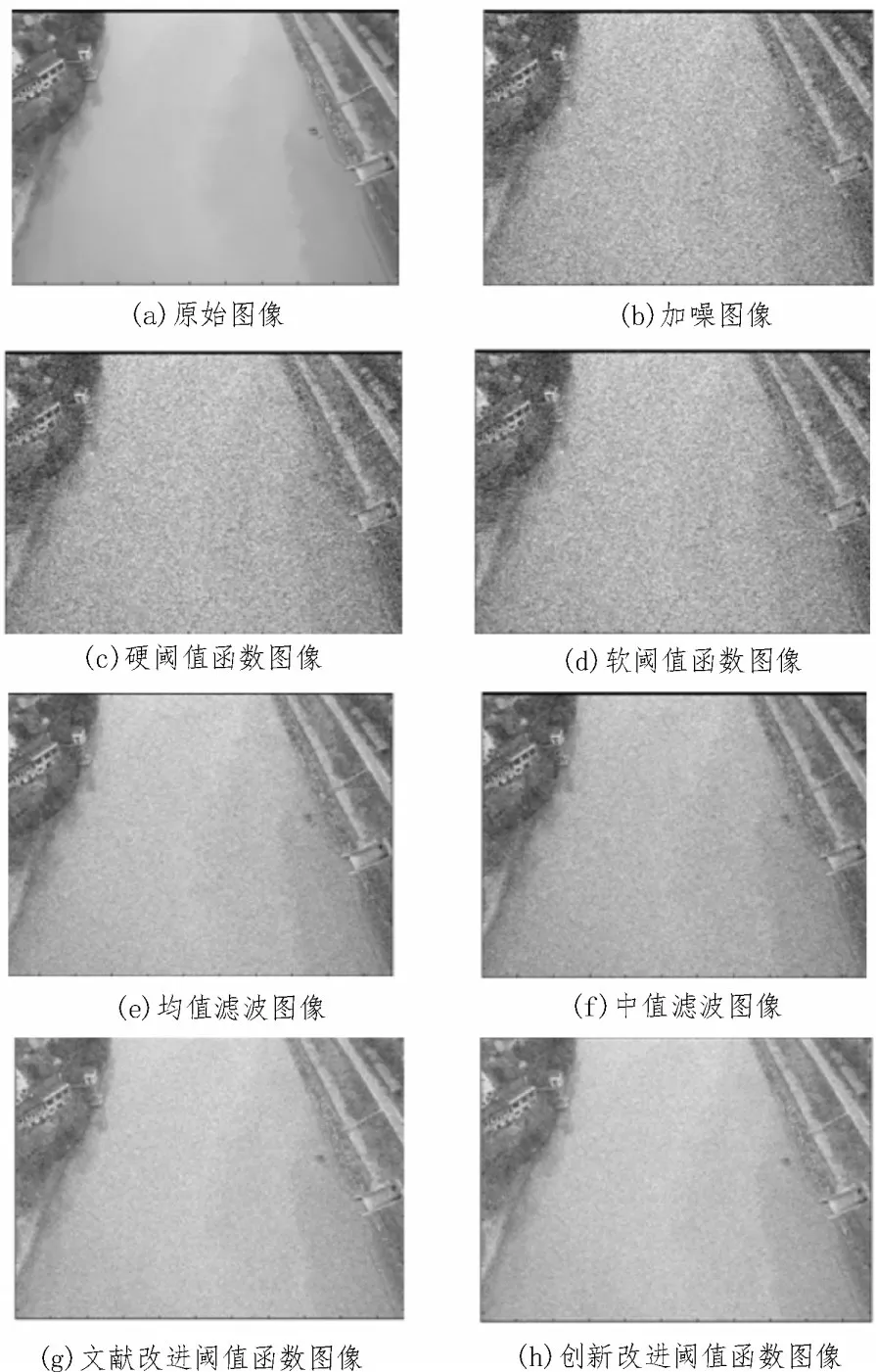
圖2 靜態河流圖像的去噪對比

從圖2 可以得知，與經典的硬閾值函數、軟閾值函數、均值濾波、中值濾波以及文獻[17]提出的閾值函數相比，在圖像的視覺改善效果上，文中所提出的閾值函數要更加清晰，圖像的細節點更多，通過閾值函數處理后的圖像計算PSNR 得到的數值也更大。

圖3 是在不同水流速度下航拍原始圖像。水流速度越快，圖像包含的信息也越多，對圖像的清晰度以及去噪恢復的影響也越大。

圖3 不同流速下航拍原始圖像

表2 顯示了當σ變大時各類去噪函數對不同流速下的圖像進行去噪后得到的PSNR。從表中可知，隨著σ變大，各類去噪函數對圖片的去噪效果和圖片的重建性能會逐漸降低。在噪聲比較大的情況下,文獻[17]提出的函數和文中改進的函數得到的PSNR相差比較小，但都比經典函數得到的PSNR 要大；在噪聲比較小的情況下，文中改進的函數的去噪效果會更好，PSNR 值會相對更高。

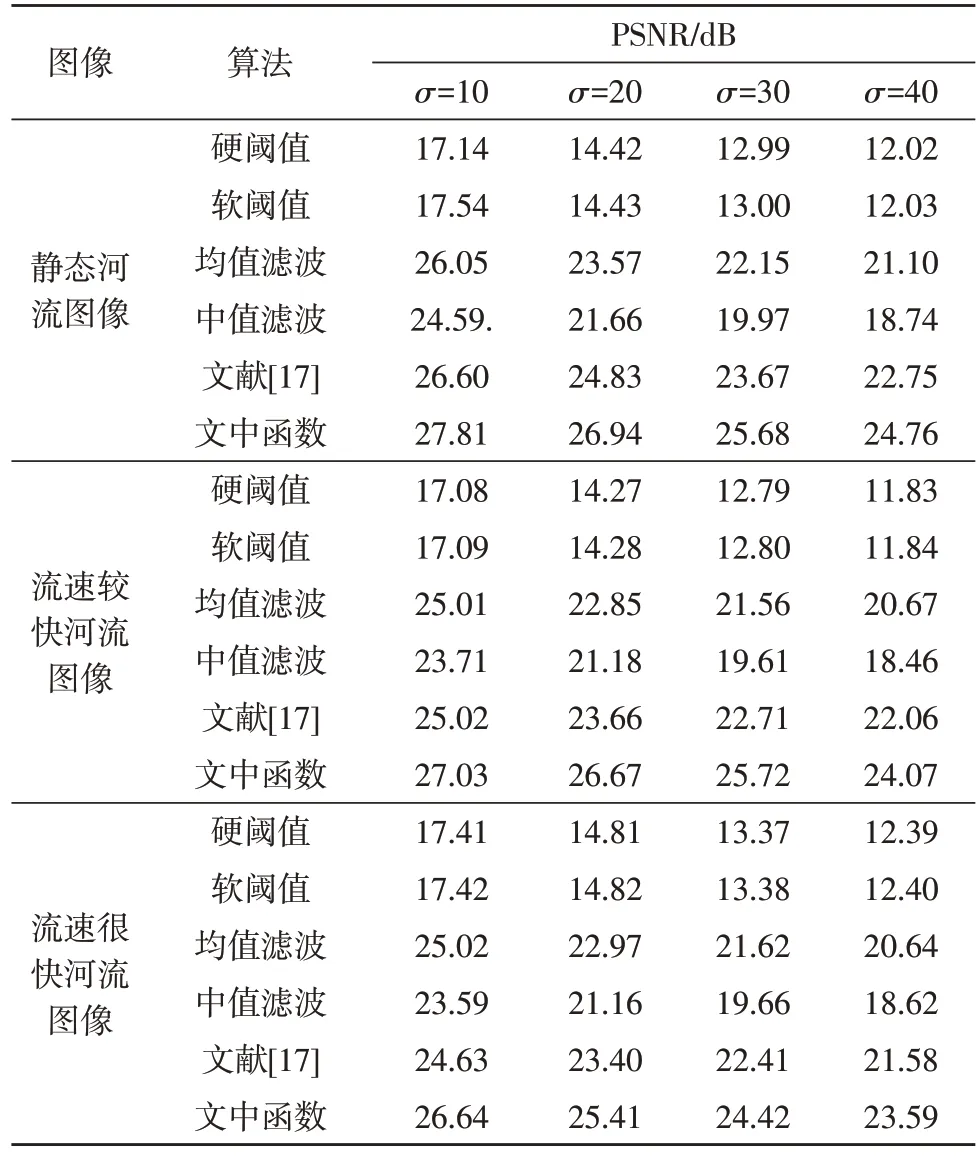
表2 各類去噪函數獲得的PSNR

設定噪聲標準差σ值為10，通過調節p和N兩個參數的值，對圖像2 進行去噪，分析不同參數值之下新閾值函數的去噪效果，得到的PSNR 如表3 所示。從表中可以看出，p和N的大小會影響新閾值函數的去噪精度。因此，在圖像去噪和重建的過程中,需要選擇適當的數值以保證較好的去噪性能。

表3 不同p和N得到的PSNR

4 結論

文中介紹了小波閾值去噪的原理，對比和分析了不同閾值函數及其特征，建立了一種去噪效果更好的閾值函數，實現了閾值的連續，而且通過設置調節因子，提高了復雜圖像噪聲條件下閾值函數的靈活性。通過對航拍河流圖像的去噪測試，相比傳統的閾值函數，文中改進的閾值函數去噪效果要更好。