直流電暈放電特性分析

鄒岸新, 王守剛, 楊滔, 劉巖, 李永明

(1.國網重慶市電力公司超高壓分公司, 重慶 400039;2.輸配電裝備及系統安全與新技術國家重點實驗室(重慶大學), 重慶 400044)

高壓直流輸電技術是中國重點發展方向之一,能夠將作為社會經濟發展重要支撐的電力資源進行優化配置。隨著電壓等級不斷提高,輸送容量不斷擴大,使得特高壓直流輸電技術不斷發展[1-2]。但當高壓直流輸電線路的電壓加到一定等級并且超過空氣的擊穿強度時,將會使空氣中的氣體電離,會使導線表面發生電暈放電現象[3-4]。電暈放電產生的電荷受空間電場的影響做漂移擴散的運動,最終產生的附加場會直接影響空間電場的分布[5]。并且電荷在空間中與運動還會產生電暈電流[5-6],直接決定了由電暈放電引起的電暈損耗,并且在放電過程中產生的聲干擾、無線電干擾、絕緣劣化等電磁環境污染問題以及電暈放電造成的腐蝕設備表面和縮短設備使用壽命問題日漸受到重視[7-9],因此開展電暈放電圍觀物理過程研究對于探究電暈放電的特征規律、指導輸電線路離子流場計算具有重要理論價值。

對于電暈放電的放電機理以及形成的離子流的相關特性,國內外學者建立不同的理論模型并進行大量的理論試驗研究,分析放電機理以及電暈放電后產生的各種電磁影響。文獻[10]提出一種考慮導線表面電場不均勻性對電暈放電影響的方法,研究超高壓交流輸電線路電暈放電對地面電場的影響。文獻[11]通過懸空導線電位補償法進行測量電暈放電產生的空間電荷的單位分布。文獻[12]建立基于泊松方程和流體動力學方程的負電暈放電仿真模型,定量研究負電暈放電中的微觀物理過程,并研究不同位置的顆粒物的運動特性。文獻[13]建立Navier-Stokes方程耦合的二維單極離子漂移模型,研究導線電暈放電時電壓和導線直徑對離子風場分布和流速大小的影響。Javandel等[14]建立漂移擴散模型來模擬正負電壓下的電暈放電差異性。 Font等[15]使用室內電暈籠和各種導體配置對高壓直流輸電線路的直流電暈特性進行了實驗和模擬研究,以指導土耳其擬建高壓直流輸電線路的設計。Fahmi等[16]采用3種漂移擴散模型和泊松方程,用有限元方法求解了負電暈放電現象,研究帶電物質的空間分布、電場分布和電離率。

電暈放電微觀過程中會產生大量的激發態粒子、帶電粒子等,空間難度大,特別是對于分子氣體放電,動理學規律極其復雜。由于缺乏有效的等離子體診斷手段,電暈放電的很多微觀參數通過試驗獲取還是有一定難度,并且應用數值計算方法分析效率不高。電暈放電屬于非平衡放電中低溫等離子體范疇,其微觀物理過程是一個典型的多物理場耦合過程。

為此,建立完全自洽的等離子體模型和簡化的電暈放電模型,研究考慮±30 kV的直流電暈放電情況。結合域方程的推導,描述載流子在傳輸區域中的傳輸,計算電暈放電產生的空間電荷密度和電勢。

1 等離子體模型

1.1 等離子體建模

等離子體通常被稱為物質的第四態,即帶電粒子、中性粒子和電磁場的導電性組合體,呈現出高度激發的不穩定態。建立等離子體仿真模型,如圖1所示,求解漂移擴散近似電子和離子連續性及動量方程,與泊松方程自洽耦合。

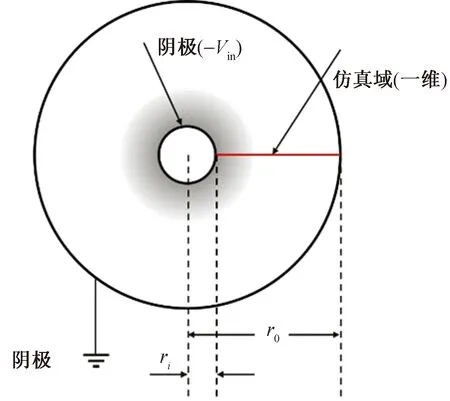
圖1 同軸構型的非等比例橫截面Fig.1 Non-equivalent cross-section of the coaxial configuration

圖1顯示了以負極為例的仿真模型幾何結構的橫截面,內部電極半徑ri為100 μm,電極之間的間隙r0-ri為10 cm,陰影區域表示由陰極附近產生的正空間電荷分布產生的電離區域。假設觀點在徑向上均勻擴散,所以可以簡化為在電極之間的徑向方向上是以為的。假設其體溫度和空氣數密度是恒定的。其中采用“局部場近似”,這意味著假設傳遞系數和源系數通過約化電場 (E/N) 進行適當的參數化。并且也不涉及求解平均電子能的流體方程,因此,數值問題求解的復雜性可以大幅度降低,提高計算效率。

“局部場近似”有效的條件是,電子從電場中獲得能量的速率與能量損耗率局部平衡。當滿足這一條件時,電子平均屬性可以表示為約化電場的函數[17],此時電子與電場是處于局部平衡狀態的。

使用圖1所示的模型模擬在內導體上施加電勢時惰性氣體的電離以及帶電顆粒的傳輸。高電勢和較小的導體曲率半徑共同產生的強電場會導致電暈絲周圍的惰性氣體電離。

1.2 域方程

先求解電子密度的漂移擴散方程來計算電子密度,避免因為使用電暈放電接口的強近似而只求解離子傳輸問題。求解公式為

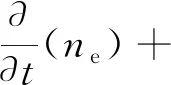
(1)

式(1)中:ne為電子密度;μe為電子遷移率;E為電場強度;De為電子擴散系數;Re為離子復合項。

應用“局部場近似”時,傳輸系數和源系數直接通過約化電場來直接映射,電子密度方程不再求解。實際上,當使用局部場近似或局部能量近似時,傳輸系數和源系數仍以平均電子能的函數形式給出[18]。但使用“局部場近似”時有所不同,此時必須提供一個能將平均電子能與約化電場聯系起來的函數,而使用“局部能量近似”則不需要。平均電子能的計算公式為

ε=F(E/N)

(2)

式(2)中:N為氣體粒子數密度。

根據電子遷移率計算出電子擴散系數,表達式為

De=μeTe

(3)

式(3)中:Te為電子溫度。

等離子體化學成分的速率系數決定了源系數。對于速率系數的求解,電子源項表達式為

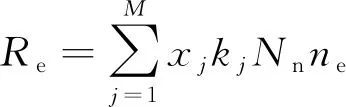
(4)

式(4)中:xj為反應j的目標物質的摩爾分數;kj為反應j的速率系數,m3/s;Nn為總中性數密度,m-3。

對于直流放電,使用湯森系數而不是速率系數來定義反應速率。此時,電子源計算式為

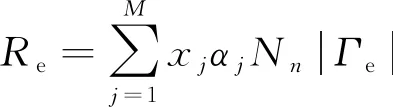
(5)

式(5)中:αj為反應j的湯森系數,m2;Γe為電子通量,m2/s。當電子通量像直流放電一樣被場驅動時,湯森系數可以提高數值方案的穩定性[19-20]。

對于非電子物質,對每種物質的質量分數求解以下方程,即

(6)

式(6)中:ρ為混合物的密度,kg/m3;wk為第k種物質的質量分數;u為質量平均流體速度矢量,m/s;jk為擴散通量矢量;Rk為第k種物質的速率表達式,kg/(m3·s)。

靜電場的計算方程為

-?·ε0εr?V=ρ

(7)

式(7)中:ε0為真空介電常數;εr為相對介電常數;V為電勢,空間電荷密度ρ根據模型中指定的等離子體化學成分自動計算,公式為

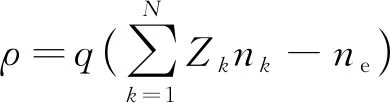
(8)

式(8)中:Zk為第k種物質的電荷量;nk為第k種物質的密度。

2 簡化的電暈模型

用等離子體自洽模型需要非常小的時步來描述其物理場,對于電暈放電進行建模的計算量非常大。原因之一是可能會發展出電離波,增加了問題的數值難度,并增加了計算時間。高維模型對工業應用而言不太現實,因此采用簡化模型。

簡化模型使用與圖1所示的等離子體模型相同的幾何結構,滿足基于帶電載流子傳輸的電流守恒,由于需要在電暈電極上同時給出電勢和電場,因此模型不是自洽的,即維持放電所需的電場不是根據第一原理獲得的,電子和離子傳輸、電子從電場中獲取能量,電子在于背景氣體碰撞時損失能量。

在穩態下的電暈放電中,背景氣體的電離發生在離電暈電極非常近的區域,即所謂的電離區。在電離區和大電極 (通常接地)之間,只有一種載流子:正離子或負離子,具體取決于電暈的極性。該區域稱為傳輸區域。對于某些涉及電暈放電的應用,不需要用到等離子體模型的所有復雜方面,可以使用簡化的模型來獲得空間電荷密度和電勢。

使用簡化的模型來描述一種載流子在傳輸區域中的傳輸。維持放電的等離子體物理場濃縮在電暈電極的給定電場區域。顯然,電暈電極上提供的電場的大小對于獲得電勢和空間電荷密度的精確值是至關重要的。

2.1 域方程

根據電荷守恒方程和泊松方程,建立簡化的電暈模型,以此來求解載流子在電暈放電過程中的傳輸問題。當僅包括電場漂移時,域方程為

?·J=S

(9)

J=zμρE

(10)

ε0?2V=-ρ

(11)

式中:J為電流密度,A/m2;S為電流源,A/m3;z為電荷數;μ為遷移率,m2/(V·s);ρ為空間電荷密度,C/m3;E為電場;V為電勢;ε0為真空介電常數,獲得輸運方程,即

(12)

假設遷移率是恒定的。在沒有源項的情況下,該方程廣泛應用于模擬靜電除塵器中的空間電荷密度的假設格式,即

(13)

在簡化形式下,方程不依賴于載流子的任何屬性,正負電暈中V和ρ的解是對稱的。與等離子體產生分布和維持放電相關的信息,都體現在內電極的邊界條件設置里,在這里求解的域方程中沒有涉及。

2.2 邊界條件

電暈電極上電場的法向分量用作泊松方程的邊界條件,表達式為

n·E=E0

(14)

泊松方程的另一個邊界條件是外電極處的V=0。邊界條件涉及采用拉格朗日乘子[21]求得電暈電極上的空間電荷密度ρq,從而驗證施加的電勢V0。 表達式為

V-V0=0

(15)

在簡化模型中,設置在電暈電極上施加電勢和電場。為了獲得和等離子體模型一致的預測的物理結果,應用匹克定律求解起始電暈電場,保證導線處的場強嚴格接近真實的數值。匹克定律為

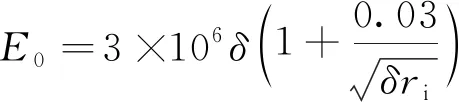
(16)

式(16)中:E0為擊穿電場,V/m;δ為氣體數密度;ri為電暈電極的半徑。

3 仿真結果

3.1 負電暈放電微觀過程

根據圖1建立的模型,負電位(-Vin)施加在內部導體(陰極)上,外電極接地(陽極),分析負極導線周圍的空間電荷分布情況。呈現和討論的所有結果都對應于穩態操作。在內電極上施加-30 kV時的直流負電暈,獲得負電暈的帶電物質數密度如圖2所示(為更清晰地展示粒子密度在截面上的分布情況,將計算結果取對數進行數學處理)。

圖2 負電暈帶電物質數密度的二維表示Fig.2 Two-dimensional representation of number density of charged matter in neqative corona

圖2是帶電物質數密度通過一維解獲得的二維表示。在電暈放電中涉及各種各樣的電離反應,其中最主要的是電子和空氣中中性分子碰撞電離。為了深入探求電暈放電的微觀機理,需要對電子密度的分布進行分析計算,因為在外加電場和重粒子之間,電子是能量傳遞的主要載體。電子在向陽極運動的過程中,會不斷和空氣中的物質發生碰撞和電離,朝向陽極的基本電子崩也隨之建立,同時激勵反應和電離反應也在伴隨產生。因此從陰極到陽極,電子的分布區域逐漸擴充,這一點從圖2中可以明顯看出。電極的大部分體積被在陽極方向上漂移的負離子填充。

圖3～圖5顯示了電子溫度、電勢和約化電場的結果。可以看出,在到達電極的部分區域具有弱電場,因而具有電子溫度。在該區域中,電子沒有足夠的能量發生電離并有效的附著形成負離子。因此,放電的一個較長的空間部分向接地電極漂移的負離子控制。另外,在此區域中,電荷分離幾乎不會使外加電勢的分布發生形變。

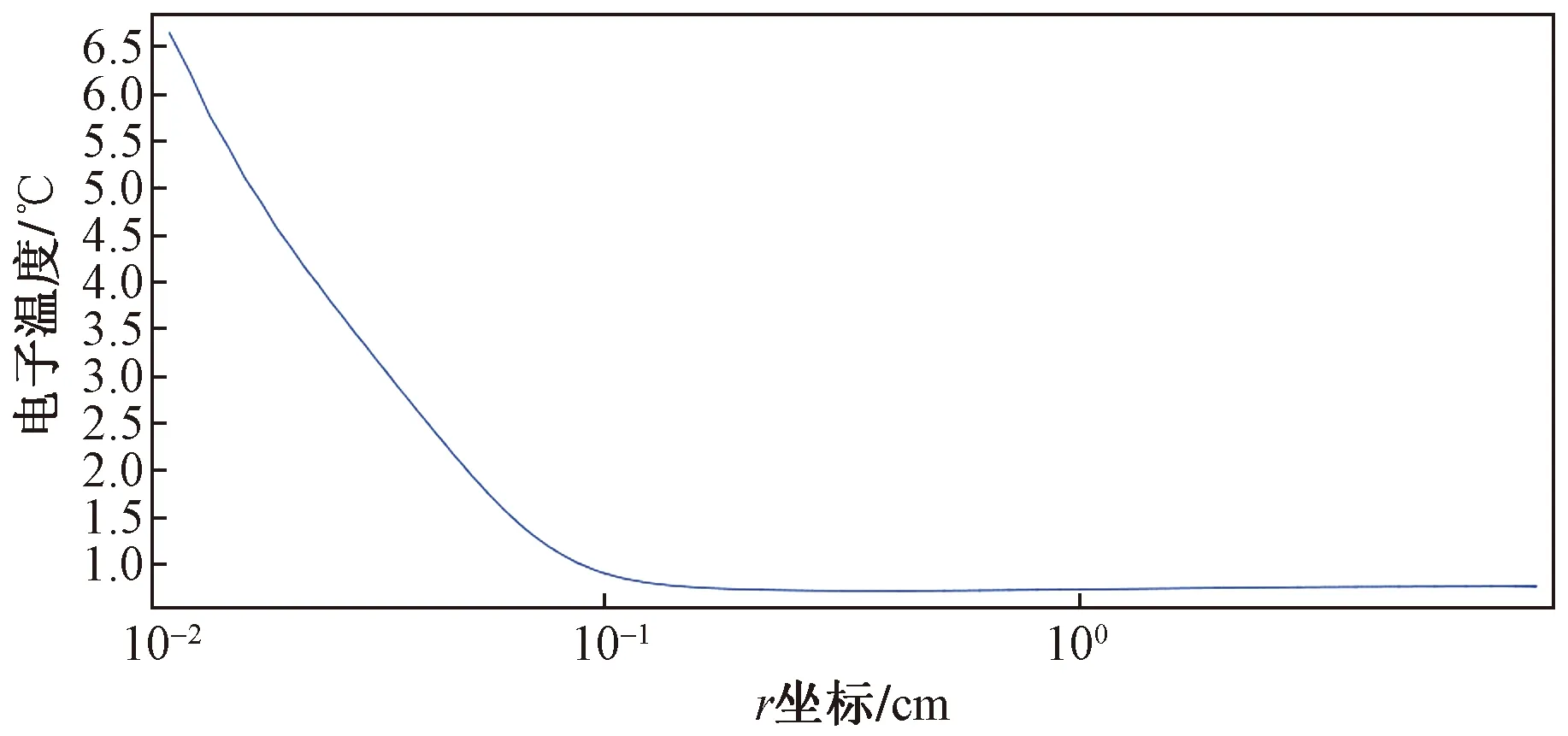
圖3 電子溫度的空間分布Fig.3 Spatial distribution of electron temperature

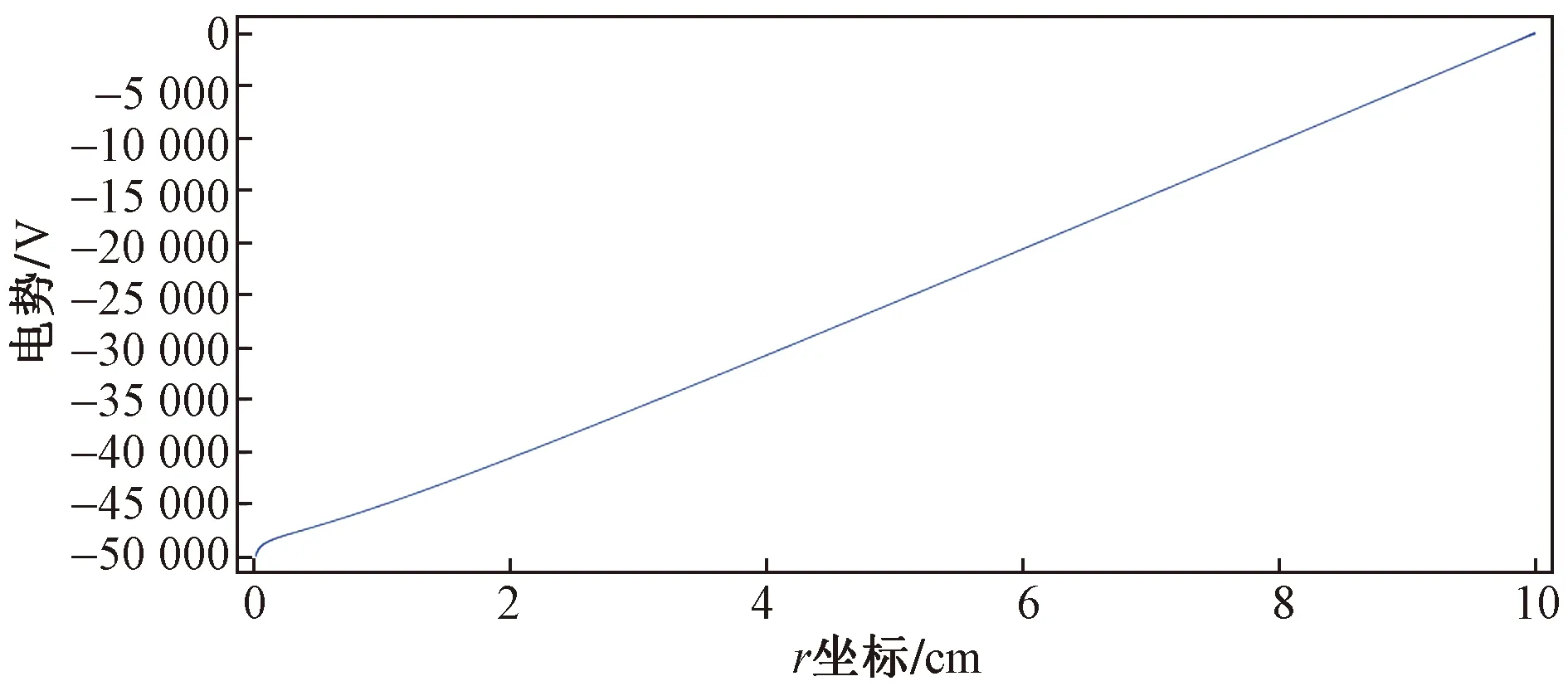
圖4 電勢的空間分布Fig.4 Spatial distribution of electric potential

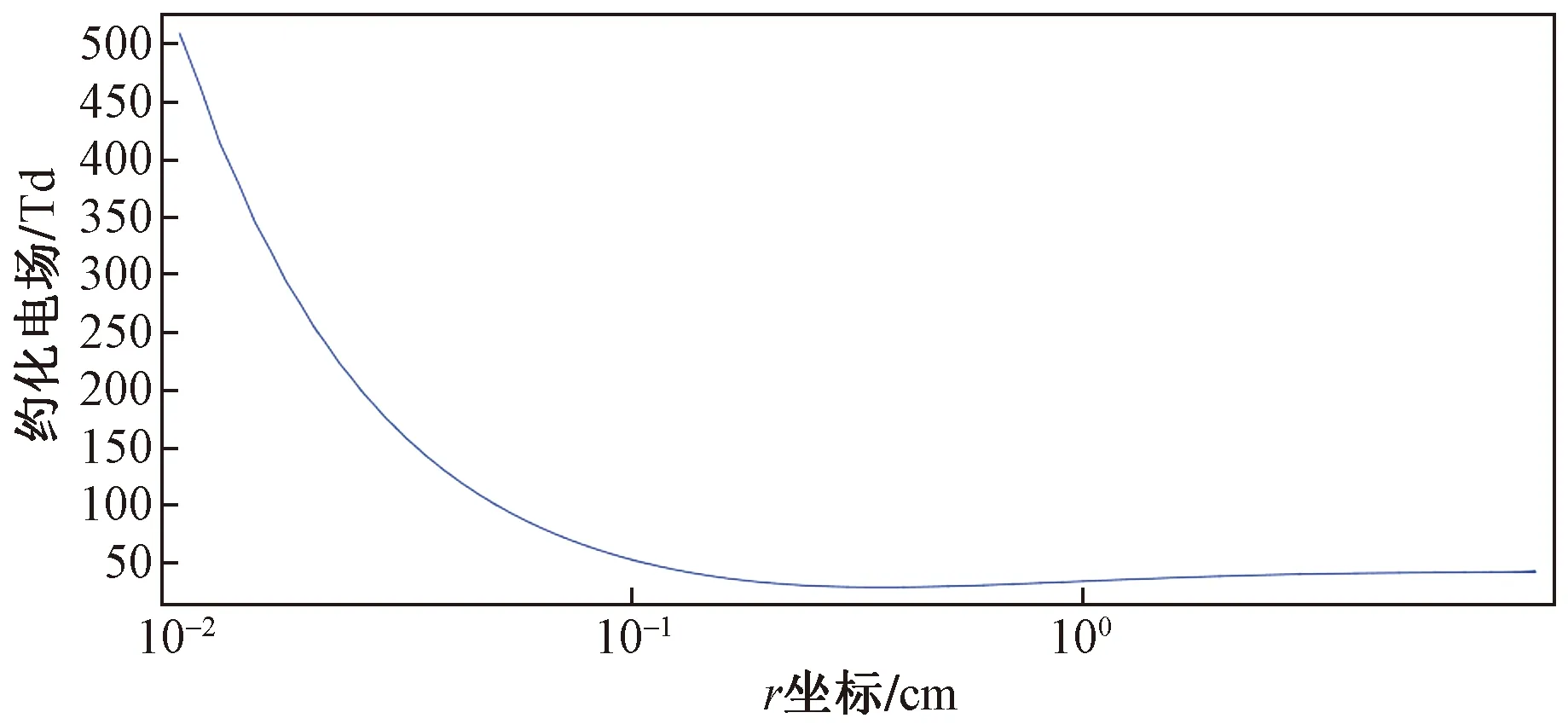
圖5 約化電場的空間分布Fig.5 Spatial distribution of thereduced electric fields

圖6顯示了接地電極出總離子流的絕對值與內電極處外加電壓的絕對值的函數關系。電流-電壓特性遵循預期的二次定律。所獲得的電流密度值也與這種放電的值一致。

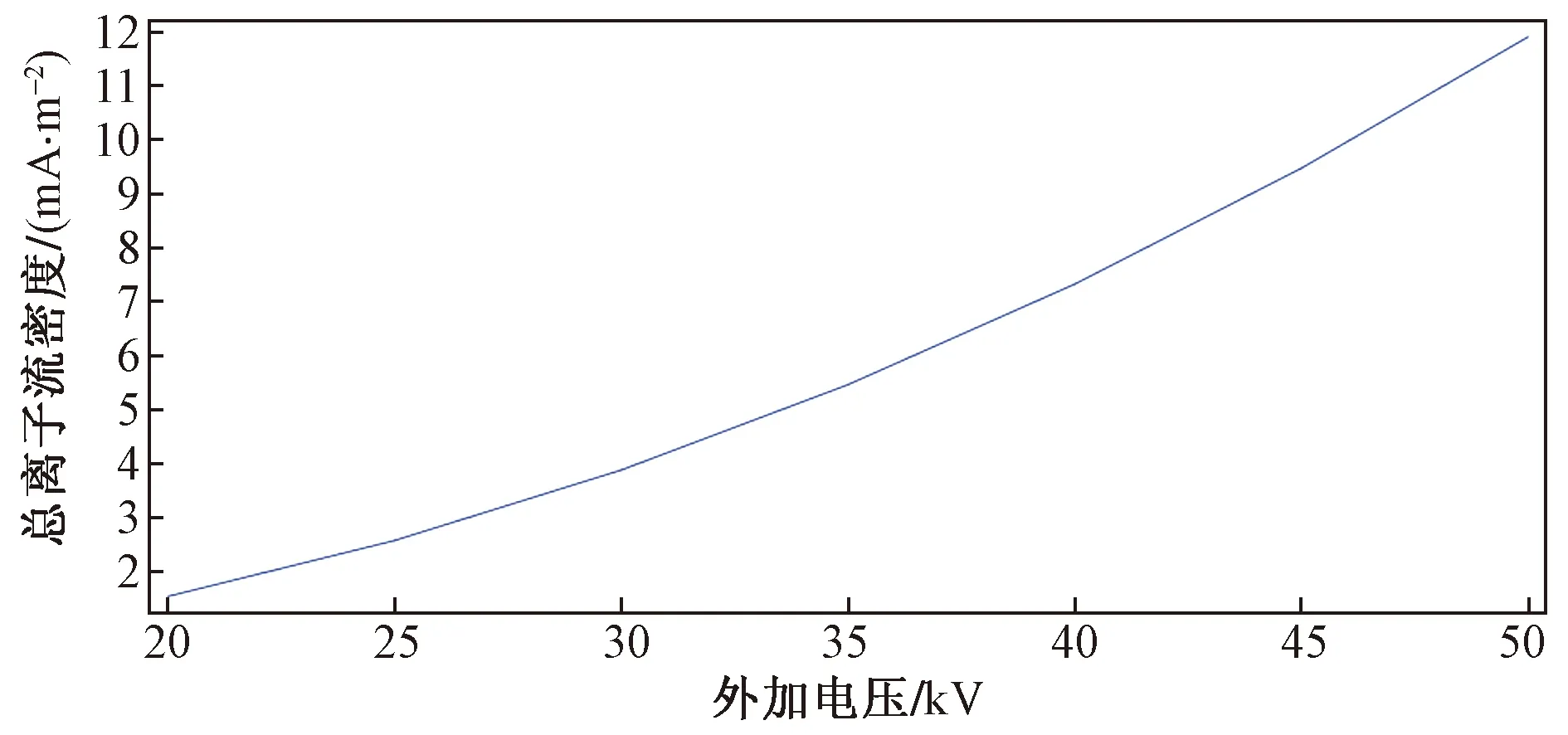
圖6 接地電極總離子流密度與外加電壓的函數關系Fig.6 Function of total ion current density of grounded electrode and applied voltage

3.2 自洽的等離子體模型

空氣中等離子體的化學性質非常復雜,對主要激發態的詳細研究很容易產生數百種反應。但在研究過程中主要關注的是電荷粒子密度的分布以及產生的電流情況。因此,在建模中可以使用一組簡化的反應來替代,描述干空氣背景下帶電物質的產生和消失。具體計算結果如圖7所示。

圖7 電暈帶電物質的數密度Fig.7 The number density of charged matter in corona

圖7顯示了用等離子體模型獲得的正負電暈的帶電物質的空間分布。從中可以看出,電暈放電在兩個區域中進行:一個是主要發生電離區,另一個是粒子傳輸區。電離區主要是發生在陰極附近1 mm以內的區域,傳輸區是到達接地電極的其余部分。兩個區域中關于粒子的分布有明顯不同。圖7(a)表示的正電暈帶電物質濃度分布中,正離子密度在所有區域中占主導地位,而在圖7(b)關于負電暈的描述中,正離子僅在陰極下降區占主導地位,而在傳輸區中,負離子占主導地位。

圖8描述了通過自洽模型獲得的各種極性的主要載流子的速率表達式:正離子用于正電暈,負離子用于負電暈。正電暈中,正離子是在電暈電極附近的狹窄區域中由基態的電子碰撞電離產生的。負電暈中,負離子是通過電離和傳輸區域中的電子附著產生的。

圖8 正電暈的正離子和負電暈的負離子速率表達式Fig.8 Expressions for the rates of positive ions and negative ions of positive corona

3.3 簡化模型與自洽的等離子體模型對比

空間電荷密度的分布是整個放電過程中帶點粒子的宏觀反映。對比兩個模型的電勢和空間電荷密度得到的結果如圖9所示。

圖9 正負電暈的電勢空間電荷密度Fig.9 Space charge density and potential of positive and negative corona

圖9顯示了通過自洽模型和簡化模型獲得的電勢和空間電荷密度的空間分布。其中在圖8中將負電暈的電勢乘以-1,以便比較曲線形狀。在正電暈的簡化模型仿真中,對電極處的電場使用了皮克定律,沒有添加源項。電勢和空間電荷密度與通過等離子體模型獲得的結果具有合理的一致性。差異主要歸因于通過Peek定律獲得的較低強度的電場。這一點在負電暈模型中得到了證明,這兩個模型的仿真結果都非常吻合。

在簡化的負電暈模型中,做了兩個重要的更改以改善模型之間的一致性:內電極上的電場是從等離子體模型獲得的電場,由于電子附著物在傳輸區域中非常重要,因此還添加了來自等離子體模型的載流子的源。

對比兩個模型獲得的電勢和空間電荷密度結果:與稀有氣體中的電暈放電相比,空氣電暈放電需要更高的電壓來擊穿背景氣體并維持放電。造成這種情況的主要原因有兩個。首先是空氣中的電子碰撞頻率較高,其中部分是由于旋轉和振動相互作用所致,使得電子加速更加困難,其次是空氣中的氧帶負電。

從上述結果可以看出,通過簡化模型獲得的空間電荷密度和電勢與通過自洽等離子體模型獲得的仿真結果非常吻合。

4 結論

為研究電暈放電的微觀物理過程,建立自洽的等離子體模型和簡化的電暈放電模型,定量描述了電暈放電的微觀特征的情況,其中以負極為例,重點分析負極空間物質數密度的情況。最后對兩個模型獲得的電勢和空間電荷密度進行比較和討論。

研究結果表明,正負電暈放電特征各不相同。只要電暈電極處的電場和載流子的速率表達式足夠接近,簡化模型就可以重現用等離子體自洽模型獲得的電勢和空間電荷密度,并且二者具有很好的一致性,從而簡化計算,提高計算效率。