基于時變特性的多層腦網絡拓撲屬性分析及腦疾病分類

李濤, 邱震鈺, 李瑤, 李囡, 李埼釩, 郭浩*

(1.太原理工大學信息與計算機學院, 太原 030024; 2.南昌理工學院計算機信息工程學院, 南昌 330044;3.太原理工大學軟件學院, 太原 030024)

由于具有無創性和非侵入性的特點,功能磁共振成像技術目前已經被廣泛應用于神經精神疾病的研究中[1]。研究人員常利用靜息態功能磁共振成像技術通過血氧水平依賴信號表征腦區間自發的神經元活動,進而計算該信號的時間相關性表示腦區間的交互活動,以此構建腦功能網絡來闡明疾病的病理機制從而實現分類[2-3]。

傳統的腦網絡認為靜息態功能磁共振掃描期間功能連接是不變的[4]。但這在很大程度上忽略了大腦網絡的動態特征,而最近的研究表明大腦是一個高度動態的網絡系統[5-6]。基于此,研究人員提出了多層腦網絡,用于表示隨著掃描時間的推移腦區之間交互的時變特性[7-10]。

在已有的多層腦網絡研究中,大多集中于對動態功能連接的探索,極少從網絡的拓撲屬性角度進行分析。但拓撲屬性的引入有利于充分表征網絡的結構信息,因而對精神疾病的診斷具有重要意義。目前針對多層網絡拓撲屬性的研究分為以下幾種策略。①通過計算連接的連接將多層網絡轉變為單層網絡,從而對單層網絡的屬性進行研究[11],但該方法本質上還是對單層網絡屬性進行分析;②將單層網絡特定拓撲指標計算方法按照其特征擴展到多層網絡,而此過程不適用于所有的單層拓撲指標到多層拓撲指標的轉換,缺乏泛化性[12-13];③通過計算每層網絡中拓撲指標的均值[6]或標準差[14-15]作為多層網絡的拓撲指標值,這也是如今多層腦網絡中最常用的一種計算拓撲指標值的方法。但是簡單計算均值使得多個單層網絡拓撲指標的極值無法得到有效利用,而這些值可能在一定程度上包含大腦的動力學信息[16];同時,單純計算標準差的方法雖然可以反映多個單層網絡中拓撲指標離散的絕對程度,但又會受到所有單層網絡拓撲屬性均值的影響[17]。

為了解決以上局限性,本研究在現有的利用均值和標準差計算多層網絡拓撲屬性的基礎上,考慮到特定屬性值及整體分布的影響,分別引入極差、相對極差、離散系數進行多視角多層網絡拓撲屬性的計算,從而實現對自閉癥的分類。

首先,利用滑動窗口方法構建時變多層腦功能網絡。其次,分別基于均值、極差、相對極差、標準差、離散系數計算多層網絡的拓撲屬性,并利用Kolmogo-rov-Smirnov(KS)非參數檢驗選取差異特征。然后,使用支持向量機(support vector machine, SVM)分別基于每種方法選取的差異特征及所有差異特征構建分類模型,比較不同方法的分類效果及研究中涉及的參數對分類性能的影響。最后,利用ADNI(Alzheimer’s disease neuroimaging initiative)數據集分析方法的可拓展性。相比于現有方法,本研究所提出的方法應取得更好的分類效果且具有較好的泛化性。

1 材料和方法

1.1 方法框架

基于時變特性的多層腦網絡拓撲屬性分析及腦疾病分類主要包括以下四個步驟。其具體流程如圖1所示。

圖1 方法框架Fig.1 Method framework

(1)數據獲取和預處理。

(2)多層腦功能網絡構建。利用滑動窗口方法構建基于時變特性的多層腦功能網絡。

(3)特征提取。分別基于均值、極差、相對極差、標準差、離散系數視角計算多層網絡的度、離心率、介數中心度。

(4)特征選擇與分類。將非參數置換檢驗選取的每種視角下具有顯著差異的特征及融合所有特征作為分類器的輸入,并使用支持向量機對疾病進行分類。

1.2 數據集和預處理

1.2.1 數據獲取

樣本來源于自閉癥腦影像數據共享中心(ABIDE, http://fcon_1000.projects.nitrc.org/indi/abide)中的紐約大學朗根醫療中心。各組數據排除標準為:①女性;②頭動大于3 mm或轉動大于3°。本研究最終納入65例自閉癥患者及76例健康對照。所有數據貢獻者均通過機構審查委員會批準,且與受試者(或其監護人)簽署知情同意書。所有被試詳細信息如表1所示。其中,數據范圍指最小值～最大值(平均值±標準差),ADOS-total表示自閉癥診斷觀察量表總分,P由雙樣本雙尾T檢驗獲得。

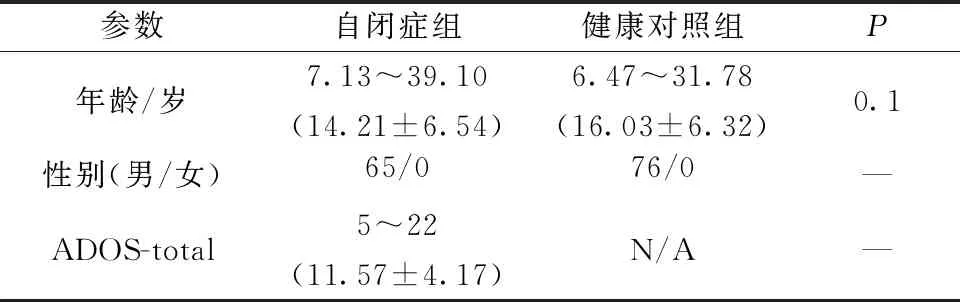
表1 被試的基本信息表

1.2.2 數據預處理

數據預處理使用GRETNA工具箱[18]進行,具體步驟包括:①去除前5個時間點數據;②時間層校正;③頭動校正;④將圖像配準至蒙特利爾神經研究所標準空間;⑤采用6 mm半高全寬的高斯濾波器對圖像進行空間平滑;⑥去除協變量,如Friston 24頭動參數、線性趨勢、全局信號、腦白質及腦脊液信號;⑦帶通濾波(0.01～0.1 Hz)。在校正過程中有3例自閉癥患者和3例健康對照因頭動大于3 mm或轉動大于3°而被舍棄,不包含在最終的141名被試中。

1.3 多層腦功能網絡構建

使用自動解剖標記模板[19]將大腦劃分為90個腦區。把每個腦區作為腦網絡中的一個節點,計算該腦區中所有體素在不同時間點上的血氧水平依賴信號的算術平均值來表示該節點的值。

采用滑動窗口方法[5, 20-21]構建時變多層腦功能網絡,通過不同窗口內的時間序列構建單層網絡,表示在一小段時間內腦區之間的功能連接,并引入層間連接表示不同層之間的腦區連通性。如圖2所示,首先,參照后續對滑動窗口參數的分析,將窗口長度設置為100 s,窗口滑動步長設置為1個重復時間(repetition time, TR)。然后,在每個時間窗內,通過計算兩兩腦區之間的皮爾遜相關系數作為腦網絡中的節點連邊的值,從而得到126個90×90的對稱矩陣。同時,為減少弱連接或虛假連接的影響,本研究采用15%的連接密度對每個窗口的連接矩陣進行閾值化。而由于負連接具有模糊的生理解釋,在網絡閾值之前將其刪除。最后,考慮到相鄰時間段上同一腦區之間的耦合,將鄰接層中同一節點之間的連接權重設置為常用值1[12-13],其余情況的層間連接值為0,從而生成時變多層腦功能網絡。

圖2 構建多層腦功能網絡Fig.2 Construct multilayer brain functional network

1.4 特征提取

利用滑動窗口方法構建時變多層腦功能網絡后,選取度、離心率、介數中心度這三個局部拓撲屬性作為特征。

1.4.1 單層網絡拓撲屬性計算

首先,對于每個滑動窗口內的功能連接矩陣,計算度、離心率、介數中心度來刻畫單層功能連接網絡的拓撲結構。

度是該節點連接到網絡中其他節點的邊的數量[16]。其計算公式為

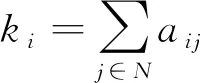
(1)

式(1)中:i、j表示節點;N表示節點數量;aij表示無向加權網絡中節點i和節點j的連接。

離心率是該節點到網絡中其他節點的所有最短路徑中的最大值[22]。其計算公式為

ei=max{d(u,v)}

(2)

式(2)中:d(u,v)指的是節點u到節點v之間最短路徑的值。

介數中心度用來衡量節點對于網絡的重要程度[11]。其計算公式為

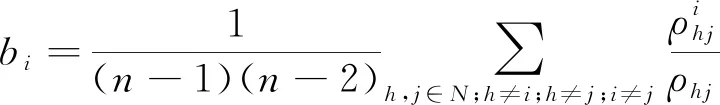
(3)

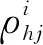
1.4.2 多層網絡拓撲屬性計算

接著,基于每個單層功能連接網絡所得到的拓撲屬性,計算時變多層網絡的拓撲屬性。傳統的分析方法中,通過計算所有單層網絡的拓撲指標的均值[6]或標準差[14-15]作為多層網絡的拓撲指標。但單純計算均值無法有效利用有代表性的特定屬性值的信息[16],而計算標準差的方法又在一定程度上受到均值的影響[17]。為解決以上問題,在已有方法的基礎上提出了從極差、相對極差、離散系數這三個視角入手計算多層網絡拓撲指標的方法。具體來說,基于極差、相對極差、離散系數視角的方法分別通過計算所有單層網絡的拓撲指標的極差、相對極差、離散系數作為多層網絡的拓撲指標。其具體的計算公式如表2所示。

表2 多層拓撲屬性計算

1.5 特征選擇與分類

雖然將多層網絡拓撲屬性作為特征可以從不同方面描述腦網絡特性,但存在冗余或不相關特征影響分類器的性能[9, 23]。因此需要對所計算的特征進行選擇,選取組間差異顯著的特征進行分類。

本研究把非參數置換檢驗[10]作為特征選擇方法,選取具有顯著組間差異的特征。具體來說,針對自閉癥患者和健康被試,分別將基于均值、極差、相對極差、標準差、離散系數的多層網絡拓撲指標計算方法所產生的270個局部屬性進行組間KS非參數置換檢驗,選取具有顯著差異的特征(P<0.05, 已校正)參與分類模型構建。同時將5種方法計算的差異特征首尾串聯構建融合特征進行分類。

深度學習已經被廣泛應用于各種疾病的診斷中[24-25],但訓練其模型需要大量被試[26]。而支持向量機適用于小樣本數據集和具有高維的特征[27-28]的腦疾病分類研究。由于本研究最終用于分析的樣本量較少,很難獲得完全的信息。因此,在對實驗被試進行分類的過程中使用支持向量機工具包(https://www.csie.ntu.edu.tw/～cjlin/libsvm/)的徑向基核函數(radial basis function, RBF)構建分類模型。

本研究利用留一交叉驗證評價分類性能。此外,為了獲得更好的分類效果,訓練集利用K折交叉驗證[29-30]對SVM參數——懲罰因子c和核函數g進行尋優。值得注意的是,構建分類模型前需對分類特征進行標準化。

2 結果

2.1 多層網絡拓撲屬性分析

為確定基于均值、極差、相對極差、標準差及離散系數計算的多層網絡拓撲結構是否存在顯著差異,本研究對這5種多層網絡拓撲屬性計算方法進行了比較,如圖3所示。

首先,針對每個被試把通過不同拓撲屬性計算方法得到的90個腦區的度、離心率、介數中心度進行平均獲得各自拓撲屬性計算方法的平均度、平均離心率、平均介數中心度。然后,分別計算自閉癥組和健康對照組基于5種拓撲屬性計算方法得到的平均度、平均離心率、平均介數中心度的均值,并用直方圖進行表示。最后,用色塊圖表示在自閉癥組和健康對照組中分別使用KS檢驗獲得的不同拓撲屬性計算方法所得到的平均度、平均離心率、平均介數中心度的統計顯著性。結果顯示,無論自閉癥組還是健康對照組,基于度、離心率及介數中心度分別使用5種統計指標計算的多層網絡拓撲屬性均存在顯著差異(P< 0.05),這表明本研究所提出的方法從不同角度刻畫了多層網絡的拓撲結構。

2.2 差異性腦區

將基于均值、極差、相對極差、標準差、離散系數計算的多層網絡拓撲屬性進行組間KS非參數置換檢驗,選取通過錯誤發現率校正后P<0.05的腦區作為自閉癥組與健康對照的顯著差異腦區,其在模板空間中的分布如圖4所示,對應的腦區名稱及其顯著性如表3所示。

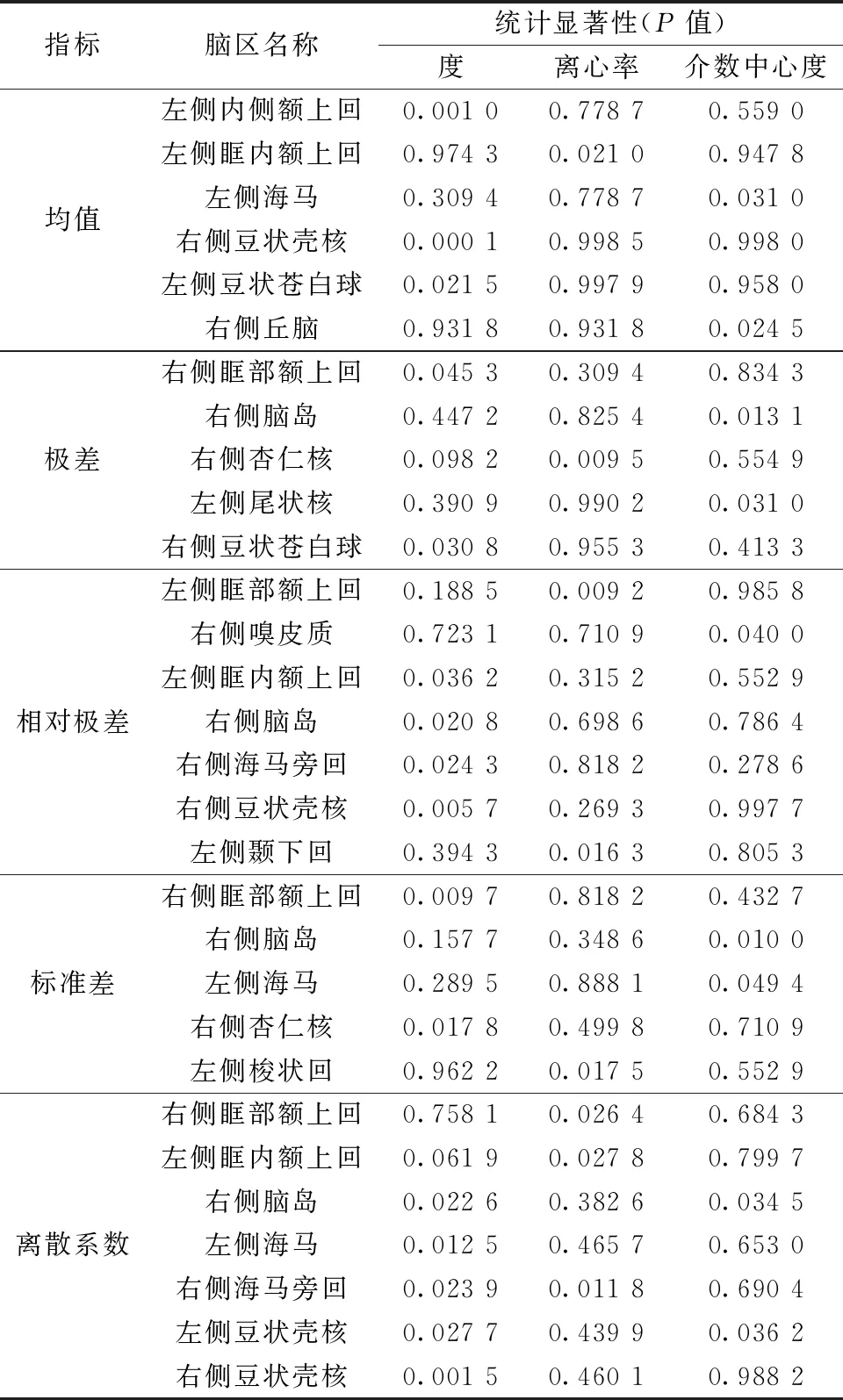
表3 節點指標異常腦區及其顯著性

圖4 差異性腦區分布圖Fig.4 Differential distribution of brain regions

結果顯示基于不同視角計算多層網絡屬性存在較少頻繁出現的組間差異腦區,主要包括右側眶部額上回、左側眶內額上回、右側腦島、左側海馬、右側豆狀殼核。這表明本研究所提出的方法可以從不同角度全面的獲得自閉癥的差異腦區。同時,這些差異腦區和目前已經被證明與自閉癥有關聯的腦區一致。Tang等[31]研究定量磁共振成像在兒童自閉癥診斷中的應用,結果顯示患有自閉癥的兒童在雙側豆狀殼核、左側尾狀核的腦血流量低于健康對照組。Liang等[32]的研究結果表明,與健康對照組相比,自閉癥患者在右側海馬旁回、左側海馬、右側眶部額上回的功能連接神經回路數量明顯減少。Duan等[33]表明自閉癥的神經影像學標志物包括右側嗅皮質、右側腦島、左側顳下回。Qin等[1]的研究發現自閉癥兒童相比于健康對照組在額上回腦區的功能連接顯著減少。Wang等[4]發現自閉癥的發展與腦島高度相關。Peng等[2]的研究發現,與健康對照組相比,自閉癥患者的雙側豆狀蒼白球在平均度屬性上具有顯著差異。Yi等[34]的研究顯示自閉癥患者右側丘腦的度中心性顯著高于健康對照組。Zhao等[35]的研究表明自閉癥患者與健康對照組在左側梭狀回灰質體積上存在顯著差異。Weerasekera等[36]的研究發現自閉癥患者右側杏仁核的皮層下體積顯著高于健康對照組。這表明本研究所提的方法可以有效識別自閉癥的生物標志物。

2.3 分類結果

將組間差異顯著的腦區特征作為分類器的輸入構建分類模型,并從準確率、靈敏度、特異度三個方面對分類器的性能進行評價。

如表4所示,將不同方法的分類結果進行比較。首先,描述了以前傳統網絡的分類結果。其次,列舉了現有研究中將均值或標準差作為多層網絡的統計指標計算功能連接從而進行分類的結果。最后,為了消除不同研究所采用的數據和方法的差異,本研究分析了在同一數據集上分別以均值、極差、相對極差、標準差、離散系數為統計指標計算多層網絡拓撲屬性從而構建的分類器及融合上述所有特征的分類器性能。

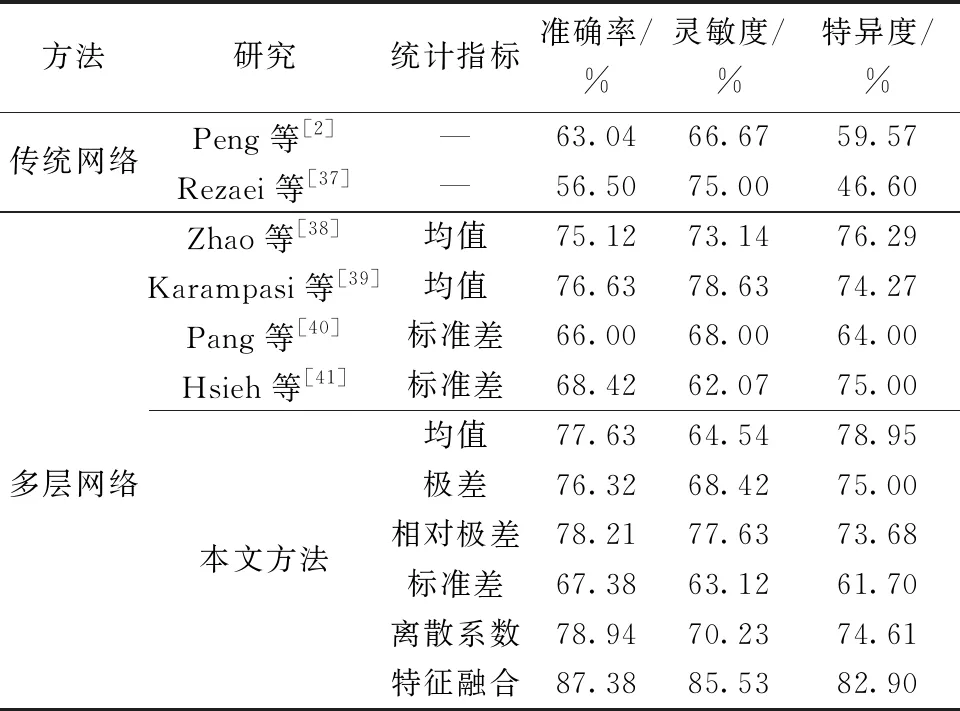
表4 不同方法的分類結果

研究結果顯示相比于傳統網絡,多層網絡具有更高的分類準確率,這與多層腦網絡包含了大腦的時變信息有關[7]。此外,無論是已有文獻,還是本研究所進行的實驗,基于相對極差視角的分類準確率均高于基于均值和標準差的分類準確率,這表明相對極差既考慮了各個單層網絡屬性的整體分布情況,又充分利用了拓撲屬性的極值信息。同時,基于離散系數視角的分類準確率高于傳統的基于均值和標準差的分類準確率,這表明離散系數在考量所有單層網絡拓撲屬性的標準差的基礎上避免了均值的影響。值得注意的是,基于極差視角的分類準確率高于基于標準差視角的分類準確率,略低于Karampasi等[39]的研究和本研究中基于均值視角的分類準確率。這可能由于基于極差的視角只應用了多個單層網絡中拓撲屬性的最大值和最小值,包含較少的信息。但是基于相對極差視角的方法應用了極差信息,而且分類效果較為理想。因此,這表明拓撲屬性中的極值信息在一定程度上有利于自閉癥的分類。此外,結果顯示基于多特征融合的分類效果最好,分類準確率為87.38%,靈敏度為85.53%,特異度為82.90%。這表明融合特征方法可以彌補從單一角度考慮多層網絡拓撲結構時缺失的信息,從而包含更多的自閉癥生物學標志物,因此可以有效提高疾病的分類表現。

由此可見,使用本研究所提出的方法可以更好地實現對自閉癥患者的分類,這為自閉癥的臨床診斷提供了一種新的思路。

2.4 特征權重

此外,使用ReliefF算法[42]分析基于均值、極差、相對極差、標準差、離散系數計算多層網絡屬性及融合所有特征對分類結果的貢獻程度。該算法依據每種類別和功能的相關性分配不同權重,分類能力越強的特征對應越大的權重。利用直方圖表示不同分類方法的權重值,并使用色塊圖表示各自方法分類權重之間的統計顯著性。如圖5所示,不同方法的分類權重存在差異。同時,與分類結果一致,基于融合特征方法的分類權重顯著高于(P<0.05)任意基于單一視角的分類權重。這表明融合特征彌補了單一統計指標缺失的信息,從多個角度綜合捕捉多層腦網絡的拓撲特征,進而更好地識別自閉癥。

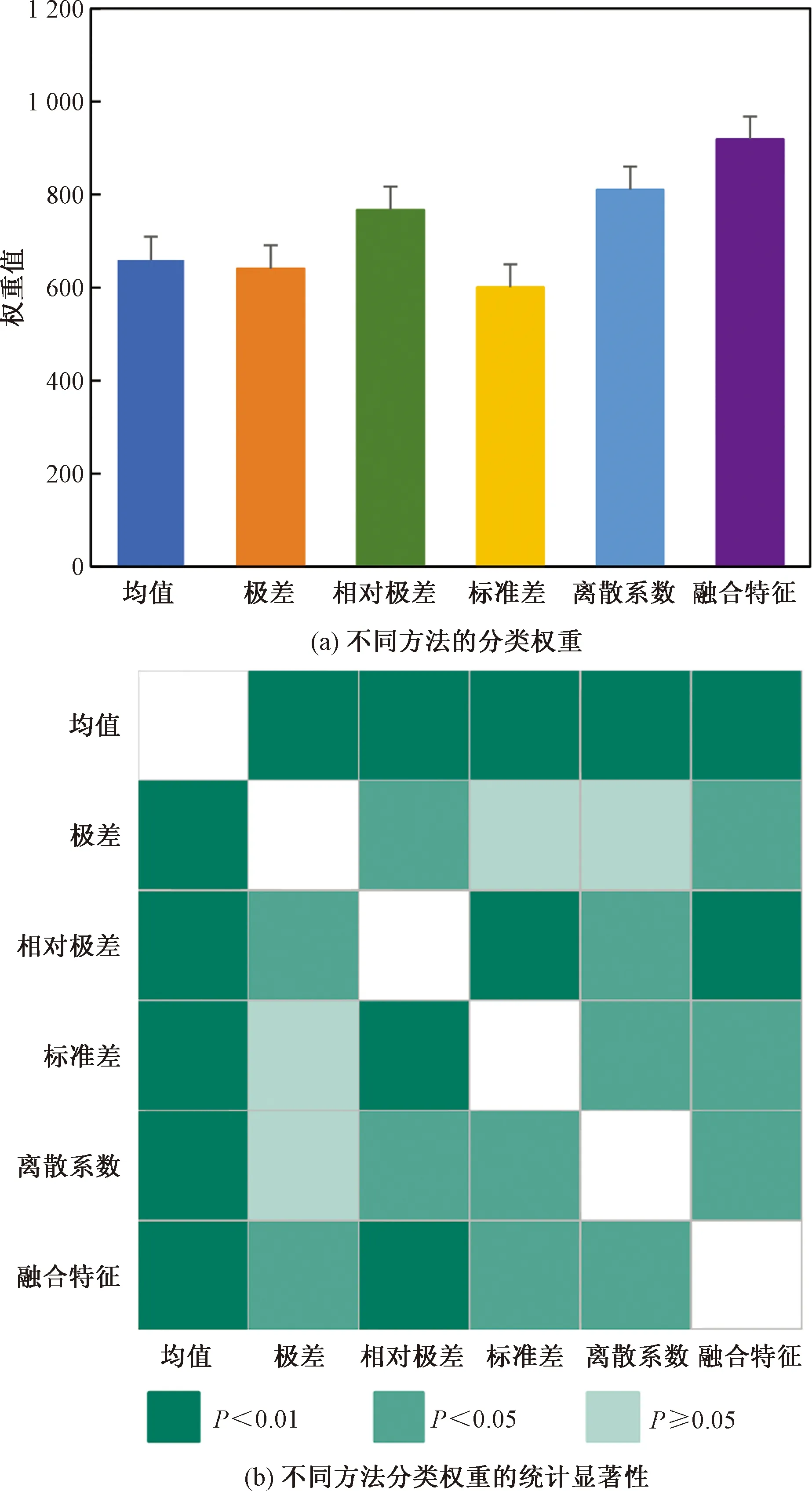
圖5 不同方法的特征權重Fig.5 Feature weights of different methods

2.5 可重復性驗證

為了驗證基于統計指標的多視角多層腦網絡拓撲屬性計算方法的可重復性,從ADNI數據集中選擇29例阿爾茨海默癥患者和30例健康被試,分別基于均值、極差、相對極差、標準差、離散系數視角計算多層網絡拓撲屬性,通過組間差異顯著的腦區特征實現分類,并對比不同多層網絡拓撲屬性計算方法及融合所有特征的方法的分類性能,具體效果如表5所示。

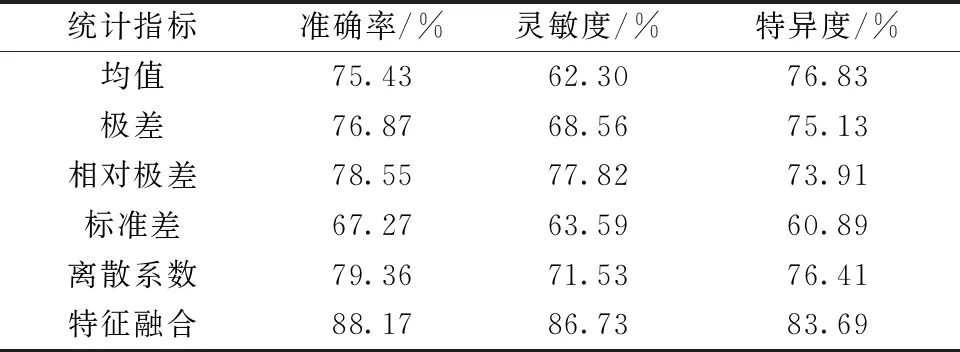
表5 ADNI數據集下不同方法的分類結果

結果顯示基于極差、相對極差、離散系數視角的分類準確率高于基于均值和標準差視角的分類準確率,同時,多視角融合特征具有最好的分類效果。這表明,本研究所提出的方法在不同的數據集下具有可擴展性,可以更有效的診斷疾病。

3 方法論

鑒于目前針對多層網絡拓撲指標的計算存在泛化性差、考量角度單一的缺點,本研究在現有的基于均值、標準差計算多層網絡拓撲屬性的基礎上提出了基于極差、相對極差、離散系數計算多層網絡拓撲屬性的方法,同時融合所有特征進行分析,從而表征大腦的時變特性,尋找組間差異特征實現對疾病的分類。雖然最終結果被證明與數據集無關,但仍會受到一些重要參數的影響,因此,本研究分析了在自閉癥數據集的實驗中涉及的參數(如滑動窗口長度、滑動窗口步長、支持向量機分類模型參數c和g)的選擇對分類準確率的影響。

3.1 滑動窗口長度

滑動窗口長度的大小會影響整體時間窗的數量和單層網絡的構建,從而最終影響多層腦網絡的構建。因此,在針對自閉癥數據集的實驗中,固定其他參數,研究滑動窗口長度分別為70、80、90、100、110、120 s時疾病的分類結果。如圖6所示,當滑動窗口長度為100 s時基于均值、極差、相對極差、標準差、離散系數及特征融合視角的方法均獲得最高的分類準確率。這表明過小的滑動窗口長度可能導致相似的時間序列被劃分到不同的窗口,從而包含很多冗余特征,造成分類結果較差。而滑動窗口長度過大使得時間窗數量較少,進而導致時變特性不明顯,因此最終的分類準確率較低。

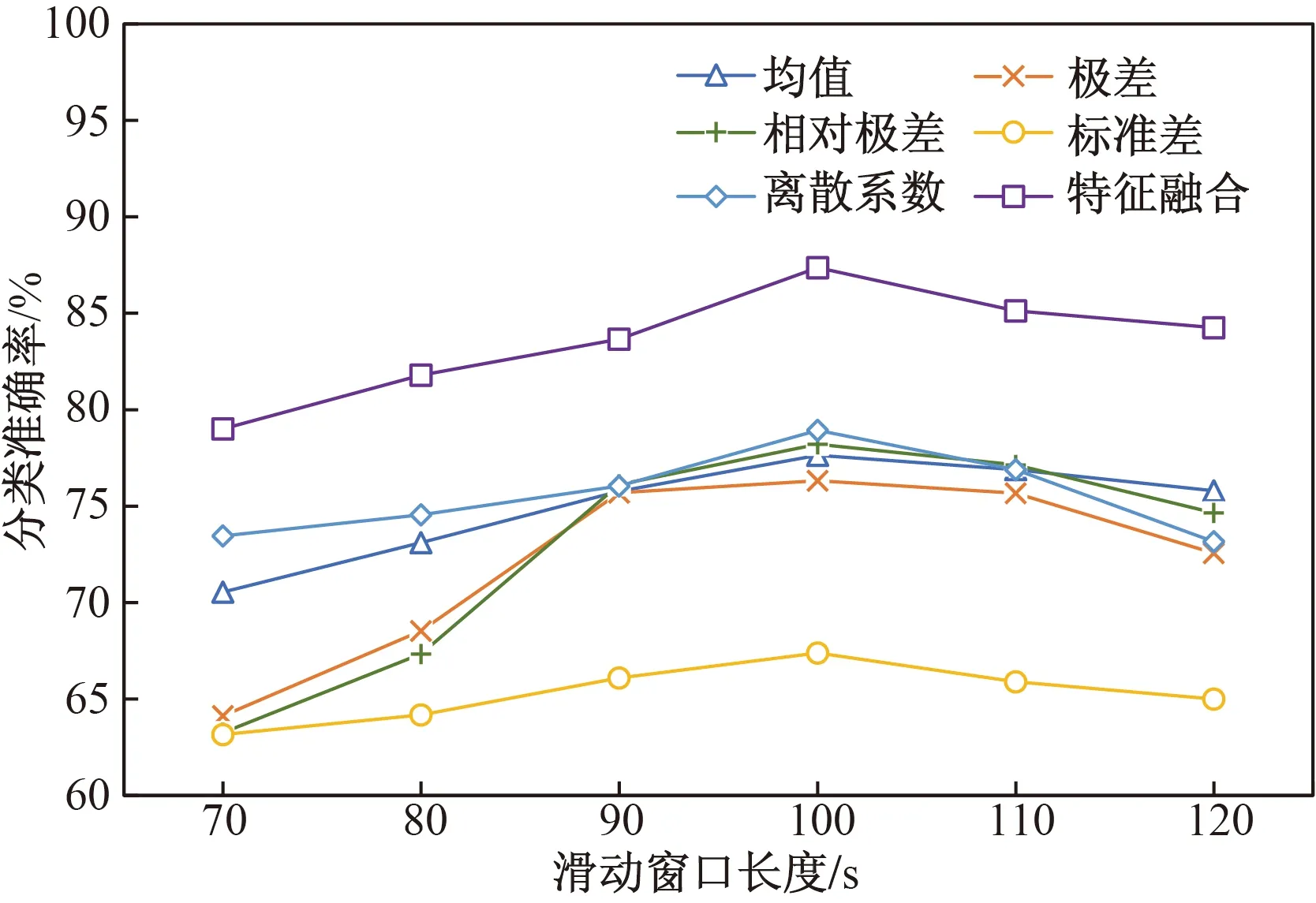
圖6 不同滑動窗口長度的分類結果Fig.6 Classification results of different sliding window lengths

3.2 滑動窗口步長

除滑動窗口長度外,滑動窗口步長也會影響多層腦功能網絡的構建。因此,如圖7所示,在固定其他參數的基礎上,研究滑動窗口步長分別為1、2、3、4、5、6 TR時自閉癥的分類結果。

圖7 不同滑動窗口步長的分類結果Fig.7 Classification results of different sliding window steps

結果顯示,當滑動窗口步長為1 TR時基于均值、極差、相對極差、標準差、離散系數及特征融合視角的方法均獲得最高的分類準確率。同時分類準確率隨著滑動窗口步長的增大而降低。這表明滑動窗口步長越大,劃分的時間窗數量越少,導致可能沒有充分體現腦網絡的時變特性,進而分類效果較差。

3.3 SVM分類模型參數的影響

SVM分類模型適用于具有高維特征和小樣本特性的數據集,被廣泛應用于腦疾病研究中。而RBF核函數不受樣本數量的影響且可以解決線性不可分問題。因此,使用RBF核函數構建分類模型。

在SVM模型中懲罰因子c和核參數g的不同取值會導致不同的分類結果。c表示對誤差的容忍度,其值過大或過小均會導致泛化能力變差;g隱含的決定原始特征數據映射到高維特征空間的分布情況,從而影響訓練和預測的速度。因此,c和g的合理組合對分類器模型的構建至關重要。

本研究在針對自閉癥數據集的實驗中,設置參數c和g的范圍為[2-8, 28],步長為1,采用網格搜索方法選取最優的c、g組合構建分類模型。具體來說,將訓練集當作原始數據集,針對每一組給定的c和g的值,使用K折交叉驗證計算分類準確率,選取最高分類準確率對應的c和g的值作為最佳參數組合。由于基于融合特征方法的分類效果最好,本研究展示了此方法下c和g的參數尋優結果。如圖8所示,當c的值為1,g的值為0.25時得到最好的訓練集驗證分類效果,其準確率為92.135%。

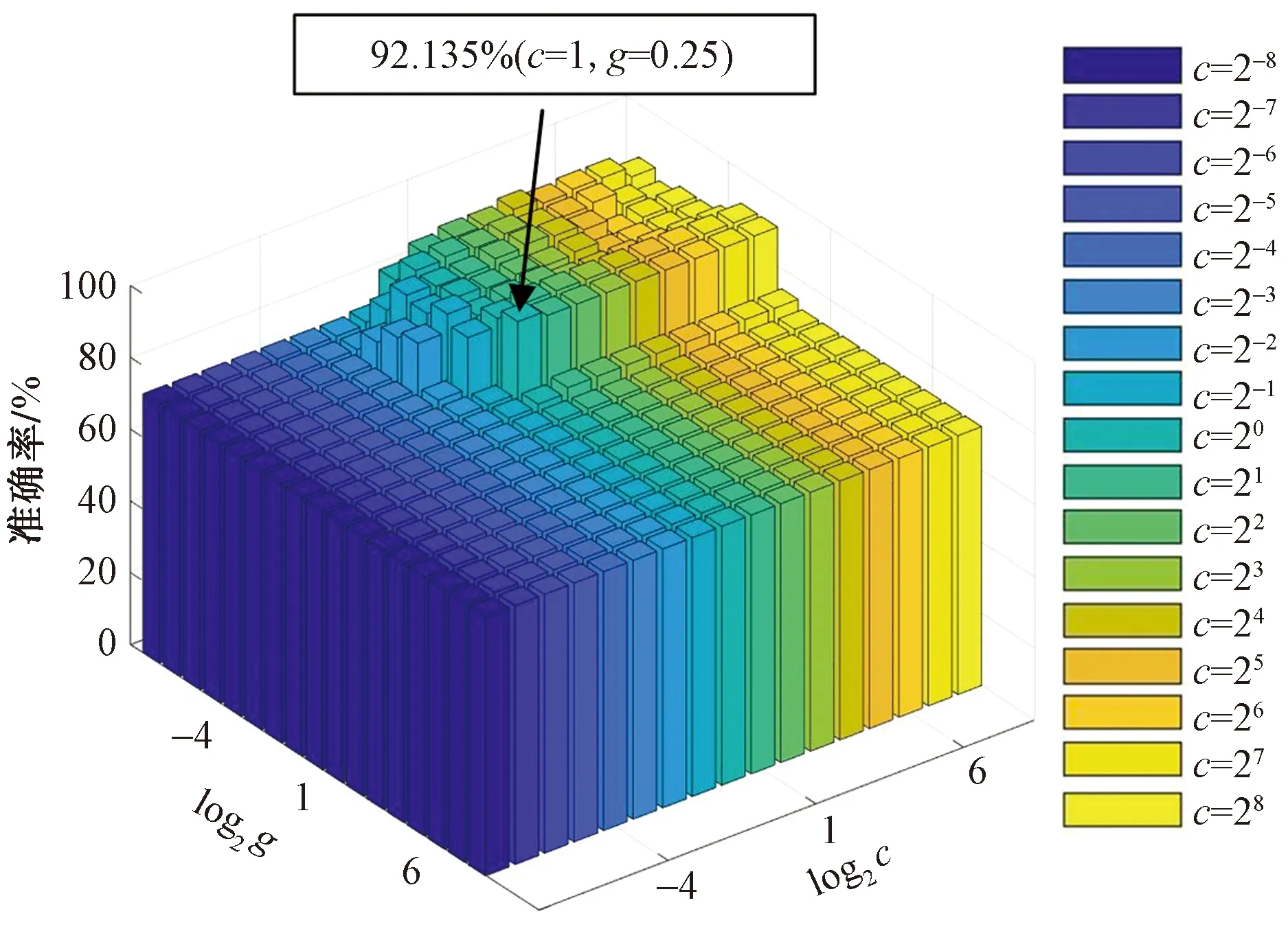
圖8 c和g的參數尋優結果Fig.8 Parameter optimization results of c and g

4 結論

本研究考慮了大腦跨腦區交互作用的時間變化,利用滑動窗口技術構建多層腦功能網絡來表征時變特性。鑒于已有的研究中針對多層網絡拓撲指標的計算方法泛化能力差、考量角度不全面的現狀,在基于均值和標準差計算多層網絡拓撲屬性的基礎上,提出了基于極差、相對極差、離散系數表征多層網絡拓撲特征,研究異常拓撲屬性并實現分類。

結果顯示,無論是ABIDE數據集還是ADNI數據集,基于相對極差、離散系數視角的分類準確率均顯著高于傳統基于均值和標準差的分類準確率,這表明本研究提出的方法可以更好地識別疾病且具有可擴展性。同時基于融合特征的分類性能優于任意單一視角下的分類性能。因此,從多個角度表征多層網絡的拓撲結構具有較好的疾病診斷效果。

但本研究仍存在局限性。首先,鑒于數據量較少實驗采用傳統統計分析方法選擇特征并使用機器學習實現分類,將來納入更多樣本后可以使用深度學習方法進行分類。其次,本研究使用度、離心率、介數中心度三個局部屬性進行分析,忽略了整體角度對多層網絡拓撲結構的影響,將來可以結合全局指標進行實驗。最后,靜態功能連接網絡和動態多層功能連接網絡為大腦交互提供互補信息,將來可以把兩者結合起來,研究其對疾病診斷的貢獻。