回音壁式耦合光力學系統中的混沌現象*

華志豪 郭琴 樊碧璇 謝旻

(江西師范大學物理與通信電子學院,南昌 330022)

在光力學系統中,輻射壓力引起的非線性可導致系統產生混沌等多種豐富的動力學行為.從有序轉變到混沌有各種各樣的途徑,本文研究了回音壁式耦合光力系統中兩種不同途徑通往混沌的現象——倍周期分岔道路和準周期道路.兩個全同的光力學子系統通過光學倏逝波進行耦合,調控子系統間的耦合強度,可以有效地改變系統的動力學行為.采用分岔圖、李雅普諾夫指數以及相空間軌跡的變化分析系統從有序到混沌的轉變.研究表明,較強的耦合強度會迫使兩個子系統的振蕩產生完全同步,子系統間相互耦合的作用可等效于子系統光學模頻率與外加控制場頻率失諧量的增加,耦合光力學系統的動力學行為等效于單個光力學系統的動力學,可實現倍周期分岔道路通往混沌的轉變.而對于相對較弱的耦合,耦合系統的動力學將在高維相空間展開,極限環發生Hopf 分岔,形成環面吸引子.選取合適的失諧量,耦合系統可實現從準周期道路進入混沌的現象.

1 引言

光力學系統[1]是研究光場和機械振子相互作用的典型模型.近年來,光力學系統的相關研究備受關注,已經成為量子光學、微納光子學等多個領域的研究對象,并且在精密測量和量子信息處理等方面展現出重要的應用價值,呈現了豐富的物理現象,如機械振子的主動冷卻[2,3]、量子糾纏[4,5]和類電磁誘導透明[6,7]等.

光力學系統中的輻射壓力可以誘導多種非線性效應.在20 世紀八十年代,光力學系統中的雙穩態就已被發現[8].近二十年來,隨著腔的品質和性能不斷提高,光力學系統中的非線性動力學得到了廣泛研究,如動態多穩性[9,10]、隨機共振[11,12]、耦合光力學系統中的同步效應[13,14]、魔鬼階梯[15]、阿諾德舌頭[16]等.

混沌是非線性動力學的一個重要分支,其實現機理是眾多研究者關注的焦點.目前已在各領域實現了多種通往混沌的途徑,如倍周期分岔道路[17,18]、準周期道路[19,20]及陣發性混沌道路[21-23]等.光力學系統因具有非線性也成為研究混沌的典型系統之一[24-29].在光力學系統中,通往混沌的道路大部分遵循倍周期分岔道路,由準周期道路通往混沌的現象鮮有研究.Roque 等[30]曾研究發現,在弱耗散的經典光力學系統中可產生準周期吸引子,實現從極限環到產生準周期運動,進而實現向混沌的轉變.這為光力學系統中產生混沌現象提供了一種新的途徑.另一方面,在連續系統中,非線性和三維及以上相空間是產生混沌的必要條件.高維相空間意味著更豐富的動力學行為[31].因此,耦合系統成為研究環面吸引子和高維混沌等動力學行為的自然候選者.在耦合系統中,環面吸引子為最常見的吸引子,但環面吸引子可能會隨著參數的變化直接失穩,從而導致混沌,即產生由準周期道路通往混沌[31-35].關于耦合系統中產生準周期道路向混沌的轉變,較早的研究可以追溯到Buskirk 和Jeffries[31]在電子電路中的實驗,他們發現改變驅動電壓時,電路中單一非線性諧振器表現為倍周期道路向混沌轉變,而兩個耦合的諧振器則表現為準周期道路向混沌轉變.隨后,有研究發現,在耦合Lorentz 系統[32,33]和耦合Duffing 振子系統[34]中不僅存在準周期運動,還存在穩定的三頻準周期運動以及高維混沌等現象.

基于上述研究背景,本文利用光學倏逝波將兩個回音壁式光力學子系統進行耦合,考慮兩個光力學子系統的系統參數完全相同,研究耦合光力系統中的混沌動力學行為.研究發現,兩個子系統間的耦合強度對于系統混沌運動的產生及其動力學過程有著重要的作用.當兩個光力學子系統間的耦合較強時,強耦合將會導致兩個子系統的動力學完全同步,兩個子系統間耦合的作用等效于改變子系統中控制場與腔場的失諧量,耦合系統可實現傳統的倍周期分岔通往混沌的現象.然而,對于兩個子系統間弱耦合的情形,耦合系統的動力學將進入高維相空間,極限環發生Hopf 分岔,形成二維環面吸引子.在合適的失諧量下,調控耦合強度,可實現二維環面吸引子向奇異吸引子的轉變,即從準周期運動通往混沌的轉變.文中采用系統的分岔圖和對應的李雅普諾夫指數譜進行詳細分析,并展示了鎖頻這一經典動力學現象.

本文的總體安排如下: 第2 節介紹本文的研究模型——回音壁式耦合光力學系統,理論推導系統的運動方程,分析無耦合情形下子系統的穩態區域;第3 節討論耦合光力學系統的非線性動力學行為,使用力學模振幅分岔圖和最大李雅普諾夫指數聯合進行分析,詳細展示了耦合系統中倍周期分岔和準周期運動向混沌的轉變行為;最后,第4 節進行了總結.

2 理論模型

本文研究的是回音壁式耦合光力學系統如圖1 所示.兩個光力學子系統a1和a2(頻率分別為ω1和ω2)通過光學倏逝波耦合,并且兩個子系統中分別包含頻率為ωm1和ωm2的力學模.采用纖維型波導分別與兩子系統的邊側耦合,用于控制場E1和E2(頻率均為ωL)的輸入與輸出.

在旋轉波近似下,該耦合系統的哈密頓量可表示為 (?=1) :

考慮壞腔極限,即光學模與力學模之間的耦合系數遠小于光場的衰變率,機械模式的零點漲落遠小于對應光學模式的線寬,因此系統的量子漲落可以忽略不計.系統隨時間演化的動力學方程可以表示為

通過線性化處理,可以得到系統的雅可比矩陣為如下形式:

其中αir和αii(i=1,2) 是腔中光學模復振幅的實部和虛部.雅可比矩陣的特征值可用于判斷系統在平衡點的穩定性以及李雅普諾夫指數的計算.

圖2 給出了兩個子系統之間無耦合的情形下(G=0 ),系統處于穩態時,力學模的位置x1隨失諧Δ1的變化曲線圖.可以看出,隨著失諧Δ1的增加,系統可由單穩態(藍色區域)演化為自持振蕩狀態(綠色區域),然后再過渡到雙穩區域.圖中小框內曲線描述了系統從單穩態區域過渡到自持振蕩區域的臨界區域內雅可比矩陣特征值的復平面圖.在該區域內,隨著失諧的微小增加,雅可比矩陣將出現一對共軛特征值——ξ和ξ?,兩特征值的虛部跨越實軸,系統發生超臨界Hopf 分岔,形成不穩定焦點,并同時產生一個穩定的極限環,系統開始自發振蕩.

圖2 兩個子系統無耦合情形下,力學模的穩態位置 x1 隨失諧 Δ1 的變化曲線圖.藍色表示穩定解,綠色表示參量不穩解,紅色表示不穩定解.小框內為雅可比矩陣的一對共軛特征值虛根變化的復平面圖.系統參數分別為κ1=1.0ωm1,γ1=0.26ωm1,g1=-0.0006ωm1,E1=2980ωm1Fig.2.System stability diagram of x1 with the varying of detuning Δ1 under uncoupling between the two subsystems.Blue stands for the stable branches,green stands for parametric instability,and red stands for unstable branch.The virtual rosots of a pair of conengenvalues for the Jacobi matrix are presented in the small box.The parameters areκ1=1.0ωm1,γ1=0.26ωm1,g1=-0.0006ωm1,E1=2980ωm1.

3 系統的混沌現象

3.1 倍周期分岔道路

本文考慮由兩個全同光力學子系統構成的回音壁式耦合系統,即兩個子系統具有完全相同的系統參數.當兩個子系統間耦合強度較強時,可產生迫使兩個子系統的振蕩完全同步的情形[36,37].為了體現強耦合導致的同步現象,圖3 給出了失諧Δ1=Δ2=-1.0ωm1時,不同耦合強度G下兩個子系統力學模位置x1和x2的輸出曲線,其中藍實線為x1的輸出曲線,紅虛線為x2的輸出曲線,系統各算符的初始平均值隨機.不難發現,當耦合強度較弱時,兩個子系統的輸出并不同步,如 圖3(a)和圖3(b)所示.然而,在較強耦合下,兩個子系統的位置輸出曲線x1和x2在時域上完全重合,即子系統之間的振蕩實現了完全同步,如圖3(c)—(f)所示.而且在強耦合下,隨著G的增加,系統的動力學行為也有顯著改變,其輸出從有序化的周期振蕩逐步轉變為無序化振蕩.當兩個子系統耦合強度為G=1.7ωm1,位置輸出曲線為單周期振蕩,如圖3(c)所示,圖中以黑色框標記單周期.繼續增強耦合強度G,振蕩周期也不斷增大,由單周期振蕩變為倍周期、四周期乃至無周期振蕩.圖3(f)中的無周期運動表明系統很可能已經進入了混沌狀態.

圖3 不同耦合強度下兩個子系統力學模位置的輸出曲線,藍實線對應 x1 ,紅虛線對應 x2 (a) G=1.0ωm1 ;(b) G=1.5ωm1 ;(c) G=1.7ωm1 ;(d) G=2.3ωm1 ;(e) G=2.8ωm1 ;(f) G=3.0ωm1 .兩個子系統參數完全相同,初始條件隨機,Δ1=Δ2=-1.0ωm1,其余參數和圖2 相同Fig.3.Output curves of the two mechanical modes under different coupling strengthes.The blue solid line and the red dashed line correspond to x1 and x2 ,respectively: (a) G=1.0ωm1 ;(b) G=1.5ωm1 ;(c) G=1.7ωm1 ;(d) G=2.3ωm1 ;(e) G=2.8ωm1 ;(f) G=3.0ωm1 .The parameters for the two subsystems are exactly the same,and the initial conditions are arbitrary.All parameters are the same as those in Fig.2 except for Δ1=Δ2=-1.0ωm1 .

當系統在強耦合下迫使兩個子系統達到完全同步時,兩個子系統力學量的穩態值在任意時刻均相等,光學模的復振幅也不例外,即α1=α2.系統的動力學方程中(2)式可改寫為

為了定量分析耦合系統的動力學行為,進一步給出了強耦合下x1的振幅隨兩個子系統間耦合強度變化的分岔圖以及最大李雅普諾夫指數圖,如圖4 所示.李雅普諾夫指數是表示相空間相鄰軌跡的平均指數發散率的數值指標.該指數越大,表示系統的局域穩定性越差,當其大于零時,則代表系統處于混沌狀態.觀察分岔圖可以得知,隨著耦合強度的增強,x1的振蕩從單周期開始,隨后周期逐步加倍,直至無周期振蕩.對于無周期區域,最大李雅普諾夫指數λ1皆為正值,表明在這些區域,系統已經進入混沌狀態.隨著耦合強度的增加,系統的動力學行為的周期數倍增,直至進入混沌狀態,這種現象被稱為倍周期分岔,也是單個光力學系統中通往混沌最常見的途徑[25].耦合系統的倍周期分岔路徑的產生正是由于單個子系統在失諧的區域存在一個對應的倍周期分岔現象.強耦合的作用迫使兩個子系統的振蕩完全同步,因此耦合光力學系統的動力學行為等效于單個光力學系統,實現了倍周期分岔道路向混沌的轉變.

圖4 (a)系統倍周期分岔圖;(b)最大李雅普諾夫指數圖.所有參數和圖3 相同Fig.4.(a) Schematic period-doubling bifurcation diagram;(b) the curve for the maximum of Lyapunov exponents.All parameters are the same as those in Fig.3.

3.2 準周期道路

接著,進一步考慮兩個全同子系統間的耦合強度相對較弱的情形.強耦合可迫使兩個子系統的動力學完全同步,耦合系統的動力學行為與單個子系統的維度相同,只在四維相空間展開,這被稱為同步流形,而完全同步下出現的混沌可被稱為同步混沌.在相對較弱的耦合下,子系統之間的振蕩具有相干性,耦合系統的動力學行為將在高維相空間展開.此時,通過調節光學耦合強度,可誘導極限環發生超臨界Hopf 分岔,產生環面吸引子,這為耦合系統產生準周期路徑提供了先決條件.為了可觀測到耦合系統的環面失穩,實現準周期路徑通往混沌的轉變,還需系統處于容易產生復雜動力學行為的參數區域范圍內.倘若在合適的失諧量下,強耦合迫使兩個子系統達到完全同步時,系統已經處于或接近處于同步混沌狀態,那么這就為相對較弱耦合時產生環面失穩并通往混沌提供了可能.為此,選取失諧為Δ1=Δ2=0.5ωm1,調節耦合強度,研究耦合系統從準周期運動向混沌的轉變.

圖5 給出了兩個子系統在失諧Δ1=Δ2=0.5ωm1時,不同耦合強度下系統的三維相空間圖I1(a1腔光子數)-x1-p1的軌跡、二維相空間圖x1-x2的 軌跡、李雅普諾夫指數譜以及x1的頻率譜.為了體現混沌對初始條件的敏感度,圖5 給出了兩組初始條件下三維相空間圖的軌跡,其中第一組初始條件是隨機生成的,第二組初始條件與第一組的區別是初始的x1被增加了 10-5,圖中利用兩種不同顏色進行表征.其余三個子圖只展示了系統為第一組初始條件下的結果.在無共存吸引子的情況下,系統在任意初始條件下的功率譜和李雅普諾夫指數譜的特征穩定.二維相空間則很好地體現了兩個子系統動力學的關系.

圖5 不同耦合強度下 系統 達到 穩定時的狀態圖 (a) G=1.47ωm1 ;(b) G=1.53ωm1 ;(c) G=1.60ωm1 ;(d) G=1.87ωm1 .其中每張子圖中包含4 個分圖,左上圖對應 I1-x1-p1 三維相空間軌跡,兩種顏色表征兩組初始條件下的軌跡;左下圖對應x1-x2二維相空間軌跡;右上圖對應動態李雅普諾夫指數譜(前4 個李雅普諾夫指數);右下圖對應 x1 的頻率譜.Δ1=Δ2=0.5ωm1,其余參數和圖3 相同Fig.5.Stability diagrams of the system under different coupling strengthes: (a) G=1.47ωm1 ;(b) G=1.53ωm1 ;(c)G=1.60ωm1 ;(d) G=1.87ωm1 .Each subgraph includes four charts,the top left one corresponding to the three-dimensional phase space of I1-x1-p1,and the two colors represented the traces for two sets of initial conditions;the bottom left one corresponding to the two-dimensional phase space of x1-x2 ;the top right one corresponding to Lyapunov exponents (the top four Lyapunov exponents);and the bottom right one corresponding to the frequency spectrum of x1 .The other parameters are the same as those in Fig.3 except for Δ1=Δ2=0.5ωm1 .

為了區分極限環和極限環面,借助李雅普諾夫指數譜來判斷吸引子的類型.系統具有八維相空間,擁有8 個李雅普諾夫指數.在數值模擬中,從大到小排列,李雅普諾夫指數的第4 個值表現為穩定負值,因此圖5 只給出了前4 個李雅普諾夫指數λi(i=1,2,3,4).當兩個子系統間的耦合強度G=1.47ωm1時,三維相空間圖顯示吸引子為標準二維環面,如圖5(a)所示.在李雅普諾夫指數譜中,λ1和λ2重合在 0 處,而λ3和λ4為負值,表明吸引子屬于 (0,0,-,-,···) 型,對應二頻準周期運動.而在x1的頻率譜中,其主頻峰ω01以左出現了一個不可公度的新頻率ω02,譜中所有頻率分量都可以表示為這兩個基本頻率的線性組合,這也是二頻準周期運動的表征.當耦合強度增強到G=1.53ωm1時,如圖5(b)所示,三維相空間圖表明吸引子出現了分形結構的趨勢,而李雅普諾夫指數λ1上升為正值,說明系統已經處于混沌狀態.不難看出,即使兩組在具有微小差別的初始條件下,三維相空間圖有著完全不同的兩組軌跡(兩種不同的顏色表征),表明混沌對初始條件非常敏感,這是混沌的特點之一.然而整體上,兩組軌跡又被限制于相同的區域,這是因為吸引是耗散系統的整體性質.相較于圖5(a),x1的頻率譜細峰逐漸消失,并且峰值也有所降低,此時系統剛剛過渡到混沌,混沌的特征還不夠明顯.繼續增強耦合強度,G=1.60ωm1,如圖5(c)所示,相較于圖5(b),λ1明顯上升,x1的頻率譜展現出混沌的標準特征,即寬峰和類似噪聲的整體譜線.三維相空間圖出現了奇異吸引子的特征,即明顯的分形結構.然而,當耦合強度達到G= 1.87ωm1時,x1-x2二維相空間圖為一條關于x1-x2對稱的直線,如圖5(d)所示.這是兩個子系統動力學行為完全同步在相空間的體現,過強的耦合強度導致子系統的振蕩完全同步.結合李雅普諾夫指數(λ1的正值)以及與圖5(c)類似的功率譜,說明此時耦合系統處于同步混沌的狀態.

下面仍以x1的振幅隨耦合強度變化的分岔圖以及李雅普諾夫指數譜來詳細分析系統從準周期道路向混沌的轉變過程,圖6 給出了系統的分岔圖和李雅普諾夫指數圖.x1的振幅分岔圖中顯示,隨著耦合強度的增大,系統的動力學過程歷經了極限環、準周期運動、有限周期運動以及由準周期運動向混沌狀態的轉變.當耦合強度G較小時,系統的振蕩是單周期的極限環,其相應的李雅普諾夫指數譜中最大值λ1為零,λ2和λ3為相等的負值.隨后,λ2和λ3開始分離,λ2上升至零并保持為零,而λ3則下降,依然為負值.這表明極限環發生了超臨界Hopf 分岔,轉變為穩定的二維環面[38],即準周期運動.x1的振幅變得稠密,而且x1的頻率譜上將會出現兩個不可公度的基本頻率.隨著耦合強度的增強,兩個基本頻率會發生微小移動.如果滿足兩個基本頻率之比為有理數,系統將出現鎖頻現象,并且系統的動力學行為由準周期運動轉變為有限周期運動.如此交替變化,兩種動力學現象交替的間隔越來越小,直至系統完全處于準周期運動狀態.然而繼續增強耦合強度,系統將出現環面失穩,開始由準周期運動向混沌狀態的轉變,其標志是分岔圖中下邊界不再清晰.而系統處于混沌狀態的另一標志是李雅普諾夫指數λ1急劇上升,變為大于零的正值,同時λ2上升至零的位置,在這個范圍內吸引子擁有環面的形狀,如圖5(c)所示.當耦合強度過強時,系統的動力學行為再次出現了突變,李雅普諾夫指數譜也有一個明顯的變化,λ3先上升為零,隨后立刻下降為負值,與λ4基本保持相等.強耦合導致了兩個子系統振蕩完全同步,引起了同步混沌的現象,這與圖5(d)所示結果完全符合.同步混沌的發生為耦合系統產生環面失穩給予了很好的解釋.混沌往往發生于系統處于容易產生復雜動力學行為的參數區域內.雖然強耦合導致的同步混沌不是高維相空間的產物,但其發生區域依然是系統動力學劇烈變化的區域,并且具有魯棒性.因此,調節光學耦合強度,使環面吸引子不斷靠近同步混沌時,將會激起耦合系統產生復雜的動力學行為,從而產生環面失穩變為奇異吸引子,實現從準周期路徑通往混沌的轉變.

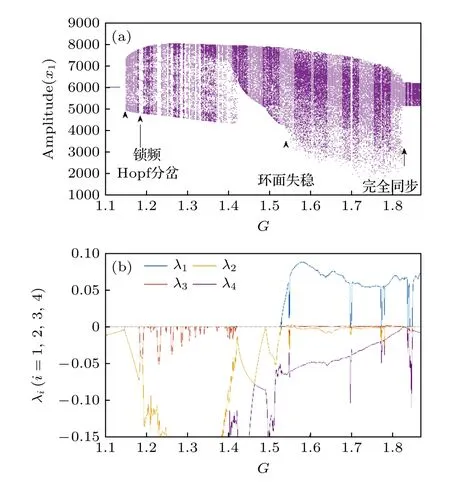
圖6 (a)準周期路徑分岔圖;(b)李雅普諾夫指數圖(前4 個李雅普諾夫指數).所有參數與圖5 相同Fig.6.(a) Schematic quasiperiodic bifurcation diagram;(b) curves of Lyapunov exponents (the top four Lyapunov exponents).All parameters are the same as those in Fig.5.

4 結論

綜上所述,本文利用光學倏逝波耦合兩個回音壁式全同光力學子系統,從理論上研究了該耦合系統中兩個子系統間的相互耦合對系統產生混沌現象的影響.調控兩個光力學系統之間的耦合強度,耦合系統可實現倍周期分岔道路和準周期道路進入混沌的轉變.倍周期分岔的產生原因是由于強耦合迫使兩個子系統的振蕩完全同步,使得在強耦合下調制耦合系統的耦合強度等效于改變了子系統光學模頻率與外加控制光場頻率的有效失諧量,耦合系統的動力學可退化為單個光力學系統的動力學過程,實現倍周期分岔通往混沌的道路.對于較弱的耦合,系統的動力學將進入高維相空間,極限環發生Hopf 分岔,形成環面吸引子.選取合適的失諧量,系統可實現環面失穩,從而產生從準周期道路進入混沌的現象.

感謝江西師范大學物理與通信電子學院段正路教授的討論.