考慮環空液體熱力學特征的持續環空帶壓預測模型研究

丁亮亮,代先濤,李帥,張強

(1.西南石油大學機電工程學院,成都 610500;2.中石化西北油田采油一廠,巴音郭楞蒙古自治州 841602)

近年來,持續環空帶壓已成為氣井普遍存在問題,特別是塔里木油田及西南油氣田氣井持續環空帶壓問題尤為嚴重[1-3]。持續環空帶壓是指井口環空壓力泄放后短時間內又恢復到泄壓前水平的現象[4]。油管、套管及水泥環等井生產安全屏障組件密封失效是其產生的主要原因[5-6]。持續環空帶壓不僅增加了氣井管理難度、降低氣井采收率,嚴重時甚至會導致井口裝置破損失效,造成巨大經濟損失及安全事故[7-9]。

因此,急需開展氣井持續環空帶壓特征及機理研究。針對氣井環空帶壓問題的研究最早可追溯到20世紀80年代,外國學者最先研究了環空帶壓產生機理并提出了持續環空帶壓概念。學者們深知持續環空帶壓的產生影響因素多、危害大,因此從未停止過這方面的研究。張波等[10]為探究通過水泥返高調控持續環空壓力的可行性,建立了基于物質守恒和體積守恒的含液環空持續環空壓力計算模型。羅偉等[11]展開了油管多漏點泄漏規律及控制研究,將多漏點泄漏分為多種情況并利用現場實例驗證了所提出漏點的合理性。李磊等[12]基于氣體滲流方程,利用水泥環綜合滲透率表征水泥環失效程度,建立了考慮氣體溶解的持續環空壓力預測模型。Zhang等[13]建立了由多油管泄漏點引起的持續環空壓力模型并分析了泄漏率、環空持續壓力與流體分布之間的耦合關系。練章華等[14]建立了油套環空帶壓預測模型,并利用模型對油管漏點當量直徑進行了擬合。Kazemi等[15]提出了一種改進的環空帶壓測試方法,并指出漏壓為0并不一定意味著泄漏很小,還取決于水泥頂部環空液柱的高度和性質。閻衛軍等[16]為準確預測套管環空上方的持續環空壓力,將環空竄流等效滲透率計算方法補充到持續環空壓力預測模型。

以上學者針對氣井持續環空帶壓的研究具有重要的參考價值及意義。但學者們在建模過程中均未考慮環空溫壓變化所引起的環空液體膨脹或收縮效應,并且學者們均將環空液體壓縮系數視為定值,并未考慮溫壓耦合作用[17]下對環空液體熱膨脹系數、壓縮系數影響。然而這兩個系數是預測環空壓力基礎性、關鍵性參數[18]。為此,考慮溫壓耦合作用對環空液體熱力學性質影響,建立一種新的環空帶壓數學預測模型,以井筒溫壓場預測數據及A氣井現場實測數據為基礎,驗證模型的準確性,利用模型對A氣井進行了環空壓力診斷及不同參數對環空壓力、氣柱高度的影響分析,為現場環空帶壓預測及管理提供理論支撐。

1 力學模型

油管氣體在油管漏點內外壁壓力差作用下泄漏至環空并在井口聚集,最終形成環空帶壓,如圖1所示。在氣體泄漏至環空過程中由于井筒傳熱會導致環空溫度變化,影響環空液體熱膨脹系數、壓縮系數,最終影響環空壓力預測準確性。

圖1 氣井結構示意圖Fig.1 Gas well structure diagram

為此首先建立井筒溫壓場預測模型,利用井筒溫壓場預測模型預測油管內溫度、壓力及油套環空溫度。隨后充分考慮溫壓耦合作用對環空液體熱力學參數影響,建立持續環空帶壓預測模型。最后,以井筒溫壓場預測數據為基礎,結合現場數據驗證所建模型準確性,利用模型對氣井環空壓力恢復過程進行診斷并分析不同參數對環空壓力、氣柱高度影響。

1.1 井筒溫壓場預測模型

氣井測試過程中,井筒溫度場變化遵循質量守恒、動量守恒、能量守恒方程及狀態方程,井筒溫度、壓力可通過式(1)求得。

(1)

式(1)中:下標g、t、ti分別表示油管內流體、油管柱和油管內壁面;ρ為氣體密度,kg/m3;v為氣體流速,m/s;z為井深,m;t為時間,s;c為比熱,J/(kg·K);hti為油管內壁對流換熱系數,W/(m2·K);kg為氣體熱傳導系數,W/(m·K);T為溫度,K;d為管柱直徑,m;f為壁面摩阻系數,無量綱;p為壓力,MPa;γg為氣體相對密度,無量綱;Zg為氣體偏差因子,無量綱;rti為油管內徑,m;0.016為天然氣的摩爾質量,kg/mol;R為氣體常數,R=8.314 Pa·m3/(mol·K)。

式(1)中摩阻系數f與流體流態相關,不同流態下氣體摩阻系數可通過式(2)式求得[19]。

(2)

式(2)中:Re為雷諾數,無量綱。

雷諾數為判斷流體流動狀態的判據,可通過式(3)計算。

(3)

式(3)中:υ為運動黏度,m2/s。

不同井筒流體流動情況下壁面對流換熱系數h與流體流速、流體密度、比熱、黏度、導數系數等參數有關,對流系數可通過式(4)計算。

(4)

1.2 環空壓力預測模型

1.2.1 氣體泄漏流量計算

(5)

(6)

式中:Qc為標況下氣體流量,m3/d;d1為漏點當量直徑,mm;T1為油管漏點外壁溫度,K;k為絕熱指數,通常取1.28;pti、pto分別為油管漏點內、外壁壓力,MPa。

1.2.2 油管漏點外壁壓力計算

流體密度是溫度及壓力的函數,而環空軸向上不同位置處環空壓力、溫度并不相同,因此流體密度也不相同。為了更加精確求解油管外壁壓力,將整個環空沿軸向劃分為若干個網格,則油管外壁壓力計算公式為

(7)

Ellis等[20]、Oudemanp[21]研究發現,環空液體物理性質與水的物理性質相似,因此借助文獻[22]中溫度為27、107、127 ℃,壓力為1、10、100 MPa下水的密度數據,利用二元拉格朗日插值法擬合密度關于溫度及壓力多項式[22],如式(8)所示。

ρL=P(a1T3+a2T2+a3T+a4)+

P2(a5T3+a6T2+a7T+a8)+

a9T+a10T2+a11T3+1 002.01

(8)

式(8)中:ρL為水的密度,kg/m3;P為壓力,MPa;T為溫度,℃;a1=-2.057 61×10-8;a2=1.958 33×10-5;a3=-2.008 28×10-3;a4=4.944 26×10-1;a5=-2.338 20×10-11;a6=-3.598 48×10-8;a7=3.883 58×10-6;a8=-5.495 44×10-4;a9=-3.598 48×10-8;a10=3.883 58×10-6;a11=-5.495 44×10-4。

為驗證擬合公式準確性,利用式(8)計算溫度為177 ℃,壓力為1、10、100 MPa下水的密度并與文獻[22]中密度進行對比,對比結果如表1所示。可以看出,最大誤差僅為0.16%。

表1 公式計算的密度值與文獻[22]對比Table 1 The equation calculates the density of water and compares it with the ref.[22] value

1.2.3 環空體積變化量及環空帶壓值計算

液體熱膨脹性、壓縮性是導致環空體積變化的主控因素。而液體熱膨脹系數、壓縮系數是密度分別與溫度、壓力的導函數,計算公式分別為

(9)

(10)

式中:CT為環空液體熱膨脹系數,K-1;Cm為環空液體壓縮系數,MPa;V為液體體積,m3;dV為液體體積變化量,m3;dT為液體溫度變化量,K;dρ為液體密度變化量,kg/m3;dp為壓力變化量,MPa。

將式(8)分別對溫度、壓力求導后代入式(9)、式(10)得到熱膨脹系數、壓縮系數計算公式分別為

P2(3a5T2+2a6T+a7)+a9+

2a10T+3a11T2]

(11)

2P(a5T3+a6T2+a7T+a8)]

(12)

利用式(13)計算溫度為7～175 ℃、壓力為1～100 MPa下水的密度,求導后分別代入式(11)、式(12)求得熱膨脹系數、壓縮系數如圖2所示。可以看出,水的熱膨脹系數及壓縮系數隨溫度及壓力的增加而不斷增大,且兩者溫度、壓力由7 ℃、1 MPa增大至175 ℃、100 MPa后,熱膨脹系數、壓縮系數分別增大了7.16倍、2.07倍,由此可知溫度、壓力對熱膨脹系數、壓縮系數有較大的影響。因此,在計算環空液體體積變化時采用不同溫度及壓力下的熱膨脹系數、壓縮系數。

圖2 水熱力學參數隨溫壓變化等高圖Fig.2 Contour diagram of water thermodynamic parameters varying with temperature and pressure

氣體泄漏至環空過程中,環空壓力值與時間密切相關,將環空壓力恢復周期分為若干個時間微元,時間步長為Δt,第x時間段內由于井筒溫度變化而導致環空液體體積變化量可由式(13)計算。

(13)

由于壓力升高導致環空液體壓縮總體積可由式(14)計算。

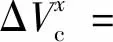
(14)

假設油管及套管為剛性材料,環空總體積保持不變,即環空內氣體與液體體積變化量相等,規定使氣體體積增大為正,環空氣體體積變化量可由式(15)計算。

(15)

根據PVT方程,環空氣柱滿足式(16)。

(16)

(17)

將式(13)、式(15)代入式(14)得到第x時刻環空壓力計算公式為

(18)

1.3 模型求解

井筒溫壓場預測及持續環空壓力預測模型求解步驟如下。

步驟3重復步驟1、步驟2直至算至封隔器位置。

步驟5再次判斷油管內外壁壓力是否滿足精度,若滿足精度結束運算,否則執行步驟1、步驟2。

2 實例分析

2.1 基礎參數

塔里木盆地克深氣田高壓氣井-A井2016年10月4日投產,完井深度7 720 m,地溫梯度2.35 ℃/100 m;隨后油套環空壓力隨生產制度反復波動,最后2019年3月油套連通。其井身結構和流體相關參數如表2所示。

表2 A氣井井深結構及流體相關參數Table 2 Well depth structure and fluid related parameters of a high temperature and high pressure gas well

2.2 環空壓力預測模型對比分析

圖3為環空壓力實測數據與模型預測數據對比。可以看出,考慮溫度壓力對環空液體熱膨脹系數、壓縮系數影響所建立模型環空壓力預測數據與實測數據相比平均精度高達96.05%,而未考慮溫度壓力對環空液體熱膨脹系數、壓縮系數的影響,模型平均精度為94.86%。即所建立的模型預測數據更具參考價值。

圖3 實測數據與模型預測數據對比Fig.3 Comparison of measured data and model prediction data

2.3 環空壓力恢復過程診斷分析

利用所建模型對A氣井進行環空壓力恢復過程模擬研究,環空壓力及漏點流量隨時間變化關系如圖4所示。可以看出,A氣井環空壓力穩定至為82.22 MPa,環空壓力從49.57 MPa恢復到穩定值需75 h。在環空壓力恢復過程中油管漏點流量與時間呈拋物線關系,最大泄漏流量為1 931.23 m3/d。

圖4 環空壓力及漏點流量隨時間變化圖Fig.4 Diagram of annulus pressure and leakage flow over time

圖5為環空壓力恢復過程中環空氣柱高度隨時間變化,可以看出,環空壓力恢復至約50 h時氣柱高度達到最大值1 215.87 m,隨后下降至1 209.60 m,即該井氣柱高度隨時間延長呈先增大后減小趨勢。

圖5 環空壓力恢復過程中環空氣柱高度隨時間變化圖Fig.5 Diagram of the height of the ring air column changing with time during air pressure recovery

2.4 環空壓力可調控因素敏感性分析

影響氣井環空壓力恢復過程及氣柱高度變化的因素主要包括漏點大小、漏點位置、環空液體密度、氣柱高度、環空壓力及環空溫度。其中漏點大小及漏點位置為不可控因素,而對于已油套聯通的井環空液體密閉對環空壓力值影響不大,因此主要研究初始環空氣柱高度、壓力及溫度對環空壓力恢復過程及氣柱高度影響規律。

圖6為初始氣柱高度對環空壓力恢復過程影響,可以看出,當氣柱高度hg=596.34 m時,環空壓力穩定值為76.04 MPa,而當hg=1 196.34 m時,環空壓力穩定增大至82.22 MPa,增加了6.18 MPa。即隨著環空氣柱高度的增加,環空壓力穩定值隨之增大。但在環空壓力未達到穩定值前,同一時刻氣柱高度越低環空壓力值越高,由此可知氣柱高度越高環空壓力恢復速度越快。因此應結合井實際情況預留一定環空氣柱高度,有利于降低環空壓力恢復速度。

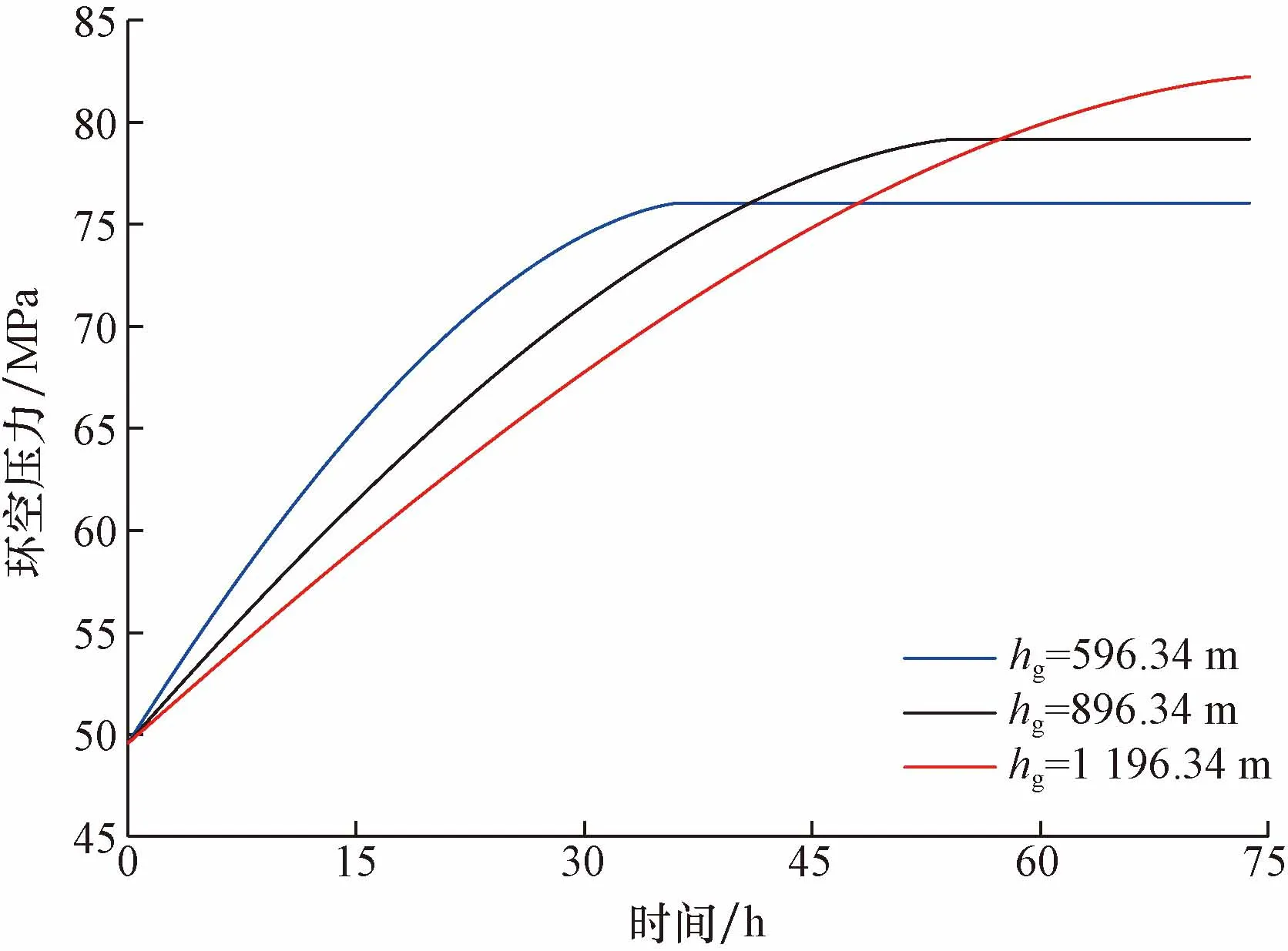
圖6 初始氣柱高度對環空壓力恢復過程影響圖Fig.6 Diagram of influence of initial column height on annular pressure recovery process

圖7為環空壓力恢復過程中氣柱高度隨時間變化。可以看出,初始氣柱高度越低,環空壓力恢復到穩定值后氣柱高度變化越大。這是因為,氣柱高度越低則環空液體體積越大,根據體積守恒原則,經過環空壓力恢復過程后氣柱高度變化越大。

圖7 環空壓力恢復過程中氣柱高度隨時間變化圖Fig.7 Diagram of column height variation with time during annulus pressure recovery

因為環空液體熱膨脹系數、壓縮系數是溫度及壓力的函數。井口環空溫度不同將導致兩個系數的不同。為此環空溫度T分別取40、60、80 ℃,進行環空壓力恢復過程模擬,模擬結果如圖8所示。可以看出,環空溫度對環空壓力穩定值基本無影響,但對環空壓力恢復速度有影響。同一時刻環空溫度越低,環空壓力值越低。因此建議在完井時使用傳熱效率低的管柱及環空液體,有利于降低環空壓力恢復速度。

圖8 初始環空溫度對環空壓力恢復過程影響Fig.8 Influence of initial annulus temperature on annulus pressure recovery process

圖9為初始環空溫度對環空壓力恢復中氣柱高度的影響。可以看出,當T=40 ℃時,經過環空壓力恢復過程后,氣柱高度由1 193.34 m變為1 203.59 m,當T=80 ℃時,氣柱高度由1 193.34 m變為1 206.62 m。由此可知氣柱高度變化量與環空溫度呈正相關。

圖9 初始環空溫度對環空壓力恢復中氣柱高度影響Fig.9 Influence of initial annulus temperature on column height in annulus pressure recovery

不同環空壓力對環空壓力恢復過程影響如圖10所示。可以看出,當Pa=29.57 MPa時,環空壓力恢復到穩定值需約90 h,即平均環空壓力恢復速度為0.585 MPa/h;當Pa=39.57 MPa時,經過74 h后環空壓力達到穩定值,即平均恢復速度為0.576 MPa/h;當Pa=49.57 MPa時,環空壓力恢復到穩定值需要約58 h,即平均恢復速度為0.563 MPa/h。由此可知,初始環空壓力越大環空恢復速度越小。因此在保證井筒安全情況下,建議預留一定環空壓力。

圖10 初始環空壓力對環空壓力恢復過程影響Fig.10 Influence of initial annulus pressure on annulus pressure recovery process

圖11為初始環空壓力對環空壓力恢復中氣柱高度影響。可以看出,Pa=29.57 MPa,環空氣柱高度最終為1 227.91 m,而當Pa=49.57 MPa時,經過環空壓力恢復過程后氣柱高度變為1 197.75 m。即環空氣柱高度隨環空壓力的增大而減小。

圖11 初始環空壓力對環空壓力恢復中氣柱高度影響Fig.11 Influence of initial annular pressure on column height in annular pressure recovery

3 結論

(1)在前人研究基礎上,充分考慮溫壓耦合作用對環空液體熱力學參數影響,建立了新的持續環空帶壓預測模型;利用該模型對A氣井進行環空壓力預測并與實測數據進行對比,所建模型預測平均精度高達96.05%,而未考慮溫壓影響的預測模型平均精度為94.86%,因此所建立模型預測數據更具有參考價值。

(2)利用所建立模型對A氣井進行環空壓力恢復過程模擬,結果表明該井環空壓力穩定值為82.22 MPa,漏點最大流量為1 931.23 m3/d;環空壓力恢復過程中環空氣柱高度隨時間增加呈先增大后減小趨勢。

(3)利用模型對初始環空氣柱高度、溫度及壓力可調控因素進行了環空壓力及氣柱高度敏感性分析,結果表明:預留一定環空氣柱高度、壓力及降低環空溫度有利于降低環空壓力恢復速度;氣柱高度變化量隨環空氣柱高度及壓力增大而減小,隨環空溫度增大而增大。