耦合多孔介質層的內產熱腔體雙擴散自然對流

胡江濤,蔣文濤,梅碩俊

(1.中南林業科技大學土木工程學院,長沙 410004;2.中山大學大氣科學學院,珠海 519082)

由溫度梯度與濃度梯度同時驅動的雙擴散自然對流廣泛存在于自然界與工業應用中,在過去幾十年內受到越來越多的關注[1-2]。與純溫度梯度引起的自然對流不同,雙擴散自然對流中存在著溫度與濃度的擴散且兩種擴散之間會有相互作用,從而對流動產生復雜的影響。其中鹽梯度太陽池的蓄熱過程是一種典型的雙擴散自然對流現象[3-4]。在鹽池的蓄熱過程中,下對流層溫度不斷升高,上、下對流層存在越來越大的溫差與濃度差,最終非對流層的靜止狀態被打破,導致下對流層發生熱逃逸,鹽池的蓄熱能力降低。為了提升鹽池蓄熱能力,多孔介質層由于其良好的保溫隔熱能力,被應用于鹽池底部。研究表明,多孔介質層隔絕了鹽池底部與地面的熱交換,避免了熱量損失,蓄熱能力提高[5-6]。因此,理解具有多孔介質層的雙擴散自然對流機理對于提升鹽池蓄熱能力是十分必要的。

中外學者對于多孔介質腔體的雙擴散自然對流展開了大量研究。Mondal等[7]在均勻和非均勻邊界條件下,分析了浮力比對多孔介質空腔雙擴散自然對流的影響,描繪了流體流動形態隨時間的變化。Lakshmi等[8]在局部熱不平衡狀態下,分析了矩形與圓柱形多孔介質腔體的雙擴散自然對流過程,獲得了最適用于蓄熱系統的腔體形狀。雷鳴[9]分析了兩種多孔介質Lattice Boltzmann模型,結果表明,兩種模型在穩態不可壓流動下均適用。李貝貝等[10]模擬研究了含有高濃度高溫圓的多孔介質空腔內雙擴散自然對流,探討了達西數和浮升力比對高溫圓表面傳熱傳質效率的影響。邵明芹等[11]模擬研究了多孔介質空腔的自然對流傳熱,獲得達西數、瑞利數等控制參數與傳熱效率的關聯式。張貝豪等[12]模擬分析了傾斜多孔介質腔體的自然對流傳熱,考慮多孔介質物性參數與空腔傾斜角等因素對傳熱效率的影響。

熵產最小化是一種新興的工程系統優化熱力學方法,其主要思想是將設計的熱力學非理想程度與系統的物理特性(如有限的尺寸、形狀、材料、有限的速度和操作間隔的有限時間)聯系起來,改變一個或多個物理特性,以優化設計,其特征是在有限尺寸和有限約束下的最小熵產。對于多孔介質腔體的熵產,中外學者已開展大量研究。Mchirgui等[13]分別對多孔介質腔體進行了模擬研究,結果發現降低達西數會增加熵產,而孔隙度對熵產有正面影響。Meshrama等[14]模擬研究了傾斜多孔介質腔體內多個控制參數對熵產的影響,結果表明:腔體傾斜角對熵產有重要影響。Siavashi等[15]模擬研究了傾斜多孔介質腔體內不同熱源對熵產的影響,并根據熱力學第二定律獲得了最佳熱源位置。Hussain等[16]對填充納米流體的多孔介質空腔進行了模擬研究,結果表明:納米流體的體積分數會促進熵產的產生。Hayat等[17]采用一種改進的達西定律模擬多孔介質腔體的流體流動,考慮了多個控制參數對流動不可逆性與熱不可逆性的影響。

近年來,格子Boltzmann方法(lattice boltzmann method,LBM)作為一種介觀動力學方法,已發展成為模擬復雜多尺度流動的有力數值工具[18-20]。與有限容積法等傳統數值模擬方法相比,LBM不需要處理Navier-Stokes方程中的壓力項,計算時間更短。特別是,LBM更容易進行并行計算,在高性能計算機中運行更高效。目前大多數研究僅局限于純多孔介質腔體,對于部分填充多孔介質的內產熱腔體討論較少。為此,針對鹽梯度太陽池,研究多孔介質層對鹽池內部雙擴散自然對流的影響。將鹽梯度太陽池簡化為具有多孔介質層的內產熱腔體,同時考慮Soret和Dufour效應,采用LBM進行數值模擬。探討不同內熱源強度(R)、達西數(Da)、Soret(Sr)和Dufour(Du)效應作用下流體流動、溫度分布與濃度分布,并獲得了控制參數對傳熱傳質效率與熵產的作用機理與影響規律,理解多孔介質層對鹽梯度太陽池的熱鹽對流特性的影響,為提升鹽池蓄熱能力和長期運行穩定性提供理論依據。

1 LBM控制方程

采用不可壓格子BGK(Bhatnagar-Gross-Krook)模型,利用3個分布函數fk、gk與hk來模擬研究流場、溫度場與濃度場,對應分布函數分別表示為

(1)

(2)

(3)

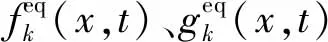
(4)

(5)

(6)

式中:ρ為流體密度;ε為多孔介質的孔隙率;U=(u,v),其中,u和v分別為速度在x和y方向上的分量;T(x,t)和S(x,t)分別為t時刻x點的溫度和濃度;ωk為權重系數;T和S分別為宏觀量溫度和濃度。

采用D2Q9模型,權重系數ωk和離散速度ck分別表示為

(7)

(8)

考慮多孔介質的力項Fk表達式為

(9)

(10)

G=g(βTΔθ+βSΔs)

(11)

式中:F為考慮多孔介質的外力項;G為浮力項;k為9個方向;c為格子速度;K為多孔介質的滲透率;βT和βS分別為熱膨脹系數和質膨脹系數;Δθ和Δs分別為溫差和濃度差。

因此,宏觀的流體密度ρ、速度v、溫度T與濃度S分別表示為

(12)

(13)

(14)

(15)

式中:T和S分別為宏觀量溫度和濃度;ΦT和ΦS為溫度源項和濃度源項。

考慮Soret、Dufour效應與內產熱的源項ΦT、ΦS分別表示為

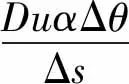
(16)

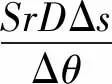
(17)

式中:Du和Sr分別為Dufour效應和Soret效應參數;α和D分別為熱擴散系數和質擴散系數;Ti,j和Si,j分別為位置(i,j)上的溫度和濃度。

2 模型描述與程序驗證

2.1 模型描述

如圖1所示,以鹽梯度太陽池的熱鹽對流現象抽象以下模型:將鹽池簡化為高寬比為0.5的內產熱矩形腔體。腔體由流體層與多孔介質層組成。其中,流體層具有強度為Q的內熱源,多孔介質層厚度為d。腔體底面為高溫高濃度(Th,Sh),上壁面為低溫低濃度(Tc,Sc),垂直壁面均為絕熱且不可滲透。

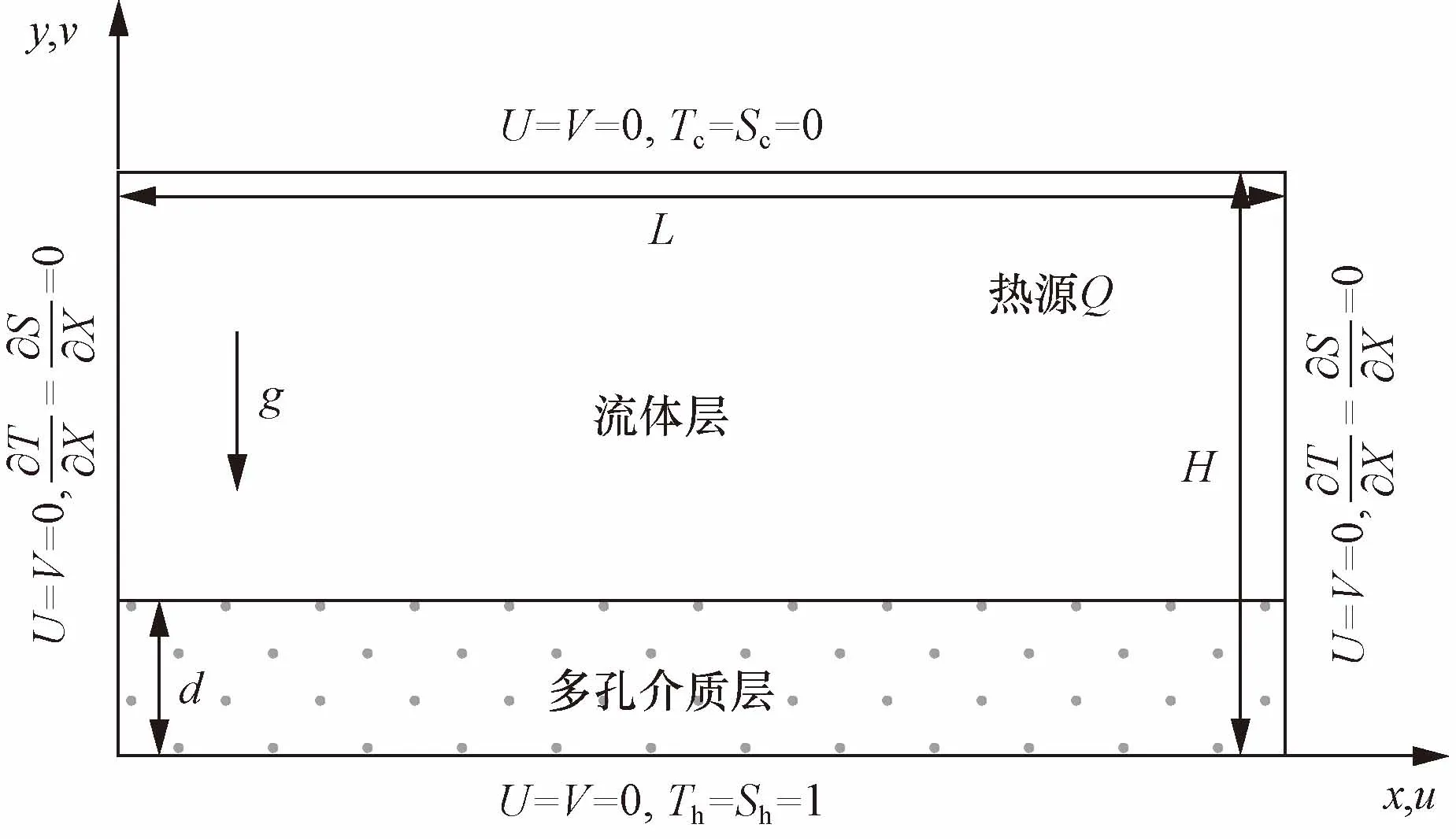
圖1 物理模型示意圖Fig.1 Schematic diagram of studied configuration

圖1中,腔體的高寬比為H/L,多孔介質層的厚度為d,流體層厚度為H-d,其中包含強度為Q的熱源。腔體的底面溫度(Th)和濃度(Sh)較高,頂面溫度(Tc)和濃度(Sc)較低,并且垂直壁面均為絕熱絕質壁面,可表示為

Y=0,U=V=0,Th=1,Sh=1

(18)

(19)

(20)

采用底面的平均努塞爾數(Nu)和舍伍德數(Sh)來評估該腔體的傳熱傳質效率,其表達式分別為

(21)

(22)

局部熵產(SL)由流動不可逆性(SF)、熱不可逆性(SH)和質不可逆性(SD)組成,其表達式分別為

SL=SF+SH+SD

(23)

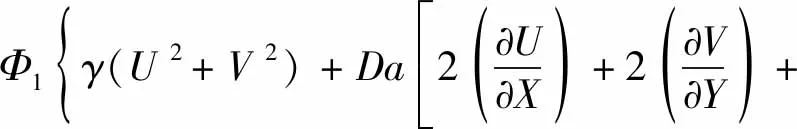
(24)

(25)

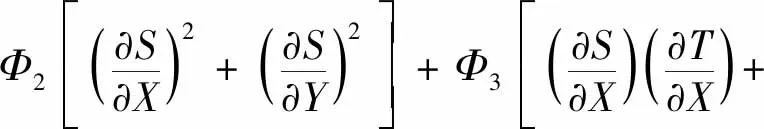
(26)

式中:γ用來區分多孔介質層與流體層,即γ=1對應多孔介質層,γ=0對應流體層;不可逆比Φ1、Φ2、Φ3分別取0.01、0.5和0.01[19-20]。

由此可得,總熵產(STL)與Bejan數(Be)分別表示為

(27)

(28)

2.2 網格獨立性與程序驗證

在R=0、Da=10-3、Sr=Du=0條件下,選取5種均勻網格100×50、120×60、160×80、200×100與300×150進行網格獨立性分析。如圖2所示,當網格為200×100時,平均努塞爾數(Nu)與舍伍德數(Sh)的數值不再隨網格的增大而變化,此時可視為網格無關性。因此,選用200×100的均勻網格。

微流控芯片的整體結構如圖1所示,包括PCB板、集成陣列電極的微流道及接口等。芯片通道入口選用“Y”型,方便不同種類細胞的混合和分離。芯片主通道上分布3個多電極陣列截面,用于主通道內部的電阻抗成像檢測。PCB板中印刷了芯片所需的電路,電極通過分布在PCB板兩側的插針接口與其他儀器進行信號傳輸,芯片的基板則通過螺釘和固定板固定在PCB板中。

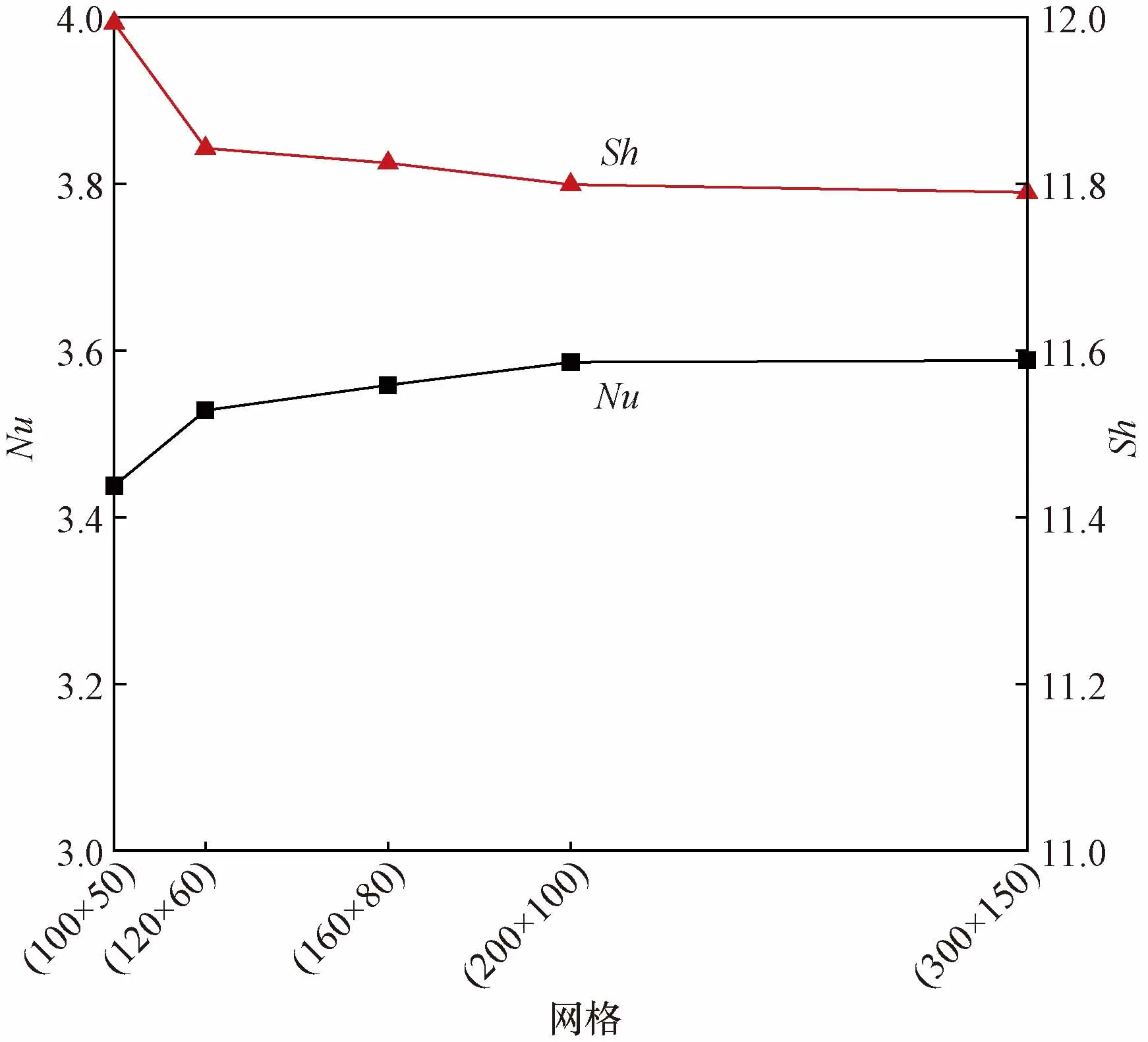
圖2 平均努塞爾數Nu和舍伍德數Sh的網格獨立性Fig.2 Grid independence of average Nusselt and Sherwood numbers

選取相似問題進行程序驗證。首先,本文程序與對Soret效應作用下的內產熱空腔進行對比驗證。如表1所示,誤差小于3%,所得結果與文獻[18]吻合良好。其次,本文程序與多孔介質方腔的熵產進行驗證,如表2所示,誤差小于4%,所得結果與文獻[13]吻合良好。

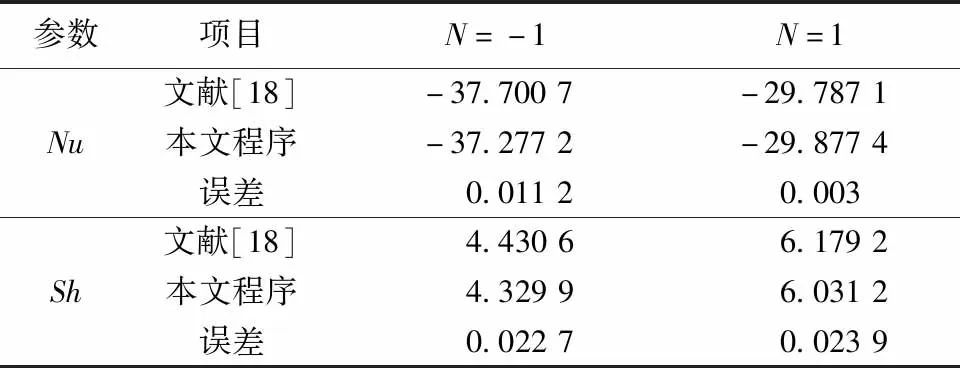
表1 Soret效應作用下內產熱方腔內不同浮升力比平均努塞爾數Nu和舍伍德數Sh驗證Table 1 Validation of average Nusselt and Sherwood numbers in an internal heating enclosure with Soret effect

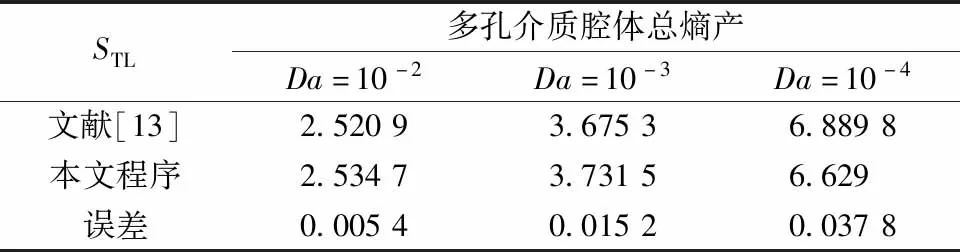
表2 不同Da數下多孔介質腔體總熵產驗證Table 2 Validation of total entropy generation inside a porous enclosure with various Da

3 結果與分析

3.1 傳熱傳質特性

內產熱強度對腔體內流動與傳熱傳質過程的影響如圖3所示。在圖3(a)中,此時腔體內無內產熱,腔體內部形成4個對稱的渦,包括兩個順時針與兩個逆時針流動,均位于流體層中。同時,多孔介質層內無流體流動,形成溫度與濃度邊界層,說明多孔介質層內傳熱方式以導熱為主。當內產熱強度增大時,如圖3(b)所示,腔體中心的溫度升高,這導致腔體中心的兩個渦逐漸增大,靠近垂直壁面的兩個渦逐漸減小。當內產熱強大繼續增大時,在圖3(c)中可明顯觀察到靠近垂直壁面的渦已消失腔體內形成兩個對稱流動方向相反的渦,腔體的整體溫度升高,最大溫度由底面遷移到了腔體中心。

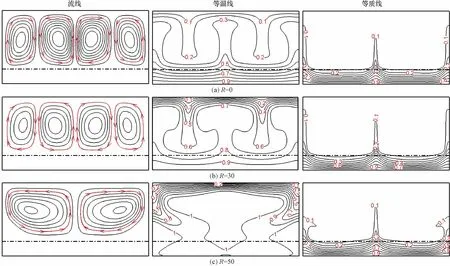
圖3 不同內熱源強度的流場、溫度場和濃度場圖Fig.3 Fluid flow,temperature and concentration fields with the variation of internal heat generation

達西數對腔體內流動與傳熱傳質過程的影響如圖4所示。當達西數較小時(Da<10-3),此時多孔介質引起的黏性阻力較大,多孔介質呈現固體的特性。由圖4可知,Da=10-5與Da=10-4的結果相似,腔體內形成4個均勻分布的渦,多孔介質層內部流體處于靜止狀態同時底面形成溫度邊界層與濃度邊界層。當Da增大至10-3,多孔介質引起的黏性阻力減小,多孔介質層內出現微弱的流動。此時,在流體層內產熱的作用下,腔體流體的流動強度增強,靠近垂直壁面的渦逐漸變小,流體流動的增強同時導致腔體中心的溫度與濃度逐漸增大。當Da增大到10-2時,此時多孔介質的黏性阻力可忽略不計,腔體內流動強度得到極大增強,這導致靠近壁面的渦消失,腔體內形成兩個對稱且流動方向相反的渦。腔體中心的溫度和濃度增大,說明Da的增加極大地增強了腔體內部的傳熱傳質過程。因此,多孔介質層對于腔體內的傳熱傳質過程有很好地抑制作用,但盲目減小達西數對結果的影響并不大。

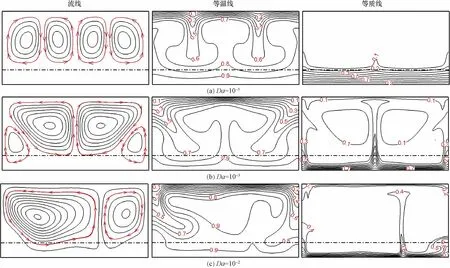
圖4 不同達西數的流場、溫度場和濃度場圖Fig.4 Fluid flow,temperature and concentration fields with the variation of Darcy number

達西數Da與內產熱強度R對平均努塞爾數Nu和舍伍德數Sh的聯合影響如圖5所示。由圖5可知,Nu與Sh均隨Da的減小而減小,并且在低達西數(Da<10-3)的工況下,Nu與Sh幾乎不在變化。這說明多孔介質層對于腔體底面傳熱傳質過程具有良好的抑制作用。在低達西數(Da<10-3)的工況下,隨R變化的Nu曲線呈現單調遞減的趨勢,而Sh曲線基本保持不變。Da=10-4時,R由0增大到50對應的Nu減小了90%,而Sh的變化小于5%。這是由于腔體的溫度受到內產熱作用會逐漸增大,且最大溫度會由底面向中心位置遷移,這導致底面的傳熱效率減小。同時,低達西數的多孔介質黏性阻力較大,底面形成穩定的質邊界層,因此Sh幾乎不受R的影響。在高達西數(Da>10-4)的工況下,隨R變化的Nu與Sh曲線均呈現單調遞減的趨勢。Da=10-2時,Nu與Sh分別減小了77%與22%。這是由于高達西數時,腔體內流體流動強度增強,內產熱的增強使得底面傳熱傳質效率均減小。

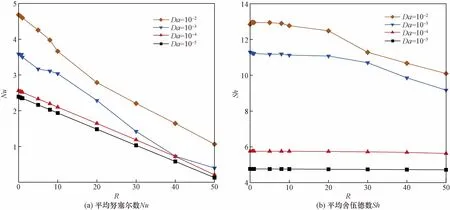
圖5 不同達西數下平均努塞爾數Nu與舍伍德數Sh隨內產熱系數的變化規律Fig.5 Average Nusselt and Sherwood numbers with varying internal heat generation for different Darcy number

Soret與Dufour效應對腔體傳熱傳質過程的影響如圖6、圖7所示。由圖6可知,隨著Sr的增加,濃度場有顯著變化。當Sr=0.2時,Soret效應較小對腔體內的流動與傳熱傳質影響較小,流場、溫度場與濃度場均沒有顯著變化。當Sr增大到0.8時,多孔介質層內的質邊界層被破壞,等質線從底面逐漸向腔體中心遷移,腔體中心的濃度上升。特別是Sr增大到1時,腔體中心濃度繼續上升,且更多的等質線集中在腔體中心。這說明Soret效應對腔體的傳質過程有極大的促進作用,但對傳熱過程沒有顯著影響。由圖7可知,隨著Du的增大,腔體的整體溫度升高并且渦面積變大,腔體的最高溫度逐漸高于底面溫度。這意味著Dufour效應促進了內產熱對腔體溫度的升高,從而增強了腔體內流體的流動強度與傳熱過程。對比可知,在內產熱腔體內Dufour效應的作用大于Soret效應。

圖6 不同Soret效應的流場、溫度場和濃度場圖Fig.6 Fluid flow,temperature and concentration fields with the variation of Soret effect

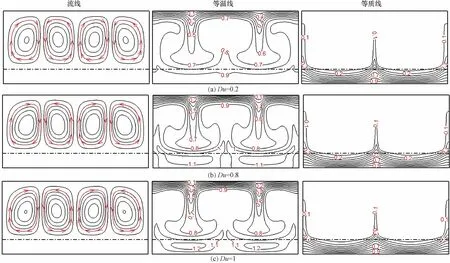
圖7 不同Dufour效應的流場、溫度場和濃度場Fig.7 Fluid flow,temperature and concentration fields with the variation of Dufour effect

Soret與Dufour效應對平均努塞爾數與舍伍德數的影響分別如圖8、圖9所示。圖8中,隨著Sr的增加,Nu幾乎保持不變,并且Sh呈單調遞增的趨勢。這說明,Soret效應只對傳質效率有促進影響,而對傳熱效率無明顯影響。隨著R的增加,Sh曲線呈單調遞減趨勢,最終在R=50時重合。這是由于R增加,內產熱產生的熱浮升力與質浮升力產生對抗作用,從而抑制了Soret效應對傳質效率的促進作用。由圖9所示,隨著Du的增加,Nu不斷增大,Sh幾乎保持不變。這說明Du只對腔體底面的傳熱效率有促進作用,對傳質效率無顯著影響。另外,在Du=0時,Nu隨R的變化曲線為單調遞減的。然而,隨著Du的增加,Nu曲線的變化趨勢發生改變,并且在Du>0.5的工況時,Nu曲線呈單調遞增的趨勢。這是由于Dufour效應極大地增大了底面傳熱效率,并且在Du>0.5時,Dufour效應的增強作用大于內產熱的抑制作用,此時的Nu隨R的增加而增大。因此,在這個鹽梯度太陽池抽象的腔體內,Soret與Dufour效應對流動與傳熱傳質過程的影響是顯著且不可忽視的。

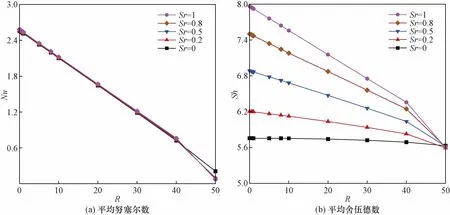
圖8 不同Soret效應、平均努塞爾數與舍伍德數隨內產熱系數的變化規律Fig.8 Average Nusselt and Sherwood numbers with varying internal heat generation for different Soret effect

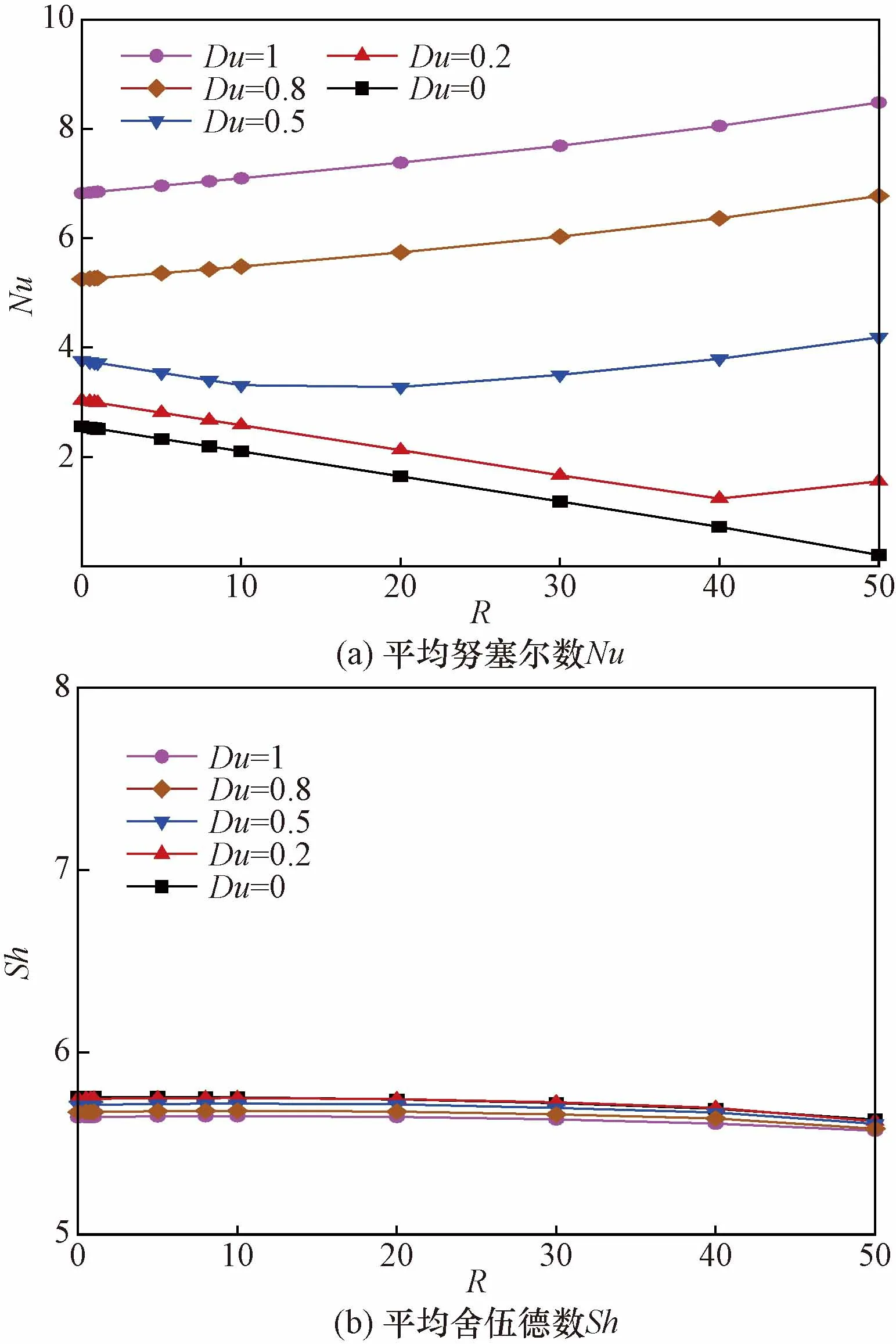
圖9 不同Dufour效應,平均努塞爾數與舍伍德數隨內產熱系數的變化規律Fig.9 Average Nusselt and Sherwood numbers with varying internal heat generation for different Dufour effect

3.2 熵產分析

達西數與內產熱強度對腔體總熵產與Be的聯合影響如圖10所示。可以看出,STL與Be隨R增加的變化曲線呈單調遞增的趨勢。這是由于R的增加導致熱不可逆性極大地增加,并且在R>30時,熱不可逆性遠大于流動不可逆性與質不可逆性,從而Be超過0.5。另外,可觀察到Da的增加會導致STL的增大。這是由于高達西數(Da>10-4)會促進了流動與傳熱傳質過程,從而高達西數的多孔介質層會產生較大的熵產。同時,Da的增加導致Be的減小,并且在Da=10-3時Be達到最小值。這是由于Da的增加導致多孔介質層內的流體流動極大地增強,此時熱不可逆性的占比減小。但當Da增加到10-2時,熱不可逆性的占比增加,從而Be增大。因此可知,多孔介質層對熵產最小化有積極的作用。

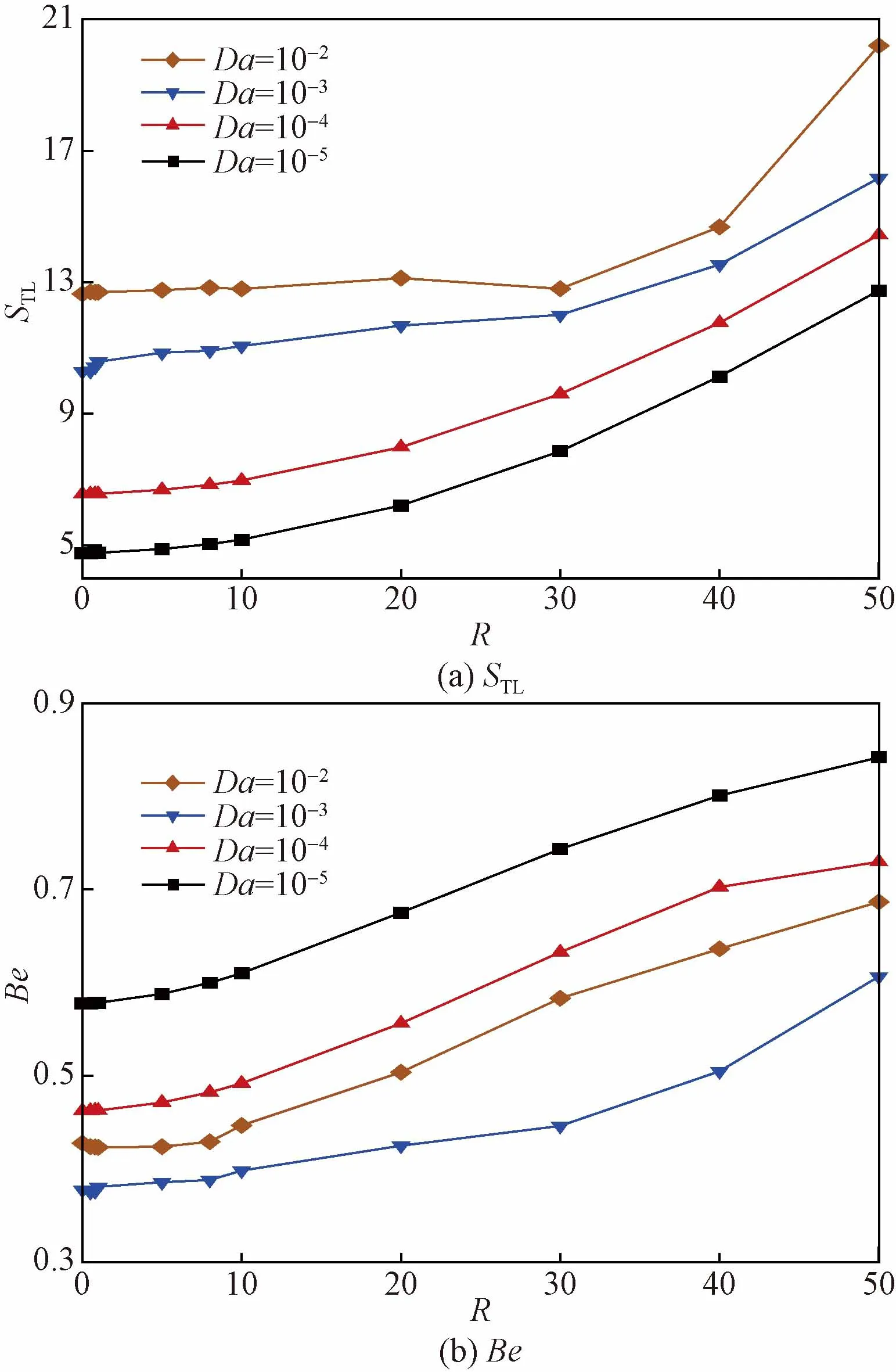
圖10 不同達西數,總熵產與Bejan數隨內產熱系數的變化規律Fig.10 Total entropy generation and Bejan number with varying internal heat generation for different Darcy number

Soret與Dufour效應對腔體總熵產與Bejan數的影響分別如圖11、圖12所示。在圖11中,隨著Sr的增加,R<30的范圍內STL沒有顯著影響且Be略有增加。這是由于Soret效應對傳質過程有促進作用,導致質不可逆性增加,而流動不可逆性減小。

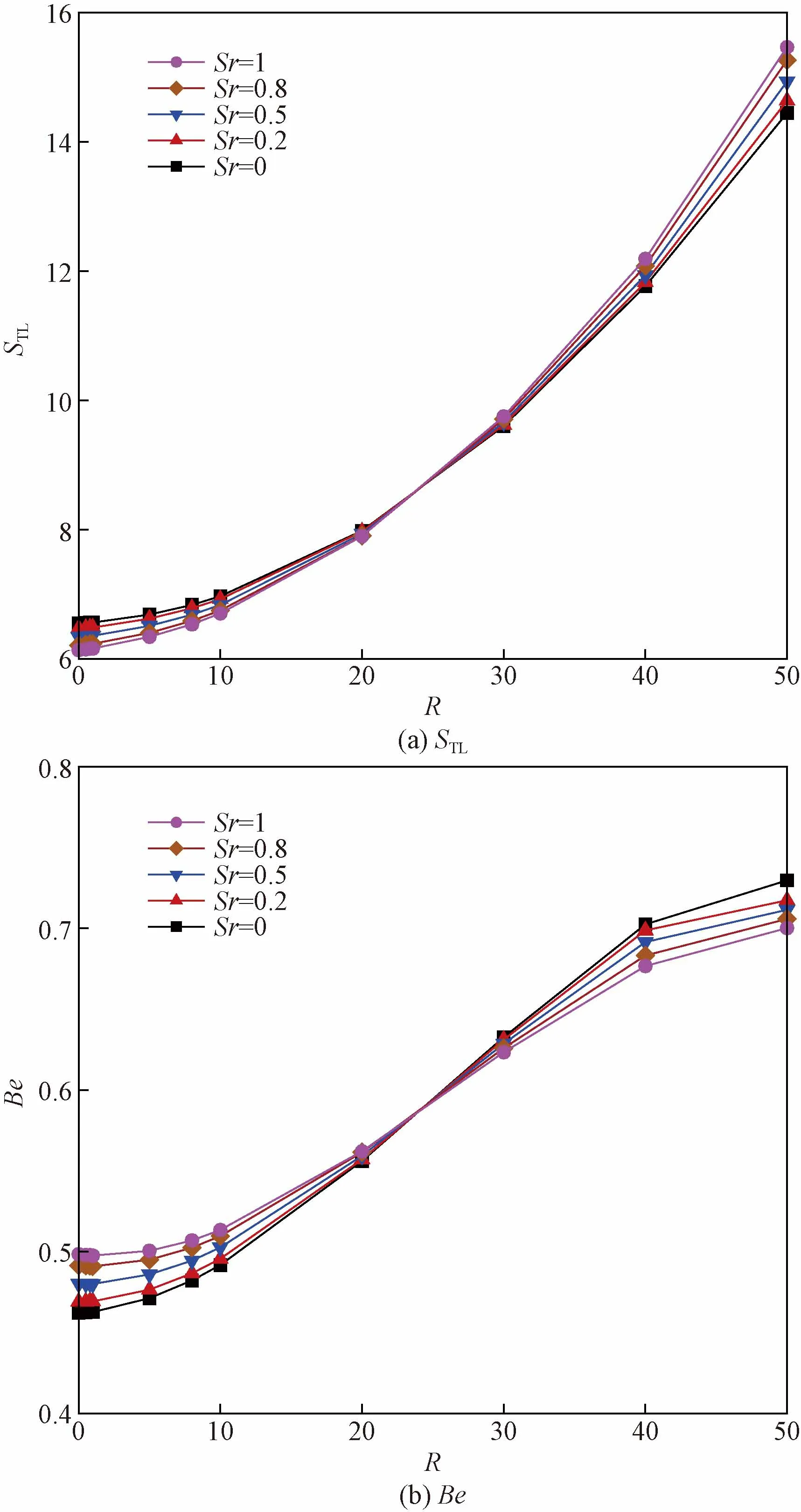
圖11 不同Soret效應,總熵產與Bejan數隨內產熱系數的變化規律Fig.11 Total entropy generation and Bejan number with varying internal heat generation for different Soret effect

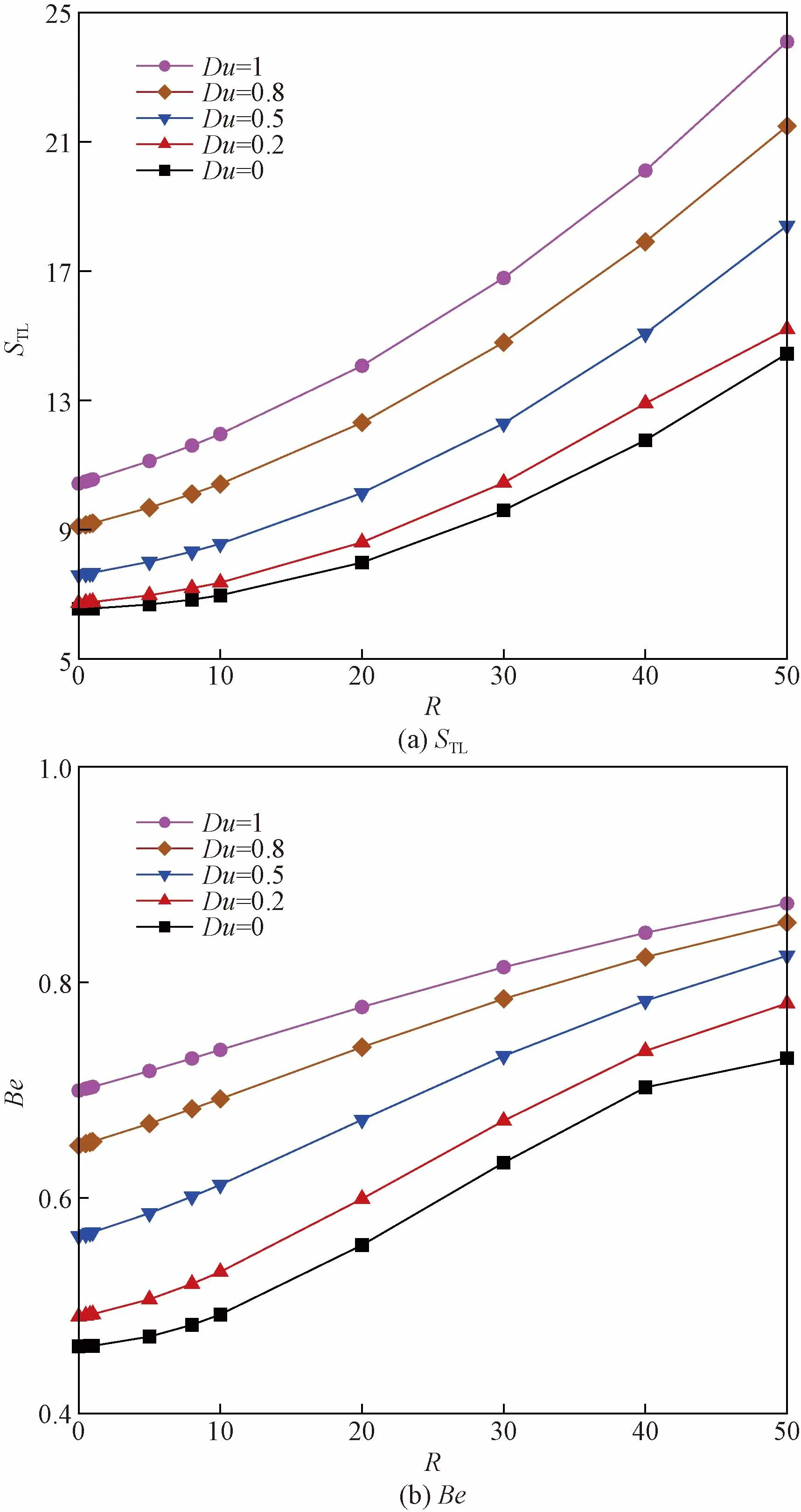
圖12 不同Dufour效應,總熵產與Bejan數隨內產熱系數的變化Fig.12 Total entropy generation and Bejan number with varying internal heat generation for different Dufour effect

而R>30的范圍內,STL出現增大而Be減小的趨勢。這是由于隨著R增加,內產熱產生的熱浮升力與質浮升力產生對抗作用,腔體內的傳質過程被抑制,質不可逆性減小而流動不可逆性增加,此時,在Soret效應作用下總熵產增大而Bejan數減小。另一方面,如圖12所示,Dufour效應極大增加了總熵產與Bejan數,且在Du>0.5時,Be遠大于0.5。這是由于Dufour效應對流體腔體內的流動與傳熱過程有顯著的影響,流動不可逆性與熱不可逆性得到極大地增加,并且在Du>0.5時,熱不可逆性的增加遠大于流動不可逆性,從而Bejan數不論R為多少都遠大于0.5。同時,Dufour效應促進了內產熱對傳熱過程的積極作用,從而R越大,STL曲線的增加幅度越大。在R分別為30和50的工況下,Du從0增大到1時,STL分別增加了40%和42%。由圖11、圖12可知,由于內產熱的存在,熱不可逆性在總熵產的占比遠超于質不可逆性與流動不可逆性,因此Soret效應對熵產的影響較小,而Dufour效應的影響較大且不可忽略。

4 結論

(1)多孔介質層對腔體內部傳熱傳質過程有很好地抑制作用,低達西數(Da<10-3)可減小腔體底面的傳熱傳質效率。多孔介質層對熵產最小化有積極作用,低達西數有助于抑制熵產的產生。內產熱強度對熵產有促進作用,總熵產隨內產熱強度的增強而增加,并且在高內產熱強度(R>30)的工況下,Bejan數高于0.5,熱不可逆性處于主導地位。

(2)Soret與Dufour效應對腔體內部的傳熱傳質過程有顯著的影響。增強Dufour效應會促進內產熱對腔體內部傳熱過程的積極作用,故高Dufour效應(Du>0.5)工況下,傳熱效率隨內產熱強度的變化呈單調遞增趨勢。Dufour效應對熵產有顯著的影響,而Soret效應作用不明顯。高Dufour效應(Du>0.5)的工況下,Bejan數遠高于0.5,熱不可逆性在總熵產的占比遠超于質不可逆性與流動不可逆性。