基于AGREE法的鑄造起重機起升機構可靠性分配

郭志敏 張宇鵬

1 中國寶武太鋼集團熱連軋廠 太原 030001 2 太原科技大學機械工程學院 太原 030024

0 引言

鑄造起重機是鑄造行業專用的起重機，主要負責煉鋼車間中鋼包的吊運和澆鑄，工作環境溫度高，灰塵大。由于鑄造起重機特殊的吊運作業和惡劣的工作環境，若發生事故會造成重大經濟損失和社會影響，因而任何噸位的機型都有極高地工作級別，故鑄造起重機的安全性和可靠性要求極高。起升機構是鑄造起重機的核心機構，負責液態熔融金屬的轉運和傾倒工作，在吊運時需承受爐口上方100℃以上的高溫。因此，對起升機構進行可靠性分配，對關鍵的零部件重點維護，可極大地提高鑄造起重機工作的安全性，減少安全事故的發生概率。

對鑄造起重機起升機構的可靠性分析，許多學者進行了大量的研究工作。李銳鵬等[1]總結了鑄造起重機起升機構機型的演變和發展，從可靠性、安全性、易維護性等方面分析了每種布置結構的優缺點；郝建光[2]對起升機構實例進行系統可靠性分析，對比有無安全制動器的設計對起升機構的整體可靠差異；李卓[3]針對鑄造起重機起升機構的不同工況建立考慮人、機、環境交互的安全評估評價體系，為鑄造起重機起升機構的安全研究提供理論支撐；陸鳳儀等[4]采用T-S 模糊故障樹對鑄造起重機起升機構的可靠性進行分析，得到起升機構半故障、完全故障的失效概率。

在當前工程實際中，常用的可靠性分配方法包括等分配法、最小成本法、失效率比例分配法[5]、綜合因子分配法[6]、考慮重要度和復雜度的分配法(AGREE)[7]、權衡費用的分配法[8，9]層次分析法[10，11]等。電子產品由于其零部件具有通用化、成本低廉等優勢，一般通過冗余使用關鍵零部件的方法實現系統的可靠性指標。在電子產品中經常會有大量的冗余部件，在對系統進行可靠性分析時會出現復雜的故障狀態，傳統的可靠性分析方法對多狀態、多備件、存在順序失效的系統分析有難度，同時系統的復雜化對可靠性分配也會造成新的困難，備用件和工作部件的可靠性指標分配工作是否需要一致、在工作部件發生失效期間備用件的故障狀態是否可以確定等問題。

在機械裝備結構中，大型機械零部件的數量和復雜程度與電子產品不相上下，且在機械結構中不會有完全不工作的備用部件，故對每個零部件的可靠性要求極高。特種設備因其特有的工作區域和惡劣工作環境，且使用的非標產品大多根據其設計要求而定，缺乏大量有效故障數據，無法做到零部件低成本替換，惡劣的工作環境對冗余組件的故障影響不能忽略，結構限制也不允許通過大量冗余組件提高其可靠性，故只能從提高組成單元的可靠性方面來提高系統可靠度[12]。

針對上述不足，本文引入故障樹對鑄造起重機起升機構進行可靠性分析，并由重要度分析得到各組成機構的重要度，基于重要度對鑄造起重機起升機構進行可靠性再分配，得到鑄造起重機起升機構在故障樹下的可靠性分配，為鑄造起重機起升機構的維護，故障排查提供理論依據。

1 可靠性分配方法

1.1 可靠性分配理論

可靠性分配是指在系統總體的可靠性指標確定后，由頂事件自上而下的逐層可靠性指標分配給各子系統或零部件。通過對各子系統的可靠性進行合理分配，對提高整個系統的安全性和后期可靠性的優化具有重要意義。當前工程實際中常用的可靠性分配方法有等分配法、最小成本法、AGREE 法等，可靠性分配中最核心的難點是如何在現有條件約束下使系統獲得最大的可靠度[13]；解決問題主要針對系統的組成、工作模式、零部件危害度、重要度等方面，分析提高系統可靠度的難易程度。如圖1 所示，可靠性分配的基本流程包括：1）根據目標的要求，確定分析系統的可靠性指標；2）根據分析對象的結構組成，確定分配的底事件；3）選取合適的可靠性分配方法；4）建立可靠性分配模型；5）得到分配給子系統和零部件的可靠度，進行驗算是否達到系統的可靠性指標。

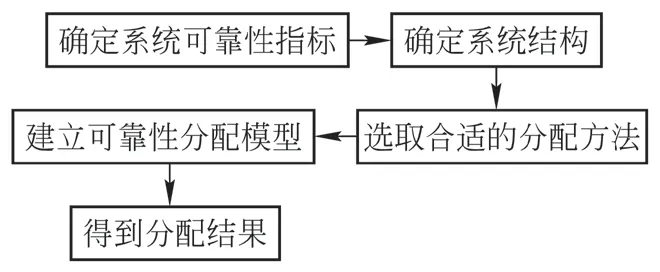
圖1 可靠性分配流程圖

1.2 可靠性分配方法

1）等分配法

等分配法是一種快速且便捷的可靠性分配方法，該方法不考慮子系統零部件的復雜度和重要程度，默認其可靠性水平相當。將設定的可靠性指標按照部件數量平均分給每個零部件，雖然計算簡單省時，但在分配過程考慮的因素不足，分配結果不具參考價值。

2）層次分析分配法

該方法的分配原理是在分析之前對分析目標進行層次劃分，綜合考量專家對不同影響系數和子系統零部件的關鍵程度的評判指標，確定不同零部件之間的可靠性指標比例關系，最終得到分配結果。層次分析法對于系統的設計者來說，可以很輕松地進行分配，較貼近實際，但要求分配者對系統結構的認知度較高。

3）比例組合分配法

該方法實際是借鑒相似系統或系列產品現有的分配結果，與分配系統進行類比可直接得到分配結果。然而對于開發新系統或無類似系統時，該方法卻無法使用。

4）AGREE 分配法

該方法是20 世紀美國提出的分配方法，其綜合考慮了部件的工作時間、重要度、復雜度等影響系統可靠性的因素，適用于零部件壽命服從指數分布的串聯系統的可靠性分配。

2 重要度計算

重要度是描述底事件發生概率對于故障樹頂事件發生概率的影響程度，代表零部件失效對整個系統失效的貢獻指標。重要度的研究最早起源于20 世紀，是為了確定組成系統的零部件的關鍵程度、找到系統的薄弱環節而提出的。隨著系統的功能、結構不斷發展豐富，對各種重要度的研究也越來越多元化，針對底事件故障率變化、故障狀態的不同，得出不同的重要度，從不同角度得到系統的薄弱環節。重要度在針對系統的可靠性再分配、故障診斷、安全評估、系統的改進優化等方面起著重要作用。常見的重要度有概率重要度、結構重要度、關鍵重要度等。

2.1 概率重要度

系統概率重要度的定義為：當只有第i個零部件由正常狀態變化為故障狀態時，頂事件發生概率的變化率反映底事件狀態變化對于系統整體故障率的影響，概率重要度的計算方法是取底事件i故障狀態1 時系統故障率減去該事件故障狀態為0 時系統的故障率。底事件xi的概率重要度IPr（xi）為

式中：P（T，1i）為底事件xi故障時頂事件的故障率，P（T，0i） 為底事件xi故障時頂事件的故障率。

2.2 結構重要度

結構重要度即底事件的故障狀態從0 到1 時系統頂事件發生概率的變化，是指在不考慮各底事件發生概率不同的情況下，從動態故障樹結構上對底事件的重要程度進行分析，底事件結構重要度等于所有底事件故障概率均為0.5 時該部件的概率重要度。

本文利用最小割集法底事件xi的結構重要度判斷基本事件的重要度排序，可近似求解得到基本事件結構的近似值為

式中：Xi為第i個基本事件；Kj為最小割集，j＝1，2，…，m；m為最小割集的個數；J（i）為基本事件Xi的重要度近似值；ni為基本事件Xi所在最小割集的階數。

3 AGREE 分配法

AGREE 法是由20 世紀美國為了降低武器裝備的失效率提出的經典方法。該方法充分考慮了零部件重要度、復雜度、工作時間等影響因素，適用于零部件單元壽命服從指數分布的串聯系。傳統AGREE 分配法的計算方法為

式中：Rs為系統可靠度，ωi為子系統i的重要度影響因子，θi為子系統i的平均無故障時間，ni為子系統i包含的單元數，N為系統包含的單元數。

對式（3）兩邊取對數，可進一步得到第i個子系統的平均無故障時間θi為

進而得到子系統i的可靠度Ri為

由式（5）可得，子系統分配的可靠度指標與其重要度之間的關系密切，重要度越高子系統分配的可靠度指標就越高；子系統復雜度因子越大，計算得到的無故障時間越短，重要度越低。

3.1 子系統復雜度Ii

子系統的復雜度定義為：組成子系統的零部件占整個系統組成部件的數量比值，在不考慮子系統失效相關的假設下，子系統i的重要度Ii為

式中：n為組成系統的子系統部件，ni為子系統i包含零部件個數。

3.2 子系統重要度因子

利用FTA 中的最小割集計算基本事件的重要度，再利用下行法分析故障樹，得到最小割集Qi，i為最小割集的個數。根據計算每個底事件Xi的結構重要度Ji，而子系統Si的結構重要度ωi是其所包含集合內的所有底事件的結構重要度之和，即

4 實例分析

以某鑄造起重機起升機構為例，其機構布置如圖2所示。該起升機構由2 臺電動機驅動同1 臺行星減速器、采用單減速器雙卷筒的布置形式，行星減速器的2 個輸出端各連接1 個卷筒，鋼絲繩從雙卷筒連接到起重橫梁上，橫梁連接吊具進行鋼包的吊運。該起升機構具有獨特的布置形式，在1 套電動機或卷筒發生故障時，另一套仍可以額定運轉速度的一半保持安全運行。起升機構根據其結構分為驅動系統、制動系統、傳動系統、卷繞系統4 個子系統，具體工作參數如表1 所示。

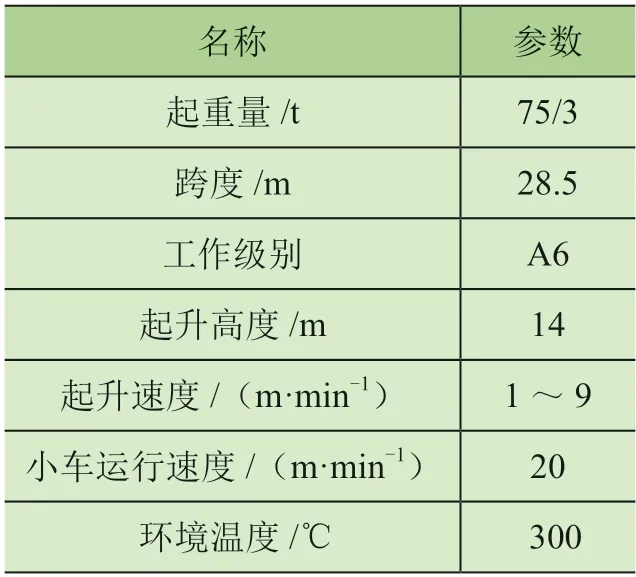
表1 鑄造起重機主要技術參數

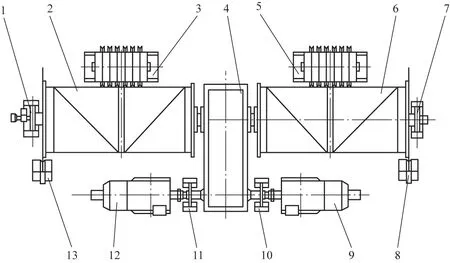
圖2 鑄造起重機起升機構布置圖

假設系統可靠性指標為0.99（1 000 h），分別計算出各子系統的可靠性指標。根據該起升機構布置形式和失效特點分析，構造鑄造起重機起升機構故障樹如圖3所示。在圖3 中，起升機構故障可分為驅動系統故障、傳動系統故障、制動系統故障和卷繞系統故障，每個故障均會導致鑄造起重機無法繼續工作，制動機構故障包括工作制動器故障和安全制動器故障，只有當2 組制動機構全部發生故障時起升機構才會完全不發工作。

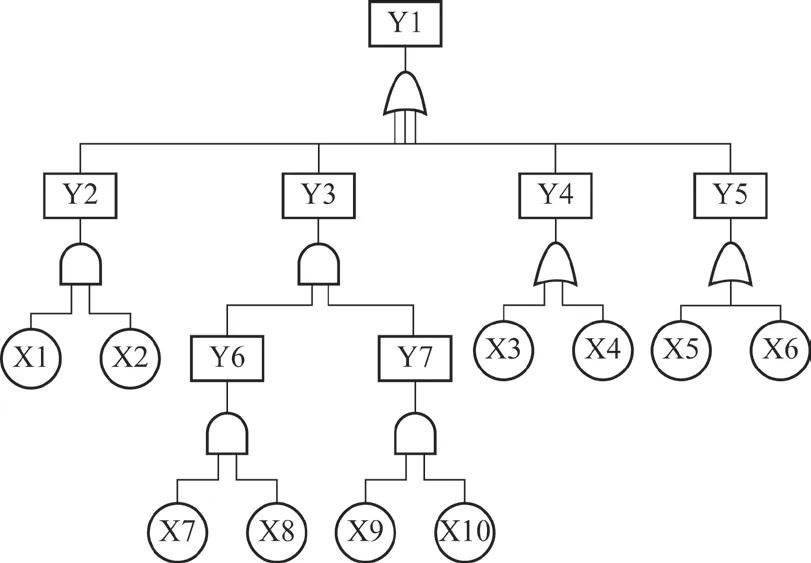
圖3 鑄造起重機起升機構故障樹

在圖3 中，Y1 表示起升機構故障，Y2 表示驅動系統故障，Y3 表示制動系統故障，Y4 表示傳動系統故障，Y5 表示卷繞系統故障，Y6 表示工作制動器故障，Y7表示安全制動器故障，X1 表示電動機1 故障，X2 電動機2 故障，X3 表示減速器故障，X4 表示聯軸器故障，X5 表示鋼絲繩故障，X6 表示吊鉤組故障，X7 表示工作制動器1 故障，X8 表示工作制動器2 故障，X9 表示安全制動器1 故障，X10 表示安全制動器2 故障。由此，可以得到每個子系統的底事件集和為：

底事件X1、X2 屬于驅動系統，即Q1＝{X1，X2}

底事件X7 ～X10 屬于制動系統,即Q2＝{X7，X8，X9，X10}

底事件X3、X4 屬于傳動系統，即Q3＝{X3，X4}

底事件X5、X6 屬于起升系統，即Q4＝{X5，X6}

由下行法得到鑄造起重機故障樹的最小割集為{X1，X2}、{X7，X8，X9，X10}、{X3}、{X4}、{X5}、{X6}，根據式(2)計算出每個底事件的重要度如表2 所示。

表2 底事件重要度

根據式（7）計算每個子系統的復雜度系數為：ω1＝0.667，ω2＝0.572，ω3＝2，ω4＝2。根據式(6)計算每個子系統的復雜度分別為CP1＝0.2 ，CP2＝0.4，CP3＝0.2，CP4＝0.2。根據式（4）、式（5）計算得到R1＝0.996 9，R2＝0.992 9，R3＝0.998 9，R4＝0.998 9。根據每個子系統分配得到的可靠性指標，計算得到鑄造起重機起升機構可靠性分配結果如表3 所示。

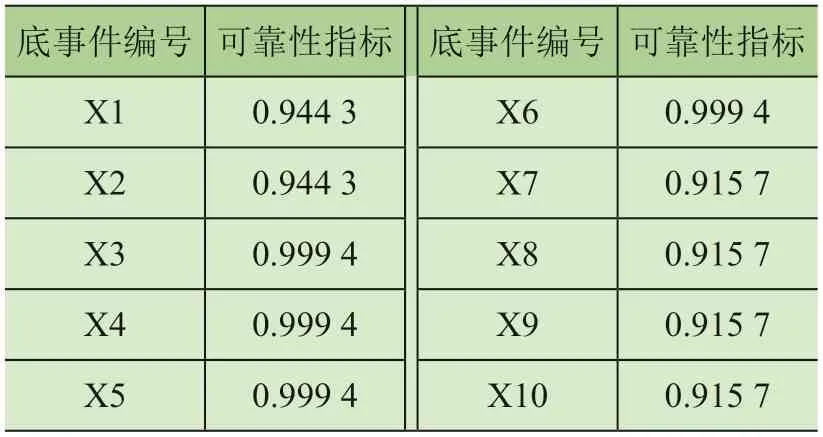
表3 底事件可靠性指標

5 結論

本文通過故障樹和AGREE 法對鑄造起重機起升機構進行可靠性分配，引入故障樹的結構重要度，根據鑄造起重機失效機理和布置形式進行故障樹分析，確定其底事件結構重要度以及分系統零部件個數確定事件的復雜度，完成對鑄造起重機可靠性分配。由分析結果表明，傳動機構的卷繞系統分配到的可靠性較高，而有均載部件的制動系統和驅動系統分配到的可靠性指標較低，說明多冗余部件的設計可有效提高系統的可靠度。