某型雙機身飛機水上迫降數值模擬

孫肖元, 鄧楓, 劉學強

(南京航空航天大學 航空學院 飛行器先進設計技術國防重點學科實驗室, 江蘇 南京 210016)

0 引言

隨著跨水域飛行航線日益增加,飛機在飛行過程中遇到緊急情況需要水上迫降的可能性隨之提高。因此,關于飛機水上迫降和入水沖擊等跨介質過程的研究需要加以重視。通常,針對入水砰擊問題的研究方法主要分為理論研究、試驗研究和數值模擬研究。

在理論研究方面,關于入水沖擊的研究最早可以追溯到1929年,von Karman[1]做了水上飛機降落時的入水砰擊載荷研究。其利用動量守恒定律將飛機入水砰擊過程理想化,成為一個二維楔形體的入水砰擊過程,由此提出了關于物體入水砰擊的流體理論,得出了最早的關于砰擊載荷研究的理論。Wagner[2]引入了勢流理論的原理,并由此提出了將楔形體等效成一個擴展的平板結構,通過求解流體的速度勢方程,再利用伯努利方程得出砰擊載荷在平板表面的分布情況。Verhagen[3]利用板邊緣處的射流效應對壓力的分布進行了一定程度的光順處理,從而能夠計算出板邊緣處的壓力分布情況。Peseux等[4]采用三維Wagner理論和有限元方法,分析了圓錐體砰擊問題。Greenhow[5]討論了剛性物體的噴濺根部壓強問題。Zhao等[6]給出了一般形狀物體入水砰擊的計算方法。閆發鎖等[7]以Wagner的入水砰擊理論為基礎,提出了楔形體砰擊壓力的計算方法,并且通過相關實驗的對比驗證,得出了完整的壓力計算方法。

在實驗研究方面,Bocquet[8]利用圓形鋁板做了打水漂實驗,分別研究了速度、姿態角和入水角對水漂實驗的影響。Takagi等[9]做了關于砰擊載荷影響的實驗研究,通過改變模型的底板傾斜角和厚度,來測量結構的應力和加速度等數值的變化。孫輝等[10]做了關于V型板入水的響應實驗,得到了結構體入水的加速度以及應力響應等實驗數據。劉暉[11]設計了不同剛度楔形體的入水砰擊實驗,主要研究剛度這一參數對入水砰擊時的影響。Mcbride等[12]進行了9種不同機身形狀等比例縮小模型的迫降實驗,測量了模型的水平速度、姿態角、質心高度的變化。Yettou等[13]研究了對稱三維楔形體的入水砰擊過程,其實驗結果可為入水砰擊數值模擬研究提供實驗數據。蒲錦華等[14]通過TEMA圖像運動分析軟件跟蹤判讀高速攝像結果,獲得了某型飛機模型迫降著水瞬間的運動狀態。駱寒冰等[15]采用落體入水模型研究了砰擊過程的砰擊壓力與結構動響應規律。

在數值模擬研究方面,陳震等[16]利用MSC-Dytran仿真軟件對二維楔形體入水問題進行了數值模擬研究,闡述了空氣墊和重力對砰擊時液面的變化和根部的噴射具有一定的影響。張曉波[17]應用大型有限元軟件LS-DYNA模擬了二維剛性體的入水砰擊過程,研究了剛性體的入水高度、殼的厚度、有無沙漏現象、罰函數的系數選擇和重力等因素對入水過程的影響。王建凱[18]采用ANSYS-Fluent流體分析軟件模擬了物體的入水砰擊過程,研究了模型剖面的壓力分布和監測點垂向作用力的數值變化,得出了相對運動最大的部位最易發生砰擊現象、砰擊壓力峰值與船體剖面形狀具有一定的關系的結論。陳光茂等[19]利用光滑粒子流體動力學(SPH)方法對二維楔形體進行了仿真數值模擬,并將豎直方向的速度變化與實驗數據進行了對比驗證。駱寒冰等[20]利用LS-DYNA軟件研究三維楔形體的入水砰擊問題,采用基于任意拉格朗日-歐拉(ALE)算法和罰函數的耦合算法對楔形體的入水砰擊過程進行了數值模擬計算。盧昱錦等[21]綜合利用流體體積(VOF)模型和整體動網格方法(GMM)對高速入水的三維平板數值模擬,并主要針對不同入水角度進行了數值模擬研究。陸召嚴[22]利用SPH方法對某型直升機縮比模型進行了俯仰角分別為6°、8°和10°的帶有水平速度的水上迫降過程數值模擬。屈秋林等[23]結合VOF方法和GMM方法研究了NACA-TN2929模型各部件在水上迫降過程中的作用,計算結果表明飛機迫降過程中氣動載荷的影響不可忽略。Yan等[24]利用SPH方法對三維圓盤水漂運動進行了數值模擬,其數值結果和理論分析結果為本文提供了算例驗證數據。趙蕓可等[25]采用6自由度(6DOF)模型和GMM方法成功模擬了某型飛機的迫降過程。李勐等[26]采用ALE方法對飛機非對稱水上迫降過程進行數值模擬,分析了不同初始滾轉角情況下飛機的運動響應與力學特性。田北晨等[27]采用VOF方法對跨介質飛行器觸水滑跳過程展開數值模擬研究,主要研究了入水速度與入水俯仰角度對滑跳過程的影響。

隨著計算機技術的發展,各式各樣的數值模擬方法已經被應用于跨介質飛行器入水砰擊問題的數值模擬研究。基于以上學者的研究,本文綜合運用URANS方法、VOF方法、動網格技術和6DOF模型對某型雙機身飛機的水上迫降過程進行數值模擬研究,重點研究飛機入水俯仰角度這一關鍵參數對該飛機水上迫降過程的影響機制,為飛機水上降落過程研究提供參考和技術支持。

1 數值計算方法

飛機水上迫降過程是一個復雜的物理過程,涉及固、液、氣三者之間的相互作用。飛機水上迫降過程的數值模擬方法主要包括流體力學基本控制方程及求解、VOF方法、動網格技術和6DOF模型等。流體力學基本控制方程解決復雜的湍流和多介質流動問題,VOF方法實現對自由液面的追蹤,動網格技術和6DOF模型模擬飛機水上迫降的運動過程。通過非定常計算的方式模擬飛機在水上迫降過程中的數值變化,通過控制變量法研究飛機俯仰角這一重要參數對飛機水上迫降過程數值的影響。本文采用計算流體力學(CFD)分析軟件Fluent進行數值計算,其求解流程圖如圖1所示。

圖1 數值模擬流程

1.1 流體力學控制方程

目前,CFD仿真計算都是基于流體力學基本控制方程,其控制方程包括3個基本方程:連續性方程、動量守恒方程和能量守恒方程。由于本文的數值計算不涉及傳熱問題,不考慮能量守恒方程。控制方程采用三維不可壓縮URANS方程,其中包括連續方程和動量守恒方程。流體流動的連續方程可以表示為

(1)

式中:u、v、w分別表示某一空間點上x軸、y軸、z軸方向的流速。流體流動的動量守恒方程表示為

(2)

(3)

(4)

式中:p為流體中的壓力;fx、fy、fz分別為x軸、y軸、z軸上的單位質量力;ρ為流體密度;μ為流體的動力黏度系數;μT表示標準k-ε兩方程模型求解的湍流渦旋黏度。

1.2 VOF方法

VOF方法是一種能夠及時捕捉并追蹤自由界面的方法,具有操作簡單、計算穩定和魯棒性優異等優點。該方法中,互不相容的流體共同使用一套動量方程,并通過引入相體積分數這一變量來實現對流體計算域內自由界面的追蹤。對于流場中的每個網格單元,相體積分數定義為目標流體的體積與網格單元體積的比值,通過計算每個網格上的相體積分數,實現對自由界面的追蹤。通過對自由界面的追蹤,可以將流場中的空氣和水兩種不同的介質清晰地展示出來,空氣的VOF分數為0,水的VOF分數為1,而VOF分數介于0和1之間則代表水和空氣兩種介質的交界處,并通過求解VOF函數的控制方程實現交界面的呈現,其表達式為

(5)

式中:F為VOF函數。如圖2所示,VOF方法通過求出整個計算域內每個網格單元的VOF分數,可以構建出水-空氣相位交界面。為加快數值計算的收斂速度和增強計算穩定性,本文采用SIMPLEC算法處理流場內的壓力-速度耦合。

圖2 相位交界面的呈現原理圖

1.3 動網格技術與6自由度模型

綜合運用動網格技術和6DOF模型實現飛機水上迫降過程的動態模擬。采用彈性光順法和結構重構法等動網格方法。6DOF運動求解器能夠解決基于平移和旋轉自由度的物體運動過程,通過監視目標物體的6DOF數值變化進行數值模擬研究。如圖3所示,一般物體在空間內具有6個DOF,即沿x、y、z3個直角坐標軸方向的平移自由度和繞x、y、z3個直角坐標軸方向的旋轉自由度,這6個空間自由度可以自由組合和分解,構成三維空間內的所有運動。

圖3 一般物體的空間6DOF

將目標物體的質量、質心位置和質心慣性張量等質量屬性與初始速度、初始角速度等運動狀態通過用戶自定義函數(UDF)編譯的方式完成輸入。進而通過6DOF求解器監測物體質心位置的變化來獲得物體的位移。每個時間段的位移變化量Δs除以時間變化量Δt為該時間段內的速度,每個時間段內速度變化量Δvj除以時間變化量Δt為該時間段內的垂向加速度。根據牛頓第二運動定律,水作用在物體上的垂直力可以通過求解以下公式得到:

(6)

(7)

Ftotal=Mg-Fw=Ma

(8)

式中:vj表示物體的垂向速度;s表示物體的垂向位移;a表示物體的垂向加速度;i表示瞬時位移或時間的先后順序;Ftotal表示物體受到的總垂向作用力;M表示物體的質量;g為重力加速度,g=9.81 m/s2;Fw表示水作用在物體上的垂向作用力。

2 數值模型與網格設置

2.1 網格劃分與邊界條件

計算模型為某型雙機身飛機,其雙機身設計增大了飛機的運輸質量。飛機長度L為5.0 m、寬度D為5.8 m、高度H為2.0 m,飛機的質量為365.122 kg,將飛機的質心位置移動至計算域的坐標原點。飛機水上迫降時抬高機頭一定角度滑翔迫降,飛機的三視圖如圖4所示。

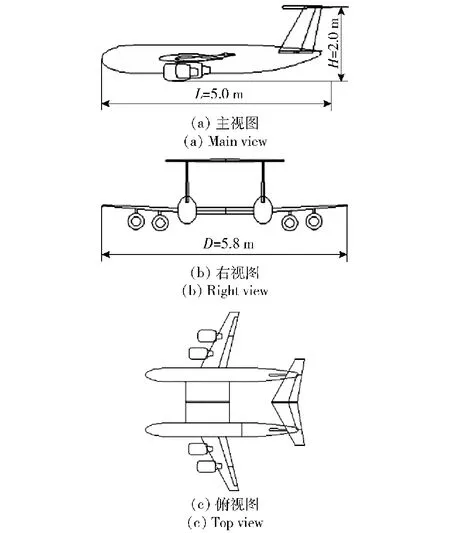
圖4 飛機三視圖

圖5為外流場計算域的邊界條件設置,計算域是一個10L×8L×5L的長方體,除計算域正上方的邊界條件是設置為pressure-outlet(壓力出口),剩余5面的邊界條件都設置為wall(壁面)。計算初始狀態時,飛機底部剛剛與水面接觸。

圖5 邊界條件

圖6展示了計算域內的網格劃分情況。為實現彈性光順模型和結構重構模型等動網格方法,計算域內全部采用四面體類型網格。在飛機的周圍生成一個球體移動網格區域,并對該區域的網格進行加密,便于準確地模擬飛機運動過程的數值變化以及更精確地捕捉飛機入水時周圍的水花現象。將飛機設置為剛性移動物體,周圍的球體移動網格區域設置為被動剛性移動區域,該區域在重力的作用下跟隨飛機一起移動,與飛機有相同的運動狀態,且內部網格不發生重構。

圖6 整體網格區域和移動網格區域

考慮到外流場計算域內的初始壓強分布對于非定常數值模擬的數值影響較大,因此需要在非定常數值模擬前對計算域內的流場分布進行預處理,將預處理后的穩定流場作為非定常數值模擬的初始流場。圖7(a)為經過預處理后的壓力分布云圖,這里水下流場的壓強分布符合以下壓力公式:

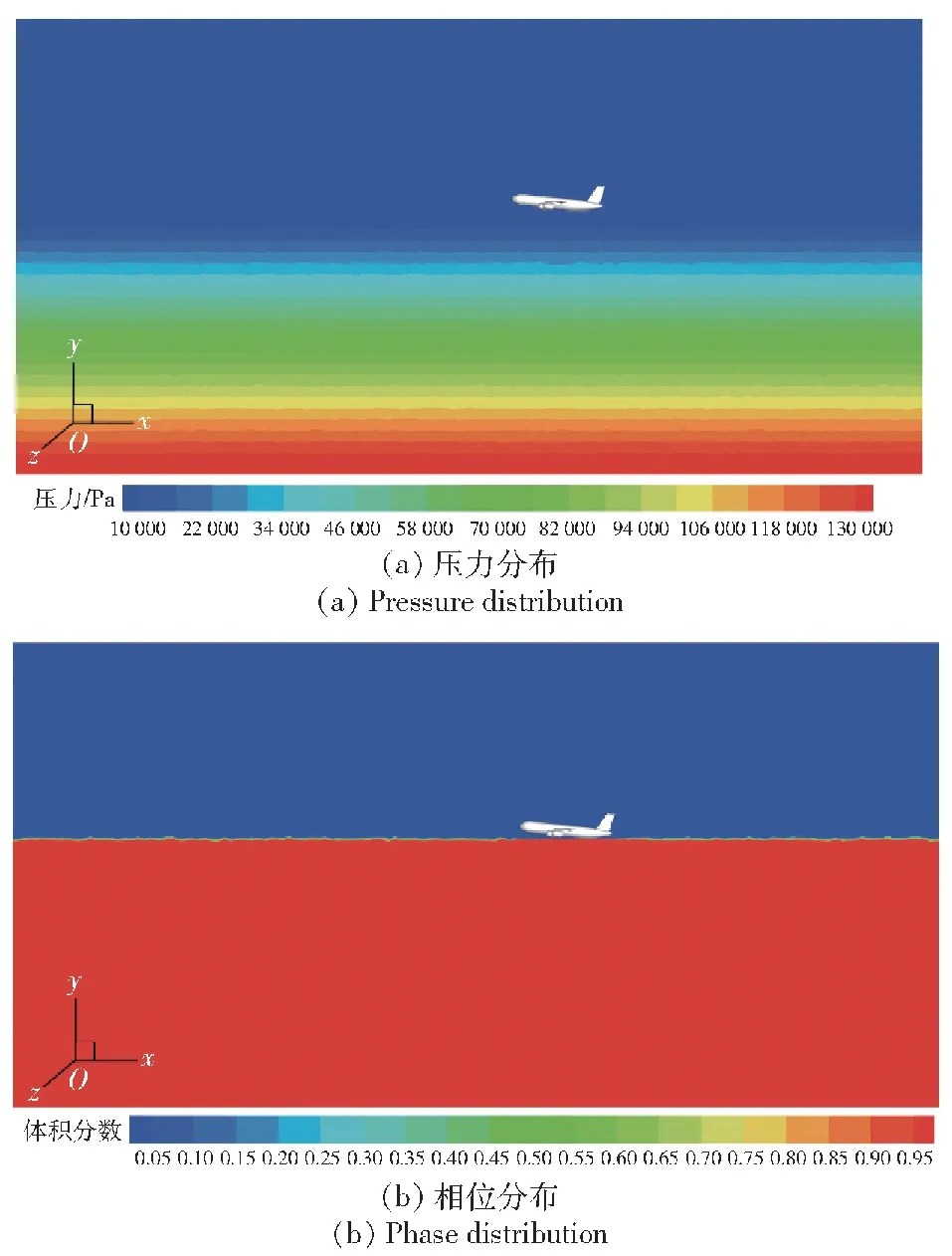
圖7 預處理后壓力云圖和相位云圖

pa=ρwgh

(9)

式中:pa為相對壓力;ρw為水的密度,ρw=998.2 kg/m3;h表示水的深度;操作壓強為標準大氣壓101 325 Pa。圖7(b)展示了水-空氣介質的相位分布云圖,空氣的體積分數為0,水的體積分數為1,水和空氣交界處的體積分數位于0和1之間。

2.2 網格收斂性驗證

對整體網格區域和移動網格區域的網格單元尺寸以及體網格加密程度進行設置與調整,繪制 4種不同網格數量的網格,4種不同網格的詳細信息如表1所示。分別采用4種網格對飛機以俯仰角度6°進行水上迫降數值計算,對比并分析其數值計算結果。

表1 4種不同網格的詳細信息

計算結果如圖8所示,圖8(a)、圖8(b)、圖8(c)和圖8(d)分別為采用4種不同網格計算得到的飛機水平速度、垂向速度、水平位移和垂向位移隨時間的變化曲線對比。經過比較曲線的變化趨勢可以看出:網格1和網格2的水平速度、垂向速度、水平位移以及垂向位移均與網格3和網格4的數值計算結果存在較大的差距,而網格3和網格4的數值結果的變化趨勢基本吻合,其數值誤差很小且在可接受范圍內。綜合考慮到計算精度、計算效率與計算資源,本文將采用網格3完成后面的數值計算與研究。

圖8 不同網格的數值結果對比

3 算例驗證

圖9展示了圓盤的幾何特征:一個厚度h=2.75 mm、半徑R=50 mm的圓盤模型有一個入水速度U和旋轉速度Ω,其中n為垂直于圓盤表面的單位矢量法線。圓盤的姿態由入水攻角α定義,ez為未受干擾的水面的單位法向量;圓盤的運動方向由沖擊角β定義,ex為與水面相切的單位矢量。圓盤與水的碰撞過程通過高速攝像機記錄。圓盤水漂實驗采用鋁制圓盤進行,圓盤與水的密度比為ρs/ρw≈2.7。

圖9 圓盤的幾何特征

為驗證數值方法的準確性,對文獻[8]水漂實驗中入水速度U=3.5 m/s、入水攻角α=35°和速度攻角β=20°實驗工況下的有旋轉(Ω=65 rot/s)和無旋轉(Ω=0 rot/s)圓盤水漂運動過程進行數值模擬。參照文獻[24],由于圓盤在水漂過程中高速自旋,姿態角α在整個碰撞過程中保持不變,在數值模擬過程中只放開ez方向與ex方向平移自由度。

圖10、圖11所示分別為圓盤在有旋和無旋狀況下的仿真結果與實驗拍攝結果[8]對比。由圖10和圖11可以看出,仿真結果獲得的不同時刻(時間間隔Δt=8.9 ms)液面噴濺形態和圓盤運動姿態均與實驗拍攝結果吻合較好。圖12展示了β=20°時不同α值的圓盤最小投擲速度vmin。從圖12中可以看出:本文算例采用VOF方法數值計算得到的結果相比于Yan等[24]采用SPH方法數值計算得到的結果更貼合Yan等的理論結果,且本文算例采用的基于VOF方法的數值計算結果與Yan等的理論結果誤差均小于4%,因此可以充分證明本文采用的數值方法符合數值計算精度要求。

圖10 圓盤水面滑跳實驗和數值計算的滑跳姿態對比(Ω=65 rot/s,上為實驗結果,下為數值模擬結果)

圖11 圓盤水面滑跳實驗和數值計算的滑跳姿態對比(Ω=0 rot/s,上為實驗結果,下為數值模擬結果)

圖12 β=20°時不同α值的圓盤最小投擲速度對比曲線

4 飛機水上迫降數值模擬

4.1 計算模型

如圖13所示,飛機的自身軸線與水面形成一個夾角α,定義該夾角α為飛機水上迫降時的入水俯仰角度。為研究不同俯仰角度α對水上迫降過程的影響,分別設置6°、8°、10°、12°、14°共5組俯仰角度。初始狀態時,飛機尾部與水面剛剛接觸,其水平初始速度為10 m/s,方向水平向左,豎直初始速度為0.5 m/s,方向垂直水平面向下。飛機不同俯仰角度的質量屬性如表2所示。

表2 飛機不同俯仰角度的質量屬性

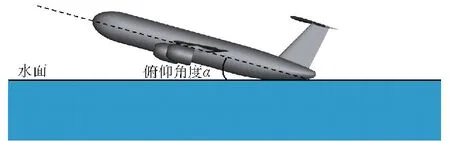
圖13 俯仰角度

4.2 計算結果與分析

采用第3節驗證過的CFD數值計算方法對飛機水上迫降過程進行仿真模擬,并對比不同俯仰角度情況下飛機在水上迫降過程中的數值變化與流場分布情況。圖14給出了俯仰角度為6°的飛機分別在t=0 s、t=0.1 s、t=0.2 s和t=0.3 s時的飛機姿態與水面變化情況。從圖14中可以看出,該數值方法能夠很好地捕捉飛機在水上迫降過程中的邊緣噴濺現象。

圖14 不同時刻的飛機姿態和水面變化(上為飛機姿態云圖,下為水面變化云圖)

圖15展示了不同俯仰角度的飛機在不同時刻的相位云圖。從圖15中可以看出飛機在不同時刻的姿態、位置、水面變化以及底部浸水情況:除了俯仰角度為6°的情況以外,其他俯仰角度在t=0.1 s時,發動機均未觸碰到水面;隨著時間的推進,俯仰角度為12°和14°的飛機在迫降過程中發動機底部均沒有完全浸入水中,而飛機尾部則全部浸入水中;從飛機尾部的浸水情況可以看出,飛機在整個迫降的過程中,垂向位移隨著俯仰角度的增大而增大,即飛機以較大俯仰角度入水的垂向位移更大。

圖15 不同時刻的相位云圖(上為飛機側面相位云圖,下為飛機底部浸水相位云圖)

圖16展示了飛機俯仰偏轉角度隨時間的變化曲線。從俯仰偏轉角度的變化趨勢可以看出,在迫降過程中,飛機先低頭后抬頭,其俯仰角度變化是由于飛機在迫降過程中受到的俯仰力矩造成的。經過對比分析可以看出,飛機的俯仰偏轉角度變化量隨著俯仰角度的增大而減小,即飛機以較大俯仰角度入水時的偏轉角度變化幅度越小,飛機不會大幅度抬頭,飛機的俯仰穩定性越好。

圖16 俯仰偏轉角度隨時間的變化

圖17分別給出了不同俯仰角度的飛機在不同時刻的壓力云圖。從圖17中可以看出不同時刻的飛機底部壓力分布情況:在t=0.1 s時,俯仰角度為6°的飛機發動機因最先觸碰到水面,底部會產生較大的壓力;俯仰角度為14°的飛機最先觸碰到水面的部位在機尾比較靠后的位置,飛機底部靠后的部位會產生較大的壓力,隨著迫降過程的進行,飛機底部的壓力逐漸減小且最大壓力區域向飛機前部移動;俯仰角度為14°的飛機發動機在t=0.2 s之前未接觸水面,發動機底部的壓力很小,最大壓力區域一直在機身尾部位置。由此可以推斷出:飛機底部的壓力分布與飛機底部的浸水情況有關,最大壓力區域均為飛機的浸水邊界,即飛機剛接觸水面的部分其壓力值最大。

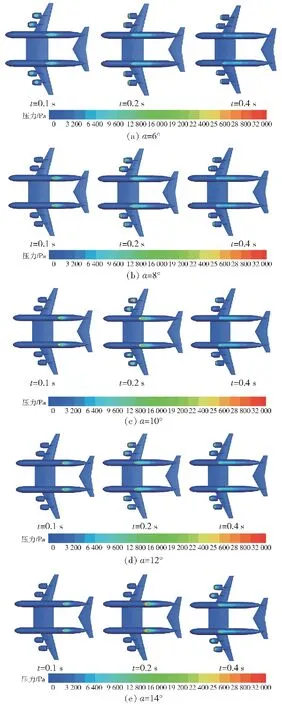
圖17 不同時刻的壓力云圖

圖18分別給出了飛機在不同俯仰角度情況下水上迫降的垂向速度和垂向位移隨時間的變化曲線。由圖18可以看出,飛機的垂向速度呈先增大后減小的趨勢,飛機的垂向位移呈先增大后緩慢減小的趨勢。分析飛機的垂向速度和垂向位移變化趨勢的原因,可以得出:在飛機水上迫降過程的初期,水對飛機的垂向作用力小于飛機自身重力,飛機的垂向速度不斷增大,垂向位移也隨之增大;隨著垂向位移的增大,水對飛機的垂向作用力逐漸增大,當飛機的垂向作用力等于飛機自身重力時,飛機的垂向速度達到峰值;隨著時間的推進,飛機的垂向作用力繼續增大并大于飛機自身重力時,飛機的垂向速度開始減小,飛機的垂向位移也逐漸減小并趨于平緩。

圖18 垂向速度和垂向位移隨時間變化

隨著俯仰角度的增大,飛機的垂向速度峰值越高,垂向速度達到峰值所需要的時間越長,飛機的垂向位移越大。當飛機以俯仰角度14°入水時,飛機的垂向速度從0.5 m/s最高增大到1.28 m/s,垂向速度增大了156%。而飛機以俯仰角度6°入水時,飛機的垂向速度從0.5 m/s最高增大到0.9 m/s,垂向速度增大了80%。因此可以得出:飛機以小俯仰角度完成迫降,垂向速度的變化幅度較小,相同時刻的垂向位移越小;相反,飛機以大俯仰角度完成迫降,垂向速度的變化幅度大,相同時刻的垂向位移越大。

圖19分別給出了飛機的水平速度和水平位移隨時間的變化曲線。由圖19可知:飛機的水平速度隨時間變化逐漸減小,其減小幅度先緩慢后快速再緩慢;俯仰角度越小,水平速度減小得越快,相同時刻的水平位移越小。由于飛機水上迫降過程最終需要完全停靠在水面上,即飛機的水平速度減小到 0 m/s,飛機以小俯仰角度完成迫降可以在較短的時間內完成水面停靠。

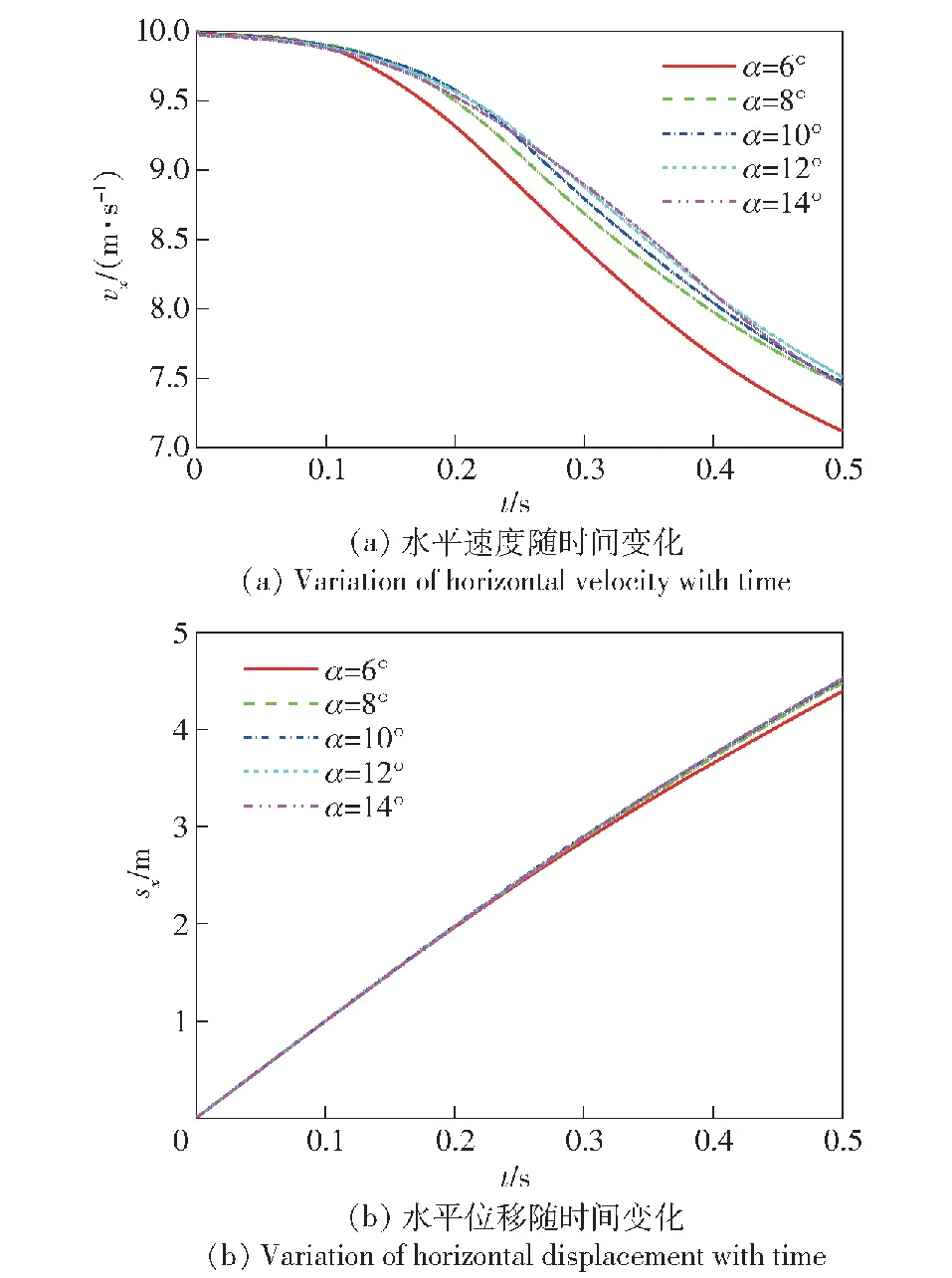
圖19 水平速度和水平位移隨時間變化

圖20分別給出了飛機在不同俯仰角度情況下受到的垂向作用力和垂向加速度隨時間的變化。由圖20可知:飛機在迫降過程中,水對飛機的垂向作用力的變化呈先增大后減小的趨勢,在水上迫降后期垂向作用力會在一個相對穩定的數值期間上下波動;飛機在入水砰擊過程中,隨著飛機垂向位移的增大,飛機的浸水面積逐漸增大,因此飛機的垂向作用力也逐漸增大;隨著飛機俯仰角度的增大,飛機受到的垂向作用力峰值越大,且到達峰值點的時間越長;飛機以14°俯仰角度入水,飛機受到水的垂向沖擊載荷最高達到了6 555.025 N,是飛機自身質量的1.83倍;飛機以6°俯仰角度入水,飛機受到水的垂向沖擊載荷最高達到了4 988.928 N,是飛機自身質量的1.39倍。因此,飛機以大俯仰角度進行水上迫降對飛機的結構強度要求更高;垂向加速度變化的趨勢是先減小后反向增大再減小,在水上迫降后期垂向加速度也會在一個相對穩定的數值期間上下波動;飛機的俯仰角度越大,垂向加速度的變化幅度越大。

圖20 垂向作用力和垂向加速度隨時間變化

圖21分別給出了飛機在不同俯仰角度情況下水平作用力和水平加速度隨時間的變化曲線。由圖21可知:飛機在迫降過程中受到的水平作用力呈先增大后減小的趨勢,因此飛機的加速度也呈先增大后減小的趨勢;隨著飛機俯仰角度的增大,飛機受到的水平作用力峰值減小,水平加速度峰值也越小;飛機以6°俯仰角度入水時,飛機受到水的水平作用力較大,其加速度峰值和波動幅度都比較大,因此飛機的水平速度減小得更快,從而證實了飛機以小俯仰角度完成迫降可以在較短的時間內完成停靠的結論。

圖21 水平作用力和水平加速度隨時間變化

5 結論

1)在飛機水上迫降過程中,飛機因受到的俯仰力矩的作用會先低頭后抬頭,飛機的俯仰偏轉角度變化量隨著飛機俯仰角度的增大而減小,即飛機以較大俯仰角度入水時的俯仰偏轉角度越小,俯仰穩定性越好。

2)在飛機水上迫降過程中,飛機底部的壓力逐漸減小且最大壓力區域向飛機頭部移動。飛機底部的壓力分布與飛機底部的浸水情況有關,最大壓力區域為飛機的浸水邊界,即飛機剛接觸水面的部分壓力值最大。

3)在飛機水上迫降過程中,俯仰角度越大,飛機的垂向速度峰值越大,飛機的垂向位移越大。即俯仰角度越大,飛機的浸水位移越大,飛機在水上迫降過程需要更深的浸水位移才能使飛機完全停下來。

4)在飛機水上迫降過程中,俯仰角度越小,飛機的水平速度減小得越快,飛機的水平位移越小。即飛機以小的俯仰角度完成迫降可以在較短的時間內完成水面停靠。

5)在飛機水上迫降過程中,俯仰角度越大,垂向作用力和垂向加速度的變化幅度越大,飛機受到的垂直作用力和垂直加速度的峰值越大;飛機以較小的俯仰角度完成水上迫降時,飛機受到的水的垂向作用力影響較小,垂向加速度變化幅度較小。

6)在飛機水上迫降過程中,俯仰角度越小,水平作用力和水平加速度的變化幅度越大,水平作用力峰值越大且達到峰值所需要的時間越長;飛機以較大的俯仰角度完成水上迫降時,飛機受到的水的水平作用力影響較小,水平加速度變化幅度較小。

7)該型雙機身飛機在水上迫降過程中,俯仰角度越大,飛機受到的水的垂向作用力影響較大;俯仰角度越小,飛機受到的水的水平作用力和俯仰力矩影響較大。考慮飛機在迫降過程中需以較快的時間停靠下來,俯仰角度取6°比較合理;綜合考慮飛機在迫降過程中水平方向、垂直方向以及俯仰方向的穩定性,俯仰角度取10°～12°比較合理。

綜上所述,本文可為飛機水上迫降和跨介質飛行器入水砰擊等問題提供參考價值。