水下航行器能源動力系統建模仿真與實驗研究
張劍, 沈琳
(1.中國科學院 電工研究所 電力電子與電氣驅動重點實驗室, 北京 100190;2.中國科學院大學 電子電氣與通訊工程學院, 北京 100049;3.齊魯中科電工先進電磁驅動技術研究院, 山東 濟南 250102)
0 引言
以直流區域配電為特征的第二代能源動力系統(EEPS),具有良好的機動性、靜音性、布置靈活性以及較低的燃油消耗率[1],已成為未來艦船動力系統的發展方向[2]。艦船的EEPS以電能作為能量形態,在綜合運用電力變換、傳輸等技術的基礎上,通過對傳統艦船中相對獨立的動力和電力兩大系統的整合,在滿足推進系統高速機動性對電能需求的同時[3],為武器等其他負載提供電力能源,實現了對推進系統、武器系統、輔助設備所需電能的動態分配和優化管理[4],簡化了艦船動力系統的結構,實現了更高的功率密度和配置的靈活性,帶來了艦船綜合性能的大幅提升,EEPS已成為現代電力推進艦船重要的組成部分[5]。
艦船的EEPS構成復雜,其典型的系統配置包括柴油機及其控制器、發電機及控制器、電動機及控制器和螺旋槳推進裝置,各個組件間存在復雜的電磁耦合和機電耦合關系,目前還無法得到系統啟動加載、負荷切換等動態過程的解析解,因此也無法基于解析法來研究EEPS的上述復雜動態過程。同時,艦船電力系統與陸用大電網相比,系統容量小且孤立,艦船電力系統與陸用大電網存在明顯的差異。建立被控對象的數學模型是對航行器EEPS進行特性分析和控制系統設計的基礎,通過建立系統的計算機模型并進行仿真,可以完成對系統的穩態、動態過程分析及控制策略優化,從而縮短臺架試驗及實航驗證時間,降低系統的研發周期和成本[6]。
隨著以全電力推進為特征的“全電艦船”不斷涌現,艦船電力系統建模方面的相關研究逐漸增多,應用的理論與建模方法也越來越多樣化。國內外學者針對柴油機建模和仿真進行了大量研究,根據建模原理、復雜程度、應用范圍的不同,大致可以分為線性模型[7-9]、非線性模型[10]及系統辨識模型[11]三類,針對不同應用場合有不同復雜度的模型可供選擇,在保證建立的柴油機模型與柴油機實物輸入輸出特性一致性的前提下,如何降低模型復雜度,提高計算速度,達到實時仿真的要求,以及如何設計合理的參數抽取方法都是尚未解決的問題;三相同步電機在中小型船舶中具有廣泛的應用前景,國內外針對船用電勵磁三相同步電機展開了較多的理論和應用研究,新興的功率密度更高的永磁同步電機(PMSM)的主磁場由永磁體產生,這與電勵磁同步電機在工作機理上存在根本性不同。多年來,PMSM的運行理論基本建立在對時間向量和空間矢量分析的基波分析理論上,在時域中采用連續模型[12-13]對PMSM進行描述是一種較通用的方法,考慮到以數字信號處理器(DSP)為控制核心的變流器系統基于數字化技術,其控制過程是離散化的,為更好地進行變流控制策略與電機本體的匹配設計,建立PMSM的精確的離散化模型具有迫切的需求;在研究螺旋槳動態特性時,將螺旋槳和船體作為一個整體進行建模是一種通用方案[14],“船-槳”建模方法相對比較成熟,建立的模型可以真實地反映螺旋槳的動態過程,雖然模型中相關參數可以通過工程經驗進行獲取,但是如何評估所獲得參數的準確性以及模型與實物系統的對比驗證等問題,并未得到完全的解決。
基于上述分析可知,國內外學者針對EEPS各關鍵組件的建模方法很多,但是如何平衡各組件模型復雜度和精確度的關系,在此基礎上獲得滿足實時仿真需求的實用模型的方法并不完善。同時,基于各組件模型構建的系統仿真模型與EEPS實物系統的對比驗證工作進行得并不充分。
本文以某中型水下航行器EEPS為研究對象,在對其關鍵組件進行運行機理分析和數學建模的基礎上,搭建包括柴油機、PMSM、變流器和螺旋槳等組件的EEPS一體化仿真平臺,開展EEPS系統級仿真工作,并與搭載真實EEPS系統的航行器地面實驗及實航海試的實驗結果進行詳細的對比與分析,驗證所構建的仿真平臺與EEPS實物系統動靜態性能的一致性。
1 航行器EEPS特性分析及數學建模
圖1所示為一種基于直流區域配電架構的水下航行器EEPS的結構示意圖。EEPS主要由前級發電子系統和后級電推進子系統組成,采用的是較為典型的“交-直-交”級聯型拓撲、直流區域配電架構。柴油機作為原動機通過連軸裝置與PMSM進行機械連接,產生的電能經整流器整流后接入匯流排,供后級電推進子系統及其他船載用電設備使用,電推進子系統推動螺旋槳旋轉,為航行器行進提供驅動力。

圖1 一種典型的水下航行器EEPS架構示意圖
1.1 柴油機及其轉速控制系統建模分析
為構建柴油機的實用化動態仿真模型,在對柴油機內部燃燒、熱力等瞬態過程的抽象及簡化基礎上,根據柴油機各組成部分的工作原理確定模型的數學結構形式,通過測試分析方法完成模型中關鍵參數的抽取,在保證所建模型與柴油機實物輸入輸出特性一致性的前提下,提高仿真的速度,滿足EEPS復雜系統實時仿真的要求。
1.1.1 柴油機及其轉速控制系統建模
柴油機及其控制系統如圖2所示,包括調速器、油門執行器及柴油機機體三部分。調速器實現柴油機曲軸輸出轉速的閉環控制;油門執行器根據調速器輸出的控制信號調節油門齒桿位置,通過對柴油機本體供油量的調節,實現轉速控制。圖2中,ω*為曲軸角速度指令值,Δω為曲軸角速度控制誤差,η*為齒桿位移指令,η為齒桿位移,ω為曲軸角速度。

圖2 柴油機及其轉速控制系統框圖
忽略柴油機的摩擦力矩,根據達朗倍爾原理,柴油機的機械運動方程可以表示為
(1)
式中:Je為柴油機及軸系轉動慣量;z為油門齒桿位移量;Td、Tr、TL分別為輸出轉矩、阻力矩及負載轉矩。
忽略負載轉矩的擾動,并假設擾動作用下曲軸角速度、輸出轉矩及阻力矩產生的小信號變化量分別為Δω、ΔTd、ΔTr,對式(1)進行小信號分析,可得
(2)
與轉矩有關的小信號變化量可以表示為
(3)
由式(2)及式(3)可得
(4)
設ωn為柴油機曲軸額定角速度,ze為柴油機油門齒桿額定位移量,將式(4)中的小信號變化量基于各自信號的額定值進行標幺化處理,得到
(5)
式中:φ=Δω/ωn;η=Δz/ze。
將式(5)變化到頻域,考慮到燃油從噴入氣缸到完成燃燒并輸出轉矩存在一個延時時間τ,得到包括延時環節e-τs(s為拉普拉斯算子)的柴油機本體傳遞函數為
(6)

柴油機的油門執行器以直流伺服電機為驅動單元,并通過齒輪傳動機構帶動齒桿運動,油門執行器的輸出為齒桿位移η,其控制框圖如圖3所示。圖3中,uD為齒桿位移控制誤差,Ce為直流伺服電機的電壓常數,TD為直流伺服電機1階慣量時間常數,GD為直流伺服電機傳遞函數,ωD為直流伺服電機轉速,kD為傳動機構機械時間常數,Gη為傳動機構傳遞函數。
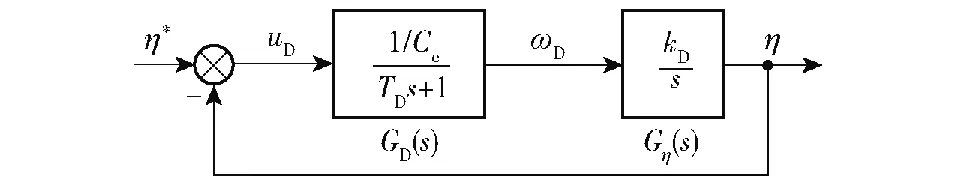
圖3 柴油機油門執行器控制框圖
直流伺服電機傳遞函數:
(7)
傳動機構傳遞函數:
(8)
TD=JRD/(CmCe),Cm=Tsn/isn,Ce=E/nsn
(9)
式中:J、RD分別為轉動慣量和電樞電阻;nsn、Tsn、isn、E分別為伺服電機的轉速、轉矩、勵磁電流及空載電動勢的額定值。
由式(7)、式(8)得到油門執行器的閉環傳遞函數為
(10)

本文研究的柴油發電機組參數如表1所示,使用德國HEINZMANN電子調速器,調速器采用PID控制,將式(6)中涉及到的系數Kη歸入PID參數中,得到柴油機及其控制系統的結構框圖如圖4所示。

表1 柴油發電機組參數

圖4 柴油機及其控制系統結構框圖
1.1.2 柴油機模型參數抽取
圖4所示柴油機模型中待確定的參數為Tα、τ、Wn、ξ。為獲取這些參數,需要計算柴油機的自穩定系數F[15]為
(11)
式中:Tdn為柴油機額定轉矩。
基于自穩定系數F可計算柴油機加速時間常數為
Tα=Je/F=Jeωn/Tdn
(12)
式(6)中,τ為燃油燃燒過程引入的純滯后時間[16],該值的計算公式為,
τ=(60×Nst)/(Ncyl×ne)
(13)
式中:Nst、Ncyl、ne分別為柴油機沖程數、氣缸數及額定轉速。
式(10)表達的油門執行器是一個典型的2階系統,利用經典控制理論中給出的2階系統動態跟隨性能指標和Wn、ξ的關系,可以得到[17]
ξWn=1/(2TD),ξ=0.707
(14)
聯立式(9)、式(14),可求得固有角頻率為
Wn=4.242
(15)
利用式(12)~式(15)可以進行柴油機模型參數的計算。除轉動慣量Je外,其他參數都可以通過前述方程及表1求得。本文給出了一種針對柴油機及其輸出軸系的轉動慣量測定方法,基本思想是控制與柴油機同軸連接的發電機,使其運行在電動模式并輸出恒定轉矩,發電機反拖柴油機到特定轉速,記錄加速過程中轉矩施加時間及柴油機轉速的變化率,根據剛體定軸轉動定律可以計算轉動慣量如下:
Je=MT/?
(16)
式中:MT為反拖柴油機運行的外加轉矩(N·m);?為柴油機輸出軸角加速度(rad/s2)。
發電機與柴油機同軸連接并運行于電動模式,外部力矩作用下的柴油機轉速響應曲線如圖5所示。

圖5 外部力矩作用下的柴油發電機組轉速響應曲線
由圖5可以得到:
式中:KN為轉矩電流比,由電機的特性決定,在電機的恒轉矩區KN為常數,可以通過實驗測得,本文永磁電機的KN=3;Is為電機相電流幅值。則有
Je=MT/?=MTΔt/Δω=12.84 kg·m2
(17)
將式(17)代入式(12),得到
Tα=Jeωn/Tdn=1.683 s
(18)
最后得到表1所示參數的包含柴油機機體及油門執行器的柴油機本體系統數學模型如下:
(19)
1.1.3 柴油機調速控制器設計
圖6所示柴油機本體系統的傳遞函數為4階,可以對高階系統進行降階處理,等效為2階系統后,再按照經典控制理論的最優整定方法[18]完成柴油機調速控制器Gc(s)的設計。

圖6 柴油機及其調速控制器結構框圖
Gc(s)分別采用PI或PID的結構形式,進行柴油機系統在突加及突卸額定轉矩負載時轉速響應的對比仿真,結果如圖7所示。

圖7 采用不同類型的調速控制器時的轉速響應
對比圖7中的兩條轉速響應曲線可以看出,在柴油機的調速控制器Gc(s)中增加微分項,利用微分項對轉速誤差的預測作用可以有效地抑制轉速的超調,因此柴油機的調速控制器一般采用PID結構。
1.1.4 柴油機模型驗證
為驗證本文搭建的柴油機模型的正確性,對柴油機空載啟動及突加、突卸負載工況進行仿真,并與柴油機的實際實驗曲線進行對比。
圖8所示為柴油機空載啟動過程中轉速的仿真及實驗曲線,從中可以看出柴油機從零速啟動到怠速以及從怠速升速到額定轉速兩個過程中,仿真波形與實際實驗波形具有很好的吻合度。

圖8 柴油機空載啟動過程轉速響應的仿真與實驗結果對比
圖9所示為柴油機工作在額定轉速,突卸100%額定負載時的轉速響應仿真與實驗曲線的對比結果,可以看出動態過程中本文建立的柴油機模型與柴油機實物系統的轉速響應具有較好的一致性。

圖9 突卸負載過程柴油機轉速響應的仿真與實驗結果對比
1.2 三相交流PMSM及變流控制系統建模
PMSM的運行理論基本上建立在對時間向量和空間矢量分析的基波分析理論上,而永磁電機的基波模型分為時域中的連續模型[19]和z域中的離散模型[20]兩大類。考慮到基于DSP的變流器系統基于數字化技術加以實現,實現過程是離散化的,建立被控對象永磁電機的離散化模型有利于變流控制策略與電機本體的匹配設計,因此研究電機的離散化建模方法十分必要。以文獻[20]為代表的一類常用的離散建模方法基于前向歐拉法實現對永磁電機微分方程的求解,求解過程設置了較強的假設條件,所得到的離散化解精度并不高。作為一種改進,本節提出一種針對PMSM的離散域建模方法,具有更高的精度。
1.2.1d、q軸坐標系下PMSM離散化模型
在d、q軸坐標系下,矢量矩陣形式的PMSM狀態空間表達式為
didq/dt=Aidq+Budq+C
(20)
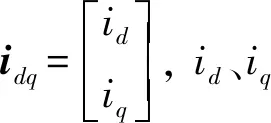
為獲得PMSM離散域中的數學表達式,首先需要求取式(20)所示狀態方程在時域中的全解,然后進行離散化。假設變流控制系統的控制周期為Ts,則處于第k拍和第k+1拍之間的時刻t可以表示為t∈[kTs,(k+1)Ts],采用0階保持器實現離散系統向連續系統的轉換,對式(20)所示系統的時域解進行離散化,得到PMSM在離散域的數學模型,如式(21)所示,詳細推導過程見附錄A。
(21)

根據第kTs時刻的idq(k)、udq(k),基于式(21)可以精確計算得到(k+1)Ts時刻的idq(k+1)及電磁轉矩Te(k+1)。
附錄A所給出的電機模型同時適用于凸極式及表貼式PMSM,由于其離散化過程未涉及近似求解,與傳統方法相比,本文所求得的PMSM離散域模型具有更高的精確度。
1.2.2 PMSM控制策略
圖1所示系統中,永磁同步發電機-整流器組成的AC-DC系統以及由逆變器-永磁同步推進電機組成的DC-AC系統,由于逆變器和整流器的硬件均基于三相全橋拓撲構建,且都以PMSM為被控對象,控制策略上是類似的。
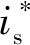
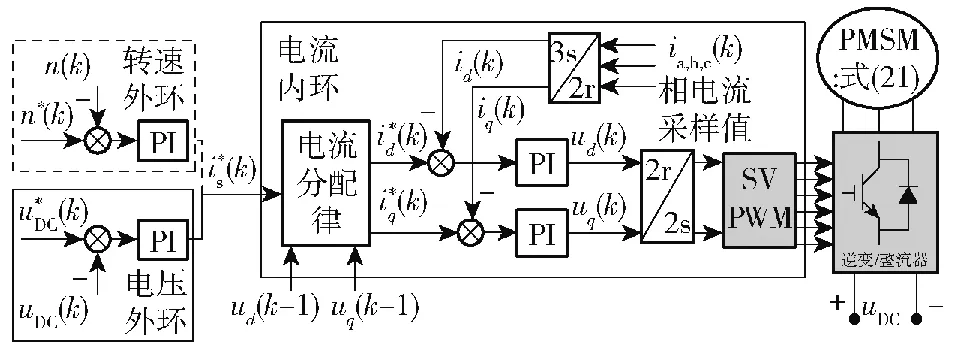
圖10 d、q軸坐標系下PMSM統一控制框圖
1.3 航行器-螺旋槳系統建模分析
螺旋槳是航行器電力推進子系統的最終執行機構,建立其數學模型是分析航行器在各種工況下的負載特性的基礎。定義螺旋槳的進速比為槳葉旋轉一周后,螺旋槳軸向前行進的距離與槳直徑之比。在航行器航行時,其航速或者螺旋槳轉速的變化都會引起進速比的變化,進速比的變化又將進一步引起螺旋槳負載轉矩的變化。為更好地體現螺旋槳的動態特性,本文采用將螺旋槳和航行器作為整體進行建模的方法。
1.3.1 航行器-螺旋槳系統模型
進速比J′的定義為
(22)
式中:vp為螺旋槳前進速度;Np為螺旋槳的轉速;D為螺旋槳直徑。
螺旋槳的轉矩系數K′M和推力系數K′P定義為
(23)
式中:M為螺旋槳負載轉矩;ρ為水的密度;p為螺旋槳推力。
航行器航速vs與螺旋槳前進速度vp滿足
vp=(1-w)vs
(24)
式中:w為伴流系數。
由式(23)可知,螺旋槳推力p以及作用到航行器上的有效推力pe之間滿足
(25)
式中:t為推力額減系數。
由式(23)可得螺旋槳負載轉矩M滿足
(26)
航行器所受阻力Rf滿足
(27)
式中:A0為航行器表面的濕面積;ζ為總阻力系數。
綜上,航行器的機械方程可以表示為
(Ms+ΔM)·dvs/dt=pe-Rf
(28)
式中:Ms為航行器的質量;ΔM為隨航行器運動的附著水的質量,一般取ΔM=(5%~15%)Ms。
1.3.2 航行器及其螺旋槳推進系統一體化建模
螺旋槳與推進電機同軸相連,推進電機輸出轉矩驅動螺旋槳旋轉為航行器的航行提供動力。基于式(21)~式(28),建立包含推進電機/螺旋槳推進系統的航行器一體化模型,如圖11所示。

圖11 航行器及其螺旋槳推進系統一體化模型
根據設定的航速,可以由式(22)和式(24)計算得到螺旋槳的轉速Np,螺旋槳與推進電機同軸連接,因此螺旋槳與PMSM的轉速相同,該值將作為推進電機的轉速指令值,按照圖10給出的電機控制策略,控制推進電機按照指令轉速進行旋轉,輸出轉矩,抵消螺旋槳旋轉過程中的阻力矩,實現對航行器的推進。
1.3.3 航行器及其推進系統一體化模型的參數獲取
圖11所示模型較全面地反映了推進電機-螺旋槳-航行器三者之間的相互作用,但模型較復雜,且模型中螺旋槳推力系數K′P、轉矩系數K′M等關鍵參數在實踐中很難直接獲得,一般都是通過經驗公式來間接求取,參數準確性將直接影響模型的精度。
由式(23)可知,螺旋槳的推力系數K′P,轉矩系數K′M和進速比有關,航行器在特定航行條件下(裝載、氣候、海面狀況等條件不變)航行時,可認為進速比為常數,由式(22)和式(26)可以將螺旋槳轉矩M的方程簡化為
(29)
式中:等效轉矩系數KM為常數。螺旋槳轉矩M即為驅動電機的負載轉矩。
航行器的前向、定常航行狀態對應以下4種典型工況,典型工況下的航行特性可以歸納為:
1) 系泊航行特性:表征航行器滿載且航速為0 kn時槳速與槳轉矩之間的關系,正向起車時航行器航速接近為0 kn,可以等效為系泊特性;
2) 自由航行特性:表征航行器滿載航行在靜水中槳速與槳轉矩之間的關系;
3) 拖曳航行特性:航行器在大風浪中逆風航行或拖動拖曳性負載(如拖船),推進阻力增大,螺旋槳轉矩特性上移,介于自由航行與系泊航行特性之間;
4) 輕載順航特性:船舶阻力較小,螺旋槳特性處于自由航行特性之下。
航行器運行在上述4種典型工況下,螺旋槳轉矩特性均滿足式(29),差別僅在于等效轉矩系數KM取值不同。通過實航獲取上述航行器的“轉矩-槳速”數據,利用曲線擬合可以精確地獲得螺旋槳的轉矩特性曲線。
以本文研究的航行器本體及配套的螺旋槳為對象,通過實航測試的方式,分別測得上述4種典型工況下螺旋槳的轉矩特性曲線,如圖12所示。

圖12 典型航行狀態下螺旋槳轉矩特性
由圖12可以看出,4種航行狀態的進速比滿足0=J′1 系泊航行特性: (30) 自由航行特性: (31) 系泊航行特性和自由航行特性是航行器螺旋槳特性的兩種最常用的形式。基于式(30)、式(31)所分別表示的航行器在系泊航行和自由航行兩種典型工況下的螺旋槳轉矩特性,可以較精確地反映推進電機與螺旋槳間的相互作用情況。 為了對某中型航行器EEPS的動態及穩態特性進行仿真研究,基于本文建立的數學模型,在MATLAB軟件的Simulink仿真環境建立包括柴油機、PMSM、變流器(整流器/逆變器)和螺旋槳在內的航行器EEPS仿真模型,并搭建系統的一體化數字仿真平臺,如圖13所示。 圖13 航行器EEPS一體化數字仿真平臺 基于上述仿真平臺,對柴油機空載啟動、直流母線電壓建立以及螺旋槳由零速啟動并升速到額定轉速的完整過程進行仿真。為減少仿真程序的運行時間,在仿真中人為地壓縮了啟動過程,這一點與航行器的實航實驗略有不同,其他方面則模擬實航工況。仿真過程如下:0 s末啟動柴油機,發電機組隨著柴油機轉速升高,輸出直流電壓達到額定值(750 V),6 s末螺旋槳由零速啟動并升速到最高轉速(2 000 r/min),螺旋槳升速過程中推進電機的負載轉矩按照航行器的系泊特性曲線進行設定。為評估推進系統啟動方式對EEPS的影響,分別進行螺旋槳轉速指令斜坡給定及階躍突加給定兩種方式的仿真。圖14為螺旋槳轉速指令采用斜坡給定時的仿真結果,指令值每秒增加200 r/min,可以看出整個啟動過程中能源動力系統的直流側電壓及原動機轉速均保持設定值,螺旋槳升速過程平穩;螺旋槳的轉速指令設定采用分段、階躍給定的方式,得到仿真結果如圖15所示。由圖15可以看出,轉速指令突增后一段時間內螺旋槳及推進電機承受很大的過載轉矩,且升速瞬間母線電壓及電流均有較大幅度的波動,表明這種啟動方式對航行器的電網造成很大的沖擊,嚴重時會危及電網的穩定性。因此在實際的運行中,航行器由零航速啟動時推薦采用分段啟動,且啟動過程中螺旋槳轉速指令采用斜坡給定的方式,以有效緩解對航行器傳動軸系及直流電網的沖擊。 圖14 槳速指令斜坡給定時的航行器啟動、加載過程 圖15 槳速指令階躍給定時的航行器啟動、加載過程 航行器及EEPS的實物如圖16所示,系統組成原理參見圖1。為驗證仿真模型與實物系統的一致性,開展典型工況下仿真與實驗的對比研究。在1.1節圖8、圖9中已經驗證了本文搭建的柴油機模型與柴油機實物的一致性,下面針對圖16所示航行器EEPS的前級發電子系統和后級電推進子系統分別進行仿真,并將仿真結果與實驗結果進行對比,以驗證模型的準確性。 圖16 航行器及EEPS實物系統 結合航行器的真實工況,共設計以下3組對比實驗。 突加負載實驗用于模擬螺旋槳突然加速、發電子系統載荷突增工況下的直流側電壓變化情況,本實驗在地面進行,以突加電阻性負載的形式模擬發電子系統的負載突增。兩次分別突加75 kW電阻性負載,仿真結果及實驗結果如圖17所示,突加負載后在直流側電壓跌落量及電壓恢復時間兩個主要指標上,系統性能良好,且仿真結果及實驗結果均有很高的一致性。 圖17 突加負載時發電機組輸出直流電壓仿真與實驗結果對比 發電子系統甩負荷測試用于模擬實航惡劣海況下由于螺旋槳浮出水面或電推進子系統突發故障引起的直流側負載突卸,在臺架實驗中通過對推進電機的逆變器突封PWM脈沖來模擬。發電機組轉速及輸出直流電壓的仿真及實驗結果如圖18所示,從中可以看出,由負載突卸到系統達到再次穩態過程中,在直流側電壓、發電機轉速波動及響應時間等關鍵技術指標方面,仿真與實驗結果具有較好的一致性。 圖18 甩負荷測試過程中發電機組轉速、輸出直流電壓仿真與實驗結果對比 分別通過實航實驗及仿真獲取螺旋槳轉速由 1 200 r/min 逐級增加到2 000 r/min過程中永磁同步推進電機的電流、螺旋槳轉速曲線,如圖19所示。為減小對系統的沖擊,在進行實航海上實驗過程中,螺旋槳轉速指令按照斜坡給定的方式進行設置,實航相關數據通過CAN總線采集并由數據記錄儀記錄,數據記錄間隔為0.5 s,截取的記錄總時長約為18 min。由于仿真持續時間受到計算機性能的限制,在仿真中螺旋槳轉速指令采用階躍給定的方式,將整個仿真工況的總時長控制在16 s。由于永磁同步推進電機采用MTPA的電流分配策略,在穩態下電機相電流與輸出轉矩具有一一對應關系,通過航行實驗電機電流數據可以推算出電機輸出轉矩情況。 圖19 電推進子系統轉速、轉矩特性仿真與實航測試結果對比 圖19表明:穩態工況下,同樣螺旋槳轉速下,仿真與實航實驗時推進電機的穩態電流幅值相同(由于分別采用了階躍給定和斜坡給定的方式,動態過程電流幅值不同),電流幅值相同則表明輸出轉矩相同,證明了本文建立的電推進子系統模型與實際系統的轉速-轉矩特性具有較好的一致性;實航實驗動態及穩態過程中電機電流實際值快速跟蹤指令值的變化,表明電流閉環控制系統性能良好。 本文以某中型水下航行器EEPS為研究對象,在對EEPS各關鍵組件進行特性分析和機理建模的基礎上,搭建了包括柴油機、PMSM、變流器和螺旋槳等核心組件的EEPS一體化仿真平臺。為驗證仿真平臺的準確性,進行了系統級的全工況仿真并與EEPS實際系統搭載航行器所進行的實航測試數據進行了對比。得出以下主要結論: 1) 本文建模方法較好地平衡了模型精度和復雜度的關系,解決了模型參數獲取困難的痛點問題,所構建的EEPS系統級仿真平臺與實物系統的動靜態性能之間具有較高的一致性,仿真模型及仿真平臺可用于實時仿真,具有實用性。 2) 基于上述仿真平臺,采用不同的啟動策略,對航行器零速啟動及加載過程進行了對比仿真,歸納出了螺旋槳轉速指令值的設定宜采用斜坡給定、分段提速的策略,該提速策略可以有效地減小航速變化過程中負載突變對航行器傳動軸系及直流電網的沖擊,本文策略已在航行器的海試中得到了驗證及應用,實際效果好。 3) 通過本文建立系統的仿真模型并進行仿真,可以完成對系統啟動加載、負荷切換以及多套發電機組并入切出等復雜的動態過程分析及控制策略優化,從而縮短臺架實驗及實航驗證時間,有效降低系統的研發周期和成本。 4) 本文提出的建模思路及建立的實時仿真平臺為船用EEPS控制策略的設計提供了工作的基礎,也可以為其他具有類似結構的級聯型機電能量變換系統的研究提供有益的借鑒。2 系統仿真及分析


3 仿真與實驗對比

3.1 發電子系統突加負載測試

3.2 發電子系統甩負荷測試

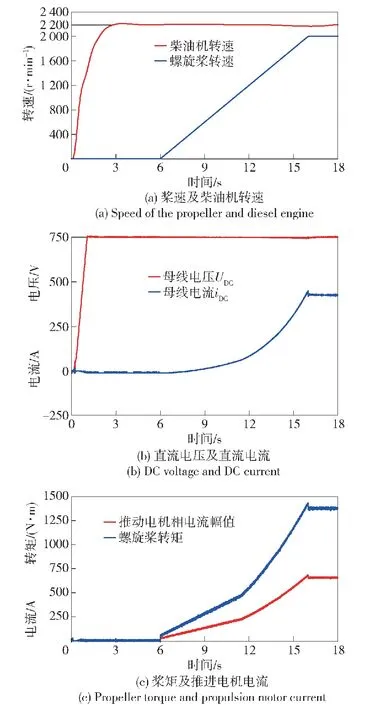
3.3 電推進子系統“轉速-轉矩”特性

4 結論

