基于工件振動和刀具結構的周銑表面形貌分析與預測

劉揚, 秦國華, 吳竹溪, 婁維達, 賴曉春

(1.南昌航空大學 航空制造工程學院, 江西 南昌 330063; 2.江西省教育廳 江西省教育國際合作與教師發展中心, 江西 南昌 330083)

0 引言

動態的切削過程勢必造成工件產生振動,影響工件的加工表面形貌,進而影響零件的物理、機械性能以及實用壽命。

趙軍等[1]基于自由曲面方程運算出刀具刃線運動包絡面,對球頭銑刀加工的表面形貌進行了建模和仿真,結果表明:在工件加工面為平面時刀軸擺角的選擇對表面形貌有較大影響;加工面為自由曲面時,刀軸擺角的選擇對表面形貌影響不大。Liu等[2]開發了一種銑削加工表面的仿真系統,使刀具-工件相互作用隨刀具運動的動態跟蹤成為可能,通過對刀具中心運動和刃口形狀的修改,將刀具跳動和磨損的影響分別納入開發的模型中,從而更準確地描述被加工表面的微觀特征。Lavernhe等[3]利用N-buffer方法建立了表面形貌的預測模型,經預測模型分析表明,刀具傾角對三維形貌的影響較大。Fernando等[4]在量綱分析與有限元分析的基礎上,對AISI H13鋼球頭銑削表面形貌進行數值模擬,并用銑削實驗驗證了該模型的有效性。Schmitz等[5]研究了端銑加工過程由刀具的位置偏移以及刀具傾斜所導致的刀具安裝誤差對加工工件表面形貌的影響,通過仿真驗證了跳動量、表面粗糙度、穩定性和表面定位誤差之間的關系。Chen等[6]建立了基于微細銑刀幾何特征的曲面生成模型,研究了軸向跳動和徑向跳動對表面形貌的影響。Zhang等[7]采用接收耦合法得到動態特性函數,并結合銑削力模型計算刀具的動態撓度,提出了一種新的表面形貌模型,通過將刀具偏轉引入微側銑刃軌跡方程,分析認為影響微側向銑削表面形貌的最重要因素是主軸轉速、進給速度、徑向切削深度和銑削方法。Arizmendi等[8]提出了一種預測面銑表面三維形貌的新方法,結果表明端面銑刀刀片之間的軸向跳動顯著影響表面形貌。Wang等[9]考慮了刀具平行軸偏移和位置角的影響,改變了橢圓中心和切削刃交點的位置,通過建立表面形貌預測模型分析了影響粗糙度發展趨勢的因素。上述研究工作主要是在刀具切削刃幾何形狀的基礎上,進一步考慮了刀具的跳動、偏轉等對加工表面形貌的影響。

Zeroudi等[10]建立了自由銑削時刀具的切削力預測模型,通過考慮切削力對加工工件表面形貌的影響,建立了銑削工件表面形貌的重組模型。Chen等[11]提出了一種預測薄壁零件彈性變形后表面形貌的數值模型,針對切削過程中的幾何特征建立了薄壁零件的切削力模型,研究了刀具-工件之間的嚙合關系。Peng等[12]建立了一種考慮刀具傾斜、顫振、跳動、切削力和材料的塑性變形模型,并證明了模型推薦的參數可以很好地控制三維表面形貌。宋文剛等[13]采用表面算術平均高度和表面最大高度對表面形貌進行了表征,建立了考慮工件初始表面幾何狀態的切削層模型,利用兩工步銑削試驗對切削層模型進行了驗證,結果表明工件初始表面幾何狀態與第二工步銑削的銑削力和表面粗糙度參數呈正相關關系。白利娟等[14]以刀尖為研究對象,利用振動輔助銑削獲得的仿真刀尖軌跡生成生物表面形貌,與實驗結果對比表明振動輔助銑削表面形貌在仿生表面的加工領域具有可行性。Lu等[15]基于微銑刀的實際切削軌跡和柔性變形建立了表面形貌仿真模型來預測表面粗糙度,并通過實驗驗證了模型的準確性。梁鑫光等[16]利用球頭銑刀刀刃的三維次擺線軌跡,通過等間隔的距離、時長分別讀取工件表面的殘留高度、刀具振動響應,實現了加工表面名義形貌建模與系統動態響應軌跡仿真。張國華等[17]采用金屬切削理論對橢圓振動切削過程和三維切削模型進行了分析,結果表明切削過程中相鄰兩轉之間不同的相位差特征值對最終表面形貌有著重要影響。Costes等[18]使用非接觸式位移傳感器測量出銑削過程中刀具的高頻振動信號,通過提取走刀步長和刀具中心點,建立了刀具變形的力學模型,從而獲取到工件的表面形貌特征。

以上研究工作盡管考慮了刀具的變形、振動等因素對銑削形貌造成的變化,卻沒有從夾具裝夾布局的角度研究工件加工表面形貌的形成規律。

本文首先根據工件與夾具的單向接觸這一實際條件建立裝夾布局的運動學模型,利用能量法推導出工件在銑削過程中的振動微分方程。然后提出振動微分方程的解耦方法,計算出工件位置的偏離。最后,建立周銑過程中切削刃的運動軌跡方程,結合工件位置偏離提出工件表面形貌的仿真方法。

1 裝夾布局的振動微分方程

在加工過程中,剛性工件將受到重力Fg、加工力Fc、扭矩Mc等外載作用。為抵抗這些外載的破壞作用,必須給工件施加夾緊力。

假設工件由m個定位元件定位后,施加n個夾緊力Fj(1≤j≤n)。將工件-定位元件等效為半彈性接觸模型,則第i個定位元件可以視為在法向ni=[nxi,nyi,nzi]T和兩個切向ti=[txi,tyi,tzi]T、ai=[axi,ayi,azi]T上忽略質量的阻尼彈簧,剛度和阻尼系數分別為kni、kti、kai和cni、cti、cai。記rw=[xw,yw,zw]T、Θw=[αw,βw,γw]T分別為工件坐標系Owxwywzw相對于全局坐標系Oxyz的位置和方向,如圖1所示。假定rw=[xw,yw,zw]T為工件上任意點P在Owxwywzw坐標系中的坐標,則P點在Oxyz坐標系中任意時刻的姿態為r=rw+T(Θw)rw,其中

圖1 工件振動模型

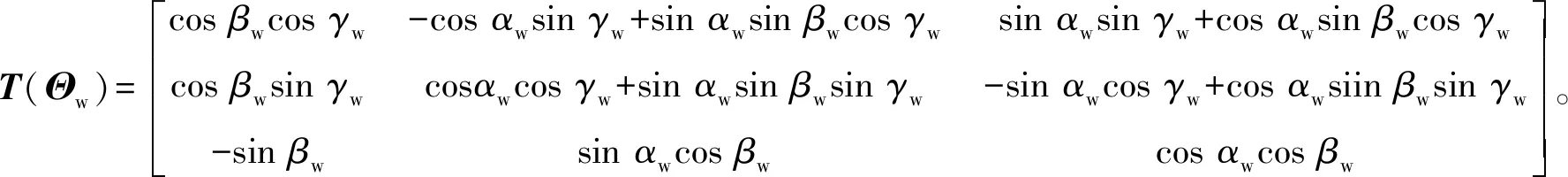
由此可以得到工件在裝夾布局系統中的振動微分方程[19],即

(1)

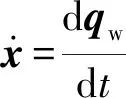
值得注意的是,工件裝夾的目的旨在給工件施加夾緊力,保證定位時獲得的工件相對于刀具的位置不變。為此,應使得式(1)中第i個定位元件的支撐反力滿足

(2)

為更簡單地描述式(2),采用矩陣形式進一步表達為

kNψdqw≥0

(3)

2 振動方程的解耦與求解

在個別情況下,M、C、K都是對角矩陣,這時式(1)的求解較為容易,但不具備普遍性。實際的加工過程中,振動系統的微分方程都會出現耦合項。因此,振動方程的解耦方法是解算工件位置偏移的關鍵。

2.1 振型向量的正交性

由式(1)可知,不考慮阻尼自由振動響應的表達式可以表示為

(4)

在系統的自由振動中,假設所有的質量均作簡諧運動,則方程的解可表示為

xs=A(s)sin(ωst+φs)

(5)

式中:xs表示第s階振型的諸位移的列陣;A(s)表示第s階振型中各點的位移最大值或振幅向量;ωs表示第s階振型的固有頻率;φs為第s階振型的相角。

將式(5)代入式(4)中,可得

(6)

由此得出對應固有頻率ωs和ωs的主振型A(s)和A(f)下述兩個方程式:

(7)

(8)

用(A(f))T左乘式(7),再轉置式(8)后右乘A(s),可以得到

(9)

(10)

這樣,由式(9)減去式(10),可得

(11)

(12)

當s≠f且特征值ωs≠ωf時,要滿足式(11)、式(12),必然有以下關系:

(A(f))TMA(s)=(A(s))TMA(f)=0

(13)

(A(f))TKA(s)=(A(s))TKA(f)=0

(14)

式(13)、式(14)表明,不相等的固有頻率兩個主振型之間存在關于質量矩陣M和和剛度矩陣K的正交性。

當s=f時,式(11)、式(12)對任何值都是成立的,使

(A(s))TMA(s)=Mps

(15)

(A(s))TKA(s)=Kps

(16)

式中:Mps和Kps分別為第s階的主質量和主剛度,均為常數,它們取決于特征向量A(s)是如何歸一化的。

將A(s)歸一化后依序排成各列,得到模態矩陣Ap,可表示為如下形式:

(17)

式中:λ為最大振型階數。

將式(17)代入式(15)、式(16),可得

(18)

(19)

式中:Mp和Kp分別為主質量矩陣和主剛度矩陣,兩者均為對角矩陣。

2.2 方程解耦

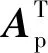
(20)

引用正交關系,將式(18)、式(19)代入式(20),可得

(21)

式中:

(22)

(23)

由于主質量矩陣Mp和主剛度矩陣Kp均為對角矩陣,利用主坐標描述系統的運動微分方程則不存在耦合。

(24)

(25)

式中:μs為一個待定常數,稱為正則化因子。

將式(25)代入式(24)中,可得

(26)

求出μs后代入式(25),得正則振型矩陣AN為

(27)

用AN按照式(18)計算得到的正則質量矩陣MN是一個單位矩陣I,即

(28)

又由式(7)、式(8)可知

(29)

(30)

(31)

對于具有阻尼為C的運動方程,正則阻尼矩陣CN可表示為

(32)

在實際工程應用中,大多數情況下CN都不為對角線矩陣,但工程上大多數振動系統中阻尼都較小,而且由于各種阻尼比較復雜,為使正則振型矩陣對角化,最簡單的辦法就是將其非對角線元素的值改為0,即

(33)

式中:CNss為第s階正則振型的阻尼系數。

在實際進行振動分析時,阻尼系數CNss通常用實驗或實測給出各階振型的阻尼比ξs。因此結合式(32),可得

(34)

2.3 方程求解

(35)

式(35)的解耦形式為

(36)

式中:1≤s≤6。

利用Duhamel積分可分別求解每一個主坐標,即

(37)

式中:t為系統時間;η為系統時間內任意時刻。

因此,振動微分方程的解為

dqw=ANXp
s.t.
kNψdqw≥0

(38)

3 刀刃運動軌跡

除工件的動態裝夾布局,影響工件加工表面形貌的另一大因素是刀具切削刃的幾何形狀。建模的關鍵點在于求解出刀刃在空間中的運動軌跡。

周銑過程如圖2所示,Oxyz、Owxwywzw分別為全局坐標系、工件坐標系,而Ocxcyczc、Osxsyszs分別為刀具坐標系、主軸坐標系。一般地,為方便起見,在建立坐標系時,應使Oxyz與Owxwywzw重合;R為銑刀半徑,γ為螺旋角,e為刀具偏心距,α為旋轉角度,vf為刀具進給速度,φj為第j個刀齒的初始角度,w為刀具轉速,刀具順銑時w取正值,逆銑時w取負值,P為切削點,ABCD為切削區域。

圖2 周銑切削刃運動示意圖

若刀具有z個刀齒,則第j個刀齒的初始角度可表示為

(39)

這樣,銑刀第j個刀刃上任意點P在Ocxcyczc坐標系的坐標應為

(40)

(41)

此外,在任意時刻t時,主軸沿進給方向y移動了vft。若在初始時刻Osxsyszs與Oxyz重合,則在t時刻,Osxsyszs相對于Oxyz坐標系的位置、方向分別為rs=[0,vft, 0]T,Θs= [0, 0, 0]T,則第j個刀刃上P點在Oxyz坐標系中的坐標為

(42)

4 工件表面形貌

對工件上任意一點的位置r進行求導可知,在t時刻,若工件由裝夾布局振動引起dqw的位置變化,則工件上任意一點的位置變化應為

dr=Edqw

(43)

式中:

(44)

則在t時刻,若刀齒上P點在切削區域ABCD范圍內沿背吃刀量方向上,則當且僅當P點坐標在理論切削平面與待切削平面之間,表明P點參與了切削,如圖3所示。圖3中ap為軸向切削深度。

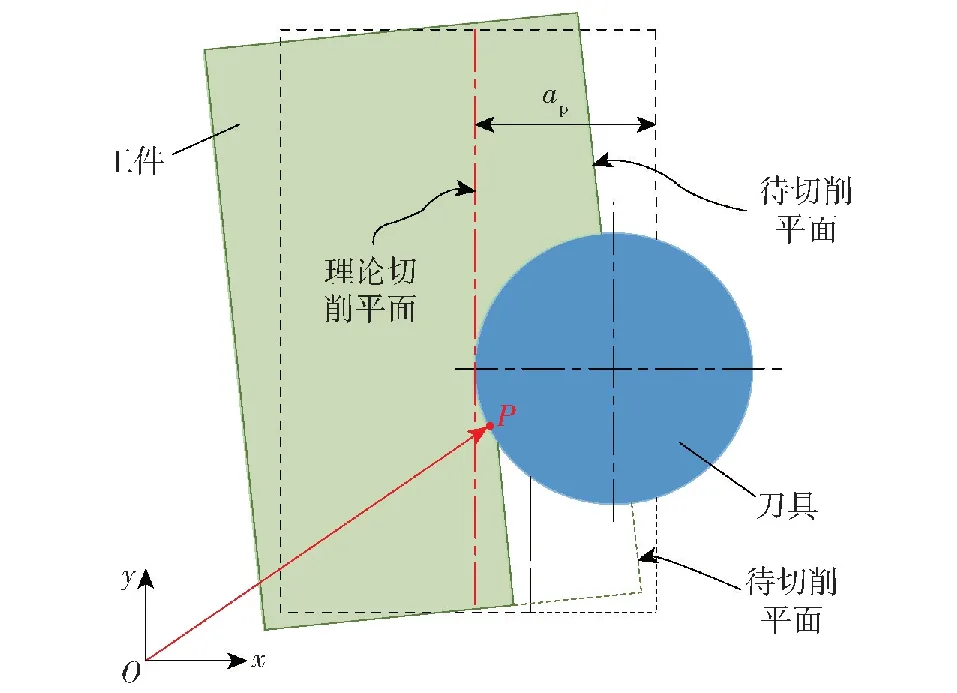
圖3 坐標平面Oxy內的表面成形示意圖

根據式(42)、式(43)可知,切削平面上P點的坐標rP=[xP,yP,zP]應為

(45)

式中:

(46)

顯然,式(45)很難求解處理,故采用離散方法進行求解。表面形貌離散算法步驟如下:

步驟1離散待切削平面。

分別以步長Δy、Δz將工件均勻劃分成m×n個網格,用矩陣存儲每個網格節點的坐標值分別為x(u,e)、y(u,e)、z(u,e),其中u=1, 2, …,m+1,e=1, 2, …,n+1。

步驟2離散切削時間和切削刃。

根據工件網格精度設置時間離散步長Δt以及切削刃離散點數l,一般取Δt=min{Δy, Δz}/(wR),l=hT/min{Δy, Δz},hT為銑刀切削部分的有效長度,以保證切削刃離散微元在加工平面內的投影不超過工件的網格間距,并且在單位時間步長內最多掃過一個工件網格點。

步驟3初始化切削時間t=0 s。

步驟4計算當前時間的裝夾布局振動。

根據式(43)獲得切削平面上每個網格節點的坐標r(u,e)=[x(u,e),y(u,e),z(u,e)]T。

步驟5初始化切削刃號j=1。

步驟6初始化離散點號k=1。

步驟7判斷離散點是否在加工區域內?

根據式(42),計算切削刃上離散點Pk在當前時間的坐標值(xk,yk,zk),并判斷其是否在待加工平面內。若是則轉步驟8,否則轉步驟10。

步驟8搜索離切削刃離散點最近的待加工平面網格節點。當離散點的位置(yk,zk)與網格點的位置(y(u,e),z(u,e))重合或者最接近時,該離散點與網格點相對應。

步驟9判斷切削刃離散點的切削情況。比較最近網格節點x(u,e)與切削刃離散點Pk的xk之間的關系,如果xk

步驟10判斷是否為最后一個離散點?若是則轉步驟11;否則計算下一離散點k=k+1,轉步驟7。

步驟11判斷是否為最后一個切削刃?若是則轉步驟12;否則計算下一個切削刃j=j+1,轉步驟6。

步驟12判斷是否為最后一個時刻?若是則結束計算過程,存儲的x(u,e)、y(u,e)、z(u,e)即形成切削表面形貌;否則計算下一個時刻,轉步驟4。

5 應用實例

采用兩個典型實例詳細說明表面形貌的計算,并驗證表面形貌計算結果的正確性。第1個實例將工件固緊在工作臺上,忽略裝夾振動帶來的影響,直接測量表面粗糙度值進行驗證;第2個實例來自于參考文獻[20],通過驗證接觸力大小間接驗證計算過程的有效性,并給出考慮裝夾振動的表面形貌。

5.1 不考慮振動的表面形貌

圖4為一立銑刀周銑工件的銑削實驗現場圖與實驗結果圖。工件的材料為鋁合金,楊氏模量Ew=207 GPa;刀具的材料為硬質合金,楊氏模量ET=530 GPa,其他參數如表1所示。由裝夾方案及刀具參數可知,刀具以及工件在周銑加工過程中的剛性都較強,因此忽略二者在加工過程中的振動。

表1 周銑加工參數

圖4 周銑實驗

不考慮工件裝夾布局在加工過程中對工件銑削表面形貌產生的影響,即dqw=0,單獨驗證周銑算法的有效性。

根據表1設置銑削加工參數。設Δy=Δz=0.05 mm,將銑削表面均勻劃分為120×120個網格。用矩陣x(u,e)、y(u,e)、z(u,e)存儲每個網格節點的坐標值。之后計算離散時間間隔Δt=min{Δy, Δz}/(wR)=9.55×10-5s,切削刃離散點數l=hT/min{Δy, Δz}=120。

由于不考慮工件振動,可以對表面形貌離散算法進行簡化,不考慮算法中的步驟4,經計算后得到表面形貌結果如圖5所示。

圖5 不考慮振動的表面形貌

圖6給出了在穩態加工情況下逆銑和順銑的實際加工表面。通過對比實際加工表面和仿真形貌結果可以看出,表面形貌離散算法的計算結果與實際加工情況非常吻合。

圖6 穩態加工中的實際加工表面(左為實際加工表面,中為黑白仿真表面,右為彩色仿真表面)

為進一步從數值上進行對比,在由中國上海精密儀器儀表有限公司生產的粗糙度輪廓儀JB-6CA上測量銑削表面的粗糙度,如圖7所示,測量結果如圖4(b)所示。將實測及計算結果的輪廓算術平均偏差Ra列入表2中。通過對比可知,逆銑表面形貌離散算法獲得的結果具有較好的準確度。

表2 周銑形貌仿真實驗驗證結果

圖7 粗糙度測量

5.2 考慮振動的表面形貌

采用半徑R=9 mm的銑刀,以軸向切深ap=3 mm、每齒進給量f=0.05 mm、銑削速度v=100 mm/min 在工件表面上銑槽[19-20],如圖8所示。圖8中,F1、F2為夾緊力,L0～L5為定位元件。工件的外形輪廓尺寸為220 mm×122 mm×112 mm,材料為7075-T6鋁合金,工件的楊氏模量和泊松比分別為Ew=70 GPa與bw=0.334;工件重力為Fgrav=[0 N, 59.73 N, 0 N]T,質心位置為rgrav=[110 mm, 56 mm, 61 mm]T,加工力和加工扭矩[20]分別為Fmach=[-131 N, -55 N, 232 N]T,Mmach=[0 N·m, 2.77 N·m, 0 N·m]T。

圖8 3-2-1裝夾方案

為保證加工過程的順利實現,分別在r1=[110 mm, 60 mm, 0 mm]T和r2=[220 mm, 60 mm, 60 mm]T處施加夾緊力F1= 640 N和F2=670 N。各定位元件的位置與單位法向量如表3所示。平頭定位元件由硬質鋼制造,定位元件楊氏模量和泊松比分別為Ef=207 GPa與bf=0.292,定位元件半徑Rf=6 mm,長Hf=12 mm,阻尼系數cf=7 000 N·s/m。

表3 定位元件的位置與法向量

根據工件質量、定位元件彈性模量等數據,容易得到剛度矩陣、質量矩陣、阻尼矩陣分別為

(47)

(48)

(49)

結合質量、剛度與阻尼矩陣及式(1)并解耦,可以得到6個2階微分方程,其中動態外載F(t)=[801 N, 114.73 N, -872 N, -9.1024 N·m, 22.08-0.3867tN·m, -0.091 7t-0.324 2 N·m]T,切削時間為0 s≤t≤132 s,根據式(37)可求得工件的位置偏移隨時間t的變化,結果如圖9、圖10所示。

圖9 不考慮阻尼的工件位置變化

圖10 考慮阻尼的工件位置變化

通過比較可以發現,考慮阻尼與不考慮阻尼兩種情況工件的位置偏移趨勢大致是相同。但不考慮阻尼時,工件位置偏離的變化是不穩定的;考慮阻尼時,工件位置偏離是穩定的。

由于工件位置的振動偏移是由各定位元件的位置偏移造成的,工件振動的計算值可通過測量定位元件處支承反力來間接保證。實驗裝置圖如圖11[20]所示。各定位元件處支撐反力的實驗測量值如圖12(a)[20]所示,靜力學模型計算值如圖12(b)[21]所示,根據式(3)計算出來的動態支承反力如圖12(c)所示,圖中標號0～5分別表示定位元件L0～L5。由圖12分析比較可知,定位元件處的支承反力靜力學模型計算值的誤差為15%[20],動力學模型計算值更接近于實驗結果,誤差約在12%以內,精度提高了3%。顯然,無論是支撐反力的變化趨勢還是力的大小,兩者均非常吻合。

圖11 實驗裝置

圖12 支撐反力

根據本文提出的表面形貌離散算法,選取槽的任一側面進行形貌仿真,經公式計算剛度G=πER2/H,式中H為定位元件長度,這時定位元件的剛度約為刀具的一半,因此主要考慮裝夾布局振動對表面形貌造成的影響,其結果如圖13、圖14所示。

圖13 逆銑形貌

圖14 順銑形貌

由圖13、圖15可以看出,不考慮裝夾布局和考慮裝夾布局的三維形貌大致相同。但不考慮裝夾布局時整體切削深度更深,這是因為工件是剛性的,考慮裝夾布局時工件振動會導致工件整體發生位置偏移。

圖15 截面輪廓對比

從表面質量的角度來看,在考慮裝夾布局對加工表面形貌的影響時,仿真表面明顯更為不平整。通過計算,不考慮裝夾布局時逆銑和順銑的輪廓算術平均偏差Ra分別為5.956 μm和6.358 μm,考慮裝夾布局時逆銑和順銑的輪廓算術平均偏差Ra分別為6.237 μm和6.549 μm,計算精度分別提高了4.72%和3.00%。

6 結論

1) 將工件與夾具之間的接觸模式等價為線性彈簧-阻尼系統,建立了工件裝夾布局模型。利用能量法建立了工件的振動微分方程,并根據加工過程中接觸力必須為壓力這一工況,利用胡克定律推導出了工件-夾具裝夾布局的單項接觸約束條件。

2) 根據機械振動學中的解耦方法,利用坐標轉化法提出在約束條件下振動微分方程的模態分析求解方法,以實現工件位置偏離的預測。

3) 基于運動齊次坐標的變換矩陣和矢量運算法則,建立了周銑切削刃的運動軌跡方程,給出了周銑加工表面形貌的離散仿真算法。

4) 在不考慮裝夾布局引起的工件振動的情況下,用實驗驗證了形貌仿真算法,逆銑和順銑粗糙度的相對誤差分別為5.52%和7.56%;在考慮裝夾布局的情況下,用支承反力驗證了定位元件位置偏移的有效性,模型的誤差大約在12%以內,與靜力學模型相比,精度提高了3%,并對兩種情況下的形貌進行了仿真對比。

5) 在實際加工過程中,若刀具切削部分較長,此時相較于裝夾方案,刀具振動對表面形貌的影響更為嚴重,這也是今后研究的重點方向。