活用多邊形外心確定多面體外接球的球心
黃 雨 顧 飛
(安徽省淮南第二中學)
球是高中立體幾何中非常重要的幾何體之一,也是最優美的空間幾何體之一.古希臘數學家阿基米德的墓碑上刻著球及其外接圓柱,這是其最得意的圖形,可見球是受到了大數學家的青睞.關于空間幾何體外接球和內切球的問題,是高中數學學習的一個難點.為了有效解決這一問題,一線數學教師構建了很多模型來解決球的問題,例如,墻角模型、漢堡模型、斗笠模型、切瓜模型等,通過構建不同的模型解決各種球的問題,但是模型太多,方法太雜.
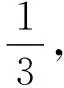
1.知識背景
1.1 球的性質
性質1:用一個平面去截球,其截面圖形是圓;
性質2:球心與截面圓圓心的連線垂直于截面;
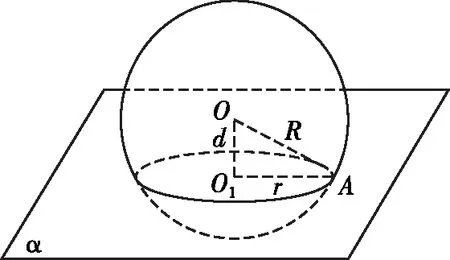
性質3:球的半徑為R,截面圓的半徑為r,球心到截面圓圓心的距離為d,則R2=d2+r2(如圖).
1.2 三角形外接圓
外接圓圓心:三角形三邊中垂線的交點即是三角形外接圓圓心,簡稱外心.
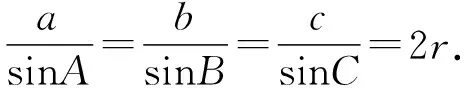
2.知識深化
由性質1可知,O1就是多邊形的外心.
由性質2可知,OO1⊥平面O1,反過來,過O1且垂直于平面O1的直線一定經過球心O.那么,我們選取兩個截面,分別過兩個截面的圓心O1,O2,作各自平面的垂線,則這兩條垂線的交點就是球心O,如圖1.
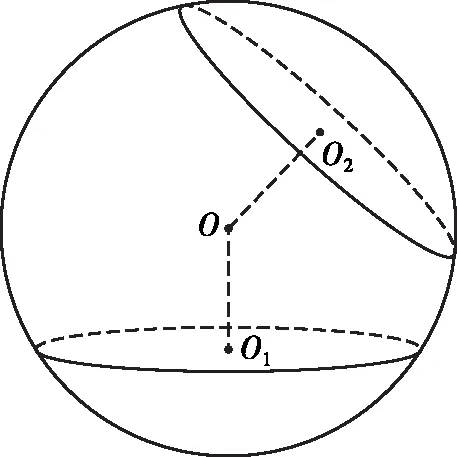
圖1
凝練:選取多面體的兩個平面,找兩個面多邊形的外心,分別過兩面多邊形的外心作各自面的垂線,兩垂線的交點是球心.
特殊情況:
推論一:如圖2,如果兩面多邊形的外心重合,那么這個外心就是球心.
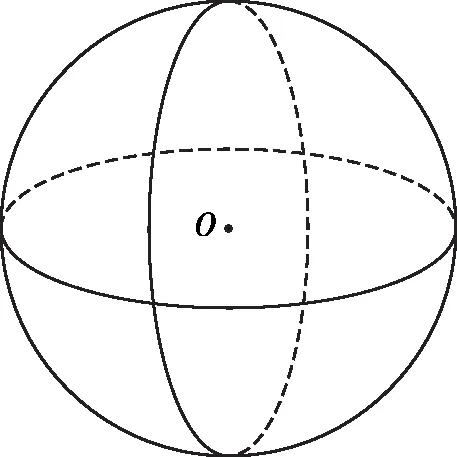
圖2
推論二:如圖3,如果過一個面外心的垂線經過另一個面的外心,那么另一個面的外心就是球心.
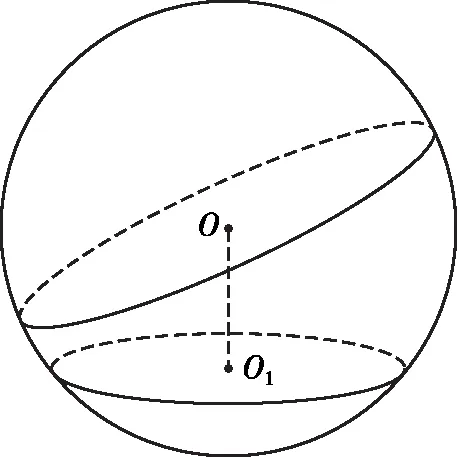
圖3
3.知識運用
3.1 特殊情況1
【例1】中國古代數學專著《九章算術》系統地總結了戰國、秦、漢時期的數學成就.書中將底面為長方形且有一條側棱與底面垂直的四棱錐稱之為陽馬,將四個面都為直角三角形的三棱錐稱之為鱉臑.如圖為一個陽馬與一個鱉臑的組合體,已知三棱錐P-ADE為鱉臑,且PA⊥平面ABCE,AB=AD=2,ED=1,該鱉臑的外接球的表面積為9π,則陽馬的外接球的體積為
( )
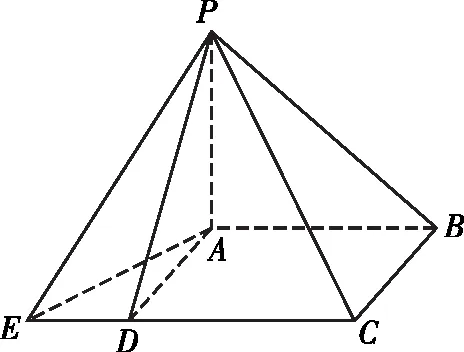
【答案】D
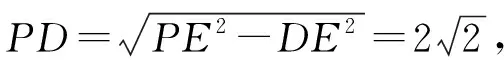
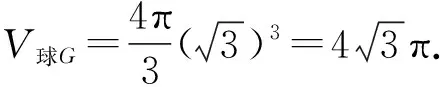
【注】本題滿足推論一,可以直接確定球心的位置.
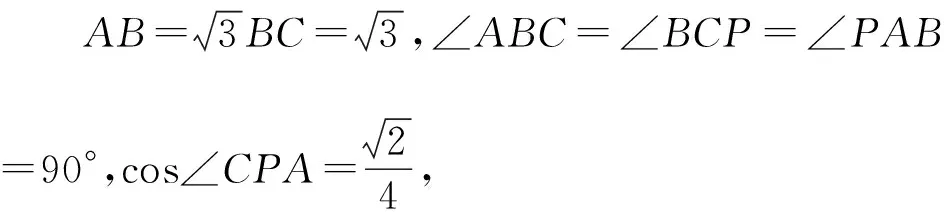
( )
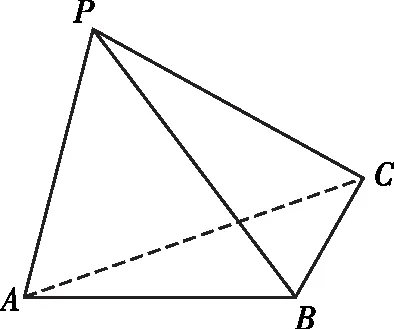
A.5π B.13π C.6π D.14π
【答案】A
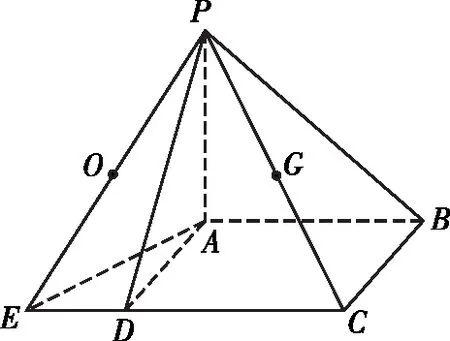
【解析】由題意得△PAB,△PCB均為直角三角形,則外心均為PB的中點,故PB即為三棱錐P-ABC的外接球的直徑.
設PA=a,PC=c,
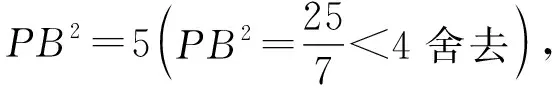
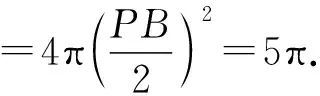
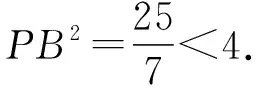
3.2 特殊情況2
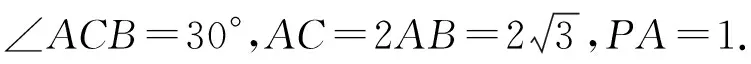
( )
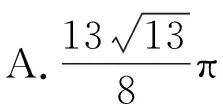
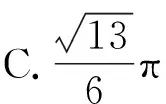
【答案】D
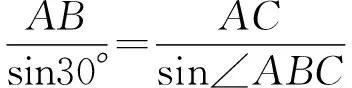
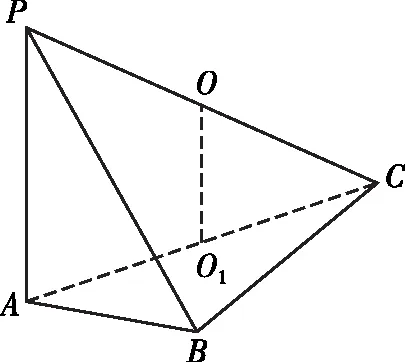
【注】本題滿足推論二,過一個平面的外心O1的垂線經過另一個平面的外心O,這個外心O即為球心.特別注意,作平面的垂線一定要有參考線,本題參考線是PA.
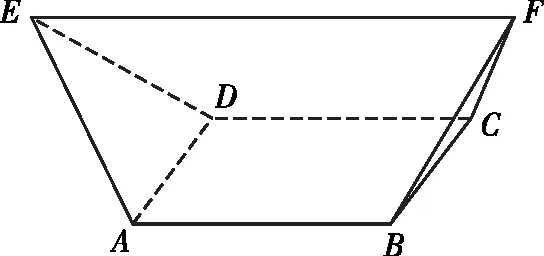
【例4】(2021·A10聯盟高二上學期開學聯考)如圖,在幾何體ABCDEF中,底面ABCD是正方形,EF∥平面ABCD,EF=4,其余棱長都為2,則這個幾何體的外接球的體積為
( )
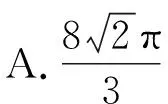
【答案】D
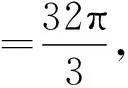
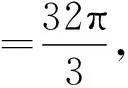
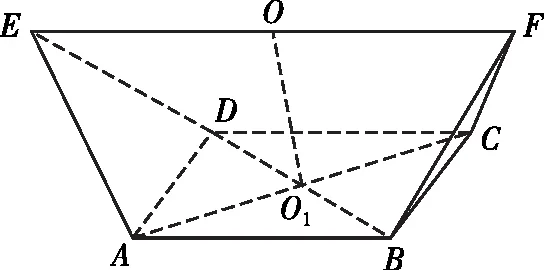
【注】本題可以采用兩種特殊情況來快速解決,也可以采用一般情況來解決,下文我會詳細介紹一般情況的解決方法.等腰梯形、正方形的外心也是我們所熟知的內容,要根據邊長關系確定其外心的位置.
3.3 一般情況
對于一般情況,需要確定兩個平面多邊形的外心,過外心分別作各自平面的垂線.那么這兩個面的選取要有可行性,要能確定其外心及垂線的位置.
( )
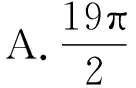
【答案】A
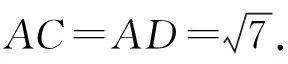
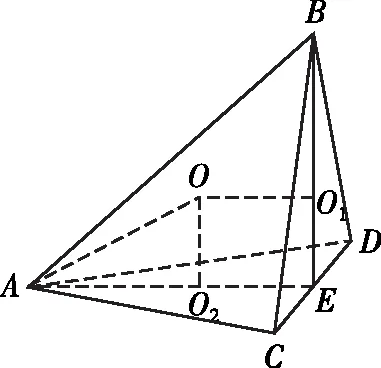
【注】選取的兩個平面圖形要滿足兩個條件,一是能夠確定外接圓圓心的位置及半徑,二是作垂線時要找到與平面垂直的直線作為參考線,這樣作出的垂線才能求解.本題稱為切瓜模型,我們拋開模型,從球的性質出發,仍能很好地解決.
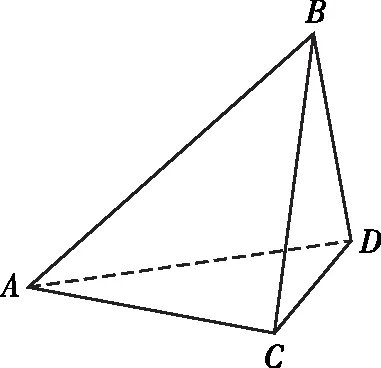
【例6】(《立體幾何的秘密》 蘇立標 編著)如圖,已知正方形ABCD的邊長為4,E,F分別是AB,BC的中點,將△ADE,△EBF,△FCD分別沿DE,EF,FD折起,使得A,B,C三點重合于點A′.若點G及四面體A′DEF的四個頂點都在同一個球面上,則以△FDE為底面的三棱錐G-DEF的高h的最大值為
( )
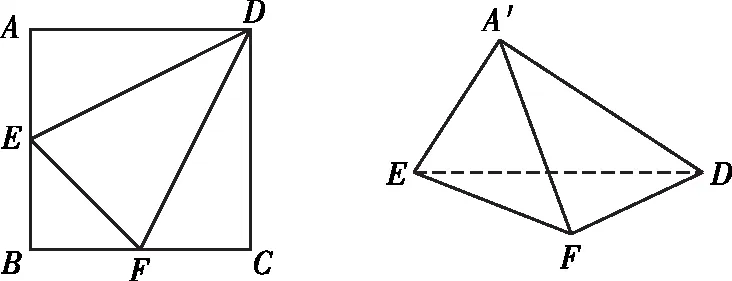
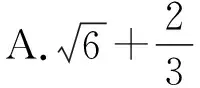
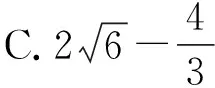
【答案】A
【解析】解法一:設外接球的球心為O,球的半徑為R,折疊后滿足墻角模型.
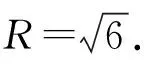
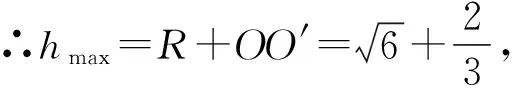
解法二:如圖,過△A′EF的外心O1作A′D的平行線,過△A′DF的外心O2作A′E的平行線,兩線交于點O,點O即為外接球球心.
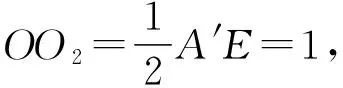
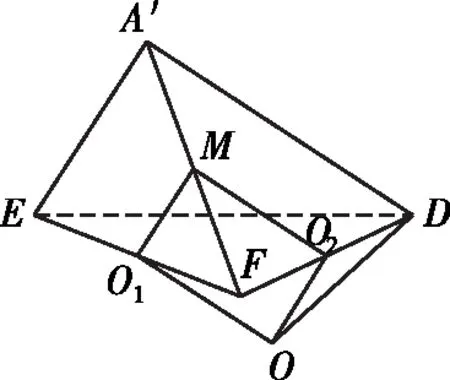
【注】本題可用墻角模型來解決.我們也可以拋開模型,就從球的基本性質出發,牢牢抓住本質,反而更有利于學生對知識的理解.
4.知識總結
4.1 淡化模型教學,注重知識本質
立體幾何的教學離不開實物或模型,空間想象也不是憑空產生的,都是在實物或模型的基礎上抽象出來的.但是我們不能只認識實物或模型,實物或模型總是有限的,而空間幾何體是無限的、千變萬化的.要使同學通過對有限實物或模型的觀察、體驗,抽象出對于一般幾何圖形的空間觀念.
模型化的解題通常是一題一法,不利于學生對知識本質的理解,教師教學中一定要抓住球的本質屬性,強調通性通法,力求用最本質的方法解決更多的問題.
4.2 平面多邊形的選取一定要有可行性
第一,選取的平面多邊形的外心能夠確定位置.可以選取直角三角形、等邊三角形等特殊多邊形,如果是一般三角形,可以選取邊角等元素已知的三角形,方便確定外接圓圓心的位置.

(本文系2021年度安徽省教育科學研究項目《基于數學實驗課程建設下的高中生數學學習品質的培養與評價研究》編號(JK21099)的階段性研究成果)

