利用衍生特征預測新冠疫情的隨機森林方法

龍 鐵,付宇笙,王文達,費 寧

(南京郵電大學 計算機學院,江蘇 南京 210003)

0 引 言

隨機森林[1-2]是一種機器學習算法,相較于決策樹,能很好地防止過擬合;在面對高維復雜的數據時,能較好地容忍噪聲值和離群值[3];同時由于它實現簡單,學習速度快,在天氣預報、疾病分析、圖像識別等眾多領域都得到了應用。當下新冠肺炎病毒具有高傳染性和高隱蔽性的傳播特性,產生的疫情數據繁多復雜。在分析原始新冠疫情數據的基礎上,該文通過衍生出新的關鍵特征值,對原本不均衡的數據集分組使用隨機森林進行新冠疫情發展趨勢的預測,從而有效提高整體的預測準確率。

1 相關研究

當前已經有許多方法用于新冠疫情的預測。常用的預測方法概括為兩大類:(1)基于傳統模型的預測;(2)基于機器學習的預測。

基于傳統模型的預測方法主要包括:倉室模型[4](SIR和SEIR等)、時滯動力學模型[5](TDD-NCP等)。在通常的傳染模型中,通過人群間相互轉移的傳播學機制建立常微分方程組來描述疫情的發展,建立倉室模型。時滯動力學模型在構建時考慮潛伏期對于傳播時間的滯后效應,實際數據的擬合值與預測值在傳播初期較容易吻合。此類模型對于特定地區有著很好的擬合效果,但不同國家疫情環境不同,比如人口密度、隔離措施、醫療條件等,換一個地區往往既有模型難以適應,需要重新調整,工作較為復雜。

基于機器學習的預測方法主要包括[6]:線性回歸(Linear Regression,LR)、回歸模型(Least Absolute Shrinkage and Selection Operator,LASSO)、支持向量機(Support Vector Machine,SVM)、指數平滑法(Exponential Smoothing,ES)以及隨機森林(Random Forest,RF)等。其中隨機森林能夠比較好地適應高維度數據,具備較好的抗噪音能力以及免特征選擇等優點,更適合預測新冠疫情發展趨勢。在實驗過程中發現,隨機森林雖然能夠對所選新冠疫情數據集合做出較好的擬合和預測,但由于疫情數據各地區差異較大,回歸樹進行判決時無法選擇最優閾值,從而犧牲了判決的準確率。

在對現有傳統模型和機器學習方法研究比較后發現,大多數研究更重視算法本身的應用和性能比較,卻忽視了對現有數據的預處理。不同數據樣本個數和特征差異巨大,其中不乏重復甚至錯誤的特征存在。對于這樣的數據,進行適當的預處理比如降維或者增加衍生特征會明顯提高預測的準確性。這正是本研究的切入點和主要貢獻所在。該文使用一種在原有樣本的特征值上進行變換和組合的方法,增加了新的特征值。對于差異較大的特性,通過篩選出異常數據并單獨進行訓練,從而更好地處理了異常數據干擾的問題,得到了較好的泛化性能。

2 設計思路

2.1 CART回歸樹和性能指標

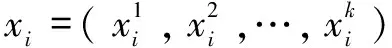
(1)

使用均方誤差(Mean Square Error,MSE)最小化得到的最佳參數:

(2)

給每個葉子節點賦予相應的預測值:

(3)

其中,

(4)

式(4)中的∏為布爾類型,若樣本落入區域則取值為1,若樣本沒有落入區域則取值為0。

遍歷樣本中所有的特征值和不同分割點,使得式(3)中平方誤差最小時,則回歸樹訓練完成。

回歸樹的評價指標包括平均絕對誤差MAE1(Mean Absolute Error)和最大絕對誤差MAE2(Max Absolute Error)[8]:

(5)

(6)

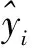
2.2 隨機森林集成學習模型

隨機森林是采用2.1節所示的CART回歸樹作為基本分類器的一個集成學習模型,包含多個由Bagging集成訓練得到的決策樹。預測過程如圖1所示。

輸入樣本數據后,根據閾值訪問下一個子節點,到葉子節點處結束,將所有葉子節點返回的決策樹預測值求平均得到該樣本的預測值。

CART回歸樹訓練子集的方式是有放回的抽樣,并且每個子集的樣本數量必須和原始樣本數量一致,但是子集中允許存在重復數據。CART樹還對原始數據集上的特征屬性進行隨機采樣,但采樣的屬性集是原始特征集的子集。

2.3 數據預處理和特征值選取

該文采用源于GitHub上的Johns Hopkins大學系統科學與工程中心提供的美國疫情相關數據[9-10],并從中人為選取了部分特征,去掉了一些冗余信息。表1列出了該數據集的數據類型和特征。

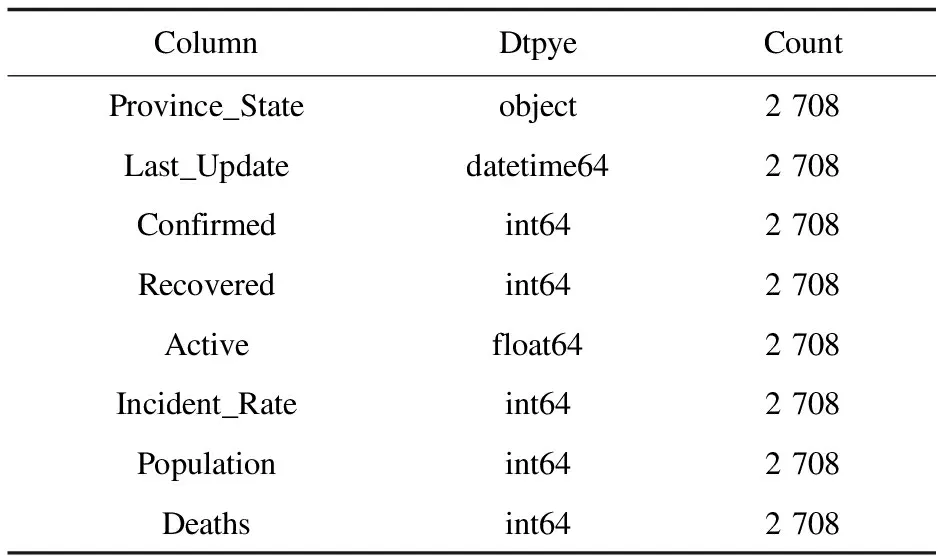
表1 Johns Hopkins新冠數據集特性

其中,Province_State是美國的州名,Last_Update是前一天數據更新的時間,Confirmed是累計確診人數,Recovered是累計治愈人數,Active是現階段的確診人數,Incident_Rate是傳染率,Population是州人口數,Deaths是累計死亡人數,Dtype表明數據類型。實驗時間范圍是2020年9月2日至2020年10月27日,共56天。樣本共有2 708例。

原始數據中的Province_State和Last_Update對預測沒有實際意義,Deaths也可以從Confirmed和Recovered中推算出來,不是一個獨立變量。基于此,從清洗后的數據集中選取以下五個特征,如表2所示。

表2 隨機森林實驗特征值集

3 實驗與分析

3.1 數據集的劃分

數據集一般劃分為訓練集和測試集,訓練集用于訓練模型,測試集用于檢驗模型的效果。在模型建立的過程中,由于采用的數據跟時間有明顯的相關性,因此以數據更新時間(Last_Update)作為組別,對數據按照留一組(leave-one-group-out)的方法來劃分訓練集和測試集[11],劃分過程如圖2所示。

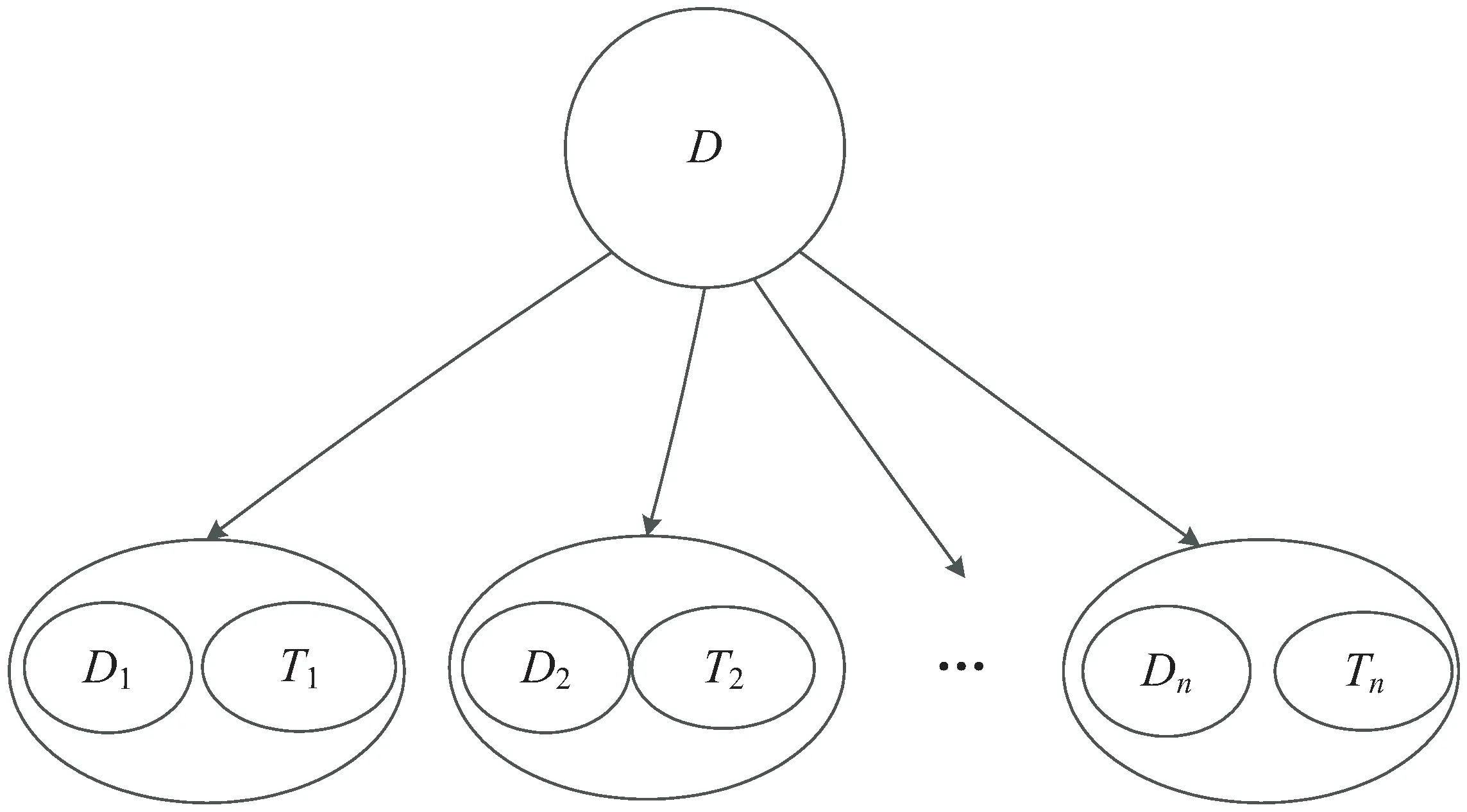
圖2 數據劃分

其中,D是原始數據集,D1是劃分出來的第一個訓練集,T1是劃分出來的第一個測試集,D1中包含了除T1所在日期外的所有樣本,T1中僅有一天的樣本。如此反復,對原始的數據集進行多次劃分,直到所有可能的訓練集和測試集劃分完畢。劃分出來的訓練集和測試集用于調整參數的交叉驗證。

模型建立之后,需驗證機器學習的效果,在此過程中,訓練集則采用56天中的前49天進行訓練,選取最后7天作為測試集進行驗證。

3.2 模型的建立

表3列出了初始構建隨機森林模型使用的參數。

表3 隨機森林部分參數

依據表3的隨機森林參數,獲得的擬合結果如圖3所示。其中橫坐標代表天數,縱坐標代表美國的總死亡人數,可以明顯地觀察到訓練集前49天實際值和擬合值基本吻合,有著較高準確度。49天以后的實際值和預測值偏差較大,呈下降趨勢。

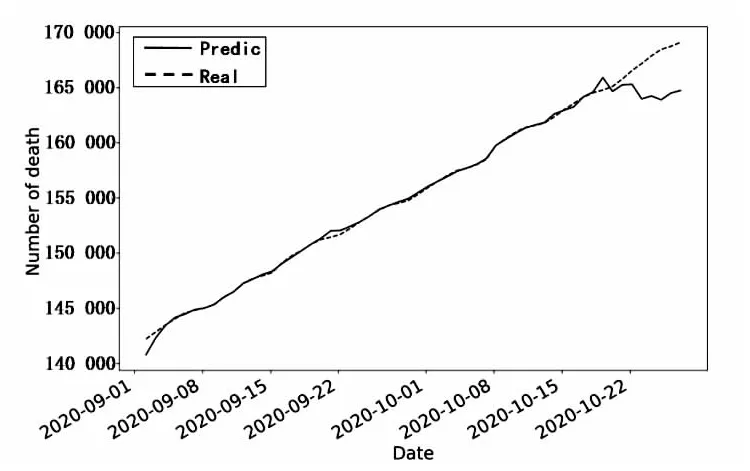
圖3 模型未調參的結果

常用的超參數優化方法有Grid Search[12](網格搜尋)和Random Search[13](隨機搜索)。由于隨機搜尋的優化效果不穩定,該文采用Grid Search進行調參,對每一組的數據進行嘗試,確保得到最佳超參數組合。

通過總結天津職業技術師范大學漢語國際教育專業極參與人文社科類學科競賽的經驗教訓，成敗利鈍，可以看出，人文社科類學科競賽對衡量文科專業的教學質量而言是非常重要的量化標準，對于提升學生思想道德水平和人文素養、實施社會主義核心價值觀教育更具有潛移默化的涵養作用。積極組織、引導、培訓文科學生參與到各層次的學科競賽活動之中，有利于以教學相長的方式推動教學改革工作，提升教學質量，也能有效促進高校的思想政治教育的改革與發展。如何繼續長效推進思想政治教育與人文社科類學科競賽的緊密結合，完善工作和激勵機制，發揮其更大的平臺輻射作用，是目前我們繼續思考和探索的重要課題。

從調參之后的結果圖可以看出,調參的效果不明顯,在49天之后的擬合效果偏差仍然較大。這表明隨機森林模型對訓練集匹配良好但與驗證集差距明顯且參數調優效果不佳。該預測結果表明,訓練過程可能出現了過擬合或者現有的數據集并沒有遵循特定趨勢。

為了驗證是否出現了過擬合的情況,將原訓練集進一步劃分為訓練集和測試集,測試集為訓練集的子集,并且子集中的樣本為原訓練集中隨機抽取的樣本。對新的訓練集和測試集用隨機森林進行學習和驗證,學習曲線如圖4所示。

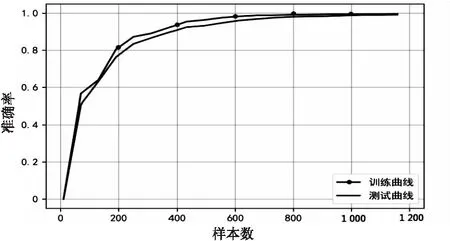
圖4 隨機森林學習曲線

圖中,橫坐標代表學習的樣本數,縱坐標代表驗證時的準確率。在樣本數達到1 200時,測試曲線基本擬合訓練曲線,并且無論是測試集或者是訓練集都與實際數據有著比較好的吻合效果,這表明模型學習效果良好,因此在該樣本集合上的過擬合的可能性較低。

3.3 差異化處理

針對圖3建模后49天擬合效果偏差較大這個問題,進一步從數據樣本分析原因。數據分布如圖5所示,從樣本特征值分布圖看出,少部分樣本集中在高人口,高死亡和高確診分布,部分樣本呈現相近確診,相近人口,但死亡人數差距大的復雜情況。由此該研究提出差異化處理。

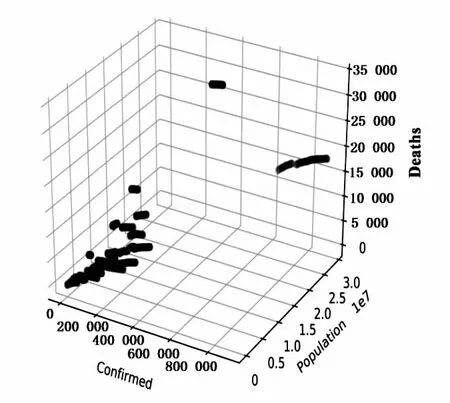
圖5 樣本特征值分布

根據隨機森林得到的特征重要性[14-15]如表4所示。

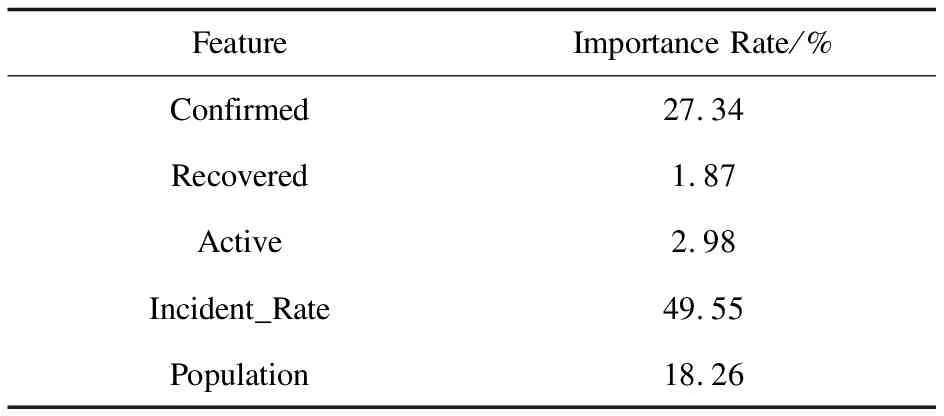
表4 特征重要性

可以發現,累計確診患者數(Confirmed)和州人口數(Population)的重要性最為顯著。表明回歸樹在劃分子節點的過程中,較多使用這兩個特征進行劃分,因此隨機森林對這兩個特征的依賴性強。能夠判斷若兩個州在累計確診患者數(Confirmed)和州人口數(Population)兩個特征相似的情況下,擁有差異顯著的死亡人數d1和d2,回歸樹在訓練過程中,會將這兩個州劃分到一個葉節點中,從而輸出平均預測值r,r在d1和d2的影響下,只能折中為d1和d2的平均值。因此,r無論是對于d1或者是d2而言都具有很高的偏差,從而造成測試集中出現高偏差的情況。

出現以上情況的原因可以歸為美國各州的醫療能力不同,地區環境不同,每一天的防控情況不同,因此,部分確診人數和州人口數近似的地區之間在死亡人數上有巨大差異。此時,需要一個衡量醫療能力的指標,來體現出差異性,并作為特征值供隨機森林模型學習訓練,從而降低誤差,最后達到泛化處理誤差的效果。

該文將死亡率作為衡量每個樣本醫療能力的指標,死亡率(Death Rate)定義如式(7)所示:

(7)

其中,Rd代表死亡率,D代表死亡人數,C代表確診人數。根據每一個樣本的死亡率劃分醫療能力等級,不同死亡率的樣本對應醫療能力等級范圍為1到n。為了確定最佳劃分的等級個數n以及使最佳等級劃分閾值t1,t2,…,tn誤差最小,采用迭代劃分的方法遍歷每種組合,尋找最優解。等級個數n取值范圍為1到k,k為樣本總個數。當n=k時,表明每個樣本的醫療能力等級都不同,可以直接使用每個樣本的死亡率作為衡量防控能力的指標進行劃分。

圖6是部分不同的n值(2～49)對應平均絕對誤差MAE1以及最大絕對誤差MAE2的取值。在圖6中,為了使MAE1的變化更加直觀,將MAE1放大了10倍。可以發現,在等級個數為39時,得到的MAE1和MAE2最小,因此確定最優劃分等級個數為39。

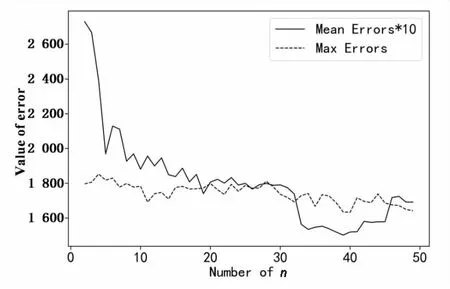
圖6 取不同n值時MAE1*10和MAE2的取值

根據劃分出來的最優等級個數39,將數據集劃分成39份D1,D2,…,D39,每一個子數據集對應一個防控等級,對每一個子數據集建立相應的隨機森林,將建好的隨機森林進行訓練。對于新輸入的測試數據M采取以下步驟方法進行預測:

(1)取最接近M時間的訓練集中的k個樣本(在本例中k為州的個數),作為一天的各個州的數據。

(2)將M的州和k個樣本中的州進行逐一比對,找出和M的州匹配的樣本S。在實驗中州匹配可以由州名直接確定或者由人口數據直接匹配,所以步驟1可以忽略。

(3)確定M的醫療防控能力等級和S的醫療防控能力等級相同,并將該等級作為M的醫療防控能力等級。

(4)用對應的隨機森林來對M進行預測得到死亡人數。

采用n=39的情況對模型進行誤差處理,最終的擬合結果如圖7所示。

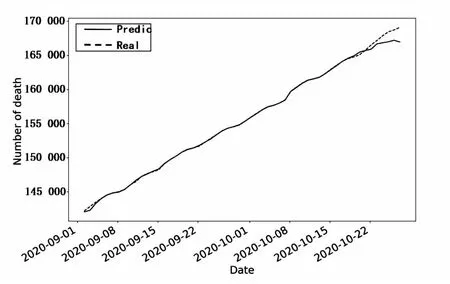
圖7 引入衍生特征處理后的擬合結果

對比圖3和圖7可以發現,在引入衍生特征差異化處理調整參數后,該預測方法兼顧了樣本的地區差異性和時間差異性,因此能夠起到大幅減小誤差的效果。直觀地表明樣本地區差異和時間差異的問題得到了較好解決。

4 結束語

運用隨機森林對疫情數據進行了擬合預測,通過對原始數據樣本進行變換衍生出新的特征值來更好地區分樣本,起到縮小隨機森林預測泛化誤差的效果。在對新冠疫情趨勢的訓練過程中發現,由于各個州之間發展不均衡,醫療條件相差巨大,無法作為一個整體進行預測。在對原始數據分析的基礎上,衍生出死亡率作為州醫療條件和防控能力的評價標準,并以此對數據進行分類并單獨建立隨機森林分類學習。在預測新樣本的死亡數時,選用訓練地區相近和時間相近的隨機森林對新樣本進行預測,兼顧了各州原有醫療能力的差異和采取不同防控措施引起的疫情發展的差異,對于其他類似的疫情預測和相近數據的差異化預測具有一定的參考意義。