基于改進灰狼算法的充電樁供電線路規劃研究

戰彥君,張玲華,2

(1.南京郵電大學 通信與信息工程學院,江蘇 南京 210003;2.江蘇省通信與網絡技術工程研究中心,江蘇 南京 210003)

0 引 言

近年來,煤炭、石油、天然氣等化石燃料的大量消耗,使得能源危機和環境問題日益嚴重[1]。為了有效應對,中國提出了碳達峰、碳中和目標,致力于構建以電能為核心的清潔、低碳、高效能源體系,大力推廣電動汽車是其中的重要一環。與燃油汽車不同的是,電動汽車續航能力較差,因此要在城市中布設充電樁。由于實際城市中建筑的限制以及區域需求不同,充電樁的分布具有隨機性和不均勻性,假如充電樁和電力調度中心之間供電線路規劃不合理,必然會大大增加建設成本和電力傳輸過程中的損耗。為此,研究合適的充電樁供電線路模型,以最高效率和最低成本對充電樁供電十分重要。

受到灰狼圍捕和狩獵的行為啟發,Mirjalili等人于2014年提出了灰狼算法[2](gray wolf optimization,GWO)。相較于粒子群算法[3]、遺傳算法[4]、蟻群算法[5]等經典智能優化算法,該算法具有結構簡單、參數少、求解精度高且速度快[6]等優點,被廣泛應用于經濟調度[7]、作業車間調度[8]、圖像分割[9]和云計算資源負荷預測[10]等諸多領域。但是,GWO算法存在易陷入局部最優解、初始種群分布不均勻和后期收斂速度慢[11]等缺點。該文提出一種基于Tent混沌映射[12]和自適應收斂因子的改進灰狼優化算法(ITAGWO),將其應用于城市電動汽車充電樁供電線路規劃中。首先,針對初始種群分布不均勻,采用Tent混沌映射來產生種群初始可行解,以豐富種群的多樣性;其次,將線性收斂因子改為非線性自適應收斂因子,平衡其局部搜索和全局搜索能力,加快收斂速度;最后,改進灰狼圍捕獵物時的位置更新公式,以不同權重采納三類頭狼的經驗,并加入隨機擾動因子。對區域的充電樁進行供電線路規劃仿真,與傳統灰狼算法、粒子群算法(particle swarm optimization,PSO)、遺傳算法(genetic algorithm,GA)、免疫算法[13](immune algorithm,IA)、模擬退火算法[14](simulated annealing algorithm,SA)、布谷鳥算法[15](cuckoo search algorithm,CSA)、教與學算法[16](teaching-learning-based optimization,TLBO)進行了對比。在到達全局最優解的前提下,該算法迭代次數少、收斂速度快且穩定性好,相比于其他智能算法具有明顯優勢。

1 模型構建

該文主要提出一種充電樁供電線路規劃模型,在連接區域中所有充電樁的同時,以路徑最短為目標。模型可以描述為:在區域中有n個充電樁,并且充電樁坐標位置已知,供電線路從其中某一充電樁出發,依次為區域中所有充電樁輸電,每個充電樁都只被經過一次。當區域中充電樁數目過多時,單線路輸電效率過低,此時將區域分成多個子區域,每個子區域采用一條供電線路將區域內的充電樁遍歷,可以顯著縮短供電時間,提高充電樁輸電效率。為構建適當模型,作以下假設:

(1)不考慮實際的交通道路情況,僅以直線距離為例;

(2)不考慮線路中僅有部分充電樁需要供電的情況,假設每次輸電每個充電樁都需要被充電;

(3)假設電力調度中心距離哪個充電樁近,就以該充電樁為起點;

(4)不考慮充電樁需求量超過線路輸送容量的情況,假設每次輸電都能滿足所有充電樁的需求;

(5)當劃分子區域時,假設各子區域中的供電線路都與單調度線路模型一致。

1.1 單調度線路模型構建

(1)區域中第i個充電樁和第j個充電樁之間的距離Dij的計算公式為:

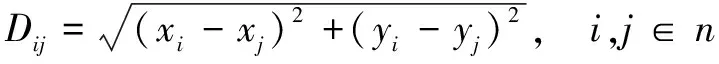
(1)

其中,xi和yi表示充電樁i的橫縱坐標;xj和yj表示充電樁j的橫縱坐標;n表示區域中的充電樁個數。

(2)定義0-1變量來判斷是否經過某個充電樁:

(2)

(3)為了以最小運輸成本給充電樁輸電,就要使供電線路的總路徑長度最小,所以目標函數的函數表示為:

(3)

其中,約束條件表示調度線路必須經過每個充電樁,并且只經過一次。

1.2 多調度線路模型構建

當區域中充電樁數量過多時,為了有效提高輸電效率,將區域劃分成多個子區域,分多條線路對供電樁進行高效率輸電。在充電樁總數為n的情況下,將區域分成p個子區域,第k個子區域中的充電樁個數為xk(k=1,2,…,p)。

(1)在第k個子區域中,第i個充電樁和第j個充電樁之間的距離Dikjk計算公式為:

(4)

其中,xik和yik表示第k個子區域中充電樁i的橫縱坐標;xjk和yjk表示第k個子區域中充電樁j的橫縱坐標。

(2)定義0-1變量來判斷是否經過第k個子區域中某個充電樁。

(5)

(3)要遍歷子區域中的每個充電樁,同時供電線路總長度最短,目標函數表達式為:

(6)

其中,p表示所劃分的子區域個數;xk表示第k個子區域中充電樁的個數;約束條件表示第k條供電線路必須經過子區域k中每個充電樁,且只經過一次,所有子區域中充電樁總數為m。

2 傳統灰狼算法

2.1 灰狼種群的等級制度

灰狼種群具有十分嚴格的等級制度,狼群具體劃分為α狼、β狼、δ狼、ω狼四類[17]。其中α狼是種群中的最高領導者,負責管理種群和各項重要決策事務;β狼的職責是協助α狼做出決策和管理整個種群,傳送上級指令并反饋信息;δ狼服從前兩類狼的調度命令,從事偵查、放哨等底層管理事務,能力不足或者生病的α狼、β狼也會降級成δ狼;而ω狼是種群的基本組成成員,等級最低且數量最多,需要服從三類頭狼的命令,對于維持種群平衡有著不可或缺的作用。

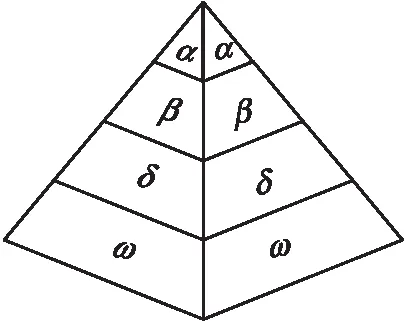
圖1 灰狼種群等級金字塔

灰狼狼群的捕獵行為分成跟蹤、包圍和獵殺三個階段。首先,灰狼群體會對目標獵物進行追蹤;之后,由α狼帶領整個狼群對目標獵物進行全方位的包圍;最后,α狼指揮最靠近獵物的β狼、δ狼對獵物進行獵殺,若是獵物逃脫,由狼群中其余灰狼繼續進行圍獵,直到最終捕獲獵物。

2.2 灰狼算法GWO

假設搜索空間為D維,數量為N的灰狼組成種群,其中第i只灰狼的位置記為:Xi=(Xi1,Xi2,…,XiD),將種群中適應度值前三個分別記為α狼、β狼和δ狼,種群中其它個體全部記為ω狼。

(1)在跟蹤和包圍獵物的過程中,相應的數學模型為:

(7)

(8)

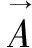
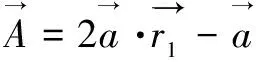
(9)

(10)

(2)在狼群鎖定目標獵物的位置后,α狼會帶領β狼和δ狼包圍獵物。通常這三類狼對目標獵物的潛在位置更加了解,所以狼群其他成員根據三者的位置判斷獵物的位置并不斷更新自身位置,向著目標獵物靠近。狼群圍獵行為的數學模型如式(11)～式(13)所示:

(11)

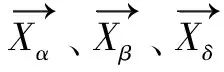
(12)

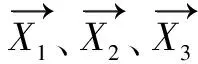
(13)

根據式(13)所求步長,最終確定灰狼個體下一步的更新位置。

3 改進灰狼算法(ITAGWO)

3.1 Tent混沌映射

針對GWO隨機產生初始可行解導致的初始種群分布不均勻、物種多樣性差的缺陷,采用Tent混沌映射的方法產生初始種群,其良好的多樣性和遍歷性有效提高了求解精度和收斂速度。Tent映射也即帳篷映射,是一種分段的線性映射,因其函數圖像酷似帳篷而得名,其函數表示如下:

(14)

由于u=1/2時,Tent映射是具有均勻分布的典型序列,對不同的參數有近似一致的分布密度,因而該文引用u=1/2的Tent映射公式,如式(15)所示:

(15)

3.2 非線性收斂因子

在灰狼算法中,收斂因子a的選取決定算法的局部和全局搜索能力[18]。傳統灰狼算法的收斂因子是從2線性遞減到0的,而在實際優化問題中灰狼算法的搜索過程比較復雜,線性遞減的收斂因子導致算法的搜索能力弱[19]。該文采用非線性遞減的方式改進收斂因子[20]:前期遞減速度慢,較大的a值增強全局搜索能力,避免陷入局部最優解;后期收斂速度慢,較小的a值增強局部搜索能力 ,加快收斂速度。這種非線性收斂機制可以協調灰狼算法的局部和全局搜索能力,并且a值切換具備自適應性。改進收斂因子表達式如式(16)所示:

(16)

其中,k為調節系數,它的取值決定著a隨著迭代次數增加而遞減的速度,該文取為e[6];t為當前迭代次數;tmax為最大迭代次數。

3.3 隨機擾動

傳統灰狼算法中,ω狼的位置更新是等權重地參考三類頭狼的位置信息,在搜索后期所有灰狼都會向α狼、β狼、δ狼附近區域靠攏,這樣極易陷入局部最優,影響算法的收斂速度。該文采用的位置更新公式采用不同的權重參考三類頭狼的位置信息,對級別越高的狼參考權重相應越大,以加快收斂速度;并加入了隨機擾動以防止陷入局部最優解,其公式表達如下:

(17)

3.4 改進灰狼算法流程

改進灰狼算法流程如圖2所示。

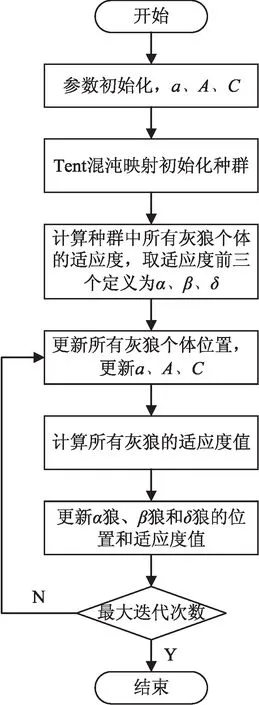
圖2 改進灰狼算法流程

4 仿真實驗及分析

4.1 實驗參數設置

實驗仿真軟件為Matlab R2018b。參照元啟發式算法比較文獻[21]和各算法的參考文獻中對實驗參數的設置,結合實際實驗過程中算法的性能和收斂效果,對各個算法的參數設置如下:GWO和ITAGWO的種群大小為100;CSA的種群大小為100,鳥蛋被發現概率為0.3,步長因子α為0.015,萊維飛行中的β因子為1;PSO中粒子數量為500,個體學習因子為0.1,社會學習因子為0.075,慣性因子為1;IA的抗體種群個數為100,免疫選擇比例為20%,抗體克隆擴增倍數為5,種群刷新比例為抗體種群的30%;SA的初始溫度為1 000,終止溫度為1e-3,降溫因數為0.9,Metropolis準則鏈長為200,種群大小為100;GA的種群規模為100,交叉概率為0.7,變異概率為0.001;TLBO的種群大小為100。查閱群智能算法相關文獻發現,其迭代次數一般設置為100～500,結合實驗迭代終止時次數均在50以內的情況,考慮到未來更復雜區域和更龐大數量充電樁的場景,該文所有算法的終止迭代次數均為300次,種群搜索維度為10。

假設空間中存在一個100 km*100 km的正方形區域,坐標范圍為(0,0)到(100,100),將空間劃分成四個子區域,每個子區域中有10個充電樁,以區域中充電樁全部連接時總線路長度最小為目標進行實例仿真,各區域充電樁的坐標見表1。

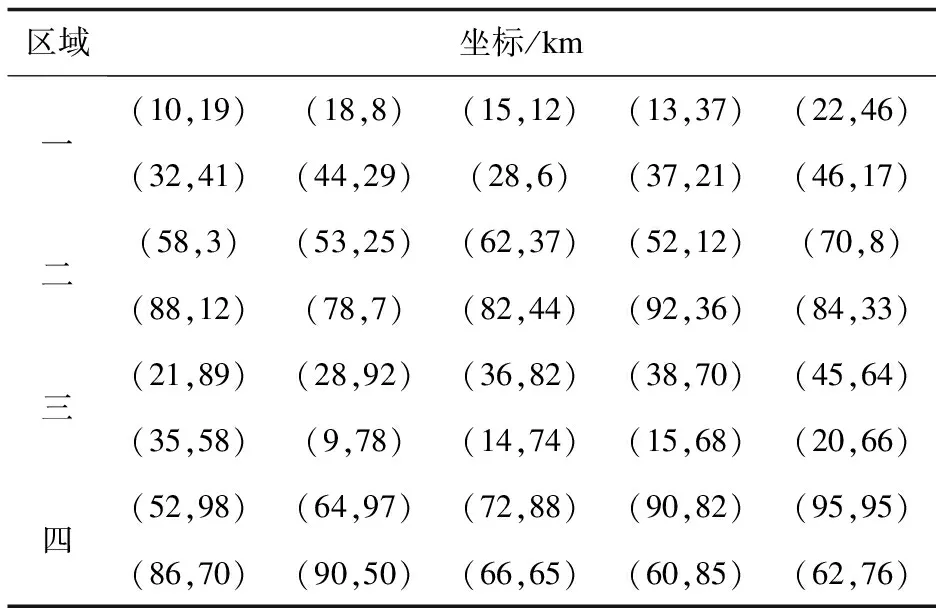
表1 各區域充電樁坐標

區域中所有充電樁的坐標位置分布情況見圖3。

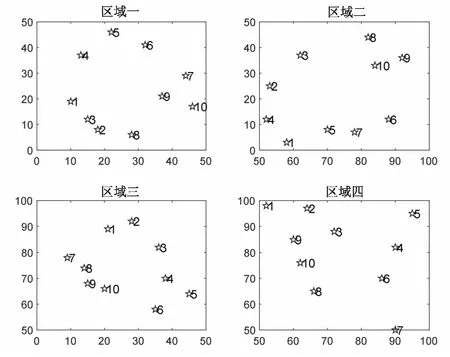
圖3 區域充電樁位置分布

4.2 算法對比分析

利用ITAGWO和七種比較算法對表1中的充電樁仿真五次,雖然各種算法求得最優解的迭代次數不同,但其所求的最優解是相同的,且其最優供電線路也一致。各算法五次仿真的平均迭代次數和最優迭代次數見表2,最優供電線路規劃方案見圖4。

表2 各算法在四區域的迭代次數

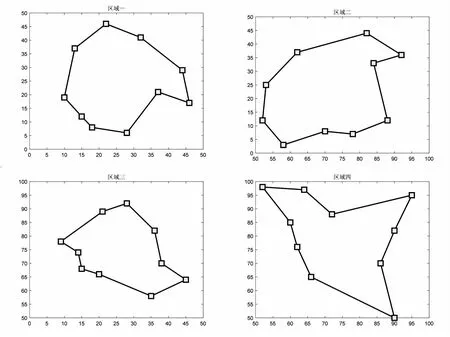
圖4 各區域能源調度路線規劃

由表2,ITAGWO與其他七種比較智能算法都可以找到最優解,但ITAGWO的迭代次數更少,收斂速度更快,且迭代次數間方差較小,更具穩定性。

在區域一,各比較算法中GWO的平均迭代次數和最優迭代次數均最少,ITAGWO的平均迭代次數和最優迭代次數分別比GWO提高了31.6%和40%;在區域二,各比較算法中GWO的平均迭代次數和最優迭代次數均最少,ITAGWO的最優迭代次數雖然與GWO一致,但平均迭代次數提高了25.8%;在區域三,各比較算法中IA的平均迭代次數最少,GWO的最優迭代次數最少,ITAGWO的平均迭代次數比IA提高了18.5%,最優迭代次數比GWO提高25%;在區域四,各比較算法中GWO的平均迭代次數和最優迭代次數均最少,ITAGWO的平均迭代次數和最優迭代次數分別比GWO提高了39.5%和33.4%。

5 結束語

針對城市中電動汽車充電樁分布的隨機性和不均勻性,將灰狼算法用于其供電線路規劃。GWO算法存在易陷入局部最優解、初始種群分布不均勻和后期收斂速度慢等缺點,該文提出一種基于Tent混沌映射和自適應收斂因子的ITAGWO算法。實例仿真結果表明,在到達最優解的前提下,ITAGWO比其余七種算法的迭代次數少、收斂速度快且穩定性好,可以很好地應用于充電樁供電線路規劃。