基于信息熵更新權重的數據自適應聚類研究

張福華，劉麗，朱俊東，朱再新，余大權

（安徽明生恒卓科技有限公司，安徽 合肥 230000）

近年來，信息技術不斷發展，互聯網信息技術、工業信息技術、通信信息技術等行業迅速崛起，這些行業產生了大量的數據。在當前階段，主要是通過自適應聚類對數據進行整合。數據通常以靜態的形式存放在數據庫中，以便隨時提取。但由于信息產生方式、性質以及數據庫的存儲量是有限的，數據的存放只能是短暫性的，并不能長期存放在數據庫中，而在應對大量的數據產生時，數據庫無法永久保存所有數據，因此數據的自適應聚類便成為解決該問題的方式。

為了解決上述問題，一些學者進行了數據自適應聚類相關研究。文獻[1]提出了基于信息熵加權的空間聚類算法，通過引入信息熵權重約束模式，完成對數據的自適應聚類，但此方式只適用于少量信息的多次自適應聚類，在應對大量數據時仍無法很好地進行聚類，導致聚類準確性變差。文獻[2]提出了基于信息流加權的集成分類算法，通過引入集成分類算法賦予數據更高的權重，并根據每個數據類別特征構建分類器，以此完成數據的自適應聚類，但此方式對于大量雜亂的數據無法做到精準聚類，實際應用效果并不好。

針對目前聚類方法的漂移點篩選能力和抗干擾能力較弱的問題，設計了一種基于信息熵更新權重的數據自適應聚類方法，并通過實驗對該方法的有效性進行了驗證。

1 基于信息熵的數據屬性加權

利用信息熵的加權對混亂數據進行自適應聚類，在構建信息熵的加權機制前，設計一種混亂數據相異性度量方式[3-4]。

由于所研究的數據為混亂數據，因此采用K-P算法統計當前數據集中相似數據出現的頻率，并設定模糊類中心，以此能夠更加直觀地度量數據之間的相異性。

根據信息熵權重建立模糊類中心，計算公式如式（1）所示：

其中，xi表示第i個數據集；C表示數據集數據的所屬類別。

而數據集中的單一對象也可表示為模糊類中心的形式，該式為模糊類中心一種特殊的表示形式[5-6]。

信息熵具有兩種形式，分別為數值型與分類型，針對數值型的數據屬性進行加權時，需應用到二階Renyi 熵，Renyi 熵具有良好的計算特性[7-8]。假設X是由獨立分布的N個數據對象組成的數據集合，計算熵值f(X)如式（2）所示：

其中，Wi為parzen 窗口函數，通常為高斯核函數。通過parzen 窗口估計法得到的熵通常為正數，上述定義給出的類內熵值反映了在聚類分化結果中某一類的值在不同屬性數據情況下的分布狀態，即一個類的類內熵越小，聚類過程的數據屬性權重越大[9-10]。

互補信息熵計算公式如式（3）所示：

根據以上分析可知，通過信息匹配得到數據熵，在完成數據聚類之后確定信息的不同屬性，根據不同屬性實現數據分離，從而實現數據屬性加權。

2 基于信息熵更新權重的數據自適應聚類

在完成基于信息熵的數據屬性加權后，對數據進行自適應聚類，聚類流程如圖1 所示。

圖1 基于信息熵更新權重的數據自適應聚類流程

根據圖1 可知，聚類過程首先構建一個數據自適應聚類器，然后完成聚類模型更新，同時進行基礎聚類器更新和權重更新實現數據自適應聚類。

構造一個數據自適應聚類器流程，假設E為一個由k個基礎聚類器y組成的自適應聚類器，設S表示數據總量，將S平均分成大小相等的數據塊B，此時自適應聚類器開始初始化，當一個新的數據塊到達時。若數據塊中的所有數據都能夠被識別，則可將該數據塊轉變為一個基礎聚類器，當基礎聚類器的個數未達到閾值k時，將不斷轉化可識別的數據塊為基礎聚類器，直到基礎聚類器的數量達到k個[11-12]。自適應聚類器由多個基礎聚類器組成，若要建立一個性能完好的自適應聚類器，則需要保證基礎聚類器具有多樣性與準確性。滿足基礎聚類器的多樣性條件是數據塊都建立在不同維度的子空間中，因此每個數據塊的維度與空間特征都是隨機的。

為了解決數據不穩定的問題，需要使用IEWU算法對自適應聚類器進行更新，更新分為基礎聚類器的更新以及基礎聚類器權重的更新兩部分。

由于IEWU 算法的中心思想與自適應聚類器的構建過程相似，因此在相似數據的數量達到一定程度時便可組建一個數據塊，通過數據塊得到一個基礎聚類器。基礎聚類器的權重隨著數據塊屬性與性能的變化而變化，以此解決數據不穩定問題。數據塊的大小決定了基礎聚類器的性能。較大的數據塊可以組建成性能更好的基礎聚類器，分類性能更佳。因此在基礎聚類器更新過程中，需要篩選出較大的數據塊來提升基礎聚類器的性能[13-14]。

由于使用IEWU 算法構建了一個混合類型的自適應聚類器，因此在IEWU 算法應用過程中，需要不利用新的基礎聚類器來替換舊的基礎聚類器，并需要對已有的基礎聚類器進行學習，結合信息熵對每個基礎聚類器的權重進行更新。通過此方式可以篩選出性能更好的基礎聚類器，提高整個自適應聚類器在面對不穩定數據時的處理能力[15]。信息熵為此次研究的重要參數，利用IEWU 算法計算信息熵的計算公式如下：

式中，H表示信息熵；P表示聚類器參數。采用IEWU 算法可求得當前數據屬性的信息熵值，由于信息熵能夠表示聚類結果的不確定性，因此信息熵越大，聚類結果的不確定性越強。當利用IEWU算法所求得的信息熵足夠小時，即可判定當前聚類結果準確。由于不同數據的信息熵都不相同，因此采用動態自適應的方式對信息熵進行更新，信息熵更新閾值計算公式如下：

式中，em為信息熵更新閾值；et為信息熵的平均值；en為信息熵的最小值，et與en的值會隨著數據屬性的不斷變化而發生改變。當IEWU 算法所求得的信息熵值小于em時，則信息熵更新停止。

通常基礎聚類器剛建立時會被賦予最高的權重值，隨著更多數據塊的到來，每個基礎聚類器會根據信息熵的閾值判斷自身是否處于性能較好的基礎聚類器，并實時調整自身權重，使得性能較好的基礎聚類器能夠被識別出，不斷淘汰性能較差的基礎聚類器[16]。

自適應聚類器的聚類結果由所有列舉出的聚類器進行加權投票，其中IEWU 算法還使用了拋棄策略，由于基礎聚類器的性能有好壞之分，性能較差的基礎聚類器由于其不穩定性，參與投票后更容易導致聚類結果更加不準確，因此參與投票的基礎聚類器都是性能較優的。給予一個固定的權重閾值，該算法只將性能在權重閾值以上的基礎聚類器加入投票的排列之中，以此實現數據的自適應聚類[17]。

3 實驗研究

為了驗證所提出的基于信息熵更新權重的數據自適應聚類方法的實際應用效果，進行了相關實驗測試。在實驗過程中，選用此次研究的自適應聚類方法和傳統的基于人工合成的自適應聚類方法、基于數據分析的數據自適應聚類方法進行實驗對比。

為了更好地保證實驗效果，同時選用RanTree、SEAg、poker 三個不同的數據塊進行實驗對比，探究不同數據塊下的聚類準確性。得到的實驗結果如圖2-圖4 所示。

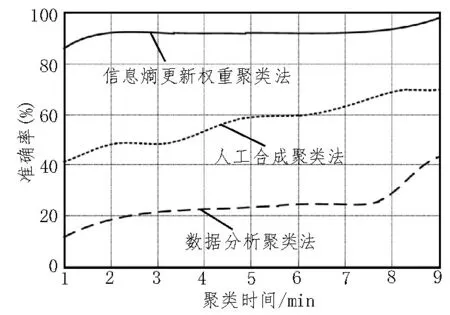
圖2 RanTree數據塊下聚類準確率

根據圖2 可知，由于RanTree 數據塊的信息環境極其不穩定，因此三種聚類方法的聚類準確率存在明顯差異。對于RanTree 數據塊，與實驗對比方法相比較，所提出的聚類方法始終保持著較高的聚類準確性。此次提出的聚類方法通過引入信息熵進行數據聚類，在不平穩的環境下也能夠很好地適應外界變化，而傳統的聚類方法在聚類過程中，容易受到外界因素影響，在不穩定的環境下可能出現準確率上升或下降的問題，難以完成快速適應，甚至會出現數據漂移，導致聚類準確率下降。

與RanTree 數據塊相比，SEAg 數據塊更加穩定，通過分析圖3 可以發現，三種聚類方法的準確率都相對較高，但是在遇見漂移點時，三種聚類方法的準確率都有所下降，此次提出的聚類方法聚類準確率僅有2%～5%的下降，而傳統的基于人工合成的自適應聚類方法準確率下降超過20%，基于數據分析的數據自適應聚類方法準確率下降超過50%，由此可見，所提出的聚類方法抗干擾能力更強。

圖3 SEAg數據塊下聚類準確率

根據圖4 可知，poker 數據塊存在的漂移點極少，但是聚類過程容易受到外界干擾因素影響，因此三種聚類方法在前期的聚類準確率都相對較低，但是隨著聚類時間的增加，此次所提出的聚類方法通過信息熵更新權重消除外界干擾，聚類準確率大大增加，而傳統方法依舊難以滿足精準聚類要求，導致聚類質量下降。

圖4 poker數據塊下聚類準確率

在上述基礎上，為了進一步驗證三種方法的聚類性能，比較了三種方法的數據聚類時間，比較結果如表1 所示。

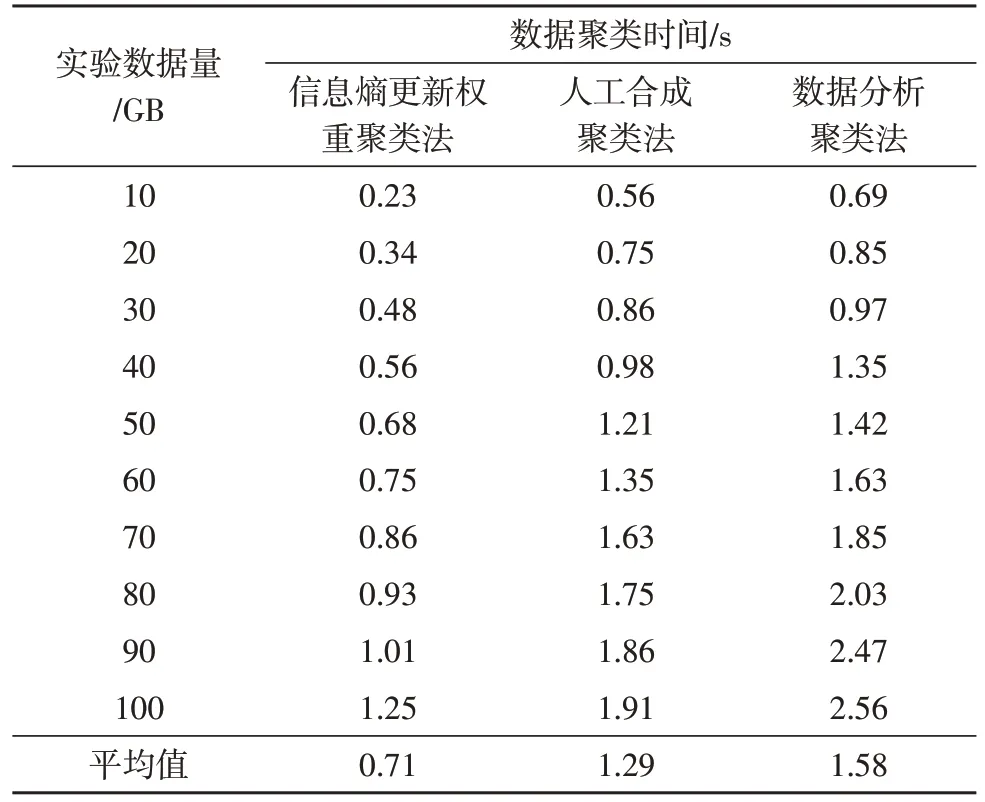
表1 數據聚類時間比較

分析表1 中的數據可知，隨著實驗數據量的增加，不同方法的數據聚類耗時均呈現上升趨勢，當實驗數據量達到100 GB 的情況下，三種方法的聚類時間均達到最大值。其中信息熵更新權重聚類法的聚類時間最大值為1.25 s，平均值為0.71 s；人工合成聚類法的聚類時間最大值為1.91 s，平均值為1.29 s；數據分析聚類法的聚類時間最大值為2.56 s，平均值為1.58 s；基于信息熵更新權重的數據自適應聚類方法的聚類時間更短，效率更高。

4 結束語

該文以解決當前聚類方法的漂移點篩選能力和抗干擾能力較弱的問題作為研究目標，設計了一種基于信息熵更新權重的數據自適應聚類方法。通過混亂數據相異性度量完成數據屬性加權，構建基礎聚類器，利用多個基礎聚類器構建自適應聚類器，以此達到自適應聚類數據的最終目標。實驗表明，此次提出的基于信息熵更新權重的自適應聚類方法解決了當前方法中存在的問題，能夠在數據自適應聚類領域得到廣泛應用，以此提升數據的聚類質量。