基于IBAS-BP算法的鋼筋混凝土中鋼筋腐蝕程度預測模型
黃 雷,俞阿龍
(1.南京工業大學電氣工程與控制科學學院,南京 211800;2.淮陰師范學院物理與電子電氣工程學院,淮安 223300)
工程調查表明,一般情況下鋼筋混凝土結構的使用年限約為50~100 a,然而很多鋼筋混凝土結構在使用20 a左右便提前進入老化期[1],其主要原因是混凝土中的鋼筋發生腐蝕。因此,設計一種綜合多種混凝土結構內部環境和鋼筋腐蝕影響因素的鋼筋腐蝕預測模型具有重要意義。
鋼筋腐蝕程度是衡量鋼筋混凝土結構服役情況的重要參數,鋼筋腐蝕檢測技術一直受到國內外學者的廣泛關注。WU等[2]基于Texas大學提出的將鋼筋等效物與射頻技術相結合的方案,設計了一種無源腐蝕檢測傳感器,開發了相應的腐蝕監測系統,并在江蘇省連云港徐圩港區的一期工程中得到應用。張冉[3]在傳統光纖光柵高溫(FBG)傳感器監測的基礎上,提出了一種適用于全壽命期鋼筋銹蝕監測的光柵傳感器,實現了單一應變變量的測量,最后通過回歸分析方法建立了鋼筋腐蝕程度預測模型,消除了溫度對傳統光柵傳感器的影響,提高了預測準確度。XU等[4]利用超聲波對混凝土中的鋼筋棱柱進行檢測,并采用人工神經網絡模型,選取混凝土強度、超聲波速等相關變量作為輸入層,對混凝土中鋼筋腐蝕程度進行預測,具有較高的預測精度。近年來,通過智能算法來初始化BP神經網絡的權值和閾值,以達到更好的精度是目前研究的主流方向,該方法具有較好的非線性能力,同時也可避免BP神經網絡的過度擬合。任舒蕊等[5]利用天牛須搜索(BAS)算法與BP神經網絡相結合的算法(以下簡稱BAS-BP算法)來估算電池SOC,克服了BP神經網絡收斂速率慢、穩定性差等缺點,提高了估算的準確度。
由于BAS算法中初始方向隨機性強和步長自衰減的限制,初始參數設置對優化結果影響較大,為了減少初始參數的影響,避免陷入局部極小值,本工作提出改進的BAS-BP算法(以下簡稱IBAS-BP算法),將BAS算法中尋優的單只天牛改為天牛群,并對步長和自衰減系數進行設置,將改進的算法用于鋼筋混凝土中鋼筋腐蝕程度的預測,選取溫度、濕度、CO2含量、pH、氯離子含量和腐蝕電位6個鋼筋腐蝕特征量與腐蝕程度的對應關系作為預測模型的訓練樣本,建立鋼筋混凝土中鋼筋腐蝕程度的預測模型,通過試驗證明算法的有效性和優越性。
1 混凝土中鋼筋腐蝕機理及鋼筋腐蝕特征量
1.1 混凝土中鋼筋腐蝕機理
混凝土是由水泥凈漿、骨料、空氣、水等物質組成的復合材料,其孔隙液實際上是氫氧化物的飽和溶液,pH可達12~14。在這種高堿性的環境中,混凝土中的鋼筋會與水和氧氣發生反應,形成一層大約只有1 μm的鈍化膜,其較好的致密性可以隔絕空氣、水與鋼筋表面接觸,保障鋼筋不會發生腐蝕。但是,當外界環境pH<11.5時,鈍化膜的生成就變得困難,當pH<9.8時,鈍化膜幾乎完全破壞。此時,鋼筋會發生局部腐蝕,鋼筋表面可劃分為鈍化區和腐蝕區兩部分,由于這兩部分存在電位差,形成了鋼筋大陰極-小陽極的宏電池,加快了鋼筋的腐蝕速率。所以,鋼筋開始發生腐蝕的必要條件是表面鈍化膜被破壞,而造成鈍化膜破壞的因素較多,其中碳化和氯化物侵蝕是最主要的兩個因素。
1.1.1 碳化作用
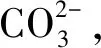

(1)
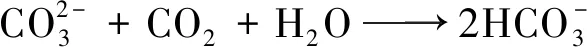
(2)
1.1.2 氯化物侵蝕
氯化物對混凝土中鋼筋腐蝕的作用往往比碳化更加明顯。氯離子半徑較小,大約為1.81 pm,具有較強的穿透性,容易穿透鈍化膜并吸附在鋼筋表面。由于氯離子活性較大,當其接觸到鈍化膜受損的鋼筋表面時,可與鋼筋直接發生反應,形成小陽極-大陰極的腐蝕電池,陽極為鋼筋受到氯離子侵蝕的部位,陰極為鋼筋表面鈍化膜尚未被破壞的部位,這種現象稱為坑蝕現象。同時氯離子還具有局部酸化的性質,當他吸附于局部鈍化膜處時,可使該處的pH迅速降低到4以下,從而使得鈍化膜溶解、破壞。氯化物侵蝕原理如圖1所示。
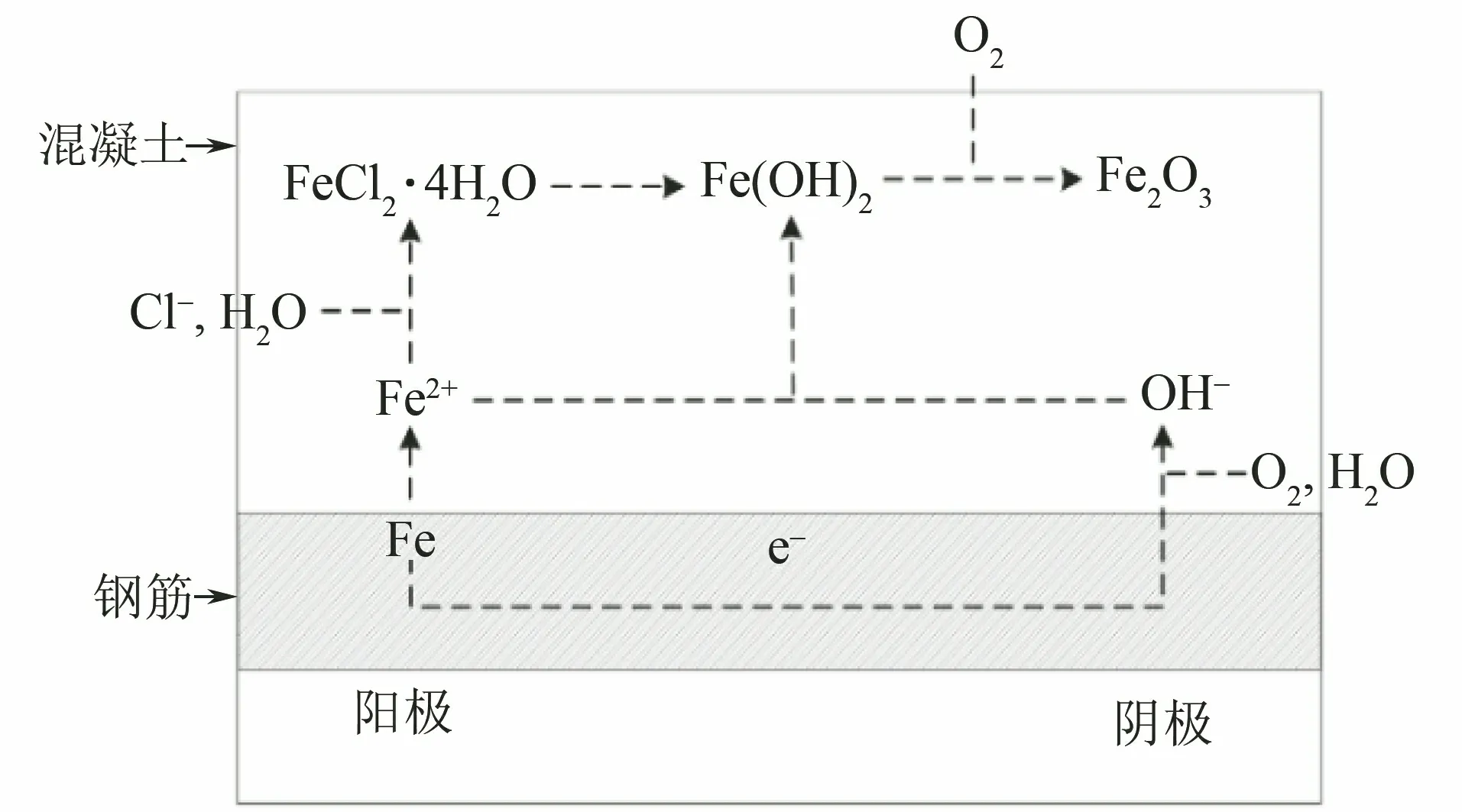
圖1 氯化物侵蝕原理示意圖
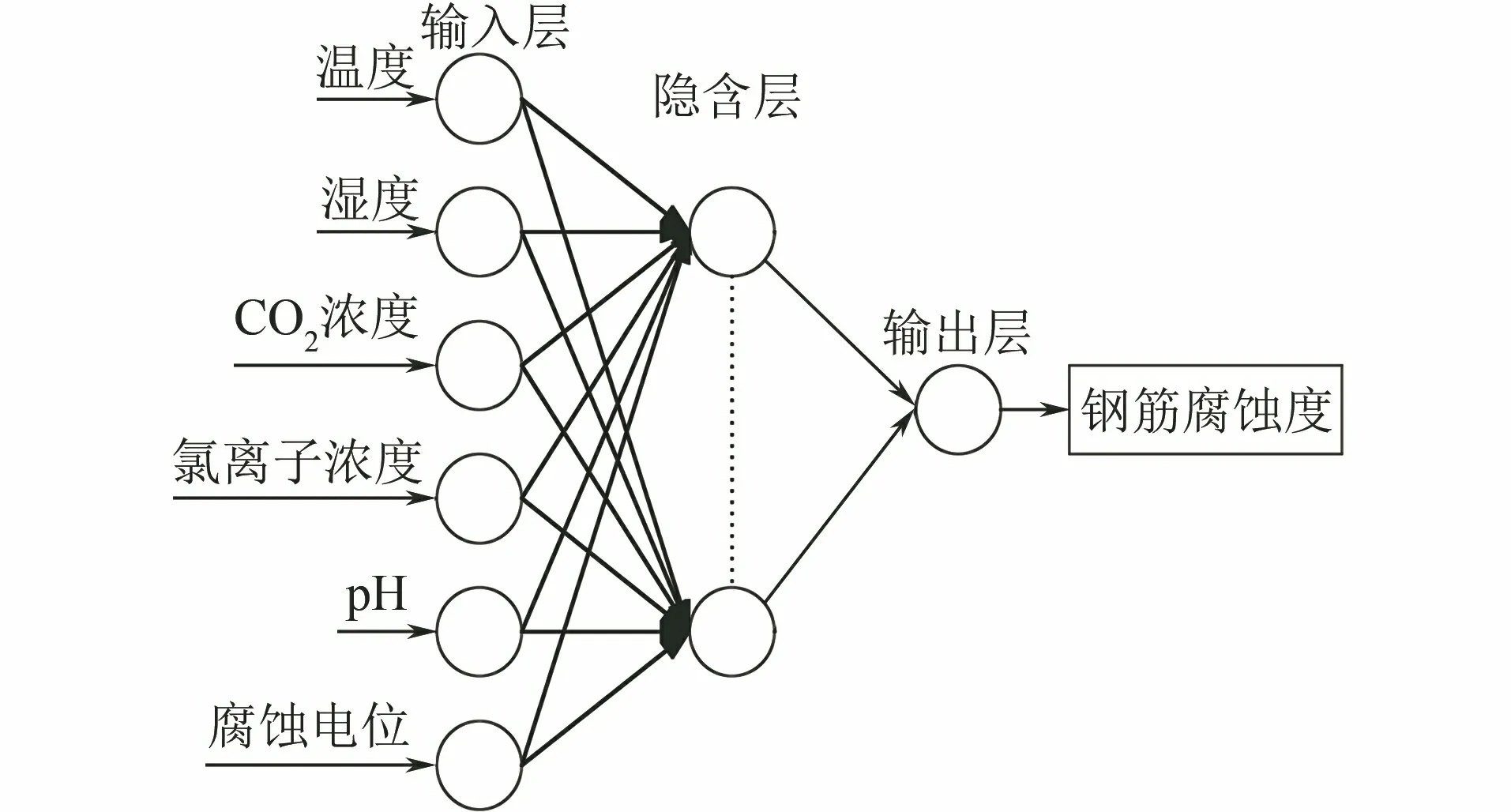
圖2 IBAS-BP預測模型
1.2 鋼筋腐蝕特征量
由混凝土中鋼筋的腐蝕機理可知,碳化和氯離子侵蝕是鋼筋腐蝕最主要的兩個因素,而這兩個因素均會降低鋼筋周圍環境的pH,使鋼筋表面鈍化膜遭到破壞,且混凝土內部的濕度也會影響碳化速率。因此選取溫度、濕度、CO2含量、pH、氯離子含量和腐蝕電位6個指標作為鋼筋腐蝕特征量。
2 IBAS-BP算法
2.1 BP神經網絡
BP神經網絡模型可以看作是基于復雜多樣的因素預測某一變量的黑箱模型。BP神經網絡是由輸入層、隱含層和輸出層組成。他是一種采用誤差反向傳播算法訓練的多層前饋神經網絡,采用梯度下降方式優化BP神經網絡的權值和閾值[7],可以提高估算的準確度,但BP神經網絡具有迭代速率慢、過度擬合和易陷入局部最優等缺點,而通過智能算法優化BP神經網絡可以有效地避免這些缺點。
2.2 標準BAS算法
BAS算法是SONG[8]提出的一種發展起來的元啟發式優化算法,該算法源于自然界天牛的隨機行走。受天牛的生物學行為啟發,BAS算法通過模擬天牛的兩條長須在相鄰的田野中尋找氣味來實現優化過程。具體來說,當長須檢測到一側的氣味濃度高于另一側時,天牛就會向一側移動,否則就會轉向另一側。由于BAS算法尋優過程的簡單性和有效性,對于單目標函數尋優速率更為快速[9],算法步驟如下。
(1) 由于天牛頭部的方向是任意的,所以從天牛的右天線到左天線的矢量方向須是任意的。標準化隨機向量b見式(3)。
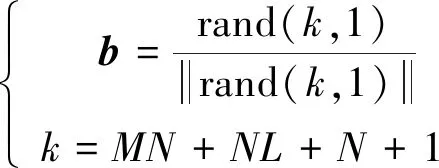
(3)
式中:rand(·)為隨機函數;k為搜索維數;M、N、L分別為輸入層、隱含層和輸出層的神經元個數。
(2) 天牛下一步的位置xt+1見式(4)。
xt+1=xt-δtbsing[f(xr)-f(xl)]
(4)
式中:xt為t次迭代后天牛所在的位置;δt為天牛在第t次迭代后的步長;b為;sing(·)為符號函數;f(xr)和f(xl)為天牛右須和左須的適應度函數。
(3) 天牛左右須空間坐標更新見式(5)。
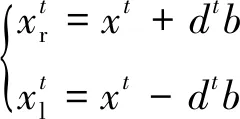
(5)
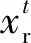
(4) 感知長度和步長的更新。為了使天牛在搜索過程更加精確,采用步長δ和感知長度d是一個由大到小的過程,如式(6)所示。
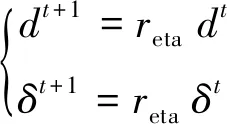
(6)
式中:reta為自衰減系數,幅值為(0,1)。
(5) 最優解生成。在迭代過程中,每次迭代后的天牛位置更新后放入xbest集中,計算出左右須的適應度函數并進行比較,然后放入fbest集中。迭代完成后,對xbest集和fbest集進行比較,得到最優解fbest和與之對應的xbest,并放入Fbest和Xbest中。Xbest就是BAS算法搜索到的最優解。
2.3 BAS算法改進
由于BAS算法中初始方向隨機性強和步長自衰減的限制,初始參數設置對優化結果影響較大,為了減小初始參數的影響,避免陷入局部極小值,提高預測模型的精確度,對BAS算法做出如下改進。
(1) 搜索單位的改進。將原先算法尋優的單只天牛改進為天牛種群,可以有效減小初始參數對試驗結果的影響,避免陷入局部極小值,在迭代過程中天牛群各只天牛位置如式(7)所示。
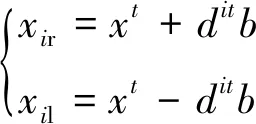
(7)
式中:xir和xil是天牛群中第i只天牛經過t次迭代后右天線和左天線的位置;dit為天牛天線的感知長度,感知長度應足夠大,以覆蓋適當的搜索區域,然后隨著時間的推移逐漸衰減。
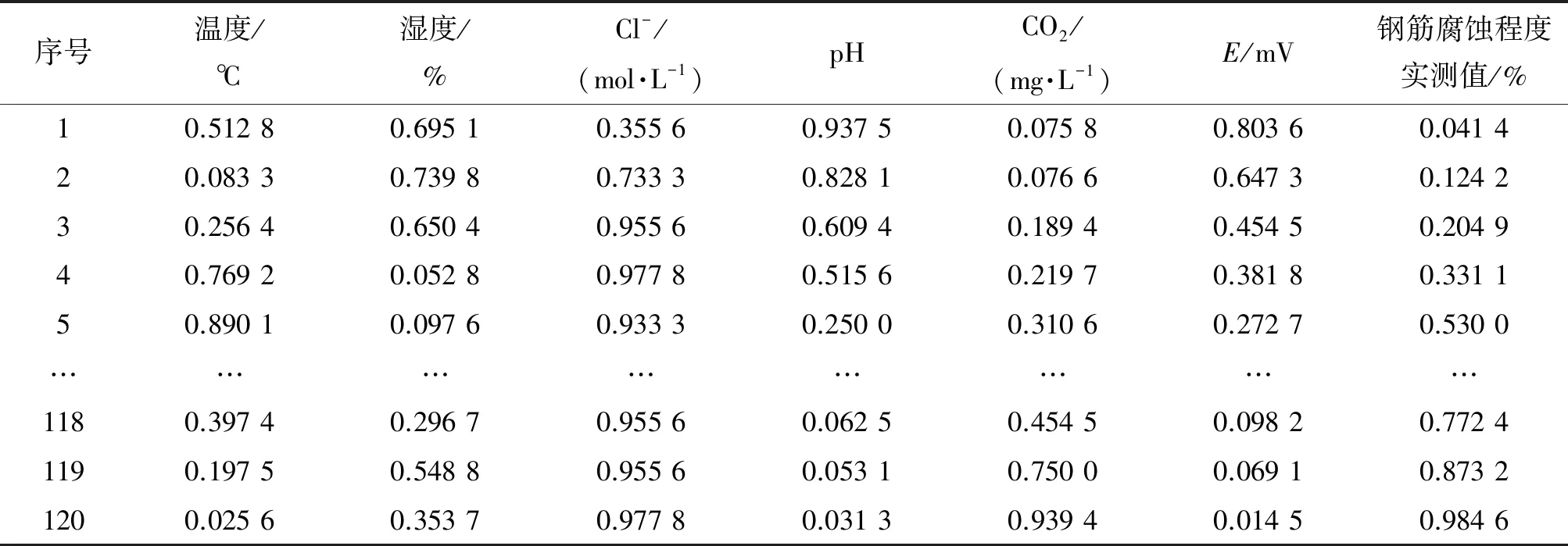
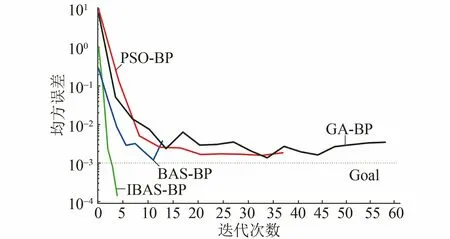
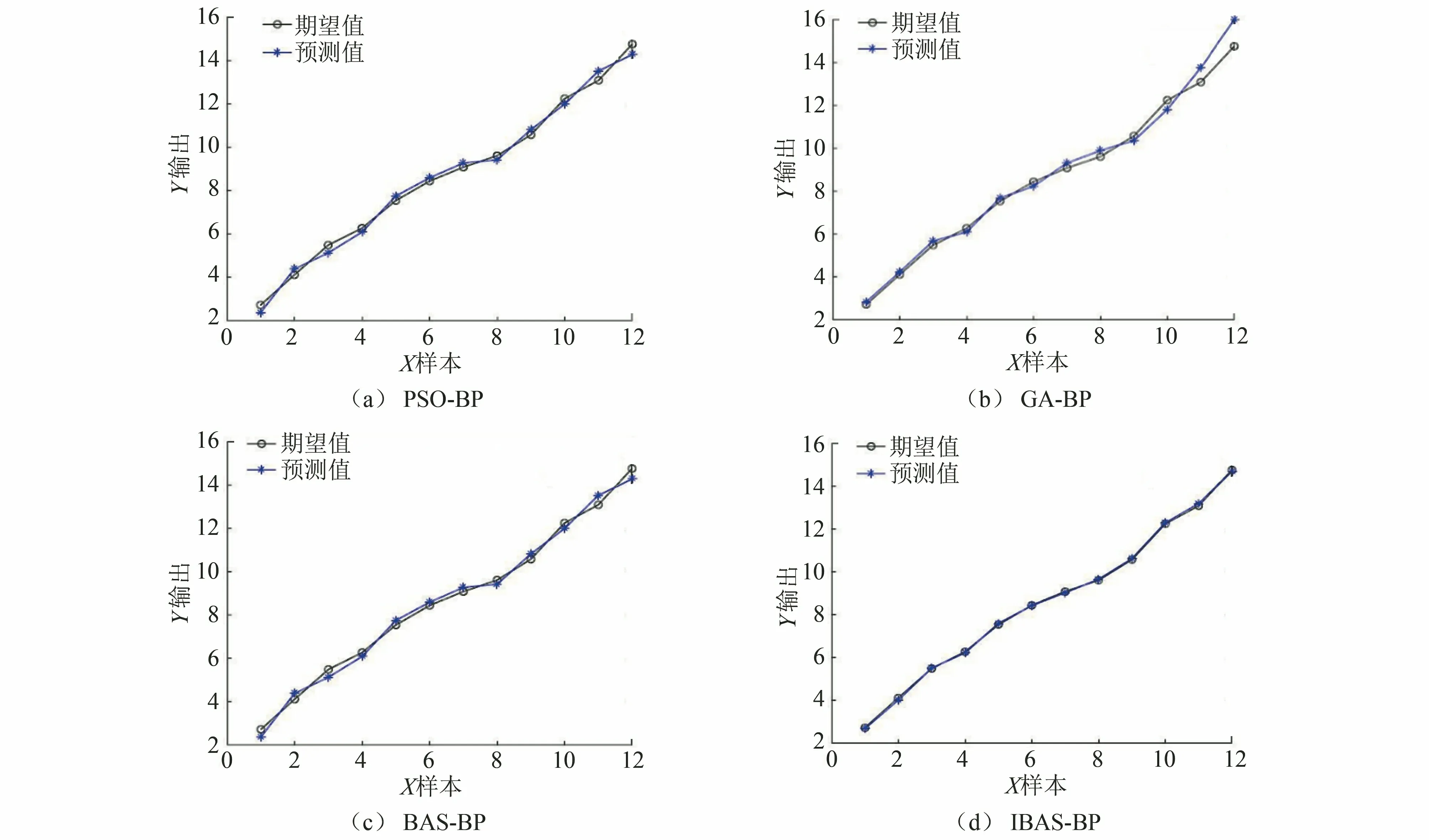
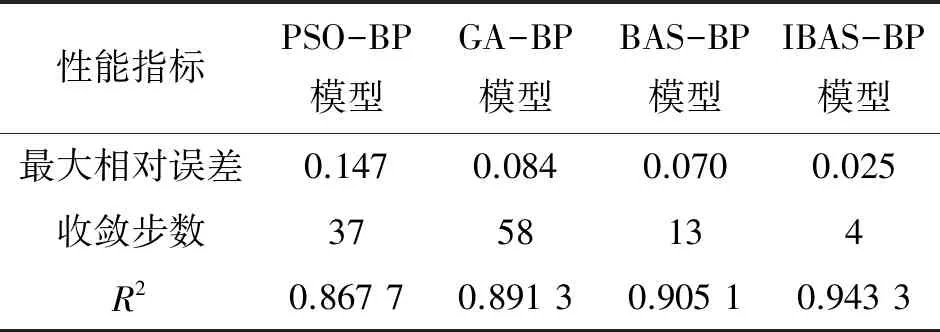
(2) 步長和自衰減系數的改進。在BAS 算法中[10],初始步長獲得最優的搜索范圍,并可以使算法的漸進收斂概率為1。所以,通過設置步長δ和自衰減系數reta兩個參數,提高IBAS算法的迭代速率。為進一步提高IBAS-BP算法的預測精度,對不同的步長和自衰減系數進行仿真。將[2,8]范圍內的步長δ依次代入并進行訓練。由訓練結果可知,當步長取4時,此時模型的迭代速率最快。將[0.55,0.99]范圍內的自衰減系數reta依次代入并進行訓練。由訓練結果可知,當0.55 選用6個鋼筋腐蝕特征量作為輸入層,輸出層為鋼筋腐蝕程度。在鋼筋混凝土內部環境因素與鋼筋腐蝕程度映射關系不明的情況下,可通過選取鋼筋腐蝕特征量的數據,實現對鋼筋混凝土中鋼筋腐蝕程度的預測。本工作中預測模型選取6個輸入節點以及一個輸出節點,由BP神經網絡隱含層的經驗公式(8)可得隱含層個數。 (8) 式中:M、m、n分別為隱含節點數、輸入層節點數和輸出層節點數;a為[1,10]范圍的正整數。由式(8)可得最佳隱含層個數的范圍為[4,13]。 將取值范圍內的隱含層個數依次代入BP 神經網絡,通過對比不同隱含層個數訓練集的均方誤差確定隱含層個數。結果表明,當本工作中預測模型的隱含層個數為8時,訓練集均方誤差最小。 IBAS-BP算法的具體步驟如下,其流程圖如圖3所示。 圖3 IBAS-BP算法流程圖 (1) 對實測選取的6個鋼筋腐蝕特征量和與之對應的鋼筋腐蝕程度的數據進行歸一化。 (2) 初始化天牛群參數,天牛群中各只天牛的初始位置都應設置在 [-0.5,0.5]范圍內的k維隨機向量,設置感知長度d為30,步長δ為4,自衰減系數reta為0.95,最大迭代次數為200,設定適應度函數值為0.001。 (3) 確定適應度函數對天牛左右須進行氣味判斷,通過式(9)得出最優解Xbest。 (9) 式中:tsim(j)和yj分別為第j個樣本的預測值和真實值。 (4) 根據式(3)和式(5)~(7)更新天牛群中各只天牛位置以及各天牛左右須位置,并得到與之對應的適應度函數,當迭代次數達到預設的最大迭代數或者適應度函數值小于設定精度時,停止迭代,得到的Xbest就是利用改進后的算法求得的BP神經網絡最優的初始權值和閾值。 (5) 將IBAS算法尋優結果,即最優的BP神經網絡初始權值和閾值代入,進行二次訓練。 混凝土中鋼筋腐蝕是一個非常復雜的過程。為了能盡可能多的考慮不同工程環境和影響因素,選取了溫度、濕度、CO2含量、pH、氯離子含量和電極電位作為腐蝕影響參數,根據標準JGJ/T 98-2010《砌筑砂漿配合比設計規程》和GB/T 27690-2011《砂漿和混凝土用硅灰》,以1…2…6的水灰沙比制備混凝土測試試塊[11],在試塊澆筑并養護完成后進行電化學加速腐蝕試驗。對不同鋼筋腐蝕程度的試塊進行破壞性試驗,得到試塊中的鋼筋,并根據鋼筋酸洗堿洗前后的質量差,計算鋼筋的腐蝕程度。 對不同量級的訓練數據進行歸一化處理不僅可以消除數據本身造成的不良影響,還能加速梯度下降,找到最優解并提高算法精度。本工作通過MATLAB軟件中的歸一化函數,將數據歸一化在[0,1],歸一化后的數據如表1所示。 表1 歸一化后的訓練樣本數據 將試驗數據依次代入PSO-BP、GA-BP、BAS-BP和IBAS-BP 4種模型中,得到4種模型驗證均方誤差曲線。 由圖4可見,GA-BP模型需要58步收斂,PSO-BP模型需要37步收斂,BAS-BP模型需要13步收斂,IBAS-BP模型只需要4步就已經收斂,在收斂速率上是4種模型中最快的。測試集的試驗結果和預測結果對比如圖5和表2所示。 表2 預測結果對比 圖4 4種模型驗證均方誤差曲線 圖5 4種模型的試驗結果 為合理評價和改進 IBAS-BP 模型對于鋼筋混凝土中鋼筋腐蝕程度的預測精度,以測試樣本數據的相對誤差、收斂速率和決定系數為評估標準。決定系數R2的計算公式見式(10)。 (10) 式中:NSSR為回歸平方和;NSSE為誤差平方和;NSST為總平方和;tsim(j)和yj是第j個樣本的預測值和真實值;y為測試集樣本真實值的平均值。 R2在0到1之間,當R2越靠近1時,表明模型的擬合度越高。不同模型的性能對比結果如表3所示。 表3 不同模型的性能對比 由表2和表3可見,PSO-BP模型的預測值與實際鋼筋混凝土中鋼筋的腐蝕程度定值基本吻合,但當鋼筋腐蝕程度低于6%和高于13%時,預測結果較期望值相差較大。性能指標方面,PSO-BP模型的最大相對誤差為0.147,決定系數R2為0.867 7,在預測精度和擬合能力上是4種模型中表現最不理想的。當鋼筋腐蝕程度大于13%時,GA-BP模型預測結果的誤差變大。性能指標方面,GA-BP模型的最大相對誤差為0.084,決定系數R2為0.891 3,預測精度和擬合能力低于BAS-BP模型,并且遺傳算法步驟繁雜,收斂速率是4種模型中較慢的。BAS-BP模型的預測值與期望值的誤差相對較小,但當腐蝕程度在13%以上和在6%以下時,出現誤差。性能指標方面,BAS-BP模型的最大絕對誤差為0.070,決定系數R2為0.905 1,由于BAS算法尋優速率快,BAS-BP模型的收斂速率相對于前兩種模型較快,但初始參數設置對試驗結果影響較大。IBAS-BP模型的預測值和期望值基本吻合,誤差是4種模型中最小的,其最大相對誤差僅為0.025,決定系數R2為0.943 3,IBAS-BP模型僅需4步就能收斂,收斂速率比BAS-BP模型更快。 通過將混凝土內部溫度、濕度、CO2含量、pH、氯離子含量和腐蝕電位作為模型輸入層,鋼筋腐蝕程度作為輸出層,利用改進IBAS-BP算法建立預測模型,對混凝土內部鋼筋腐蝕程度進行預測。試驗結果表明,IBAS-BP模型對于鋼筋混凝土中鋼筋腐蝕速度的預測精度得到提高。通過調整天牛的步長和自衰減系數,預測模型不斷優化,模型預測結果的誤差也隨之減小。將試驗數據代入4種模型中進行訓練,并比較試驗結果和模型性能指標,得出 IBAS-BP模型在預測精度、收斂速率和決定系數方面的表現都優于BAS-BP模型、GA-BP模型和PSO-BP模型,表明了基于IBAS-BP算法的鋼筋混凝土中鋼筋腐蝕程度預測模型具有更好的預測效果。3 IBAS-BP算法在鋼筋腐蝕程度預測中的應用
3.1 IBAS-BP模型
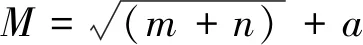


3.2 試驗數據
3.3 試驗結果

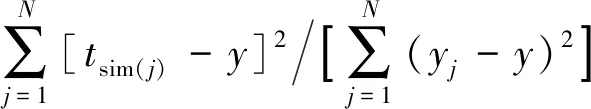
4 結 論

