基于變尺度杜芬陣列的超聲非線性輸出信號檢測

張玉華, 全四龍, 劉樹博

(東華理工大學機械與電子工程學院, 南昌 330013)

在超聲非線性檢測中,當激勵超聲波在金屬材料內部傳播時,由于材料微觀缺陷或疲勞損傷的存在,超聲波與疲勞損傷發生非線性相互作用,激勵波形發生畸變,能量發生偏移產生高次諧波,相關研究表明產生的高次諧波能與材料疲勞損傷缺陷密切相關[1-3]。超聲波在材料內部傳播過程中,由于環境噪聲和實驗設備的影響,反映材料損傷的微弱高次諧波信號湮沒在強背景噪聲下[4]。有效分析和檢測強背景噪聲下的高次諧波信號對有效評估材料的疲勞損傷是非常關鍵的。

隨著混沌理論的發展,利用混沌理論對非線性信號進行分析越來越受到關注[6]。杜芬混沌振子具有對初值條件敏感且對噪聲免疫的特點,是一種最常用的微弱周期信號檢測方法[7-8]。杜芬混沌振子對初值條件的敏感依賴性表現為周期驅動力幅值F0對系統運動狀態的影響,當杜芬振子處于混沌狀態時,一個較小的擾動信號會使系統狀態變為大尺度周期狀態,通過系統狀態的變化可以實現微弱信號的檢測[9]。

利用杜芬振子對微弱待測信號進行檢測時,需要非常嚴苛的條件才會使系統運動狀態發生變化,如待檢測信號的頻率為1、初始相位為0、待檢測信號與杜芬系統幅值匹配等條件,這嚴重限制了杜芬混沌振子對實際工程信號的檢測。如何利用杜芬振子對實際工程信號進行檢測是一個非常復雜的問題。

為了利用杜芬振子對具有任意幅值、任意頻率和任意相位的實際工程信號進行檢測,現首先利用頻率轉換方法,對杜芬振子進行改進,使杜芬振子能夠檢測任意頻率的待測信號;其次,探究待測信號和驅動力信號初始相位對檢測結果的影響,提出利用杜芬振子陣列對對信號進行檢測;為了匹配待檢測信號和杜芬振子,對待檢測信號進行變尺度變化;最后根據待測信號驅動力幅值和響應信號幅值之間的對應關系,對待測信號幅值進行估計。基于以上研究,提出對實際工程信號進行檢測的杜芬振子檢測模型,對超聲非線性輸出信號中的二次諧波信號進行檢測,并分析噪聲對檢測結果的影響。

1 構建杜芬陣列檢測模型

1.1 杜芬振子檢測原理

常規杜芬方程為

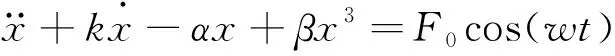
(1)

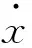
當驅動力幅值F0由0不斷增加時,杜芬振子相圖具有復雜的運動狀態,如同宿軌道F0=0.382、分叉F0=0.386、混沌F0=0.626、臨界混沌F0=0.826和大尺度周期F0=0.827等狀態。

當利用杜芬振子對微弱信號檢測時,將檢測信號S輸入杜芬振子中,即

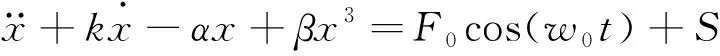
(2)

如果S與驅動力F0cos(w0t)具有相同的角頻率w0,設定驅動力幅值F0=0.826,此時杜芬振子為臨界混沌狀態;當待檢測信號S輸入杜芬系統后,通過數值變換,式(1)右側相當于增加杜芬振子的驅動力幅值F0,如果總驅動力幅值大于分叉閾值Fc=0.827,杜芬系統的相圖由混沌狀態轉換為大尺度周期狀態[10]。因此,待檢測信號S可以根據杜芬系統相圖的變化進行檢測。

利用杜芬振子對實際信號進行檢測時,需要非常嚴苛的條件才會使系統運動狀態發生變化,如待檢測信號的頻率為1、初始相位為0等條件,這嚴重限制了杜芬混沌振子對實際工程信號的檢測。

1.2 頻率轉換

在實際應用中,待檢測的頻率一般不為1,為了使用杜芬振子檢測任意頻率的實際工程信號,對杜芬振子進行頻率轉換[11-12]。

設定t=w0τ,w0為待檢測信號的頻率,引入新的位移變量x*(τ),則

(3)

而式(2)則可以改變為

F0cos(w0τ)+S

(4)

(5)

式(5)由式(2)線性轉換得到,因此兩組等式的分叉閾值Fc保持不變,即Fc=0.827。

1.3 待測信號相位對檢測結果影響

利用杜芬振子對微弱信號檢測時,設驅動力信號和待檢測信號的初始相位分別為φ和δ,其中-π<φ、δ<π。含有待測信號的杜芬系統為

[acos(t+φ)+n(t)]

(6)

式(6)中:δ為驅動力信號的初始相位;φ為待檢測信號的相位;a為待檢測信號幅值;n(t)為隨機噪聲。

令δ=0,引入新的幅值變量A(t),對式(6)右端進行簡化得

A(t)=0.826cost+acos(t+φ)

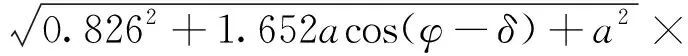
cos(t+θ)

(7)

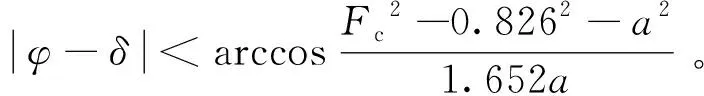
表1 杜芬振子的初始相位檢測范圍Table 1 Initial phase detection range of Duffing equation

由表1可知,當驅動力信號的初始相位δ分別為0、90°、180°和-90°時,微弱待測信號被檢測出來的初始相位檢測窗口為(-60°,60°)、(30°,150°)、(120°,240°)和(-150°,-30°),這4個窗口覆蓋-180°～180°的整個搜索空間。也就是說,當待檢測信號的初始相位φ為任意角度時,只要滿足幅值條件,4個杜芬振子構成的杜芬陣列中至少有一個滿足相位檢測條件,使杜芬振子相圖發生變化,從而實現任意初始相位的待測信號檢測。因此,可以用驅動力信號初始相位δ分別為0、90°、180°和-90°時構成的杜芬陣列對微弱信號S進行檢測。

1.4 待測信號幅值的估計

當杜芬檢測振子在大尺度周期狀態下,如果系統的總驅動力越大,杜芬振子的響應越明顯,在相軌跡圖中表現為橫坐標最大值xmax越大[14-15]。通過仿真分析發現,當杜芬振子的總驅動力由F1增加至F2時,響應幅值由E1增加至E2,這說明杜芬振子的輸入總驅動力幅值與響應幅值之間具有一一對應關系。所以,根據總驅動力幅值與響應幅值之間的對應關系可以估算待測信號的幅值。

基于以上分析,利用杜芬振子對實際的工程信號S進行檢測的杜芬陣列檢測模型為

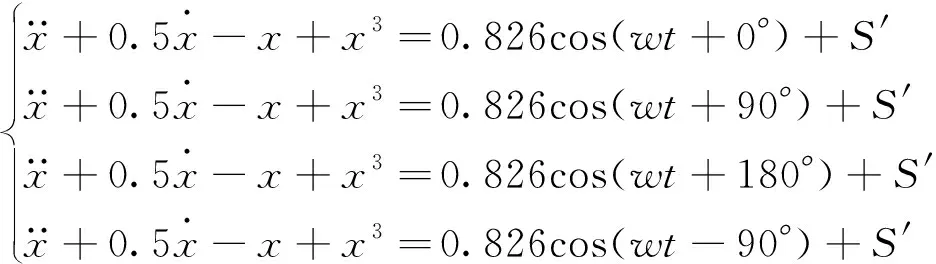
(8)

式(8)中:S′=ηS;η為變換系數;S′為待測信號S經過線性幅度變換后得到的。

當實際的工程信號作為待測信號導入杜芬檢測陣列時,待測信號的幅值要適當,幅值過大會使相圖軌跡變得雜亂無章,而幅值過小則不會對相圖產生影響。因此,為了使待測信號和杜芬振子相匹配,對待測信號S乘以變換系數η進行線性幅度變換。

當使用杜芬陣列對實際工程信號進行檢測時,具體的檢測步驟如下。

(1)對不同疲勞損傷程度的試件進行超聲非線性試驗,得到實測的超聲非線性輸出信號S。

(2)對實測的超聲非線性輸出信號進行預處理,將待測信號乘以一個合適的變換系數η,得到幅值變換后的待測信號S′。

(3)確定杜芬陣列的參數,令c=0.5、α=β=1、F0=0.826,初始值為(0,0),得到超聲非線性輸出信號的杜芬陣列檢測模型,并畫出未加入待測信號S的振子相圖。

(4)輸入待測信號到檢測模型,使用四階龍格-庫塔算法對模型進行求解,得到輸入待測信號后的杜芬陣列相圖,并與步驟(3)中的相圖進行比較,只要4個相圖中有其中一個由混沌狀態過渡至大尺度周期狀態,則待測信號S就可以被檢測出來。

(5)利用相圖改變的Duffing振子,分析待測信號幅值和響應幅值之間的關系,建立兩者之間的關系曲線,利用關系曲線對微弱待測信號的幅值進行估算。

2 金屬試件疲勞損傷狀態的檢測

2.1 二次諧波信號的檢測

在超聲非線性技術中,高次諧波技術常用來研究金屬試件的非線性。由于金屬材料的早期疲勞損傷、微裂紋和材料性能退化等,超聲波在金屬材料內部傳播時,波形發生畸變產生高次諧波,產生的高次諧波與材料的損傷狀態密切相關,可利用高次諧波對材料的損傷狀態進行表征。接收傳感器接收到的超聲非線性輸出信號包含表征材料非線性狀態的高次諧波信號,與激勵信號相比,高次諧波信號比較微弱,且湮沒在背景噪聲中。因此,利用杜芬方程的噪聲免疫和對微弱信號敏感的特性,對超聲非線性輸出信號中的二次諧波信號進行檢測[16]。

當激勵信號頻率為2.4 MHz,對疲勞壽命為40%的標準試件進行超聲非線性試驗,采集接收傳感器的超聲非線性輸出信號,信號時域波形如圖1所示。

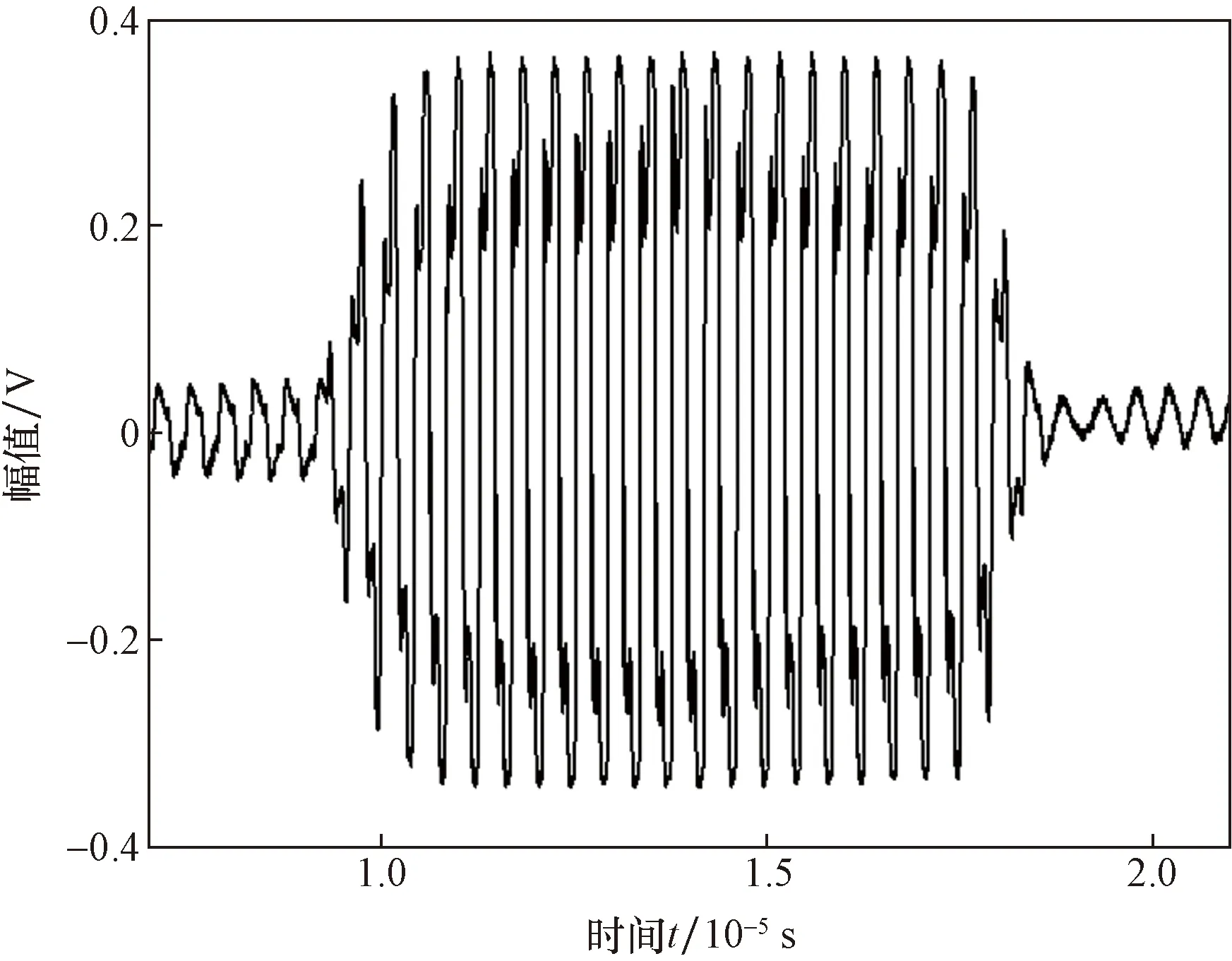
圖1 超聲非線性輸出信號的時域波形Fig.1 The time-domain waveform of ultrasonic nonlinear signal

由圖1可知,由于試件已經發生疲勞損傷,頻率為2.4 MHz的超聲波發生畸變,產生二次諧波,即頻率為4.8 MHz的信號。研究表明4.8 MHz處的二次諧波與試件的疲勞損傷程度密切相關。當使用杜芬方程對二次諧波信號進行檢測時,待檢測信號頻率w0=2π×4.8=30.16 rad/μs,杜芬陣列模型為

(9)

當待測信號S輸入杜芬陣列模型前,需要對超聲非線性輸出信號進行變尺度變換。經過仿真分析,變換系數η=0.2。將超聲非線性接收信號乘以0.2得到待檢測信號S′。將S′輸入杜芬陣列模型,使用四階龍格-庫塔算法求解等式(6),求解過程中設定計算步長h=0.004 μs,初始值為(0,0)。則對應的杜芬陣列相圖如圖2所示 。

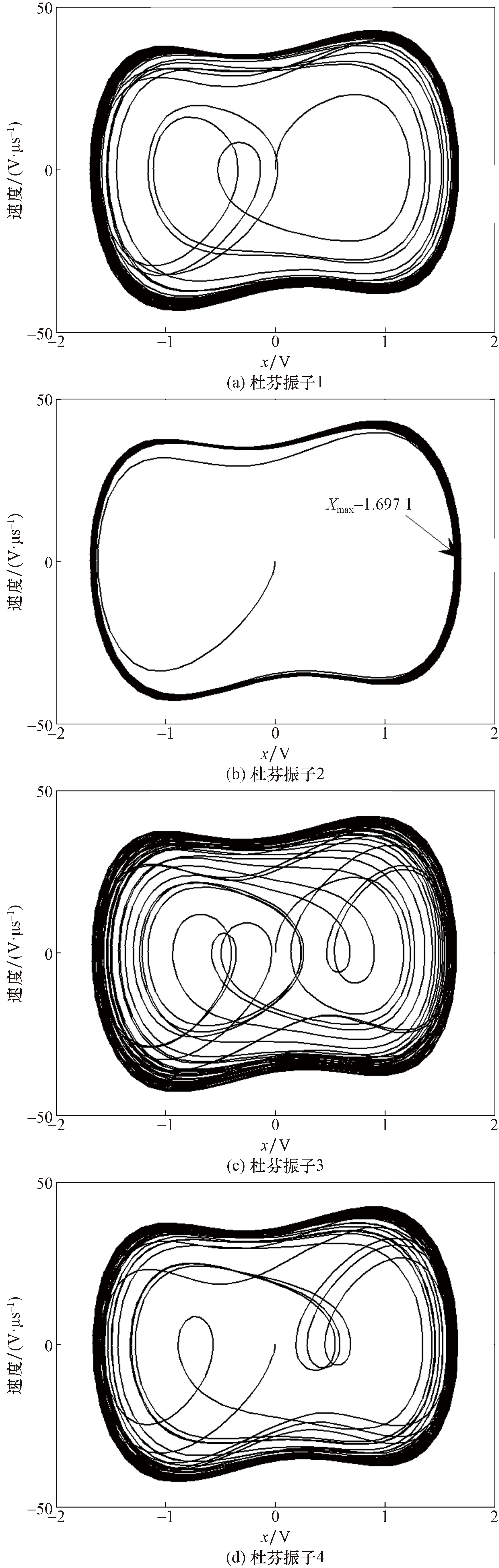
圖2 檢測二次諧波信號的杜芬陣列相圖Fig.2 Duffing array of second harmonic signal

由圖2可知,當待檢測信號S′輸入杜芬陣列后,第2個杜芬陣子的相軌跡由混沌狀態變化為大尺度周期狀態,另外3個均保持在混沌狀態。杜芬相圖的變化,說明待檢測信號中含有4.8 MHz的微弱信號,即超聲非線性輸出信號中的二次諧波信號能夠被檢測出來。從圖2(b)可知,xmax=1.679 1。

當杜芬振子的總驅動力幅值F由0.830增加至1.025的過程中,得到一系列響應幅值E,如圖3所示。

圖3 驅動力F和響應幅值E的關系Fig.3 The relation between driving force F and response amplitude E

基于圖3的試驗數據,利用最小二乘法對曲線進行擬合,得到二階最優擬合曲線為

F=3.267A2-10.3A+8.899

(10)

在圖3(b)中,相圖最大橫坐標xmax=1.697 1,即響應幅值A=1.697 1 V。根據式(10)可得總驅動力F=0.828 3 V,而待檢測二次諧波信號的幅值為a=(F-F0)/λ=(0.828 3-0.826)/0.2=0.011 5 V。

2.2 隨機噪聲對檢測結果的影響

將待檢測信號加入一定信噪比的噪聲n(t),S′=ηS+n(t),當信噪比SNR分別為20、0.5、-9.5和-16.5時,包含噪聲的待測信號輸入至第2個杜芬振子,4種信噪比下杜芬振子相圖如圖4所示。

觀察組總有效率93.10%（54/58），高于對照組的75.86%（44/58）（P＜0.05）。見表1。

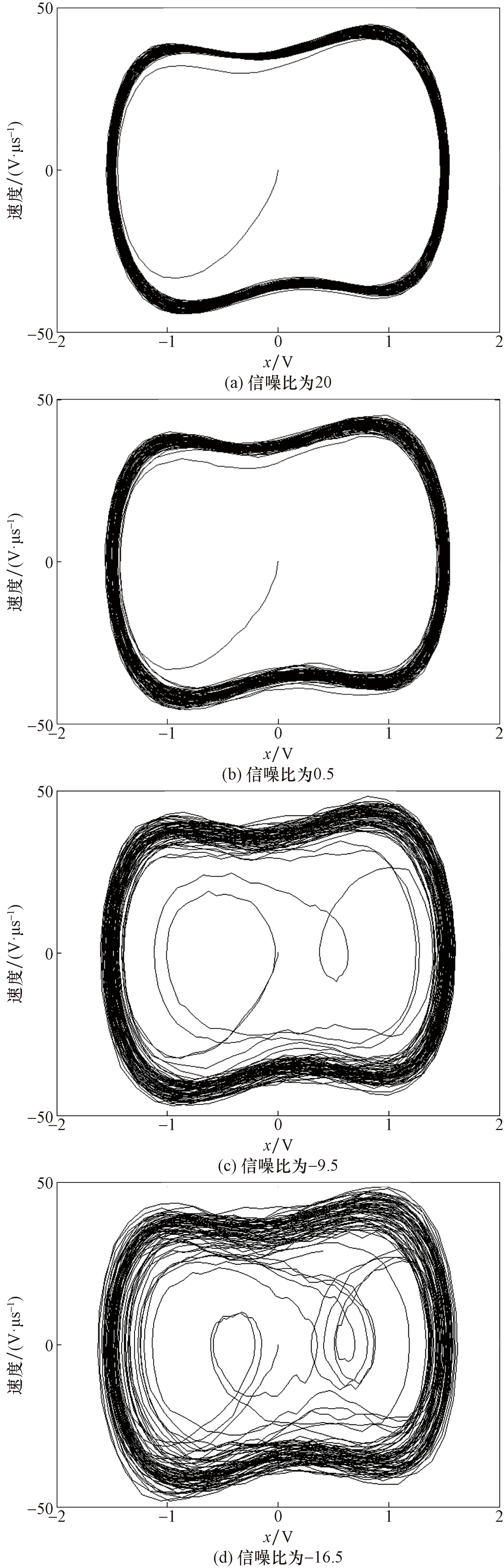
圖4 含噪聲待測信號相圖Fig.4 Duffing phase of noisy detected signal

由圖4可知,當不同信噪比的待測信號輸入杜芬檢測振子時,4個相圖變為大尺度周期狀態,說明超聲非線性輸出信號中含有4.8 MHz的二次諧波信號,即杜芬振子可以將湮沒在隨機噪聲下的二次諧波信號檢測出來。通過對比4個相圖可以發現,隨著噪聲強度的增加,相圖的軌跡越來越粗糙,相軌跡的穩定性變差,這是因為Duffing振子系統對噪聲有一定的免疫能力,但是隨機噪聲的方差會影響相軌跡的粗糙程度。

3 結論

利用杜芬方程對超聲非線性輸出信號的二次諧波進行檢測,得到如下結論。

(1)對常規杜芬振子進行頻率轉換、分析待測信號和驅動力信號初始相位對檢測結果的影響、對待檢測信號進行變尺度等操作,得到能檢測實際工程信號的杜芬陣列檢測模型。

(2)利用杜芬陣列對超聲非線性輸出信號的二次諧波信號進行檢測,首先對超聲非線性輸出信號進行變尺度變換,使杜芬陣列與超聲非線性輸出信號匹配;當變尺度的超聲非線性輸出信號輸入杜芬陣列時,第二個杜芬振子相圖軌跡由混沌狀態過渡至大尺度周期狀態,微弱的待檢測信號能夠被檢測出來。

(3)根據杜芬振子總驅動力幅值和響應信號幅值之間的對應關系,能夠有效估算出二次諧波信號的幅值。