融合VMD和GRU模型的城市道路行程時間預測方法

李世杰, 王景升, 牛帥

(中國人民公安大學交通管理學院, 北京 100038)

城市交通問題是城市發展過程中不可回避的問題,隨著汽車保有量逐漸增加,城市道路交通流量進而逐漸增長。行程時間作為反映道路運行狀況的重要指標,可以衡量道路的通行效率[1]。行程時間在城市交通出行誘導起著關鍵作用,通過預測未來道路行程時間,可以為交通參與者提供路徑選擇。如何對行程時間進行預測是研究緩解城市交通壓力的主要熱點和難點,因此精準預測行程時間對于道路交通誘導至關重要[2]。

近年來,隨著智能交通系統和人工智能技術的迅速發展,交通預測成為城市交通領域的熱點之一。中外學者提出的預測方法可以從以下角度進行分類。分別為基于統計模型、基于機器學習模型和基于深度學習模型等預測方法。基于統計的預測方法主要有線性回歸、ARIMA(auto-regressive integrated moving-average model)模型[3-4]、 Kalman(Kalman filter) 濾波[5]等方法,由于實際交通具有非線性和混沌特性,此類模型通常依賴于數據平穩的假設,且不適應大規模數據處理。機器學習模型的預測方法主要有支持向量機[6]、貝葉斯網絡[7]、XGBoost(extreme gradient boosting)[8]、K近鄰算法[9]等。Long等[10]使用人工魚群算法對SVM(support vector machine)模型進行優化,將優化后的SVM模型用于高速公路行程時間預測,能夠獲得較高的準確率。Meng等[11]將KNN(k-nearest neighbors)與SVM模型結合對高速公路行程時間進行預測,能夠在加速訓練的同時保證預測的準確性。基于深度學習模型的預測方法如長短期記憶(long shot-term memory, LSTM)[12]、門控循環單元(gated recurrent unit, GRU)[13]等。Li等[14]使用基于LSTM的卷積神經網絡對時空特征進行學習以準確預測道路行程時間;張明等[15]將改進注意力機制與GRU模型結合預測城市道路行程時間,預測精度相較于僅使用GRU模型有較大提高;雖然深度神經網絡模型與機器學習模型相比,在處理大規模數據時具有顯著優勢,但由于行程時間序列具有較強的非線性和非平穩性,單一神經網絡在預測精度越來越難以滿足出行者與交通管理著日益增長的精度需求。與單個模型相比,組合模型[16]能夠提供更加準確的預測結果。

因此,現借鑒金融學和地理學等領域中廣泛應用的自適應信號分解方法(variational mode decomposition,VMD)[17],將原始行程時間序列進行分解,以降低原始時間序列的非穩態性。考慮到GRU模型在時間序列預測中具有較高的精度,提出一種新的組合預測模型,簡稱VMD-GRU,以實現對非平穩性較強的行程時間進行預測。

1 基本原理

1.1 VMD原理

變分模態分解(VMD)是一種能夠有效處理波動信號的自適應信號分解算法,可以有效降低復雜度高和非線性較強的時間序列非平穩性[18]。VMD將原始時間序列進行分解為若干個相對平穩且不同頻率的時間子序列,以減少模態混疊現象的發生。VMD算法流程如下。

步驟1構造變分模型。將原始序列分解為K個分量,構造其約束變分函數為

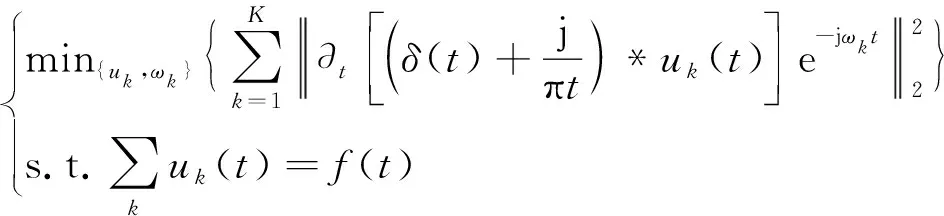
(1)

式(1)中:K為模態數目,即分解信號的個數;uk(t)為第t個模態分量;ωk為中心頻率;k為第k個分解信號;?t為隨著時間變化的偏導數;δ(t)為狄克拉分布函數;f(t)為原始序列信號;*為卷積;j為虛數單位;t為時間參數。

步驟2利用其約束變分模型引入拉格朗日乘子和二次懲罰因子來降低干擾,同時將上述問題轉化為非約束變分問題。

(2)

式(2)中:L為增廣Lagrange函數表達式;α為二次懲罰因子;λ為拉格朗日因子。

步驟3使用交替方向乘子法進行求解,中心頻率ωk與模態uk的求解公式為

(3)

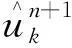
1.2 GRU模型

門控循環網絡(GRU)是應用最為廣泛的循環神經網絡(recurrent neural network,RNN)變種之一,同時作為LSTM的改進版,使用“門”結構選擇性地丟棄或保留一些信息,在某些情況下能產生較為優異的效果。GRU包含更新門和重置門兩個門結構,它將LSTM模型中的3個門合并成更新門和重置門,其更新門相當于LSTM的輸入門和遺忘門,結構變得更加簡單,從而相對于LSTM提高了模型整體的訓練速度。

GRU模型結構如圖1所示。更新門幫助模型決定要將多少前一時刻的信息傳遞到當前時刻中,更新門的值越小,代表更少的前一時刻信息被傳遞到當前時刻;重置門用于控制遺忘前一時刻信息的程度,重置門的值越小,代表忽視前一時刻的信息越多。

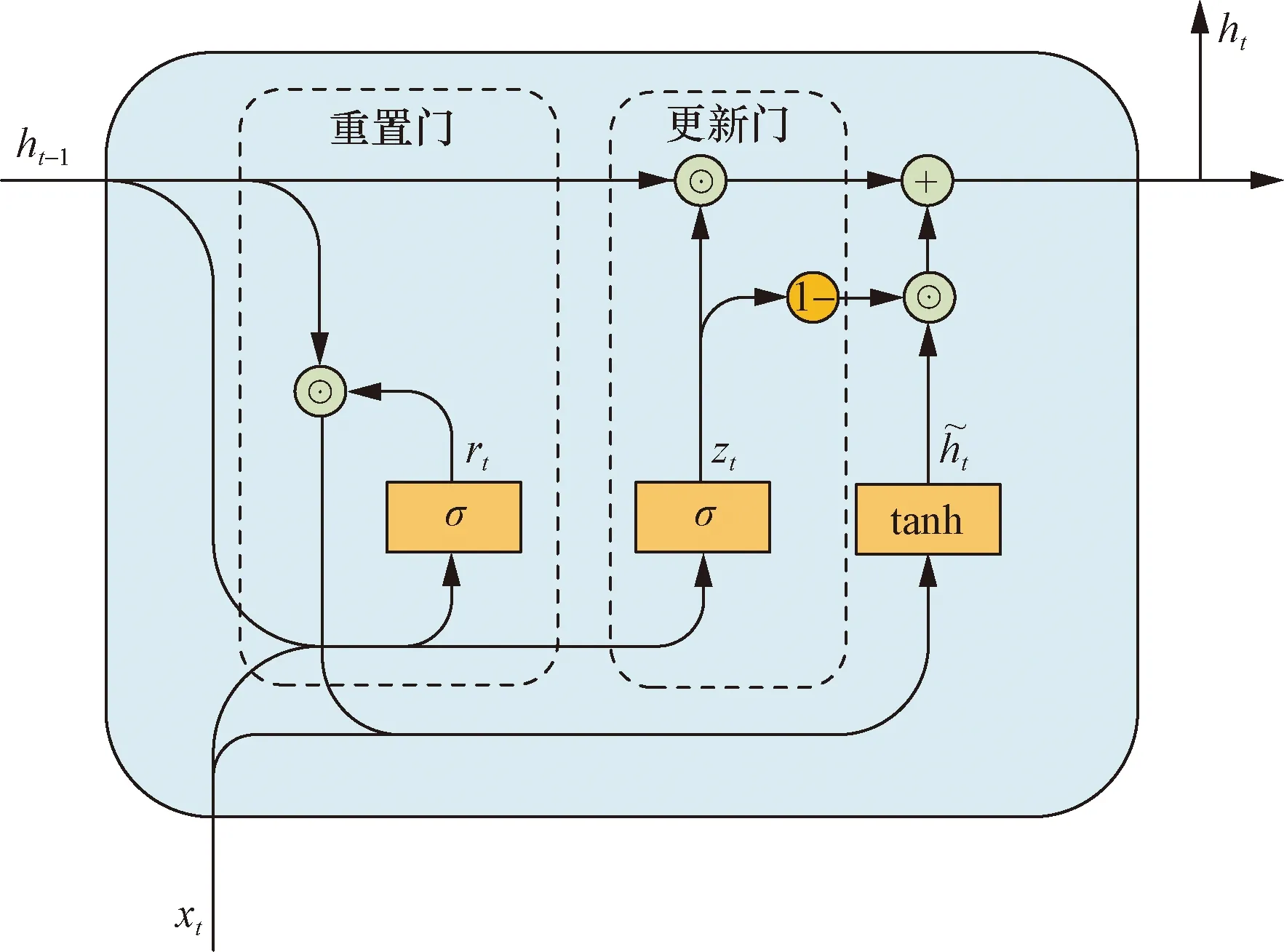
圖1 GRU內部結構Fig.1 Internal structure of GRU

zt=σ(Wz[ht-1,xt]+bz)

(4)

rt=σ(Wr[ht-1,xt]+br)

(5)

(6)

(7)

式中:zt和rt分別為GRU的更新門和重置門;xt為t

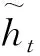
2 VMD-GRU組合預測模型

行程時間序列具有非平穩性與波動性等特點,使用單一的預測模型難以得到較精準的預測結果。考慮到VMD分解算法在處理非線性數據方面的優勢以及GRU模型能夠較好地捕獲時間序列的特征。文本使用VMD-GRU組合模型對行程時間進行預測。VMD-GRU組合預測模型首先將原始行程時間序列分解為若干相對平穩且不同頻率的時間子序列,實現行程時間序列的降噪,有效緩解原始序列的非平穩性與波動性,其次針對其子序列建立預測模型,通過使用GRU模型獨立預測若干時間子序列使預測風險分散,最后將各個時間子序列的預測結果進行融合。為了更好地捕獲城市道路行程時間序列的非線性和非平穩特征,通過使用VMD算法將原始行程時間序列分解為若干相對平穩的IMF(intrinsic mode function)分量,然后為每個IMF分量構建GRU預測模型,最后將每個IMF分量預測的結果進行匯總融合,以產生最終行程時間預測結果。設計城市道路行程時間VMD-GRU組合預測模型如圖2所示。VMD-GRU組合算法的具體步驟如表1所示。

表1 VMD-GRU模型的預測步驟Table 1 The prediction steps of the VMD-GRU model

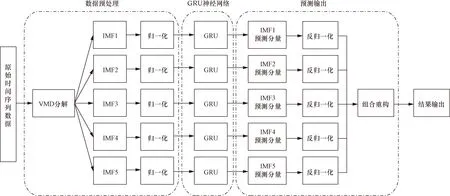
圖2 VMD-GRU模型流程圖Fig.2 VMD-GRU model flowchart

3 實例分析

3.1 數據描述

本文數據來源于河北省唐山市北新西道部分路段電子警察卡口數據。該數據包含交叉口編號、交叉口名稱、車牌號、采集時間、方向編號等字段屬性。通過提取上下游交叉口電子警察過車記錄,計算15 min時間間隔內車輛經過上下游交叉口的行程時間,然后對行程時間進行清洗,剔除異常值,最后對15 min時間間隔內的行程時間取均值,作為下文行程時間的訓練與預測數據集。經數據處理后,得到行程時間樣本數據,為連續12 d的15 min粒度構成的時間序列,共計1 152段行程時間數據,如圖3所示。

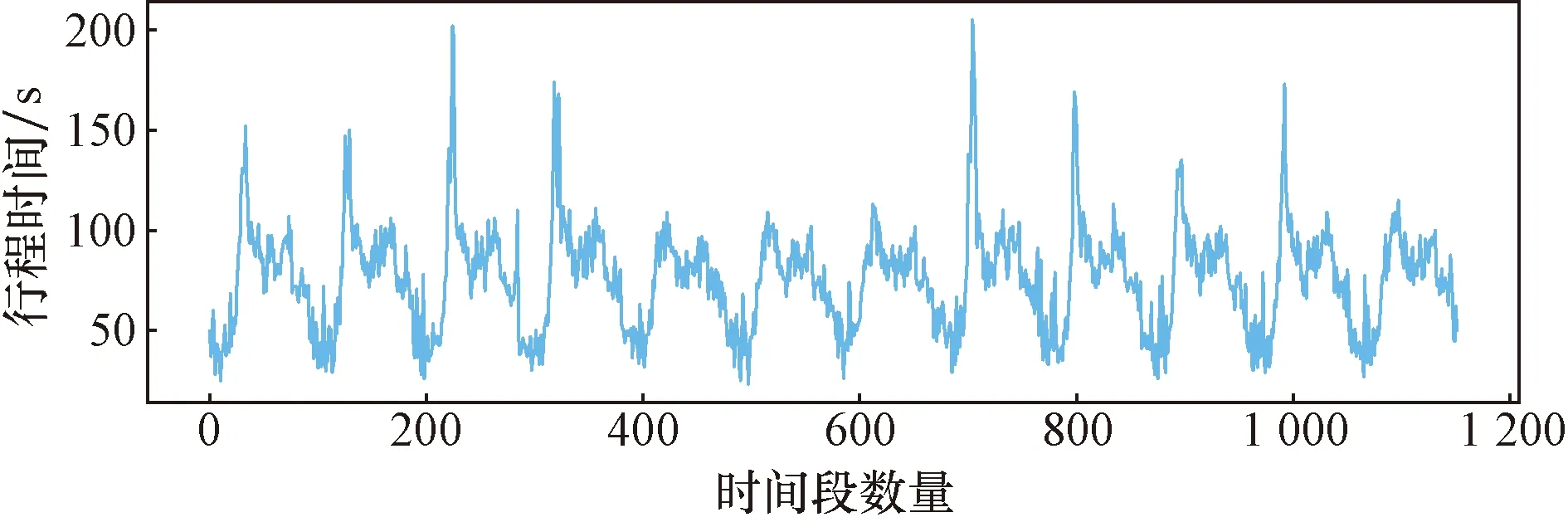
圖3 行程時間序列圖Fig.3 Travel time series plot

3.2 基于VMD的行程時間序列分解

將行程時間序列采用VMD算法分解為5個IMF時間子序列分量,降低原始時間序列的復雜程度,分解后的時間子序列圖像如圖4所示。

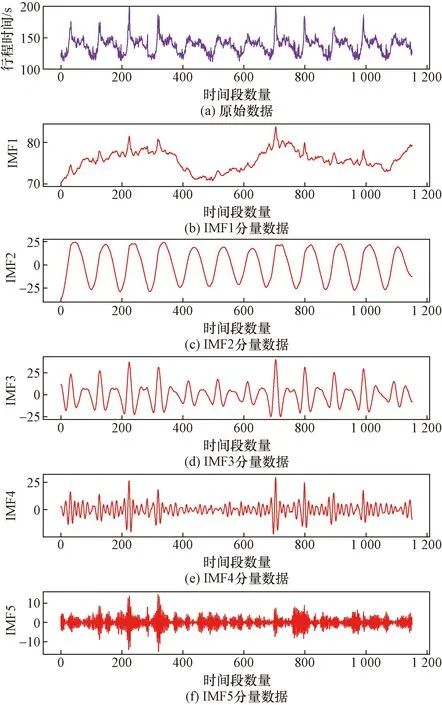
圖4 行程時間序列分解結果Fig.4 Travel time series decomposition results

3.3 基于VMD-GRU模型的預測結果

為有效驗證模型的預測效果,將數據集前80%作為訓練集,后20%作為測試集。為消除數據量綱所帶來的影響,將VMD分解后的時間子序列數據分別進行歸一化處理,并分別使用GRU、LSTM模型對其進行預測。在GRU神經網絡中,GRU層包含80個神經元,Dropout層可隨機斷開網絡層之間的連接,有效防止過擬合,經過多次實驗,設置為0.3時效果較好,滑動時間窗口長度設置為60,損失函數選用均方誤差,使用Adam優化器對模型參數進行優化,迭代次數設置為50,Batch_Size設置為32。為進行組合模型對比驗證,在LSTM神經網絡預測模型中,僅將GRU層改變為LSTM層,其余設置不變。為檢驗模型預測效果,采用均方誤差(mean squared error,MSE)、均方根誤差(RMSE)、平均絕對誤差(MAE)作為評價指標。

(8)

(9)

(10)

式中:xit為時間序列的真實值;xip為時間序列的預測值;n為數據個數。

VMD-GRU模型與VMD-LSTM模型的各分量IMF的預測對比結果如表2所示。從表2可以看出, GRU模型中各個分量的MSE、RMSE、MAE值均小于LSTM模型中的值,其中MSE降低0.05～0.50,RMSE降低0.10～0.26,MAE降低0.07～0.21。說明GRU模型在預測時間子序列的預測精度高于LSTM模型,這是因為GRU模型具有獨特的門結構特征,能夠有效地學習各分量的數據特征,提高模型訓練速度與預測精度。

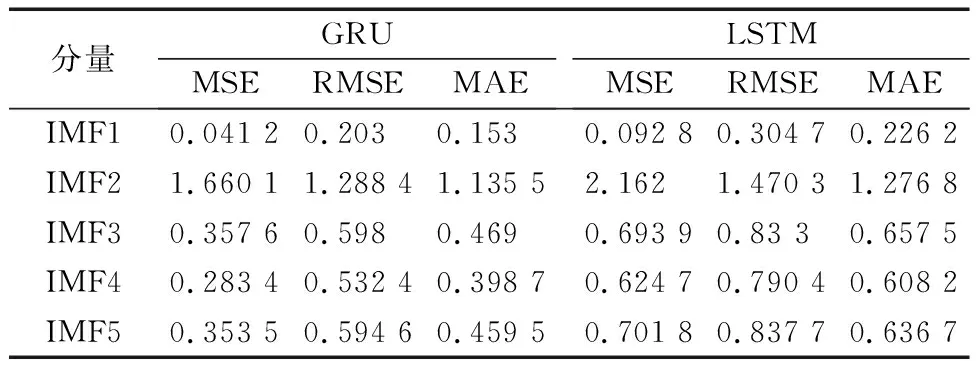
表2 各分量IMF預測評價結果Table 2 Each component of the IMF predicted evaluation results

為了驗證VMD-GRU組合預測模型的精確性,將單一的RNN、LSTM、GRU、BiLSTM神經網絡模型以及VMD-LSTM模型作為對照組,對行程時間序列進行預測,各個預測模型輸出的測試集擬合結果如圖5所示,各個模型相應的RMSE、MSE、MAE值如表3所示。

表3 各模型評價結果Table 3 Evaluation results of each model

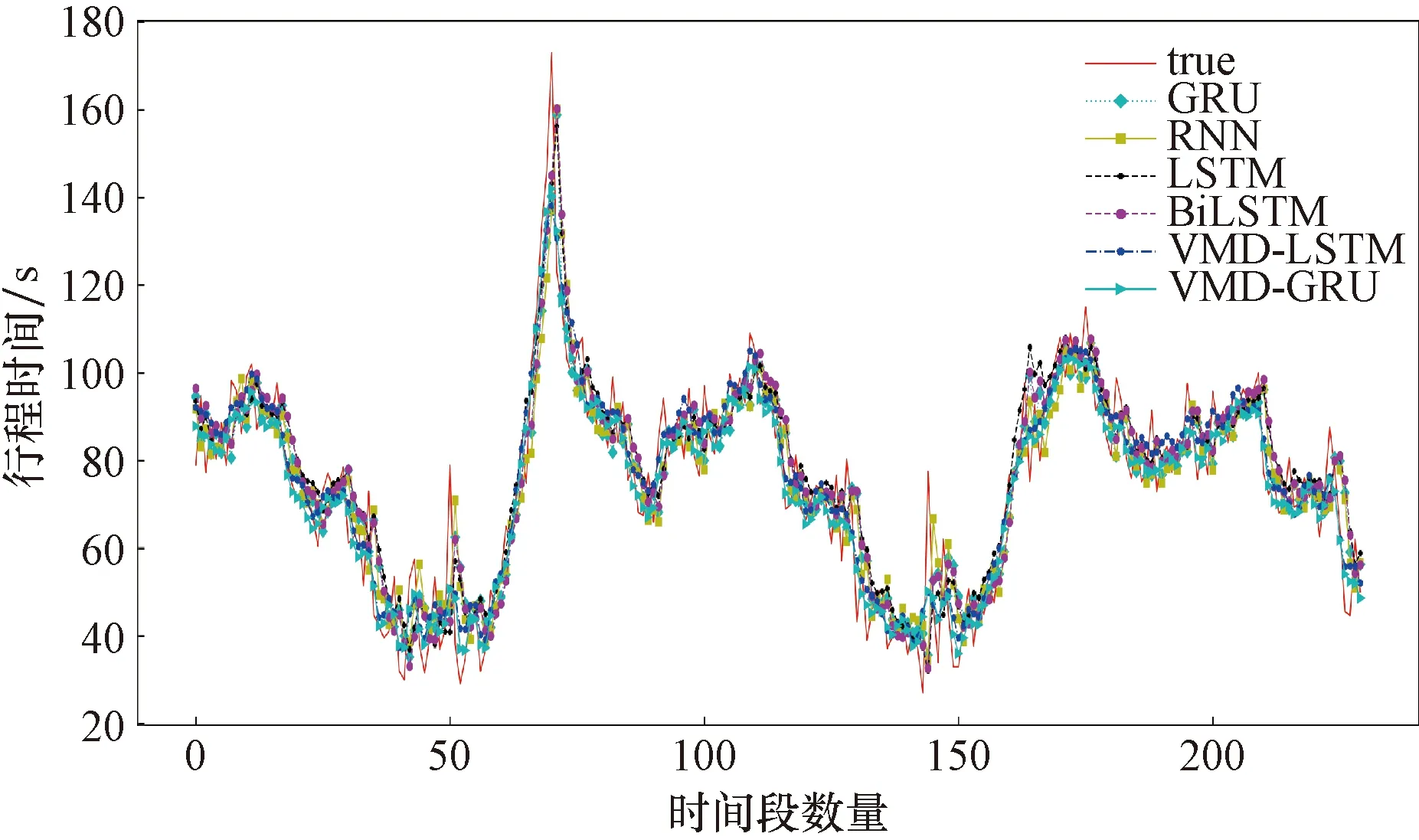
true表示實際的行程時間數值圖5 各模型預測結果Fig.5 Predicted results of each model

由圖5可知,VMD-GRU組合預測模型的擬合曲線與真實值的吻合程度較高。由表2可知,組合模型相較于單一模型預測精度提升較大,說明組合模型能更好地捕獲行程時間的變化,比單一模型適用于波動性較強的城市道路行程時間預測。主要原因是使用VMD分解算法后,可以有效降低原始行程時間序列較強的非線性特征,使得模型在訓練時能夠更容易捕獲其特征,從而提高預測精度。VMD-GRU組合預測模型的RMSE、MSE、MAE、MAPE值相較于其他模型均較低,其中MSE降低4.81～79.98,RMSE降低0.34～4.37,MAE降低0.22～3.35。表明VMD-GRU模型在行程時間序列預測中相較于其他對照模型具有優越性。

4 結論

城市道路行程時間序列具有非線性、非平穩性,因此單一預測模型較難達到滿意的預測結果。提出了融合VMD與GRU的行程時間組合預測模型,將原始時間序列分解,并分別與門控循環單元神經網絡結合,最后將各自預測的結果進行融合,產成最終的行程時間序列預測結果。通過實例得出以下結論。

(1)通過使用VMD算法將原始行程時間序列分解為5個IMF分量,能夠有效降低了原始時間序列的波動性。

(2)使用VMD-LSTM模型作為對照組,來證明VMD-GRU模型在處理行程時間子序列具有較高的預測精度。

(3)將RNN、LSTM、GRU單一模型和VMD-LSTM模型的行程時間預測結果與本文所提出的VMD-GRU模型進行對比驗證,證明VMD-GRU模型在行程時間預測中的優越性。

但城市道路行程時間仍受交通環境、天氣、道路狀況等因素的影響,下一步考慮將獲取相關因素的數據,在預測時綜合考慮相關因素的影響。