基于深度強化學習的大型活動關鍵交叉口信號控制

宋太龍, 賀玉龍, 劉欽

( 北京工業大學北京市交通工程重點實驗室, 北京 100124)

大型活動的舉辦會給場館周邊路網帶來具有時段性特點的交通壓力,為保證活動的順利舉辦,需要對活動場館周圍的路網進行交通管制。交通信號控制作為一種可以在時間以及空間上分配路權的控制方式,設置合理而有效的配時方案不僅可以降低車流的行駛延誤,更可以保障區域路網的正常運行,而路網中關鍵交叉口的高效有序運行又是保證整體路網正常運轉的關鍵[1],當關鍵交叉口發生擁堵或混亂時,將對周圍道路產生負面影響并導致路網通行效率大幅降低,因此針對活動場館周圍關鍵交叉口的交通信號進行有效控制具有重要意義,活動場館周圍關鍵交叉口運行狀態的優劣不僅影響了大型活動是否可以順利舉辦,同時也決定了大型活動條件下路網運行狀態的好壞。

相比于日常生活,大型活動舉辦時期的交通量變化更為迅速,短時聚散現象明顯,流量波動大,乘坐公共交通出行需求上升。傳統的信號控制方案僅針對各進口道排隊信息,沒有差異性分析日常出行與大型活動出行的出行特性。

現針對大型活動下的交通出行特征,分析大型活動相關出行者的交通需求,構建以大型活動為背景的場館路網關鍵交叉口信號控制方法,在建模過程中,考慮到大型活動的交通運行特點,如短時內人群聚集數量大,搭乘公共交通人數多的特點,通過將信控優化過程中的關鍵指標從傳統的車均延誤、停車次數設計為不同出行方式的時間損失,公共交通排隊時間等指標,從乘客出行延誤的角度出發,在信號配時方案中將保障活動參與者的優先權,并以各進口道排隊時間以及交叉口單位時間內的停駛車輛數作為評價交叉口信號配時方案好壞的關鍵指標,結合三者共同構建以深度強化學習算法-A2C(advantage actor critic)方法為基礎的信號控制模型,并將傳統的定時控制方法以及其他深度強化學習,如Q-learning、DQN算法作為實驗對照組,驗證模型的優勢。

1 交叉口信號控制研究

隨著計算機計算水平以及信息檢測技術的提高,目前針對交叉口的信號控制理論研究已經具備了一定的深度,從傳統的定時控制發展到基于檢測器的感應控制,并逐漸發展到基于實時大數據的自適應控制。

傳統的定時控制比較經典的是Webster法、美國的HCM法燈[2];定時控制的方法好處在于可以根據調查得到的歷史流量數據,計算不同時段的最優周期以及信號配時并長期產生較好的控制效果。但該方法無法適應短時變化的交通流,且沒有充分利用交通流運行的時空規律,導致綠燈時間的空放現象發生。

感應控制相比定時控制更多的是對道路使用情況信息的檢測。借助檢測器對道路使用情況進行檢測,并根據監測數據做出信號燈時長或周期的調整,達到降低交叉口延誤的目的。

相比于固定配時和感應配時,自適應交通信號控制方法提高了信號燈的靈活性以及信號控制效率[3],強化學習作為一種可以通過當前環境狀態尋求最優控制動作的自適應控制算法,可以很好地通過交叉口的運行狀態信息,如交叉口的排隊情況、流量大小等,選取應用于下一階段的最優信號配時,達到降低交叉口整體延誤的效果。在自學習算法方面,Q學習算法、SARSA算法是最早一批在交叉口信號控制領域進行應用研究的強化學習方法[4]。宋國治等[5]使用深度Q-learning算法對交叉口進行信號燈配時優化,實驗證明,深度Q-learning算法下的信號控制相比于定時控制單車延誤更小,綠燈利用率更高;白靜靜等[6]考慮到SARSA算法在目標選擇策略中既考慮新狀態下的最優獎勵又考慮新狀態所帶來的風險,因此將其應用于交叉口配時中,結果表明SARSA算法的配時優化效果高于Q學習;李振龍等[7]使用排隊消散指數對交通狀態進行描述,通過對排隊閾值的設計,提高智能體對狀態變化的敏感性,達到有效控制的目的。

然而,強化學習直接應用于大型交叉口交通信號燈控制會由于環境變化較為復雜導致模型復雜度過高,因此后續研究中逐漸使用深度學習與強化學習結合的方式構建深度強化學習方法[8],達到既可以有效提取交叉口環境的抽象運行狀態,又可以準確高效的選取最優動作以進行信號相位以及綠燈時長的優化,強化學習方法應用于信號控制的控制流程如圖1所示。

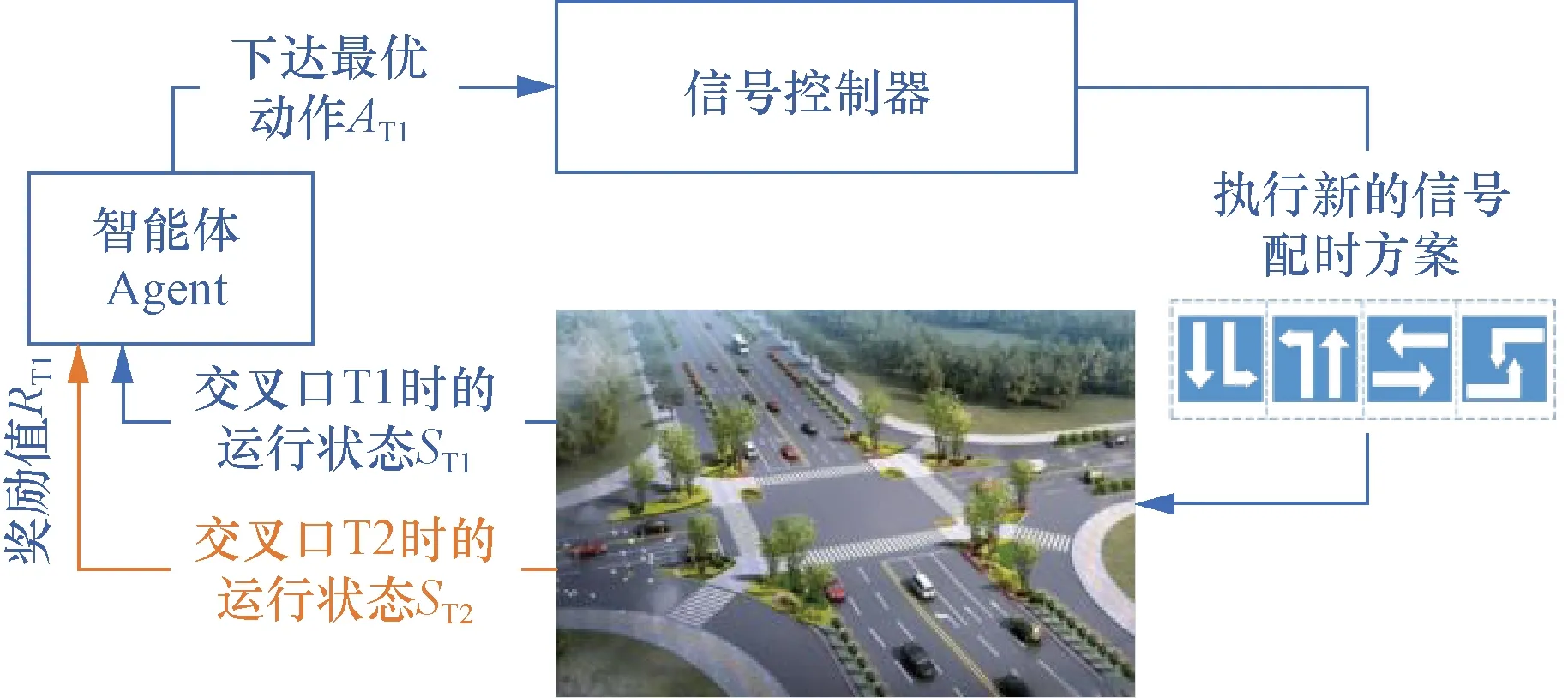
圖1 基于強化學習方法的交叉口信號控制流程Fig.1 Signal control flow of intersection based on reinforcement learning method

傳統的考慮大型活動的自適應控制方法通常將交叉口內各進口道的檢測信息作為環境信息,將車均延誤、停車次數以及排隊長度作為評價交叉口運行狀態的指標[4],并依此建立信號交叉口最優控制模型,求解最優配時方案。賈彥峰等[9]考慮關鍵路口可能發生的排隊溢流現象,提出線軸結合方法優化過飽和交叉口的信號相位,以達到緩解某運行方向排隊過長的情況。Li等[10]將交叉口各進口道的隊列長度、車輛運行速度定義為狀態信息,將車輛的累計延誤定義為獎勵,構建了基于DQN(deep Q-network)算法的交叉口信號控制方法,實驗證明該方法相比為Webster法、Q-learning算法效果更優,車輛延誤更低。傳統的交叉口優化方案往往以交叉口整體運行效率為目標,在大型活動舉辦期間,如果僅從各進口道流量進行考慮,不針對分析活動參與者的出行特征以及大型活動相關的車流與社會車流差異性,則構建的信號控制方案是無法適配活動場地周邊實際交叉口的出行者通行需求。

2 考慮大型活動特征的A2C信號優化模型

2.1 大型活動交通流運行特征

大型活動場館周圍的路網交通流運行特征變化主要有以下特點:①需求產生時間集中且需求量較大;活動開始以及結束時間場館周圍路網的壓力會顯著性變化,流量隨時間變化曲線如圖2所示;②公共交通出行量增加;參加活動的群眾以及志愿者普遍采用公共交通作為自己前往活動場館的出行方式,媒體、部分活動參與者會乘坐活動大客車前往場館[11];③擁堵存在方向性特征。

圖2 流量隨時間變化曲線Fig.2 Variation curve of flow over time

2.2 基于A2C算法的信號控制模型構建

A2C算法是在原AC(actor-critic)算法的基礎上,對A3C(asynchronous advantage actor critic)算法的改進版本,A3C算法基于異步強化學習思想[12],在原AC算法的基礎上加入異步操作,使多個AC結構網絡同步運行,但工作組過多導致的內存問題以及環境的初始化不同步,從而使得部分數據存在冗余。A2C算法采用并行架構,每個工作組都會獨立的與自己的環境進行交互,且不再依賴于運行效率較低的經驗池結構,避免了由經驗池抽樣不均勻導致的學習經驗存在偏置的問題,A2C的算法架構如圖3所示 。

Update Collector用于收集參數的更新;Agent為智能體圖3 A2C算法架構及交互方式Fig.3 Advantage actor critic algorithm architecture and interaction mode

在本文模型的構建過程中,考慮大型活動背景下出行者數量大且采用公共交通出行的特點,在獎勵函數的構建過程中,將公交車、小汽車等車型的等待時間作為參數,其中,將降低公交車出行延誤以及等待時間作為主要影響參數;Agent根據當前交叉口環境所提供的各進口道交通狀態信息State,執行信號方案,并依據獎勵函數的計算值調整動作的執行,以保證智能體在放行方案的選取上實現公交優先,優先滿足大型活動出行者的出行需求。

2.2.1 交通狀態構建

狀態空間是智能體做出動作前可觀測到的基礎信息,智能體基于狀態信息選擇最優動作[13]。

因此狀態空間的構建應盡可能全面且有效地表示交叉口的運行狀態,既要保證信息復雜度較低,也要保證信息的有效性較高,復雜多變且冗余信息較多的狀態空間會導致算法無法高效運行[14]。

在狀態空間的構建中,狀態信息在傳統的各進口道流量信息的基礎上,將各車道的排隊情況以及公交車數量考慮在內;狀態矩陣構建由以上信息組成,狀態空間大小m(2+L/C),其中,M為車道數,L為檢測區域長度,C為網格長度,檢測網格內存在車輛即為1,否則為0,本文實驗中,進口道車道數為22,檢測區域長度為60 m,網格長度5 m,狀態空間大小22×14。狀態空間示意圖如圖4所示;相比于直接以照片形式將交叉口圖像信息作為狀態描述的方式更能有效降低狀態復雜度,達到降低數據維度、去除冗余信息,加快模型收斂的目的。

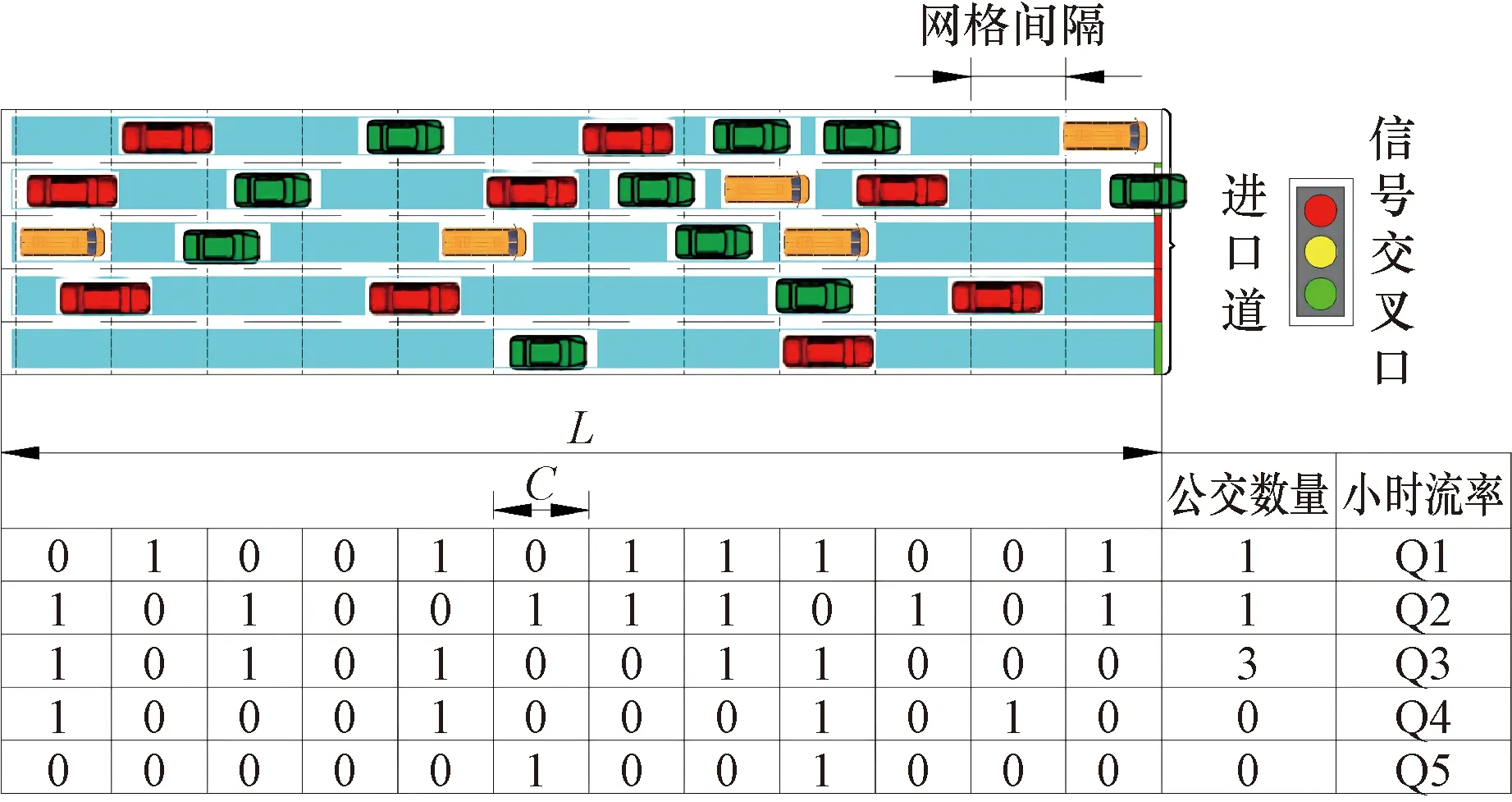
Q1～Q5為每車道的小時流率圖4 狀態空間示意圖Fig.4 Schematic diagram of state space

2.2.2 動作空間構建

為保證信號控制過程中滿足行人過街時長以及減少綠燈時間設置不合理情況的發生,對模型中交叉口最小綠燈時間以及最大綠燈時間進行約束,從而減少頻繁切換相位導致的非穩態交通系統情況發生。

基于強化學習的信號控制中動作主要設為以下兩種。

(1)切換相位。將動作空間設置為{0,1},即智能體通過選擇是否切換相位作為動作達到對交叉口信號時長的控制,動作的選擇往往間隔一定時長[15]。

(2)調整綠燈時長。將信號燈各相位的時長默認為最小綠燈時間,智能體通過對當前相位綠燈時間是否延長t秒作為動作的選擇[16],即該相位綠燈時間增加t秒或維持不變,且綠燈時長最大不能超過最大綠燈時間。

本文中智能體的動作設置為對當前相位綠燈時長的調整,進行如下設計。

(1)動作空間由信號放行相位組成,其大小={phase1,phase2,phase3,phase4},當該相位綠燈時間達到最小綠燈時長時,Agent進行動作選擇,并從4個信號相位中選擇一個放行相位,若與當前放行相位一致,則持續時間1 s;智能體下一動作選擇為1 s后[17];

最小綠燈時間Gmin的計算公式為

(1)

式(1)中:LP為人行橫道寬度;VP為滿足行人過街的平均速度;I為綠燈間隔時間。

(2)當顯示綠燈時間不足最小綠燈時間時,智能體無法采用動作將信號切換至下一相位;當顯示綠燈時間達到最大設計時長時,強制切換值下一相位。

(3)切換相位時,進行3 s的黃燈顯示,并重新判定當前綠燈時長是否滿足最小綠燈時間。

將動作空間設置從切換相位與否修改為連續性的調整綠燈時長,雖然增加了模型復雜度,但是提高了綠燈時間的利用率。

2.2.3 獎勵函數構建

獎勵函數是指智能體在觀測交叉口交通狀態并根據狀態信息采取動作后得到的反饋值[18],即交叉口信號配時變化產生影響的一個判定值,該值用于判定當前交通狀態下采用該信號相位的一個好壞程度,在強化學習處理交叉口信號控制的問題中,獎勵函數通常選擇累計等待時間、累計延誤、某一主要進口道的延誤、實際車速與車道限速的差值或停車次數等指標。

考慮到大型活動舉辦過程中,活動參與者大多數采取公共交通且需要保證參加活動的準時性的特點,因此對關鍵交叉口進行信號優化控制建模時,針對獎勵函數進行如下設計,獎勵函數的指標包括不同車型的平均損失時間,公交排隊等待時間、各進口道停駛車輛數、交叉口總延誤等[19]。

考慮出行者不同車型的平均損失時間Dp計算公式為

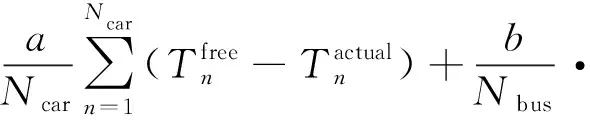
(2)

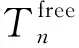
(3)

單位時間內停駛流量計算公式為

(4)

交叉口總延誤計算公式為

(5)

2.2.4 動作選擇策略

智能體在動作選擇過程中,通常根據Q值,采用貪婪算法以保證每次智能體都會選取到以獲取獎勵更多為目的的動作[20],但僅采用貪婪算法可能會導致算法迭代過程中動作的選擇方案陷入局部最優解。

針對此情況,采用動態ε-greedy策略,在動作的選擇過程中,將智能體隨機選擇下一階段信號相位的可能性定為ε,將選取當前最優信號相位的可能性定為1-ε,且隨著迭代次數的增加,ε值逐漸減小,即為保證訓練過程中不會陷入局部最優解,智能體會隨著迭代次數的增加,隨機選取信號方案的概率降低,選擇可以獲取更多獎勵值的信號相位的可能性增大。計算公式為

(6)

式(6)中:εm為下一仿真步中,動作選擇時的隨機探索概率;εmin為根據經驗設置的最小值;εcurrent為當前仿真步中動作選擇時的隨機探索概率;m為當前仿真步數;M為總仿真步數。

算法引入優勢函數思想,優勢函數計算公式如式(7)所示,通過對比動作價值函數Qπ(s,a)計算的值與狀態價值函數Vπ(s)值的大小,評價Agent采用當前信控相位相比于其他信控相位的優勢大小,帶有神經網絡的動作價值函數Q(s,a,w)以及帶有神經網絡的狀態價值函數V(s,w)計算公式如下。

Aπ(s,a)=Qπ(s,a)-Vπ(s)

(7)

Q(s,a,w)≈qπ(s,a)

(8)

(9)

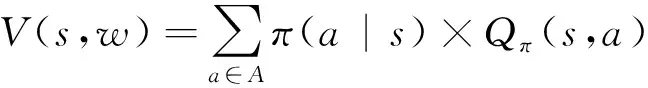
(10)

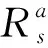
算法的損失函數為

(11)

式(11)中:LA2C(w)為A2C算法的損失函數;v(st,w)為使用神經網絡計算的t時刻的狀態價值函數值,使用梯度下降更新參數w。

3 仿真實驗和實驗結果

3.1 案例分析

選取SUMO(simulation of urban mobility)軟件作為交通仿真的搭建平臺,通過設計道路網絡模塊及構建交通需求模型,并借助Traci接口進行檢測器設計以及算法交互,完成仿真實驗的設計。本文以北京市海淀區首都體育館為活動場館選取周邊大型交叉口構建仿真實驗場景。

3.1.1 交叉口進口道分布情況

以中關村南大街與西直門外大街輔路所構成的交叉口為實驗場地,交叉口渠化情況如圖5和圖6所示。該交叉口為典型的四岔結構,東西向與南北向同為5進口道,4出口道的配置,其中東西向左轉專用車道與直行車道以及右轉專用車道比例為2∶2∶1;北進口道在臨近路口停車線時最右側借助道路拓寬手段增加右轉空間,為簡化模型,左轉專用車道與直行車道以及右轉專用車道比例設置為

圖5 首都體育館周邊交叉口實景圖Fig.5 Real scene of intersection around Capital Gymnasium

2∶3∶1;南進口道簡化為左轉專用車道與直行車道以及右轉專用車道比例為2∶3∶1;各方向進口道車道分布情況如表1所示。

表1 交叉口進口道車道分布情況Table 1 Lane distribution of entrance road at intersection

3.1.2 各進口道流量特征

為保證實驗具有一定的實際意義且不受疫情封控及其他管控因素的影響,選取2019年西直門外大街-中關村南大街交叉口高峰時段實際調查流量作為輸入,流量調查表如表2所示。

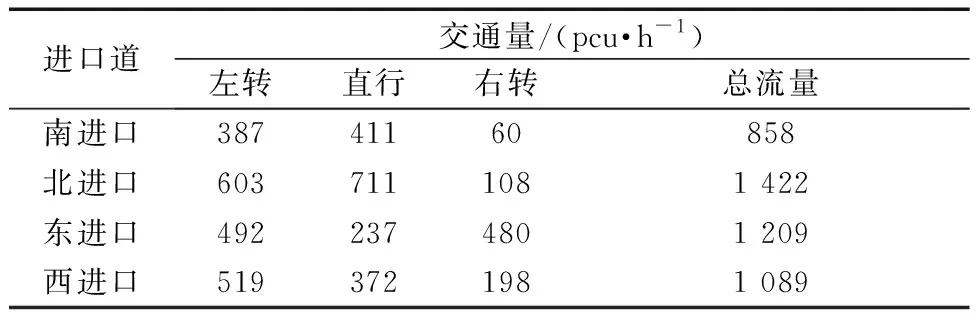
表2 交叉口實際調查交通量Table 2 Actual investigated traffic volume at intersection

3.1.3 現狀基礎信號配時

選取晚高峰(17:00—19:00)時段對交叉口信號燈配時進行調查,現狀配時方案如表3所示。交叉口初始信號相位如圖7所示。

表3 中關村南大街-西直門外大街輔路交叉口現狀信號配時方案Table 3 Current signal timing scheme of Zhongguancun South Street-Xizhimenwai Street Auxiliary Road intersection

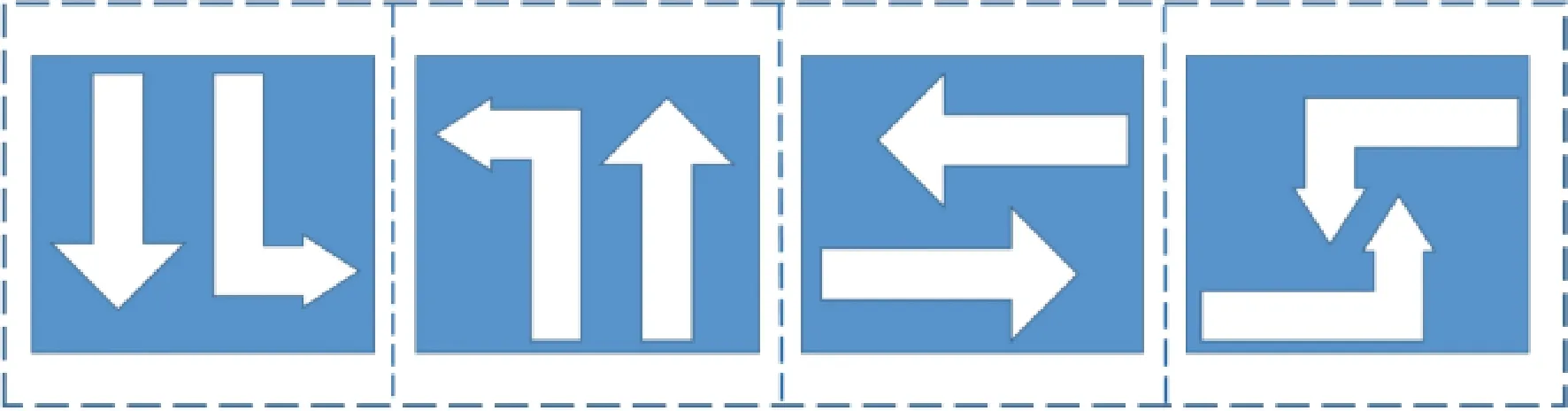
圖7 交叉口信號相位示意圖Fig.7 Phase diagram of intersection signal

3.2 設計及仿真結果分析

本文算法參數設計如表4所示。

表4 實驗參數設置Table 4 Experimental parameter settings

為驗證本文模型的準確性以及有效性,本文分別選擇不同類型的信號配時作為對照試驗,對照試驗組如表5所示。

表5 對照實驗組Table 5 Control experimental group

單次仿真步為100 000個時間步,共計200萬仿真步。針對不同方案的仿真實驗,實驗結果如圖8～圖12所示。

圖8 所有實驗迭代過程中獎勵收斂情況Fig.8 Reward convergence in all experimental iterations

由圖8可知,無論是收斂的效率、模型訓練過程中的穩定性還是獎勵值的獲取,本文所構建信號控制方法總是優于DQN算法以及Q-learning算法的控制效果。

本文算法的policy loss與value loss的收斂過程如圖9所示。

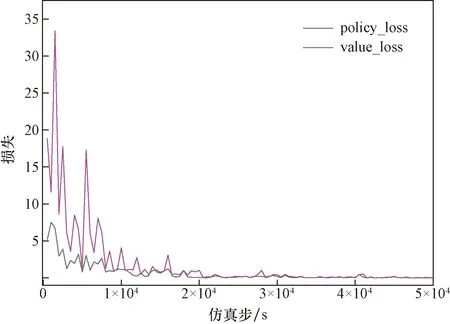
圖9 基于A2C算法的控制模型值函數與策略函數損失值Fig.9 Loss of control model value function and strategy function based on A2C algorithm

將訓練好的交叉口信號控制模型進行測試,以單位時間內(每分鐘)交叉口檢測區域內的總停駛車輛數以及交叉口各進口道總車輛延誤為判定指標,評價各控制方案的優劣性,結果如圖10所示。

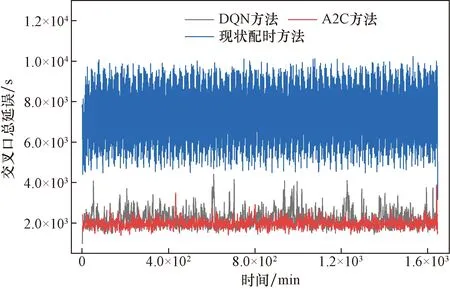
圖10 各控制方案效果對比(以交叉口總延誤為指標)Fig.10 Effect comparison of control schemes (with total delay at intersection as index)

本文所構建的模型所產生的行駛延誤較小,相比于現狀基礎配時延誤降低約65.7%,相比于DQN算法控制模型交叉口總延誤降低約21.4%。

為進一步對比本文模型相比于DQN算法控制模型的性能,將仿真過程中檢測器收集的交叉口總延誤數據以及每分鐘交叉口各進口道的停駛車輛數在時間步上進行差值處理,結果如圖11和圖12所示,大部分仿真時間內基于A2C所構建的信號控制模型在單位時間產生的延誤大小以及停駛車輛數均低于基于DQN算法所構建的信號控制模型,從仿真實驗結果數據中將公交車的運行數據進行處理,如圖13所示,所有實驗組中,本文模型的公交車平均停車次數以及排隊等待時間最低,從而驗證了本文模型的有效性。

圖11 交叉口總延誤差值處理情況Fig.11 Processing of total delay difference at intersection

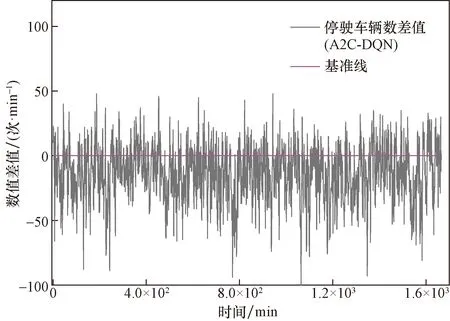
圖12 交叉口停駛車輛數差值處理情況Fig.12 Treatment of difference of stopped vehicles at the intersection

圖13 公交車運行指標效果對比Fig.13 Comparison of bus operation indicators

4 結論

研究了以考慮大型活動進行為背景的關鍵交叉口信號控制方法,在構建模型的過程中充分考慮并分析大型活動周邊道路的交通流運行規律以及大型活動參與者的出行特征,將以傳統深度強化學習為基礎的信號控制方法中的控制指標更改為以單位時間內交叉口停駛車輛數為主,不同出行方式平均時間損失以及總延誤時間為輔的形式,不僅優化了交叉口的綠燈使用效率,提高了交叉口的運行質量,同時降低了公共交通的出行延誤,在一定程度上為大型活動的順利舉辦提供了一定的有效措施。仿真實驗表明,本文所構建的以深度強化學習方法A2C為基礎,考慮大型活動出行特征的方法能有效提高交叉口的運行效率,同時降低了公共交通的延誤,有效緩解交通擁堵現象。

但是目前的研究內容僅針對活動場館的單交叉口,對于活動舉辦場館周邊的多個關鍵交叉口的信號協調控制問題,是后續研究的方向。