一道橢圓數量積為定值問題的解法探究及推廣

貴州省普定縣第一中學 (562100) 姚登美

貴州省六盤水市第二中學 (553401) 張 東

一、試題呈現

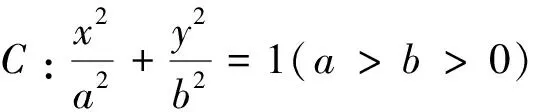
圖1

(1)求C的方程;

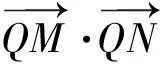
評析:試題改編于數學教材中的一道課后習題,試題以向量為背景設置數學問題情境,引導學生重視教材習題,學會知識遷移;第(1)問考查橢圓的基本概念、基本性質,借助數形結合易求出橢圓C的方程.第(2)問考查圓錐曲線中的定值、定點問題,試題從向量數量積的視角立意命題,聚焦學生對圓錐曲線中的數學思想、解題方法的理解和應用,綜合考查了學生邏輯推理、幾何直觀、數學運算的能力素養.

二、解法探究

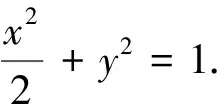
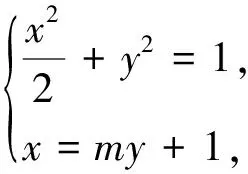
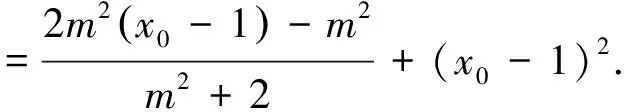
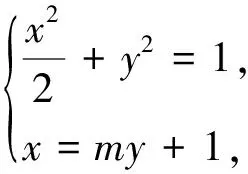
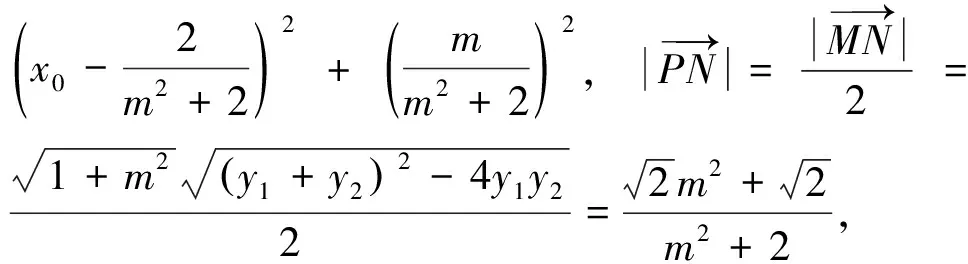
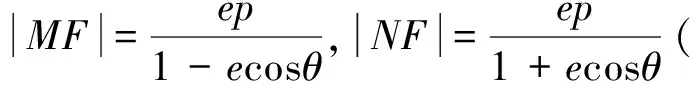
評注：向量是集“形”和“數”融為一體的數學運算工具,借助向量運算可以處理許多圓錐曲線問題,上述解法從向量數量積的幾何形式和代數形式給出了解答,綜合比較上述解法,點乘雙根法易于簡化運算、探究推廣.用多種方法解答同一道數學題,不僅能更牢固地掌握相關知識,還能更靈活地運用所學知識.通過一題多解,分析、比較各種解法,可以找到最佳的解題路徑,從而發散學生思維能力,對鞏固知識和解題能力大有裨益,是提高數學成績的一條捷徑.

三、結論探究及推廣

考慮到直線l過的定點F為橢圓的焦點,定點F具有特殊性,上述解題方法有一定的局限性,這里我們對焦點F一般化,從橢圓方程拓展到圓錐曲線,利用點乘雙根法的運算思路,做如下探究推廣.

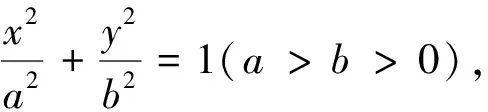
證明：設直線l的方程為x=my+n,M(x1,y1),N(x2,y2),Q(x0,y0),聯立方程組

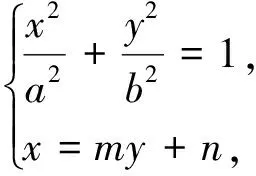
證法妨探究1,此略.

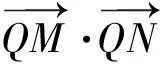
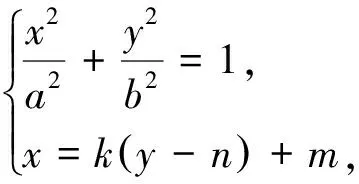
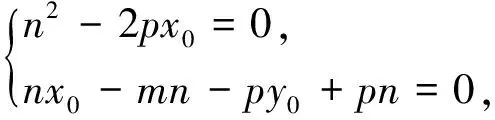
以上分別從橢圓x軸上的定點、雙曲線y軸上的定點和拋物線所在平面內的定點,對向量數量積定值問題進行了一般性探究,我們可得出圓錐曲線中向量數量積定值問題的一般性質.

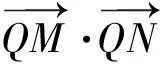
該性質的證明可類比上述探究過程得到驗證.

四、解后反思

數學教育家波利亞說過:“好的問題和某種蘑菇有點相似之處,它們都成串生長,找到一個以后,我們應該四處看看,很有可能在很近的地方又能找到更多的”.在解題教學中,教師要善于為學生創設數學問題情境,讓學生學會在數學情境中發現問題、分析問題,而不是為了解題而解題,搞題海戰術、大量刷題.在獲得問題答案后,我們應引導學生對問題答案類比分析、歸納重組,挖掘數學問題背后隱含的一般性數學規律,更加清晰地看清數學問題的本質.讓學生養成多角度、多層次思考問題和解決問題的思維習慣,形成概括歸納、演繹推理、辯證批判的能力素養,學生才能從機械刷題、題海戰術中解放出來.