探索二元不等式約束條件下函數最值的求解

山東省寧陽縣復圣中學 (271400) 張志剛

二元方程條件下的最值問題歷來是高考、競賽、高校強基計劃測試等考查的熱點,近三年高考就有2020年新高考全國I卷第11題、新高考全國II卷第12題、天津卷第14題、江蘇卷第12題,2022年新高考全國II卷第12題等,自然也吸引了眾多數學教育工作者對此深入探討,形成了日益成熟的解題理論(參見文[1][2]等).然而,此類試題的命題模式多年來鮮有變化,似有陷于僵化之嫌.如何改變問題呈現樣態,減少考試固化給機械訓練和大量刷題帶來的收益,同時強化其選拔功能呢?下面的兩道高校選拔試題將條件由方程變更為不等式,使傳統的二元函數最值問題煥發出新的生機,代表了試題改革的一個新趨向,具有較高的研究價值.

1 案例呈現

兩例均考查不等式約束條件下二元函數的最值問題,情境相對新穎,思維跨度更大,呈現出更強的綜合性與選拔性.

2 案例解答

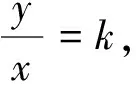
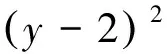
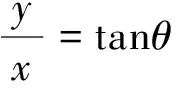
評注：通過換元轉化為二次方程有解,利用判別式Δ≥0構造不等式,也是處理二元函數最值問題的常見思路.

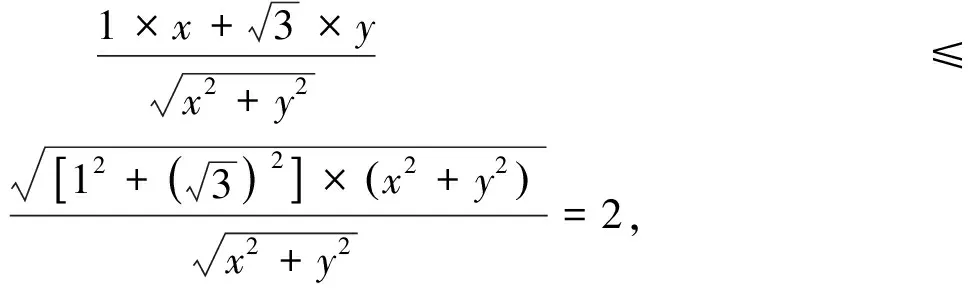
評注：柯西不等式是探求函數(特別是多元函數)最值的有力工具.解法4通過柯西不等式放縮一次性消除變元x,y,使代數式轉化為常數2(即所求最大值),體現了消元思想.在利用柯西不等式解題時,往往借助拆項、添項、配湊等技巧,以構造出柯西不等式的結構形式.此外,要驗證等號能否成立.

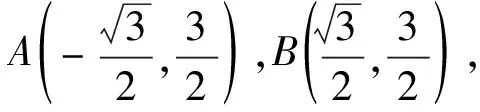
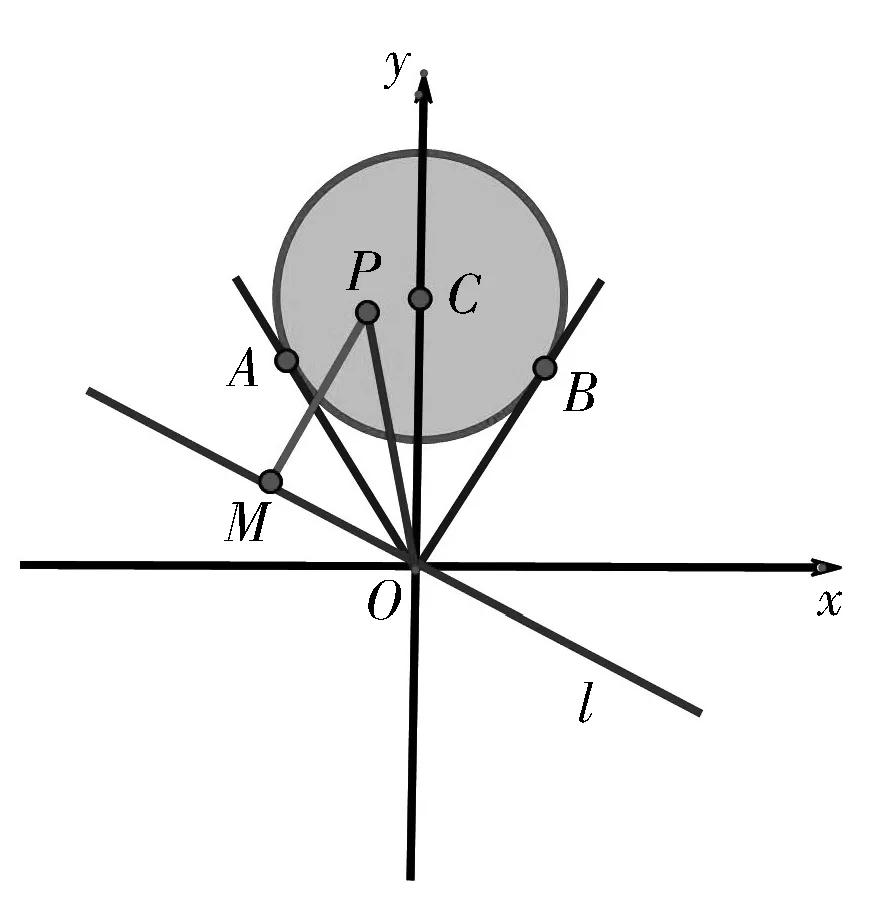
圖1

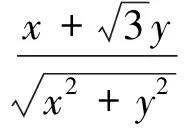
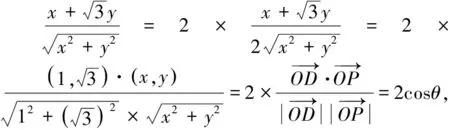
評注：本解法在解法5解析式變形基礎上繼續配湊為兩個向量的夾角公式形式,轉化為兩個向量夾角的余弦函數最值問題.

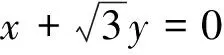
3 強化訓練

近年,不等式條件下的最值試題頻頻出現于高校強基計劃測試等選拔性考試中,代表了二元函數最值問題命題的一個新趨向,成為一道靚麗的風景線.下面再舉幾例.

例1 (2020年清華大學強基計劃測試第1題)已知x2+y2≤1,則x2+xy-y2的取值范圍為( ).

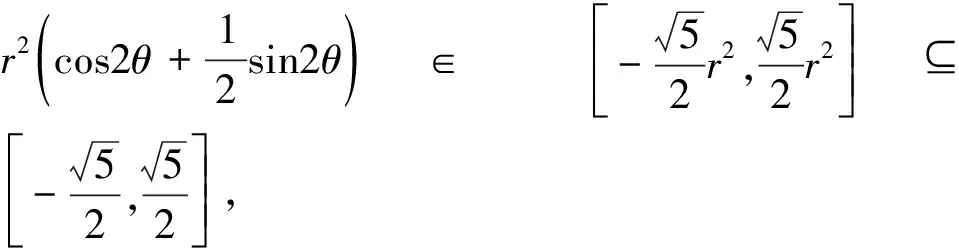
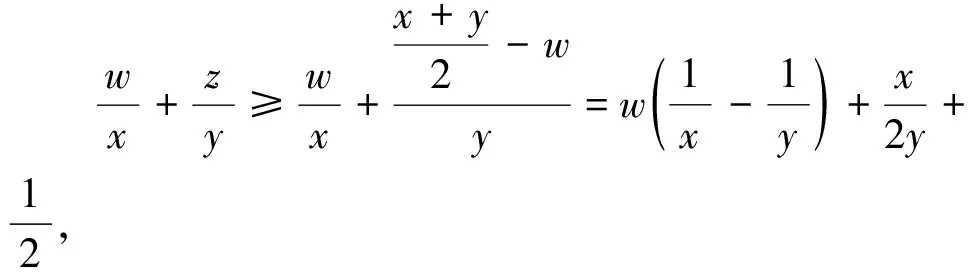
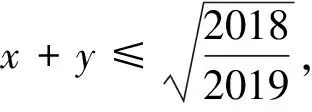
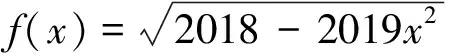
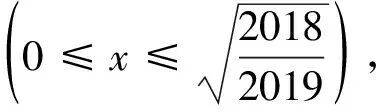
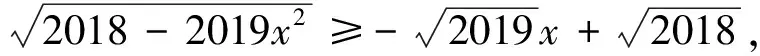
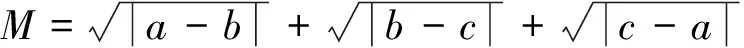
4 結語

在教學和命題實踐中,通過情境設置考查學生的關鍵能力和核心素養,是當前中、高考改革以及國際考試測量的基本方向.高考命題一方面將進一步創新試題的情境創設和呈現方式,另一方面將進一步加大試題的開放性和探究性,實現對學生創新思維和批判性思維的考查.可見,高考評價體系引領下的命題情境將進一步呈現復雜性、綜合性和創新型的特點.二元不等式條件下的最值問題通過創新問題情境,區分度更高,能有效驅動學生與情境之間持續而有意義的互動,促進學生積極剖析條件,捕捉信息,抓住關鍵,形成設想,構建方案,將所學知識遷移到新情境,解決新問題,與高考評價體系的要求相契合.