整體設計 尋求“通法” 關聯(lián)本質(zhì)
——『小數(shù)乘除法的復習』教學實踐與思考

文 莊麗君

小數(shù)乘法、除法運算類型不同，但算法相通，學法相近。復習時溝通兩個板塊的算法、學法，系統(tǒng)整理其中的計算方法和計算道理，有利于學生從整體上把握知識結構，形成轉化思想，感受計算的一致性，發(fā)展學生的數(shù)學思維。

一、課前思考

“小數(shù)乘除法的復習”是人教版五年級上冊第一單元“小數(shù)乘法”、第三單元“小數(shù)除法”的教學內(nèi)容。按常見教材編排方式，往往是一單元一復習，教材卻打破常規(guī)，將兩個單元放在一起復習，這樣編排，絕不是單純的量的累積。那么，這兩個單元內(nèi)容之間有著怎樣的聯(lián)系？又該如何組織教學展開復習，幫助學生理清聯(lián)系和建構知識呢？

1.抓住小數(shù)乘法與小數(shù)除法算法相通之處，體現(xiàn)知識結構的整體性。

橫向?qū)Ρ取靶?shù)乘法”和“小數(shù)除法”兩個單元，兩者學習內(nèi)容顯然不同，但它們的算法和學法都有相通之處，都是轉化成整數(shù)乘除法來進行計算，再運用乘除法的運算規(guī)律處理積或商的小數(shù)點位置。

復習時，可以有意識地抓住這一相通之處做文章，合理選用素材，設計題組練習，整體推進教學。教材以9 道一般的小數(shù)乘除法習題為素材，要求學生先計算，再給出整理要點對知識進行梳理。我們對習題素材加以改變，以題組方式呈現(xiàn)，如326×14 和3.26×1.4，798÷57 和7.98÷0.57，這樣的題組對比性很強，練習指向明確，學生通過觀察、計算，能主動發(fā)現(xiàn)題組的數(shù)據(jù)特點，快速捕捉到小數(shù)乘法與除法在算法上的共性———“轉化”，從而引導學生整體系統(tǒng)地整理小數(shù)乘除法的計算內(nèi)容，總結轉化的數(shù)學思想方法，使知識和思想方法都得以結構化。

2.溝通整數(shù)乘除法與小數(shù)乘除法的內(nèi)在聯(lián)系，體會運算本質(zhì)的一致性。

縱向思考整數(shù)乘除法和小數(shù)乘除法的關系，前者為后者算理算法的遷移學習提供了重要基礎，后者是前者的延伸和拓展。從整數(shù)運算到小數(shù)運算，僅僅是數(shù)范疇的變化嗎？在這個過程中，計數(shù)單位進行了擴充，運算意義也得以拓展。這時，如果能抓住這一關鍵聯(lián)接點有效設計教學，學生就能從根本上體會到乘除法運算的本質(zhì)就是計數(shù)單位的疊加和細分。

其實，從整數(shù)乘除法跨越到小數(shù)乘除法，很多變化學生是有直觀感受的。比如低年級時，10÷3=3……1，學生對有余數(shù)的除法已經(jīng)熟練掌握，學習小數(shù)除法后，原來不能再除的可以繼續(xù)除下去了，原來得數(shù)是3……1，現(xiàn)在變成了3.3˙，這是一個非常直觀的視覺沖擊。有這樣的變化其根本原因為何？因為數(shù)的領域從整數(shù)擴展到了小數(shù)，計數(shù)單位進行了擴充，1 個一就可以繼續(xù)細分轉化為10個十分之一，計數(shù)單位化小，個數(shù)增多，得以實現(xiàn)再一次的平均分，所以表象看似不同，但本質(zhì)指向一致。抓住這一關鍵變化，恰恰是打通整數(shù)除法與小數(shù)除法知識脈絡，讓學生體會運算本質(zhì)的一致性的絕佳時機。教學時，可以設計一個開放式的問題，啟迪學生深度思考——在小數(shù)乘除法的學習中，有沒有一個算式讓你覺得與整數(shù)乘除法比有很大差異的、很特別的或是有困惑的？讓學生寫一寫、說一說，抓住源于學生的重要素材，暴露來自學生的真實感受，通過辨析討論，深度挖掘表象背后的根本原因，直擊數(shù)學本質(zhì)。

二、教學實踐

（一）巧設計，找共性，梳理知識結構，感悟轉化思想

1.對比練習，梳理知識。

學生完成題組練習：326×14，3.26×1.4，798÷57，7.98÷0.57。

（1）反饋普通筆算方法，校對答案。

（2）反饋利用推算得出得數(shù)的方法，引發(fā)思考。

師：（選取學生作品展示）觀察這位同學的做法，你想說什么？

生：他先筆算第一題乘法，第二題不用筆算，只要添小數(shù)點就行了。第三題算完后，第四題也是這樣處理。

師：看來小數(shù)乘除法與整數(shù)乘除法之間有著緊密聯(lián)系。接下去小組合作理一理：小數(shù)乘法、除法分別是怎樣計算的？它們與整數(shù)乘法、除法有什么相同點和不同點呢？

小組交流，全班匯報，師生一起梳理小數(shù)乘除法的計算法則。

2.啟迪思考，溝通聯(lián)系。

師：明明是小數(shù)乘除法，為什么可以想成整數(shù)乘除法去算呢？

生：我們學過積的變化規(guī)律，知道因數(shù)如果擴大或縮小，積也會跟著擴大或縮小相同的倍數(shù)。把3.26×1.4 想成326×14，積就擴大了1000 倍，所以算出得數(shù)后，要縮小到原來的

生：小數(shù)除法是根據(jù)商不變性質(zhì)，被除數(shù)和除數(shù)同時擴大或縮小相同的倍數(shù)，商不變。所以7.98÷0.57 想成798÷57，商是一樣的。

小結：我們在學習小數(shù)乘除法時，都是想到了把它們轉化成學過的知識，分別依據(jù)積的變化規(guī)律、商不變的性質(zhì)轉化成整數(shù)乘除法去算，同時我們還運用這些規(guī)律來處理得數(shù)小數(shù)點的位置。

【思考：筆算習題以題組方式呈現(xiàn)，學生能快速捕捉到數(shù)據(jù)特點，但礙于日常做題習慣，大部分學生會題題筆算，但個別學生就會“偷個懶”，第二、四題會省略筆算過程。教學時抓住這樣的作品，讓學生對比觀察，有學生表示自己筆算時其實也是這樣思考的，有學生會質(zhì)疑這樣答題“格式”不對，正是這樣的強烈對比和矛盾沖突才更能直接切中主題，使學生快速地將思考火力集中到“小數(shù)乘法、除法分別是怎樣計算的？為什么可以這樣算？”并能夠從整體的視角對兩個單元的計算內(nèi)容進行結構化的梳理和總結。】

（二）引深思，抓特性，分析背后原因，凸顯運算本質(zhì)

1.提出要求。

師：在小數(shù)乘除法的學習中，有沒有一個算式讓你覺得與整數(shù)乘除法有很大差異的、很特別的或是有困惑的？寫一寫，并說一說你的想法。

2.分組呈現(xiàn)作品，學生介紹想法。

生1：3÷8=0.375，原來3÷8 不夠除了，學了小數(shù)乘除法后，較小的數(shù)也可以除以較大的數(shù)了。

生2：10÷3=3.3˙，整數(shù)乘除法中除后有余數(shù)，學了小數(shù)乘除法后余數(shù)可以繼續(xù)除，商還可以是循環(huán)小數(shù)。

師：10÷3=3……1，余數(shù)1 其實和3÷8 一樣，原來在整數(shù)除法中不夠除了，但學了小數(shù)除法后，還能繼續(xù)除。這是為什么？

生：個位上余下的1 可以化成10 個十分之一繼續(xù)除，如果還有余數(shù)再化為幾個百分之一繼續(xù)除，可以不斷除下去，結果可能是有限小數(shù)，也可能是無限小數(shù)。

小結：小數(shù)除法和整數(shù)除法一樣，都是把計數(shù)單位不斷地轉化、細分。

生1：9×0.1=0.9，整數(shù)乘法中，積常常越乘越大，小數(shù)乘法卻越乘越小。

生2：8÷0.1=80，小數(shù)除法卻相反，以前商越除越小，現(xiàn)在商越除越大。

師：你能說說這背后的原因或藏著的規(guī)律嗎？

生：一個數(shù)（0 除外）乘比1 小的數(shù)，積比原數(shù)小，乘比1 大的數(shù)，積比原數(shù)大；一個數(shù)除以比1小的數(shù)（0 除外），商比原數(shù)大……

小結：小數(shù)乘除法有著自己的運算規(guī)律和特點。

生：4.2÷0.25，可以用商不變性質(zhì)變成（4.2×4）÷（0.25×4），轉化成除數(shù)是1 的除法算式，這樣方便計算。

小結：利用小數(shù)乘除法與整數(shù)乘除法的聯(lián)系，有時也能幫助我們巧算速算。

【思考：要求學生寫一個小數(shù)乘除法與整數(shù)乘除法相比有較大差異的算式，由于問題有一定的自主性和開放性，學生很樂于表達，呈現(xiàn)的素材豐富而又真實，也正因為是自己所寫，反饋時，學生說和聽的興趣都很濃厚。不同的算式分組反饋，可以對兩個單元中有關運算意義、運算規(guī)律、簡便運算等知識進行有條理的回顧和梳理，達到復習的效果。其中第一組算式是深刻理解運算本質(zhì)一致性的重要素材，可以重點反饋，抓住學生“從整數(shù)除法中算到個位就結束，到小數(shù)除法中可以繼續(xù)除”的直觀感受，深究其中緣由，通過回顧學習過程，深度辨析討論，感受計數(shù)單位的擴充連帶著運算意義的拓展，使學生能站在乘除法計算大領域的高度去重新審讀這些知識，把前后關聯(lián)的兩塊計算內(nèi)容融為一體，初步體會數(shù)與運算的一致性。】

（三）優(yōu)算法，重推理，培養(yǎng)運算能力，發(fā)展數(shù)學思維

作為計算類復習課，練習設計除了關注學生知識、技能的掌握度，更要關注學生運算能力的提升和數(shù)學思維的發(fā)展。

課中設計了這樣一組習題：

【思考：練習要求為“計算”，而不是明確要求“用豎式計算”“能簡便的要簡便”。這樣設計，一方面是考查筆算的掌握度；另一方面希望在算法上不限制學生，考查計算方法的靈活性。】

比如6÷0.25，學生出現(xiàn)了兩種方法：

方法1：

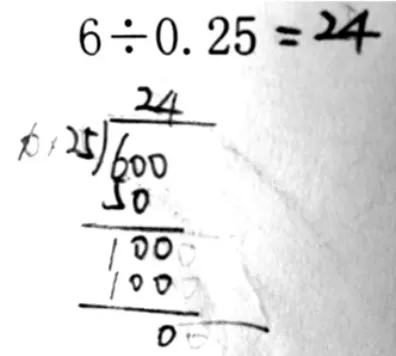
方法2：

兩種方法都能得出結果，但思維水平卻不同，前者是常規(guī)筆算，后者卻能自覺運用性質(zhì)進行簡算。

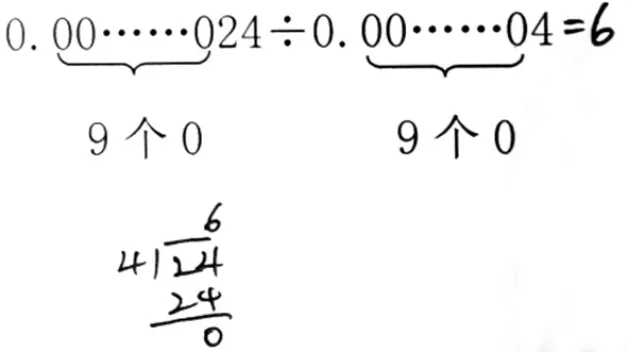
再比如最后一題，學生方法不盡相同，但都想到了運用“轉化”的思想方法。

方法1：

方法2：

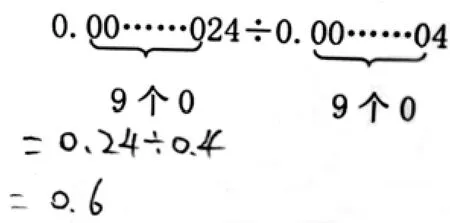
兩種方法各有近半數(shù)學生，但在計算方法的深刻性上呈現(xiàn)出了一定差異。方法2 更善于從繁雜的表面現(xiàn)象中，抓住事物的本質(zhì)和核心———即“將除數(shù)是小數(shù)的除法轉化成除數(shù)是整數(shù)的除法”，并能正確移動小數(shù)點得出正確結果。

整節(jié)課將兩個單元的復習內(nèi)容合二為一，復習的量看似增加，但基于整合的視角巧妙地設計教學活動，突出復習重點，深化復習目標，更整體地溝通小數(shù)乘除法與整數(shù)乘除法的內(nèi)在聯(lián)系，使學生建立系統(tǒng)的知識結構；更鮮明地體現(xiàn)將未知轉化為已知的學習過程，使學生形成轉化的思想方法；更深刻地感悟乘除法的本質(zhì)是計數(shù)單位的疊加和細分，使學生體會運算本質(zhì)的一致性。