基于計數單位感悟運算一致性
——《分數除以整數》素養進階習題展評與教學建議
文|鮑莉麗
一、習題展評
●習題一
1.習題內容
算一算,想一想這么算的道理是什么,連一連。
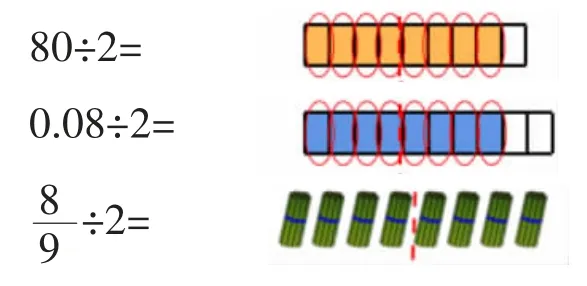
結合算的過程,它們都可以轉化為()÷()來計算。
2.能力指向
主要指向運算能力和推理意識。本題的運算能力表現為以下兩點:一是如何算,即對算法與運算程序的運用,表現為運算的熟練性;二是“為什么可以這么算”,即對算理的理解。而推理意識表現為對運算一致性的理解,基于計數單位合乎邏輯地運用運算的定義及算理感悟到都是把計數單位的個數平均分。
3.學情分析
本題的正確率達到82.5%,大部分學生能發現這三道計算題都能轉化為“8÷2”來計算。說明學生對計算都比較熟練,而且知道計算道理,并能感悟到整數除法、小數除法和分數除以整數之間的運算一致性。
●習題二
1.習題內容


2.能力指向
主要指向運算能力和推理意識。表現為對算法算理的理解,能夠根據運算律、運算法則和運算程序進行運算和推理,并理解運算對象、運算律與算法之間的關系,感悟運算的一致性。本題考查分數除以整數,通過對算法算理的理解,發現當分子能被整數整除和不能被整除兩種情況都能夠從計數單位角度進行分析,感悟把計數單位個數平均分和計數單位平均分的一致性。
3.學情分析
對于分子除以整數,多數學生能通過文字、圖示、算式表述出是把計數單位的個數平均分的算理。但是對于分子不能被整數整除的,學生對于平均分計數單位的個數遇到了一定困難,雖然也會畫圖,但多是從分數乘法結合圖示去分析道理,沒有從計數單位平均分的角度分析。對兩種類型運算一致性的不確定,導致算法算理的割裂。
●習題三
1.習題內容
(1)算一算

(2)算一算

2.能力指向
主要指向運算能力和推理意識。表現為理解運算對象,探究運算思路,選擇運算方法,設計運算程序,求得運算結果。能夠借助分子除以整數中的計數單位經驗,遷移應用到分數除以分數,將未知轉化為已知,培養學生的遷移推理能力。
3.學情分析
二、教學建議
1.激活整數、小數除法“均分計數單位個數”經驗,體會除法運算一致性
通過回顧整數、小數除法的算法算理,激活學生“均分計數單位個數”的經驗,初步感受運算一致性。例如,可以通過對比整數、小數除法的計算方法和計算道理,總結出都可以通過計數單位來表明算理。從而猜想分數除以整數是不是也有這樣的一致性呢?通過對比引發遷移和推理,在猜想中直奔本課主題,初步體會到遷移、類比在數學學習中的重要作用,初步感受運算一致性,體會理法相融,讓后續從計數單位角度來探究有“法”可依。
2.溝通“個數均分”和“計數單位均分”的內在聯系,經歷算法之間一致性過程
分數除以整數主要有兩種方法:一種是分子除以整數,一種是乘整數的倒數。由于這兩種方法相差較大,學生在理解“一致性”的過程中出現了困難,只有溝通兩種方法之間的內在關聯,才能更進一步體會分數除以整數的一致性。例如,若用分子4÷2,分母不變得到的算法,它的道理是把4 個計數單位平均分。若用乘整數的倒數的算法,結合圖示其實就是把原來的計數單位均分了,得到了新的計數單位最后得到4 個。所以乘整數的倒數的算法若從計數單位的角度,即把計數單位均分。通過“個數均分”和“計數單位均分”的內在關聯,經歷算法之間的一致性。
3.經歷分數除以整數算法遷移,探索同分母分數、異分母分數除法一致性
通過分數除以整數,積累從計數單位探究算理算法的經驗,再將該經驗遷移運用到分數除以分數中,感悟運算一致性。例如從分子能整除,到分子不能整除,在這個過程中“均分計數單位(個數)”經驗的遷移運用。再到同分母分數相除)時,強化學生的推理過程,抓住計數單位說理,遷移運用到異分母分數相除,感悟分數除法的運算一致性。

