水下仿生撲翼機器人的發展現狀綜述

曹 勇，曹永輝，黃橋高，屈毅林，潘 光

（1.西北工業大學 航海學院，陜西 西安 710072；2.西北工業大學寧波研究院 無人航行技術研究中心，浙江 寧波 315048）

1 撲翼式魚類的生物學研究

1.1 生物原型分析

海洋覆蓋著地球表面的71%，據不完全統計，海洋中的魚類超過1.2萬種。LINDSEY[1]根據不同推進部位將魚類推進模式分為2大類：身體或尾鰭推進（Body and/or Caudal Fin propulsion，BCF）、中央鰭或對鰭推進（Media and/or Paired Fin propulsion，MPF）。根據已有的生物學信息可知：自然界中85%的魚類以BCF模式游動。基于BCF模式游動具有快速性、高效性，同時，存在著穩定性不佳、低速時效率較低等缺點。基于MPF模式游動的魚類由成對的胸鰭、背鰭、臀鰭的拍動或波動產生推力。近年來，基于MPF模式游動的魚類以其優異的機動性和穩定性逐漸受到科研工作者的關注。

蝠鲼，又被稱為魔鬼魚，是一種典型的基于MPF模式游動的魚類，屬于脊索動物門、軟骨魚綱、燕魟目、蝠鲼科、蝠鲼屬；其頭側有一對向前突出的由胸鰭分化的頭鰭，胸鰭呈翼狀，尾細且具尾刺。蝠鲼的身體部分扁平，呈菱形，具有一對尺寸較大而且運動較為靈活的近三角形的胸鰭[2]。蝠鲼在運動過程中，胸鰭基部變形較小，而胸鰭遠端因為不受身體的約束，會產生較大的變形，這種柔性變形是其推力產生的主要來源。蝠鲼的運動效率較大程度上依賴于胸鰭的柔性變形[3]。蝠鲼在游動時，僅需拍動胸鰭即可實現矢量推進的效果，蝠鲼擁有如此高超的巡游能力離不開其獨特的運動系統[4-11]。蝠鲼除了具有高效的巡游能力之外，還具有較高的機動性，其具體表現為：低速巡游過程中的快速轉彎、高速巡游過程中的懸停以及懸停過程中的原地翻轉等[12]。

KLAUSEWITZ等[2]通過對蝠鲼整體構造的研究與分析，得到了蝠鲼整體的外形比例等參數。將蝠鲼的最大展長定義為L，魚體部分的展長為0.3L，單側胸鰭的最大展長為0.35L。蝠鲼的俯視圖近似于菱形，胸鰭左右對稱，后緣端部有一凸起的垂直尾鰭，尾鰭后有數倍于體長的拖尾。在不考慮拖尾情況下，展長約為體長的2倍。最大展長方向與弦長方向交點處距蝠鲼頭部距離為0.3L，距蝠鲼尾部距離為0.2L。KLAUSEWITZ將蝠鲼的胸鰭結構沿展向分為3部分，與身體相鄰的1/3胸鰭結構稱為基行（Basal row），靠近鰭尖的1/3胸鰭結構稱為遠行（Distal row）。

圖1中給出了蝠鲼游動時向下和向上拍打的完整過程[2]，由此可以進一步看出蝠鲼胸鰭具有較好的柔性，在運動過程中會產生復雜的變形。

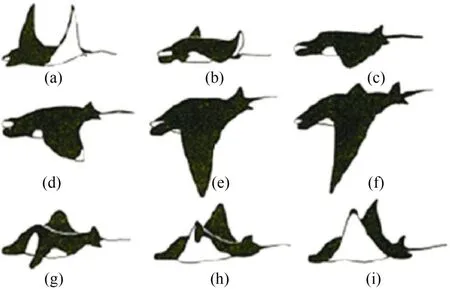
圖1 蝠鲼運動說明Fig.1 Illustration of manta ray locomotion

1.2 生物結構研究

1973年，WEBB等[13]根據胸鰭所產生的無量綱波數W=BL/λ（其中BL代表體長，λ代表胸鰭弦向的行波波長）對魚類的游動模態進行了劃分：行波數大于1為波動模態、行波數小于0.5為擺動模態。1992年，HEINE等[14-15]測量并研究了真實牛鼻鲼運動時的姿態數據。通過分析其運動模態，HEINE發現：由于牛鼻鲼寬大的柔性胸鰭與身體完全相連接，使得胸鰭難以做出前后旋轉的動作，因此需要通過胸鰭的主動變形與鰭在流場中的被動變形來適應不同的游動場景。1994年，GIBB等[16]通過解剖的方式研究了胸鰭的膜以及胸鰭內部骨架的彈性，并指出了胸鰭以及魚體與流場相互作用的復雜性，同時說明了胸鰭的運動可以分解為：繞平行于身體軸線旋轉的升沉運動及繞展向軸線旋轉的俯仰運動。1996年，ARREOLA等[17]分析了條紋毛刺魚的游動行為。發現在魚的游動過程中，胸鰭總是異相拍動。2000年，ROSENBERGER[18]指出蝠鲼肌肉動作的基本單元是其肌肉細胞。其肌肉細胞在受到來自神經系統發出的刺激信號后，會立即作出應激收縮反應，縮短并變粗，在收縮反應后，肌肉細胞又快速恢復原狀。蝠鲼胸鰭的肌肉與其橈骨之間存在聯結，在其受到神經系統的刺激后，肌肉的收縮反應會帶動相鄰橈骨的運動，進而帶動胸鰭鰭條產生變形運動。2001年，ROSENBERGER[19]對外形與鰩魚類似的多種魚類的推進模式進行研究，并發現：包括黃貂魚在內的大多數都嚴格基于胸鰭運動，少數魚類如鋸鰩等嚴格地基于身體軸向擺動運動，另外，也存在像吉他魚等在運動中將2種方式相結合。2005年，SCHAEFER等[5]通過研究典型MPF模式魚類的肌肉類型、胸鰭骨架，發現胸鰭推進模式魚類的胸鰭骨架有一定相似性，鰭骨沿展向呈放射狀，沿弦向依次排列，靠近頭部和翼根的部分鈣化嚴重，剛性更強；鰭骨之間通過聯結產生交叉支撐（cross-bracing），在形成支撐的同時便于胸鰭進行靈活變形以及波動傳遞，如圖2所示[5]。2011年，CURET等[20]研究了蝠鲼胸鰭推進魚類的外形、肌肉和骨骼分布，指出鰭條沿展向平行排列，每根鰭條在肌肉的作用下可繞著鰭根轉動，且胸鰭具有交叉支撐結構。鈣化的硬骨和軟骨組成的放射性鰭條遍布蝠鲼胸鰭的內部，每根軟骨鰭條由多段橈骨組成，可以繞關節小幅度轉動，故在展向保持一定柔性。同時，相鄰鰭條間依然存在交錯式分布的聯結，因此整個胸鰭面又表現出適度的剛性。2015年，RUSSO等[21]通過對胸鰭骨骼結締組織的拉伸測試研究了牛鼻鲼和大西洋鰩胸鰭的柔性分布，同時提出了一種生物力學模型。該模型可以復現自然界中觀察到的蝙蝠狀骨骼結構的運動特性，還研究了骨骼結構變化對胸鰭變形特性的影響。2018年，SALAZAR等[22]通過對比黃貂魚和蝠鲼的骨骼結構（如圖3所示[22]），發現黃貂魚胸鰭骨骼結構中的網狀支撐部分更靠近身體內側，撲翼邊緣的骨骼較為獨立分明；而蝠鲼的骨骼幾乎都是交叉支撐結構。這種差異決定了黃貂魚撲翼邊緣可以更為自由的波動，而蝠鲼的運動則以整個撲翼的撲動或滑翔為主。

圖2 基于MPF模式游動的魚類骨骼分布[5]Fig.2 Distribution of fish bones based on MPF mode[5]

圖3 黃貂魚和蝠鲼的骨骼結構[22]Fig.3 Skeletal structure of stingrays and manta rays[22]

基于MPF模式游動的魚類借助胸鰭和背鰭的拍動產生向前的推力，可實現6個自由度的運動、原地懸停、轉彎等。其生物學的研究成果對于水下仿生撲翼機器人的設計具有重要意義。

生物學研究的主要手段為生物的活體觀測，雖然生物的活體研究測量難度較高，產生的測量誤差較大，但活體觀測是建立生物體外形參數以及運動模型的基礎。并且可以通過對活體進行運動學和渦結構的測量來討論生物體的運動機理，以此指導仿生撲翼機器人的設計。

國內外研究團隊進行了許多機理性研究以及水下仿生撲翼機器人的研制工作。但是在計算方法、控制機構設計、機械結構設計等方面依然存在著一些亟需解決的問題。水下仿生撲翼機器人的研究還停留在模仿其生物學特性研究方面。目前，已經研制的水下仿生撲翼機器人大多是從形態上接近真實生物，而其運動特性、感知特性、驅動特性的研究還處于起始階段。

2 撲翼式魚類的動力學研究

深入理解生物游動特性有助于更好地進行仿生機器人結構優化、建立基于模型的控制策略等，對于提升機器人運動性能、實現高精度姿態控制有著至關重要的意義。針對特殊問題的理論建模分析以及具有一般性的計算流體動力學（Computational Fluid Dynamics，CFD）是研究生物游動時流場特性的常用方法[23]。

2.1 動力學模型

起初，學者們對具有“細長體”特征的魚類進行了研究并以此為基礎發展了波動推進的動力學模型，此類模型適用于無量綱波數大于0.5的波動推進魚類。LIGHTHILL[24-27]于20世紀60–70年代提出了大幅度可拉伸細長體理論（Large-Amplitude Elongated-Body Theory，LAEBT）。細長體理論將魚體簡化為由頭部至尾部的一維桿件，桿長方向記為x軸。沿x軸上某一點垂直切分得到魚體的截面Sx，位移h垂直于x軸。細長體理論假設固體周圍的流動主要由2部分組成：可拉伸細長體周圍沿游動方向的定常流動、由于細長體上某一點運動導致的非定常流動。若細長體以恒定速度U在不可壓縮流體中向前游動，則歐拉觀點下細長體周圍某一處流體質點的速度[24]為

因此截面Sx處的流體所具有的動量為ρA(x)V(x,t）。進一步地，流體質點與魚體此點之間的作用力可以通過動量的變化率[24]表示，即

將細長體上力做的功沿著弦向積分，并代入細長體的幾何假設，可以得到細長體在變形時力所做功的平均值[24]為

在不考慮能量耗散時，細長體在單位時間內對于流體做功的能量主要由2部分組成：一是保持推進速度所需要的做功，二是施加到細長體周圍流體質點的動能[24]，即

細長體單個周期產生的推力均值[24]為

式中，h(x,t)的形式對于推力均值的結果有重要的影響。因此，利用該理論進行分析時，需假定魚體或機器人運動時符合某一變形規律。

考慮佛勞德推進效率[24]：

若細長體變形規律為h(x,t) =H(x)cos(ωt)，可得到推進效率最大值不超過1/2；若考慮細長體運動時有一行波經過，即

式中，c為行波的波速，可得到推進效率為

易知細長體上行波的傳播速度與游速之比決定了推進效率。細長體理論在魚體或機器人變形已知的情況下可以給出力和效率的計算方法，使得快速求解細長體動力學問題成為可能，但LAEBT方法忽視了固體自身的變形以及流體與固體之間的耦合作用[28]。

在一維細長體理論基礎之上，WU等[29-31]發展了二維波動板理論。二維波動板將魚體或機器人視為沒有厚度的二維平面，仿生肌肉的運動變形看作平面上的行波，其維度增加至二維h（x，y，t），z為處于xoy平面上波動板垂直于平面的位移，WU討論了在這種幾何模型和運動形式下的動力學問題。CHOPRA等[32-35]通過結合Lighthill模型、機翼的有限縱橫比理論（Finite Aspect Ratio Theory）以及渦流板理論（Vortex Panel Method），將模型的應用場景提升至二維、三維，并用于新模型計算了矩形板、三角形板以及新月形魚尾的動力學問題。通過數值計算得出，當展弦比減小時，波動板產生的水動力及水動力效率將隨之減小。在CANDELIER[36-38]提供的計算案例中，將該模型與CFD計算結果進行了對比，發現兩者相差不超過10%。同時，通過將模型的計算結果與真實生物的水動力特性進行對比，發現相差不超過16%，進而證明了該模型的有效性。

另外，Cosserat桿作為軟體機器人領域常用的模型之一，考慮了結構的被動變形、幾何非線性等問題[39-41]。考慮流體作用時的LAEBT-Cosserat方法相較傳統CFD方法，計算效率得到了顯著的提升。

針對具有硬質骨骼的水下機器人撲翼的動力學建模問題，學者們一般采用基于莫里森方程的建模思路，其中基于葉素理論（Blade Element Theory）[42]推導基于MPF模式推進的仿生魚動力學模型的方法應用較為廣泛。葉素理論發展自剛性結構物旋轉場景下的動力學建模問題，如螺旋槳、機翼、飛翼機器人[43-44]等，該理論是將結構視為若干微元的組合，先通過莫里森方程求解微元體的局部力學特性，再采用積分方法求解整個結構的受力情況。

針對機器人在水下借助撲翼進行推進的問題，考慮二維胸鰭由展向或者弦向的若干微元體組成，在機器人運動過程中，將微元體視為剛體。根據莫里森方程[44]，微元體上的受力可以表示為

式中：C為水動力參數；V為微元體表面上流體質點的合速度。對微元體的受力進行積分，可以得到整個撲翼的受力情況。根據機器人的幾何特性，可以將積分方向分為垂直于流場方向、平行于流場方向、平行于仿生鰭前緣骨骼方向和垂直于仿生鰭前緣骨骼方向。

以平行于流場方向為例，考慮胸鰭展長為L的仿牛鼻鲼機器魚以速度U向前游動。此時，與翼根處距離為r的微元體的有效攻角[45]為

式中：α（r）代表此處微元體周圍流體質點合成速度與游動方向的夾角；β（r）代表此處微元體軸線方向與來流速度方向的夾角。

根據準穩態葉素理論，此時作用于微元體的升力、阻力[45]分別為

式中：ρ為流體密度；dS為微元體的面積；CLmax與CDmax為胸鰭的最大升力系數與最大阻力系數。對微元體受力沿著地面坐標系分解[45]可以得到

式中，φ為微元體與仿牛鼻鲼機器魚機體縱平面的夾角。對微元體受力的3個分量在積分方向分別積分，可以獲得胸鰭整體的受力表達式[45]

該建模方法的分析思路清晰，但將微元體視為剛體，未考慮運動過程中胸鰭的變形及流固耦合效應，且僅適用于無量綱波數較小（小于0.5）的擺動推進魚類。

以莫里森方程為基礎，通過修正模型中最大升力系數、阻力系數，可以求解不同擺動推進仿生結構的動力學問題。牛傳猛等[45]基于葉素理論計算了仿牛鼻鲼機器人胸鰭的最大升力系數和最大阻力系數，并且通過給定展弦比和最大俯仰角，推算得到了升阻力系數公式。MENG等[46]基于莫里森方程研究了具有展弦向波動運動的六自由度仿生胸鰭結構的動力學問題，數值計算結果與水動力實驗數據具有較高的一致性。WANG等[47-48]在穩準態葉素理論的基礎上，結合攻角理論分析了仿生胸鰭的動力學問題，并將游動速度的數值模擬結果與機器人實際速度對比。結果表明，在攻角10°以內兩者一致性較好。

根據無量綱波數的大小，可以將上述理論分為適用于波動推進模式（無量綱波數大于0.5）的細長體理論，以及適用于擺動推進模式（無量綱波數小于0.5）的葉素理論。通過結合不同的模型處理方法，基于這2種理論可以求解多種類型的水下推進動力學問題。但這2種理論的建模方法均需事先給定運動形式，且不考慮機器人與流體的流固耦合效應。

2.2 CFD水動力求解

隨著計算流體力學學科的逐步發展和計算機技術的不斷成熟，基于求解納維–斯托克斯方程（Navier-Stokes Equations，N-S）的數值模擬方法被廣泛應用。數值模擬方法可以獲取隨時間變化的流場細節，模擬魚類游動的真實環境，有助于研究者們理解生物游動的機理。目前數值模擬方法面臨的較大難點在于如何處理邊界運動問題，運用傳統貼體網格模擬生物游動時往往伴隨著網格畸變，極大影響了計算的效率和結果的準確性。為解決網格大變形問題，研究者們提出了幾種解決方法，如任意拉格朗日–歐拉（Arbitrary Lagrangian-Eulerian，ALE）方法、時空方法和浸沒邊界方法（Immersed Boundary Method，IBM）[49-51]。

ALE方法描述了運動參考系中的流場，最初是由HIRT等[52]在結構網格的有限差分框架中引入，SHASHKOV等[53-54]將具有有限差分框架的ALE方法推廣到任意多邊形網格中。在ALE方法中，網格伴隨著流體和固體的交界面運動，因此網格速度是N-S方程對流項中的一個參數[55]。KERN等[56]利用ALE方法研究了鰻魚型生物爆發性游動的流體動力學，得到了一些與實驗觀測結果一致的尾跡結構，定量分析了生物游動所受到的力，證明了波動型生物會根據不同的目標修改它們的運動形式；KATUMATA等[57]利用ALE法對波狀斑馬魚游動時的渦旋結構進行了詳細預測，評估了生物的水動力、功率和速度，證實渦環結構能夠促進生物游動時水動力的產生。LI等[58]基于流體–結構相互作用（Fluid-Structure Interaction，FSI）方法，分析了金槍魚類從靜止狀態到穩定巡航狀態加速過程中的游動性能和機理，對自推進行為的流體動力學進行了系統的參數研究。

時空法基于時空有限元公式，該公式已成功應用于固定空間域中的各種可壓縮和不可壓縮流動問題，其中有限元插值多項式是空間和時間的函數[55]。TEZDUYAR等[59]提出了一種變形空間域/時空方法（Deforming-Spatial-Domain/Space-Time，DSD/ST），該方法通過一種時空/時間有限元的概念來處理計算域的變形，網格隨著流體與固體的邊界一起運動。隨后該方法被陸夕云等[60]用于生物游動的數值計算中。

浸入邊界法將流場中的實體看作是N-S方程中的一個動量強迫項，并非一個真實的實體。由于浸沒邊界法的網格運動通常不遵循浸沒體的邊界，因此選擇滿足浸沒體上無滑移條件的精確插值方案至關重要[55]。這種方法最早由PESKIN[61]在1972年提出，并將其用于模擬心臟瓣膜的運動，后來被廣泛應用在具有大變形的生物流場求解當中。傳統的IBM方法采用一種數值虛構的方法模擬邊界對流體分布力的作用，采用歐拉變量描述流場的物理量，拉格朗日變量描述邊界運動產生的物理量，用Delta函數通過分布節點力和插值速度來表示流場和浸入邊界的數值交互。由于浸沒邊界法的流場在正交的笛卡爾網格中進行計算，避免了貼體網格的生成，從而有效避免了網格畸變問題，非常適用于生物游動的流場計算。

但傳統的IBM方法也存在很多缺點，如無滑移條件無法嚴格滿足、速度穿透問題、邊界不精確等。因此在隨后的研究中，各種改進的IBM方法不斷出現。MITTAL等[62]提出了一種精確邊界的浸入邊界方法來模擬復雜的三維變形問題，該方法基于離散力格式，采用鬼點策略來滿足精確的速度和壓力邊界條件，通過對魚的胸鰭運動以及蜻蜓飛行的模擬表明該方法具有較高的求解效率以及計算精度。DONG等[63]利用這種方法模擬了藍鰓太陽魚在穩定向前運動過程中的流場情況，定量表征了胸鰭的推進性能，詳細分析了推力產生的機制，以及推力與渦旋動力學的聯系。仿真結果表明，采用主動和被動鰭變形驅動是生物具有較高的推進性能的重要原因。HAN等[64]采用基于浸沒邊界法的不可壓縮N-S流動求解器，在平穩的笛卡爾網格上模擬了背/臀鰭在中鰭相互作用（Median Fin Interactions，MFI）推進中的水動力影響。模擬中發現，由于后體渦旋（Posterior Body Vortices，PBVs）與尾鰭前緣渦旋（Leading Edge Vortices，LEVs）的碰撞，后者得到了增強，同時尾鰭的推力和效率也分別提高了25.6%和29.2%。研究表明增加背/臀鰭面積會導致更強的LEVs，改變背/臀鰭撲動的時間段會影響PBVs與LEVs的碰撞時間，從而改變尾鰭性能。

以上方法在求解不可壓流動時會出現速度–壓力的解耦，解耦產生的壓力泊松方程一般采用迭代的方式進行計算，這使得數值計算收斂所消耗的資源較多。為解決這個問題，YANG等[65-66]將IBM與氣體動理學格式（Gas Kinetic Scheme，GKS）結合，成功應用于不可壓流體的求解，大大提高了N-S方程的求解效率。但該方法采用顯式算法，在拉格朗日網格量較多時求解效率低下。ZHANG等[67]基于三維顯式IB-SGKS通量求解器，針對牛鼻鲼前游動過程中胸鰭大變形問題進行計算方法的改進。通過探討不同的線性方程組求解策略，以及對拉格朗日點周圍歐拉點的搜索策略進行改進，從而解決原求解器在拉格朗日網格節點數大于1 000時計算效率低下的問題。研究結果發現在斯特勞哈爾數較高時，翼尖渦的脫落是推力產生的主要原因，而前緣渦和后緣渦的脫落則對推力產生不利的影響。但在斯特勞哈爾數較低時，前緣渦的脫落會對推力產生有利的影響。

目前流行的商業軟件采用的主要是ALE方法，存在計算結果不準確、復雜運動較難實現等局限性；時空法無法對三維模型進行分析，并且在分析二維問題時消耗的計算資源較多；浸入邊界法受制于流體和固體求解器的先進性，其計算結果的可行性仍然值得商榷。同時如何將生物的主動變形和被動變形相結合也是一大研究難點。

3 水下仿生撲翼機器人的驅動與樣機研究

基于前文對MPF模式的定義，自然界中，牛鼻鲼、蝠鲼、鷹嘴鰩等的推進方式為擺動推進；黃貂魚、尼羅河魔鬼、南美刀魚等的推進方式為波動推進。相比于BCF模式，MPF模式具備更強的穩定性和機動性。隨著仿生機器魚領域研究的不斷深入，MPF模式逐漸成為仿生機器魚領域的研究熱點。國內外很多研究機構根據MPF模式的運動特點陸續開發出多款仿生機器魚。

3.1 擺動推進的仿生胸鰭結構

2008年，德國FESTO公司、EvoLogics公司與柏林科技大學3家單位合作開發了一款名為Aqua Ray的仿蝠鲼機器魚，如圖4所示[68]。該機器魚采用無刷電機驅動的水泵為2對液壓裝置提供動力，并通過線繩驅動胸鰭骨架上下撲動。該機器魚還在胸鰭結構中采用了Fin Ray結構，可以使仿生胸鰭的運動形態與真實生物更加貼合。利用位于鰭尖的單臺舵機使胸鰭產生弦向扭轉變形，從而產生推進力。同時，利用尾鰭實現上浮下潛運動。該機器魚可以實現以0.5 m/s的速度進行游動。2010年，ZHOU等人開發了一款名為RoMan-II的仿蝠鲼機器魚。該機器魚采用多個獨立電機驅動，并列兩側的胸鰭由3根獨立的柔性鰭條驅動，每根鰭條都有單獨的驅動源提供動力，機器魚的升沉運動采用類似魚鰾的給排水裝置進行控制，可實現最大0.3 m/s的水下巡游速度[2]。2016年，CHEW等人[69]研制了一款采用單鰭條驅動的仿生蝠鲼機器魚。該機器魚單側胸鰭的展長為194 mm，最大弦長為200 mm，鰭條位于仿生胸鰭的最前端，鰭面其余部分為柔性橡膠材料。通過舵機驅動單鰭條使柔性鰭面變形進而為機器魚提供推力。同時，研究人員還針對不同厚度柔性胸鰭的推進效果進行了實驗研究，發現該機器魚最快可以達到0.5 m/s的游動速度，約為體長的1.78倍[69]。

圖4 Aqua Ray仿蝠鲼機器魚[68]Fig.4 Manta ray-inspired robotic fish Aqua Ray[68]

北京航空航天大學機器人研究所的畢樹生等人自2007年起，做了大量MPF模式的仿生魚研究，研制了五代樣機（Robo Ray系列），其中，游動速度最快可以達到0.9 m/s。樣機多采用多電機帶動多鰭條的胸鰭結構形式，在運動形態和整體結構上，仿生機器人與自然界中真實蝠鲼的相似度已逐漸提高[70-78]。2011年，國防科技大學楊少波等[79]從仿生學層面系統地開展了牛鼻鲼胸鰭推進模式的研究，研究團隊基于流固耦合的方法分析了牛鼻鲼胸鰭推進時的水動力學特性，并研制了一款名為Cownose Ray的仿牛鼻鲼機器魚，如圖5所示。團隊通過樣機的航行實驗研究了不同的運動參數下潛水器的推進性能，該機器魚可以在1 Hz的撲動頻率下以0.18 m/s的速度游動[79-81]。2022年，中國科學院的喻俊志等[46，82]研制了一款后掠角可變的MPF仿蝠鲼機器魚。該機器魚展長723 mm，最大弦長381 mm，最大可以實現每秒1.07倍體長的游動速度，基于后掠角可變的胸鰭結構，該機器魚的機動性得到了大幅的提升，可實現快速的俯仰機動，其半徑為205 mm。同時，研究團隊針對該樣機提出了基于準穩態方法的動力學模型。同年，洛桑聯邦理工的SUN等[83]通過多個齒輪泵構建了柔性致動器，可產生最大約25 N·m的力矩，并在此基礎上開發了一款胸鰭推進的仿生機器魚。該樣機展長1.93 m，其撲動頻率達到了0.5 Hz，游動速度約0.29 m/s。該機器魚的驅動方式為設計工程實際中所需求的大尺度軟體機器人提供了新的研究思路。西北工業大學的曹勇等[84-89]采用單舵機驅動單根鰭條、多臺舵機驅動并聯多根鰭條、雙驅動帶動多連桿等結構方式開發了多臺仿蝠鲼機器魚，如圖6所示[84]。其研發的翼身融合水下滑翔工程樣機完成了多次湖、海試驗工作，并實現了最大1 025 m的下潛深度，是目前國內外唯一具備大深度水下工作能力的仿生潛水器。

圖5 Cownose Ray仿牛鼻鲼機器魚[79]Fig.5 Cownose ray-inspired robotic fish Cownose Ray[79]

圖6 西北工業大學仿蝠鲼機器魚[84]Fig.6 Manta ray-inspired robotic fish from Northwestern Polytechnical University[84]

根據以上列舉的研究成果，可以發現，擺動推進的仿生機器魚在航行性能以及與生物的相似程度在逐步提升，同時也逐漸從實驗室研究階段走向工程應用階段，具備較好的應用前景。擺動推進的仿生機器魚展弦比通常處于1～2之間，因此兩側胸鰭在存在推力差時，對于轉彎機動性有較為明顯的提升，尤其是在機器魚處于低速巡游情況下。但擺動推進的機器魚存在縱向穩定性差的問題，這主要是因為胸鰭撲動過程中產生的水動力是周期性變化的，這也對胸鰭驅動結構設計以及運動控制提出了新的挑戰。

3.2 波動推進的仿生胸鰭結構

HU等[90]參照“尼羅河魔鬼”（Gymnarchus Niloticus）的長條狀背鰭，開發了一款名為RoboGnilos的波動仿生鰭裝置。該樣機由并列排布的9臺舵機驅動，每臺舵機帶動獨立鰭條，鰭條間通過柔性薄膜進行連接，通過調節舵機之間的相位差可以實現柔性薄膜波動波長的調節，該裝置可以達到約0.35 m/s的游動速度。CURET等[91]參照南美刀魚的腹鰭，開發了一款名為Robotic Knifefish的仿生波動鰭裝置。該裝置由并列排布的32臺舵機驅動，由于該裝置驅動數目的增加，在運動過程中胸鰭可以產生連續性更好的行波。CURET利用DPIV方法，對裝置的波動傳遞方式差異引起的渦結構、推力以及側向力變化進行了分析。結果表明，該裝置產生的最大射流速度可達0.5 m/s、最大升力可達0.4 N。

LIU等[92]同樣參照南美刀魚的腹鰭，開發了一款可自主游動的仿生波動鰭機器魚，如圖7所示。該機器魚采用單驅動形式，在波動鰭前緣，由一臺連續轉動的電機驅動曲柄搖桿機構往復運動，并帶動柔性鰭面運動。由于該機器魚僅在前緣進行驅動，鰭面的波動呈現由前緣至后緣振幅逐漸衰減的趨勢。相較于多驅動結構的波動鰭裝置，單驅動結構由于完全依賴鰭面的被動變形，因此不會產生額外的運動消耗，在推進能耗上有大幅下降，但逐漸衰減的波動振幅也限制了機器魚推進能力的進一步提升。經測試，該機器魚可達到約0.25 m/s的游動速度[92]。LIU等人開發了一款名為KnifeBot的仿生波動鰭機器魚，該機器魚可實現最大約0.35 m/s的游動速度。該機器魚由并列排布的16臺舵機驅動，通過調節舵機相位差調節鰭面波長以及波動傳遞方向，其利用DPIV方法對該機器魚的不同波動傳遞方式進行了研究，得益于該機器魚的自主游動能力，除游動速度外，還可獲得不同波長、撲動頻率對俯仰角、橫滾角、偏航角的影響規律[93]。

圖7 仿刀魚波動鰭機器魚[92]Fig.7 Knifefish-inspired robotic fish with fluctuating fin[92]

國防科技大學與Pliant Energy Systems公司分別開發了2款可實現水陸兩棲的仿生波動鰭機器人，如圖8所示[94]。二者分別采用橡膠以及硅膠作為鰭面材料，其中，由于前者鰭面材料硬度更高，使得其可在水下、沙地、冰面以及雪地等多種地形條件下實現快速運動，后者爬行速度約為0.1 m/s，游動速度為0.3 m/s[94-95]。

圖8 水陸兩棲仿生波動鰭機器魚[94]Fig.8 Amphibious bionic robot fish with fluctuating fin[94]

根據以上列舉的研究成果，可以發現，波動推進的仿生魚逐漸脫離了仿生對象的束縛，從單波動鰭過渡到多波動鰭，并利用波動傳遞的特性，使波動鰭機器魚具備了水–陸兩棲的功能，具備較好的應用前景。波動推進的仿生機器魚展弦比通常處于小于1，且鰭面存在的無量綱波數大于1，這就使得其產生的推力是連續的，因此也具備更好的穩定性。但波動推進機器魚由于采用多個驅動裝置，且驅動裝置之間通過柔性材料連接，在運動過程中會存在運動和變形相互制約，相互影響的情況，因此功耗較高，對能源系統提出了新的挑戰。

3.3 采用軟體驅動器的胸鰭推進機器魚

軟體驅動器是指全部或部分由柔性材料制成、能夠實現連續變形的驅動器，相比于傳統剛性驅動器，其具備極高的運動自由度和極強的環境適應性，還可實現自組裝、自修復、自感知等功能，在胸鰭推進的仿生機器魚領域有巨大的應用空間。

已經研制的胸鰭推進式軟體機器魚所采用的驅動方式包括：氣動[72，96-97]、形狀記憶合金（Shape Memory Alloy，SMA）[98-100]、離子聚合物–金屬復合材料（Ionic Polymer-metal Composites，IPMC）[101-103]、介電彈性體驅動（Dielectric Elastomer Actuator，DEA）[104-105]和生物融合驅動（Bio-hybrid Actuation）[10，106]。

氣動指在軟體結構中充入氣體，通過改變氣體體積或內部壓力，使結構產生運動與變形的一種驅動方式。日本岡山大學SUZUMORI等[96]及北京航空航天大學CAI等[72]都先后研制了胸鰭推進的氣動軟體機器魚。2022年，CHI等采用氣動驅動并結合多穩態結構成功研制了胸鰭推進的蝶泳式機器魚，游動速度可達每秒3.74倍體長，是目前世界上游動最快的軟體機器魚[97]。氣動具有驅動力強、運動靈活等優勢；其發展較早且十分成熟，但通常需要外接氣源，因此不適用于無纜的自主游動。

基于SMA材料驅動器的基本原理是：通過電流、光照等方式加熱使SMA產生相變，同時產生變形。KIM等[98]研發了一種基于SMA驅動的仿生海龜。WANG等[99]設計研究了一種基于SMA驅動的擺尾機器魚和仿蝠鲼機器魚。基于SMA的驅動器具有驅動力大、變形量大等優勢；但由于其散熱較慢，驅動后較長時間才能夠恢復至初始狀態，導致驅動頻率較低。

IPMC是一種電活性聚合物材料（Electroactive Polymer，EAP）。在IPMC的電極兩端施加電壓時，水合陽離子在電場作用下移向負極，負極產生拉伸變形，同時，正極發生收縮變形，材料整體則發生彎曲變形。HUBBARD等[101]將IPMC應用于仿生機器魚胸鰭和尾鰭的驅動設計。SHEN等[102]通過模仿海豚的游動方式，使用IPMC研發了一款仿生機器魚，并研究了其水動力性能。弗吉尼亞大學的研究者[103]基于IPMC驅動研發了一款仿生蝠鲼機器魚，該機器魚的胸鰭由兩側的IPMC鰭條驅動，身長80 mm，翼展180 mm，最大游動速度為4.2 mm/s。IPMC具有變形靈活、位移大、驅動電壓低、響應速度快等優點。由于其驅動需要液體環境，因此IPMC與機器魚適配性強。但IPMC仍存在輸出力度小、響應頻率低等不足，在實現復雜運動和高效控制方面仍面臨一些挑戰。

以介電彈性體薄膜結構為例，可以對DEA的驅動原理進行簡單說明：在介電彈性體薄膜上下兩側的電極上施加電壓，介電彈性體薄膜在Maxwell應力的作用下發生變形，例如薄膜厚度減小，橫向產生擴張等。近期，LI等[104]研制了介電彈性體驅動的仿生獅子魚，完成了馬里亞納海溝的深海驅動實驗，并實現了全局視覺下軟體機器魚集群運動實驗[105]。介電彈性體驅動器具有極高的能量密度和良好的頻率響應特性，在許多領域都有著廣闊的應用前景。但由于其機理復雜，在設計仿生運動時仍有很大挑戰。

生物融合驅動指：將生物材料如動物肌肉組織作為驅動器整合到軟體機器人系統中，使其針對外界刺激（如電場、光刺激等）做出反應的一種驅動方式。2016年，PARK等[10]利用大鼠心肌細胞研制了一種生物融合驅動的黃貂魚機器人，所研制的機器人能夠通過光趨近進行導航。2022年，ZHANG等[106]成功研制了一種肌肉組織驅動的仿蝠鲼機器人，其僅由一塊肌肉組織驅動就可以實現有效推進。生物融合驅動的生物兼容性強，能對外界刺激（光信號、電場等）做出反應，但其制備困難，對環境要求高，該領域的研究目前仍處于起始階段。

除此之外，軟體驅動還包括燃燒（化學驅動）、電液壓驅動（Electrohydraulic Actuation）等驅動方式。其中，燃燒能夠在短時間內爆發大量能量，但二次驅動效果差，在彈跳機器人[107]、跨介質機器人[108]領域應用廣泛。針對軟體機器魚的設計而言，不難看出，化學驅動在快速逃逸、躍出水面等研究方向具備巨大潛力。2018年，ACOME等[109]提出的HASEL驅動器（Hydraulically Amplified Self-Healing Electrostatic Actuator，HASEL Actuator）是一類典型的電液壓驅動器，能夠實現拉伸[110]、彎曲[111]、旋轉[112]、扭轉[113]等多種運動及變形形式。其能量密度高、輸出能力強、易于快速制備，在設計具備復雜仿生運動能力的胸鰭推進軟體機器魚方面具備廣闊的前景。

根據以上所列舉的研究成果，可以看出，大部分研究工作主要關注具體軟體驅動機理，所研制的機器魚樣機運動形式單一、操控性差，難以實現復雜仿生運動。在撲翼軟體機器魚的研究過程中，還面臨著許多挑戰：例如，在驅動器層面，如何設計和研制能夠滿足胸鰭推進特性的軟體驅動器；在系統層面，如何根據魚類胸鰭運動變形特性，采用一種或多種軟體驅動方式設計具備復雜仿生運動能力的仿生胸鰭推進系統；在運動控制層面，如何根據軟體驅動器驅動特性設計運動控制系統，實現復雜仿生運動控制。總而言之，在運動效果和應用能力方面，與傳統機器魚相比，軟體機器魚仍有較大的提升空間。

4 水下仿生撲翼機器人的控制研究

本節根據水下撲翼機器人的控制目標，將水下撲翼機器人的控制研究內容分為以下幾大類：1）撲翼驅動控制；2）俯仰與深度控制；3）轉彎與航向控制；4）路徑點與路徑跟蹤；5）避障與自主游動；6）基于相似度的運動參數優化。針對以上研究內容，本節主要闡述面向不同控制任務的控制要求與難點，討論不同控制器對同一控制目標的應用特點，為水下撲翼機器人的控制器設計提供參考。

4.1 撲翼驅動控制

水下撲翼機器人的游動借助成對撲翼的拍動或波動，通過撲翼運動過程中與水的相互作用，推進自身游動。目前，撲翼驅動控制的方法要有基于運動學模型的方法、基于動力學模型的方法以及基于中央模式發生器（Central Pattern Generators，CPG）的方法等[114-118]。

針對基于運動學模型的方法，LOW等[119]利用模型的運動學方程，導出了2種形式的多鏈機器魚步態規劃的一般解，該解被用作六鏈體尾鰭式機器魚、八鏈胸鰭式機器魚游動試驗的步態控制輸入，實現了對RoMan-III兩側柔性胸鰭的驅動，實驗表明其開環游動的最大速度為0.45 m/s。WU等[120]提出了一種基于連桿機構的新型仿蝠鲼機器人，作者對連桿機構的運動學模型進行了分析，并進行了仿生機器人的水下實驗，其胸鰭的運動軌跡與蝠鲼胸鰭的運動軌跡相近。LIU等[121]對仿蝠鲼機器人進行了運動學和水動力學的仿真分析，并在水池中進行了測試，該機器人能通過改變兩側胸鰭的幅值實現簡單的橫滾和俯仰運動，從而實現游動和轉向。WANG等[122]提出了一種基于波動式胸鰭的仿蝠鲼機器人，并對波動式胸鰭的運動學模型進行了分析，實現了前后游動、俯仰、轉彎3個基本動作并進行了評價。

針對基于動力學模型的方法，CAI等[123]、MENG等[46]建立了仿生胸鰭的簡化水動力學模型，測試了所設計的胸鰭機構及仿蝠鲼機器人的運動性能，但仿真結果與實驗結果之間仍有明顯的誤差。目前，由于剛體與柔性耦合變形的水動力分析十分復雜，建立一個精確的胸鰭動力學模型是非常困難的。因此，基于動力學模型的驅動控制方法仍然較少。

基于目前的情況，更加穩定、可靠且無需節奏信號反饋的CPG方法開始被大量運用。CAI等[124-125]開展了仿蝠鲼機器魚的CPG多運動模態協調控制研究，進行胸尾鰭結構的驅動，實現了撲動前游、倒游、原地轉彎等運動姿態；ZHANG等[126]設計了一個CPG模型，實現了仿生機器魚的多模態機動運動，實驗表明利用胸尾鰭一體化推進機構，機器魚可以更穩定、更高效地進行靈活的機動游動；CAO等[123]改進了基于相位振蕩器的CPG模型，引入了空間與時間上的非對稱效應，完成了對多鰭條胸鰭結構的驅動，并進行實驗測試了其運動性能。

4.2 俯仰與深度控制

上浮與下潛2種運動狀態是水下撲翼機器人完成深度控制的基礎。水下撲翼機器人機械機構設計的差異會導致其實現2種運動的方式不同[89]。例如，只擁有浮力系統的機器人可以在速度為零的情況下實現運動深度的改變，而只擁有重心調節機構的機器人則需要在機器人具備一定前游速度的基礎上，通過調節重心位置改變俯仰力矩，進而改變俯仰角，最后實現運動深度的調節。同時，擁有可上下偏轉的尾鰭的機器人也可以在具備一定的前游速度的基礎下通過調節尾鰭的偏置角度改變運動的深度[127]。當尾鰭向上偏置時，尾部受到的力會使得機器人產生抬頭力矩，機器人呈現上浮運動狀態，進而運動深度變小；當尾鰭向下偏置時，尾部受到的力會使得機器人產生低頭力矩，機器人呈現下潛運動狀態，進而運動深度變大。

由于尾鰭具有不占用額外的艙內空間、且結構設計相對簡單的優點，因此在進行水下撲翼機器人設計時，小尺寸樣機通常只包含尾鰭機構[127]，而大尺寸樣機通常同時包含重心調節機構與浮力系統[89]。

針對水下撲翼機器人深度控制，研究人員以盡量快速的按照平滑軌跡到達某一固定深度，并保持在這一深度游動為目標開展了相關研究。NIU等[127]通過調節尾鰭的偏轉角度，采用基于模糊邏輯的方法實現了機器人的深度控制，并通過實驗驗證了基于模糊邏輯的深度控制方法的有效性；WANG等[122]通過實驗研究了“RobCutt-I”的運動速度與波形傳動的運動學參數之間的關系，包括向前/向后游泳、潛水/上升和轉彎3個運動狀態，在此基礎上提出了將自抗擾控制（Active Disturbance Rejection Control，ADRC）與模糊策略相結合的混合控制，以實現深度和航向的閉環控制；德國EvoLogics GmbH公司與呂貝克應用科學大學[128]研制的Manta Ray AUV包括2個噴氣發動機、4個垂直推進器、2個機翼伺服系統、2個扭轉機翼伺服系統和1個尾部伺服系統，這種配置使得它具備動態深度控制能力，可以實現高精度的深度保持控制，同時具備迅速完成潛水或爬升動作的能力；CAO等[129]設計了一種仿牛鼻鲼機器人Robo-ray，通過2個尾鰭來實現該機器人的控制深度，基于CPG-模糊算法提出了開環速度控制、閉環深度控制和航向控制方法。閉環實驗結果表明，機器人的深度控制誤差小于6.1 cm，航向控制誤差小于6°；XIE等[86]考慮到未知的動力學和外部環境干擾，設計了一個基于CPG的經典高木–關野（Takagi- Sugeno，T-S）模糊神經網絡控制器用于仿蝠鲼機器人的航向和深度控制，并通過水池測試驗證了控制器的有效性，其深度跟蹤和航向跟蹤控制誤差分別為±6 cm和±6°；HE等[130]為了提高仿蝠鲼機器人的深度跟蹤能力，考慮仿蝠鲼機器人的縱向運動特性，設計了一個基于非對稱輸出S平面的深度控制器。最后，通過水池實驗驗證了仿蝠鲼機器人深度控制器的可行性和可靠性。實驗結果表明，深度控制誤差在±5 cm以內。

4.3 轉彎與航向控制

水下撲翼機器人的撲翼在撲動過程中的波動，可以簡單地分解為弦向的波動和展向的波動。水下撲翼機器人主要通過3種方式進行轉彎：兩側非對稱振幅方式和兩側鰭條間非對稱弦向相位差方式，以及非對稱振幅和非對稱相位差結合的方式[118，129]。

基于非對稱振幅的轉彎方式，一側撲翼的撲動振幅大于另一側，撲動振幅較大的一側產生更大的推進力，導致兩側撲翼的推進力不同，形成轉彎力矩[123]，從而使機器人轉向振幅小的或無拍動振幅的一側，實現航向的調整。基于非對稱振幅的轉彎模式具有較慢的轉彎角速度和較大的轉彎半徑，因此該方法適用于小范圍內的航向調整。

基于非對稱相位差的轉彎方式，撲翼的波動傳遞方向或快慢不同，因此兩側撲翼的推進力大小不同，形成一個大的轉彎力矩[123]。該轉彎方式主要用于快速響應時的機動轉向。因此，基于非對稱相位差的轉彎模式適用于轉彎角速度快、轉彎半徑小的大航向調整。

航向控制的主要任務是通過調節兩側胸鰭非對稱振幅及相位差，使機器人的實際航向趨近于期望航向。基于上述目標，WANG等[122，131]提出了一種ADRC與模糊控制策略相結合的混合控制方法來進行航向控制，該方法在實驗樣機RobCutt-I、RobCutt-II上進行了實驗，設定航向從70°調整到210°，穩定時間約為12 s，且超調量較小。針對單一依靠非對稱振幅及相位差進行航向調整存在的問題，HAO等[87]結合2種轉彎方式的特點，利用非對稱相位差快速調整航向，利用非對稱振幅精確調整航向，實現了閉環航向控制。通過航向干擾實驗，驗證了2種轉彎方式結合比單一方式更有效，并通過矩形軌跡游動實驗驗證了該機器人在2種轉彎方式結合下的機動性。此外，非對稱振幅可以提前改變預期的相位差，確保輸出的平穩過渡，實現快速準確的調整。針對上述航向控制方法精度不高的問題，XIE等[86]提出了一種將CPG和基于T-S模糊神經網絡（Neural Network，NN）的控制相結合的控制方案，該方法基于實驗數據構建航向數據集，并使用相應的數據集完成對所建立的T-S模糊神經網絡的訓練，提出了基于CPG網絡的航向控制器，其中參數由T-S神經網絡獲取，最后，實驗結果表明該仿蝠鲼機器人的航向控制誤差為±6°，航向控制精度有所提高，驗證了該控制器的有效性和魯棒性。HE等[130]以仿蝠鲼機器人在航向角變化較大的情況下實現良好的航向跟蹤效果為目標，結合模糊控制器和航向過渡目標值函數，基于S平面控制方法設計了仿蝠鲼機器人的航向控制器，最后，通過水池實驗驗證了蝠鲼機器人航向控制器的可行性和可靠性。實驗結果表明，航向控制誤差在±5°以內，與經典S面航向控制器相比，改進S面航向控制器的超調量較小，且航向切換后的誤差較小。

4.4 路徑點與路徑跟蹤

根據不同的控制目標，跟蹤問題可分為路徑點跟蹤和路徑跟蹤[132]。路徑點跟蹤的含義為機器人經過一系列給定的路徑點游動，路徑跟蹤的含義為機器人按照制定的最優幾何參考路徑游動[133-135]。

在運用路徑規劃算法規劃好一條從起點到目標點的最優路徑后，機器人從起點出發，按照某種控制規律進行運動，到達該最優路徑并實現對其的跟蹤。如何讓機器人跟蹤該最優路徑，是路徑跟蹤需解決的關鍵問題[136]。路徑跟蹤的實質是通過控制水下機器人的運動來減少機器人與參考軌跡之間的空間誤差。若考慮軌跡跟蹤，則需包含時間上的誤差。然而，水下撲翼機器人的模型不確定性和來自波浪和水流等環境的干擾在很大程度上影響著機器人的運動控制性能，進而影響跟蹤精度[137]。

針對上述路徑點跟蹤問題，BI等[138]提出了一種路徑點跟蹤控制系統，該系統包括2層：速度控制層和航向控制層。速度控制層基于實驗樣機與路徑點的距離調節機器人的最大撲動振幅，航向控制層采用模糊控制方法來獲得轉向運動的轉向因子。為了驗證控制系統的有效性，進行了路徑點跟蹤實驗，實驗結果表明，在任意設置路徑點或隨機給定路徑點的情況下，實驗樣機均能自主游動到達目標區域；WANG等[122]提出了基于有限狀態機（Finite State Machine，FSM）的視線（Line of Sight，LOS）制導系統的路徑點跟蹤方法，基于RobCutt-I實現了6個路徑點的跟蹤。

針對上述路徑跟蹤問題，WANG等[139]提出了一種用于三維點跟蹤的切換控制方法，并設計了一個模擬實際水下作業過程的實驗。實驗結果表明，RobCutt-II能夠跟隨參考路徑，且最大交叉軌跡誤差為0.1 m。隨后[140]，在該方法的基礎上進行改進，提出了一種將視覺系統與反步控制相結合的路徑跟蹤方法。仿真和實驗結果表明，RobCutt-II能夠在水下空間中自主地沿著直線和圓形路徑游動。此外，與傳統比例–積分–微分（Proportion-Integration-Differentiation，PID）方法相比，該方法減小了軌跡交叉誤差，軌跡跟蹤效果更加理想。同時，由于采用了航向補償，該方法具有較強的抗干擾能力。

4.5 避障與自主游動

水下撲翼機器人的高機動性使它們能夠在復雜和狹窄的環境中工作[141-142]。同時，自主工作的前提條件是機器人能夠自主檢測和避開障礙物。

目前，水下撲翼機器人大多采用紅外傳感器[141，143]、超聲波[144]、攝像頭[142]進行障礙物的檢測。ZHANG等[126]綜合昆蟲翅膀和魚鰭的優點開發了一款仿生機器魚，其頭部安裝了3個對前的紅外傳感器，包括上前、中前、下前3個方向，利用3個紅外傳感器的信息作為CPG網絡的反饋，機器人可以通過改變步態或動作來避開障礙物，實現自主游動。Festo公司仿生學團隊[144]設計Bionic Fin Wave的靈感來自于波浪狀鰭魚類的運動，該自主水下機器人能夠與外界進行無線通信，并將傳感器記錄的溫度和壓力值等數據傳輸到電腦上。此外，機器人前部還裝有壓力傳感器和超聲波傳感器以不斷地測量其與障礙物之間的距離，從而防止其與障礙物發生碰撞。XIE等[145]針對仿蝠鲼機器人自主游動的問題，在利用胸鰭相位差進行左右轉的基礎上引入飽和函數，使得機器人能夠根據障礙物的距離改變轉彎的速度。YANG等[146]針對已知結構化環境下的繞池壁自主游動問題，采用基于CPG、模糊控制與策略的控制方法，完成了仿蝠鲼機器人的水池繞壁自主游動。

4.6 基于相似度的運動參數優化

隨著水下撲翼機器人研究的深入，機器人在模仿真實生物時的重點由“形似”逐漸過渡到追求“神似”[147]。通過提高仿真度，可以顯著提升仿生機器人的穩定性、機動性和游動效率[84]。為了解決如何提高機器人運動姿態仿生相似度的問題，亟需建立基于仿生水下機器人的相似度評價體系，有效改善仿生機器人的運動特征和控制策略，進行機器人的運動相似度參數優化。

基于上述問題，MA等[148]通過特征點軌跡提取和動態時間歸整（DTW）算法建立了運動姿態的相似度評價規則。通過引入偏置方程和時間非對稱系數，建立了表征蝠鲼胸鰭運動時間和空間非對稱性的相位振蕩器模型，構造了基于相位振蕩器的CPG拓撲網絡。在此基礎上，建立了運動姿態相似度的適應函數，并提出了CPG網絡參數的遺傳粒子群優化算法，通過水池實驗驗證了基于相似度優化運動參數優化的控制的有效性。實驗結果表明，優化后的仿蝠鲼機器人前游運動姿態與蝠鲼的相似度提高到88.53%；隨后，該團隊研究了仿蝠鲼機器人胸鰭鰭條相位差變化的優化方法[149]，以輸出信號的平滑性和快速性為優化目標，采用非支配排序遺傳算法（NSAG-II）對CPG參數進行優化，得到最優參數組合。仿真和實驗結果驗證了優化后的CPG控制器輸出信號在相位切換過程中能夠平穩、快速地轉換。水下仿生撲翼機器人近年來發展情況如表1所示。

表1 水下仿生撲翼機器人近15年發展情況概述Table 1 Overview of the development of underwater bionic flapping wing robots in recent 15 years

綜上所述，基于CPG模型的方法被越來越多地使用到水下仿生撲翼機器人的胸鰭驅動上，該模型能夠在簡單的激勵輸入下模擬復雜的節律信號，具有很強的環境適應性，將傳感器信息耦合進CPG模型是水下仿生撲翼機器人撲翼驅動控制研究的新方向。在此基礎上，研究人員針對水下撲翼機器人的深度與航向控制問題，基于傳感器反饋采取合適的控制策略或無模型控制方法，通過改變水下撲翼機器人的俯仰與轉彎狀態實現深度與航向調節，從而實現深度與航向的控制。進一步地，水下撲翼機器人的路徑跟蹤與自主游動還需考慮機器人動力學模型的非線性與環境的不確定性，因此目前的研究成果多集中于單平面內的路徑跟蹤，而三維空間內的跟蹤問題仍處于初始階段。另一方面，仿生相似度評價方法的研究主要集中在仿生陸地生物和仿生機器人，對于運動機構具有明顯的主被動變形的水下撲翼機器人，完整的相似度評價體系還有待建立，且基于仿生相似度的運動姿態優化也存在較大的研究空間。未來，水下仿生撲翼機器人的多載荷應用、任務規劃與執行將是其成為海洋重要裝備的關鍵，其所涉及控制問題也值得研究人員去探索。

5 水下仿生撲翼機器人集群

與常規推進方式相比，魚類游動具有更高的效率、機動性、生物親和性和隱蔽性。近些年來，仿生集群逐漸成為水下機器人領域的一個研究熱點。

STEVENS等對蝠鲼種群進行了長達數十年的個體記錄與行為觀察，詳細闡明了蝠鲼個體與群體行為特征，根據蝠鲼的個體數量與運動類型，總結了蝠鲼個體與群體捕食策略，對于了解蝠鲼個體與群體行為特性提供了重要依據[151]。

GAO等和MA等采用數值模擬的方法研究了串聯、并排與垂直隊形下距離與攻角對蝠鲼個體與整體滑翔水動力性能的影響。從阻力性能方面，雙蝠鲼的串聯與并排隊形可以顯著降低整體阻力；垂直滑翔中，隨著攻角的變化，個體獲得阻力交替減小的效果。在升力性能方面，無論何種排列方式，滑翔時的整體升力與單體升力基本相同[152-153]。

國內外一些機構針對仿蝠鲼機器人的集群控制開展了相關研究。德國EvoLogics公司研發了BOSS-Manta Ray，搭載多型傳感器，技術成熟度較高。采用水聲通信方式，實現了3臺以上BOSS-Manta水下組網與集群，如圖9（a）所示，具備水文信息剖面測量、海底繪圖、協同監測和搜索等作業能力[154]。2021年，浙江大學設計了由介電彈性體和伺服電機混合動力驅動的軟體蝠鲼機器魚，并提出了一種基于全局視覺定位的機器人集群系統，實現了對自然界生物平行、圍捕和環繞3種典型的群集行為的模仿[105]。2022年，北京大學喻俊志團隊提出了一種基于視覺的仿蝠鲼機器人水下跟蹤方案，采用基于顏色的水下目標識別與定位方法，解決了機器人距離控制與方位控制耦合的問題，并通過水下實驗驗證了跟蹤方案的有效性和魯棒性[155]。2023年，西北工業大學將仿蝠鲼機器人的跟隨問題轉變為導引問題。基于魚群行為啟發，制定了基于跟隨區域劃分的群游跟隨導引策略，利用水下動作捕捉系統實現了仿蝠鲼機器人的跟隨游動控制[156]，如圖9（b）所示。

圖9 仿蝠鲼集群控制研究現狀Fig.9 Swarm control of manta ray-inspired vehicles

由于水下環境對感知和移動帶來了巨大挑戰，傳統的地面通信方法（如無線電）在水下表現不佳，而GPS等定位方法不可用。同時，水下移動面臨速度與加速限制等問題。目前，水下仿生撲翼機器人集群研究仍處于初始階段。

6 實驗研究

根據研究對象的不同可以將實驗研究分為生物游動實驗和仿生結構實驗。通過活體魚類尾跡流場實驗研究了解魚類游動特性，可為水下仿生結構設計奠定基礎；通過水下仿生結構實驗驗證結構性能，可為優化水下仿生結構提供參考。本節將對生物活體、仿生鰭結構以及仿生機器人的水動力與流場觀測實驗的研究進展進行回顧。

6.1 生物游動實驗

目前已有的生物游動實驗研究主要集中在利用粒子圖像測速（Particle Image Velocimetry，PIV）方法對BCF魚類的尾跡結構研究。PIV方法[157]通過高速相機捕捉待觀測區域示蹤粒子的速度場信息分析得出渦場結構。根據拍攝粒子運動的高速相機的數量，可將PIV實驗方法分為二維PIV實驗和三維PIV實驗。二維PIV實驗最少可通過一臺高速相機分析出待觀測流場切面中流體質點的兩個速度分量信息，稱為2D2C[158]方法。當有2臺及以上高速相機時，可以進行2D3C和3D3C[159]的PIV流場觀測實驗。2D3C方法的實驗待觀測區域仍為平面區域，但可分析出流體質點垂直于觀測面方向的法向速度分量。3D3C方法的實驗待觀測區域為具有一定厚度的三維空間，可分析出觀測區域內流體質點的3個速度分量。在重構三維流場的PIV實驗中，根據照射光的不同，又分為體光源照射實驗和激光斷層掃描實驗。前者通過捕獲區域內所有示蹤粒子的運動重構三維流場；后者通過測量若干不同切面的流動，利用插值算法重構三維流場。

1999年，DRUCKER等[160]在循環水槽的基礎上搭建了一個PIV觀測系統，用于研究翻車魚胸鰭尾跡的渦結構。為保證觀測過程中魚體與觀測區域相對靜止，將水槽中的流速設定為翻車魚的游速。通過對翻車魚俯視面、縱平面、橫截面的流場進行觀測，得到了對應的速度場信息。根據DICKINSON等[161]得到的尾跡動力學公式，得出了翻車魚胸鰭尾跡中渦環的動量角、射流角、渦環直徑、渦環面積、平均渦環環量以及渦環動量的大小。2000年，DRUCKER等[162]通過PIV實驗研究了沖浪鱸魚和翻車魚的游動尾跡渦結構，以揭示導致魚類游動速度不同的機理。實驗結果顯示，2種魚類在不同的游動速度下尾流中的射流角和動量角存在較大差異。2001年，DRUCKER等[163-164]研究了翻車魚不同鰭尾流的渦場結構。翻車魚的胸鰭、尾鰭和背鰭對于恒定直游時推力的貢獻分別為50.0%、37.9%和12.1%。對于轉彎時的側向力，三者的貢獻分別是65.1%、34.9%和0，研究結果說明翻車魚可以利用背鰭處的渦流來增強推力。DRUCKER等[165-168]針對魚類游動的PIV實驗證明了利用PIV實驗方法重構魚類尾跡流場的可行性，通過分析不同尾渦結構的差異，可以揭示魚類推進的水動力規律。

2004年，TYTELL等[28，169]利用PIV方法研究了鰻魚的尾跡結構，并驗證了鰻魚游動尾跡中渦環不連續的猜想。實驗結果表明，鰻魚的尾跡渦結構中，側向的射流在流場中獨立存在，尾部區域具有渦量較大的脈沖射流。

6.2 仿生結構實驗

水下仿生結構的實驗可以分為力學實驗和流場觀測實驗。胸鰭結構的推力和效率是學者們主要關注的力學性能。根據二維不可壓縮流體的無量綱的N-S方程，可以推導得到斯特勞哈爾數（Strouhal Number，St）St=l/τv，此無量綱數反映了結構的特征長度、周期運動頻率以及與流體環境的相對速度。因此，在研究仿生胸鰭結構周期性往復拍動的運動場景時，St是主要考慮的無量綱數。

1993年，TRIANTAFYLLOU等[170-171]在循環水槽中搭建了測量振動翼水動力的實驗平臺，并測得推力系數和效率關于St的變化曲線。實驗結果表明，當St處于0.2～0.35時，振動翼的效率達到峰值，這與大多數生物游動時的St范圍一致。此外，他們還通過染色法展示了翼板后方反卡門渦街演化的過程。1998年，ANDERSON等[172-174]在Triantafyllou水動力實驗的基礎上，使用PIV設備進行了振動翼尾跡的渦場結構分析實驗。通過對振動翼進行變翼型弦厚比、攻角和振蕩角的水動力實驗，發現推力系數與St之間存在顯著的正相關關系，效率呈現出先增后減的趨勢。不同工況的實驗中峰值效率對應的St存在差異。PIV的實驗結果表明當振蕩幅度較小、St處于中低水平時，在半個周期內（上沖程或下沖程），振動翼將脫落出一個單渦（2S）；當震動幅度較大或St處于較高水平時，半周期內振動翼將脫落出一個對渦（2P）。

1998年，KATO[175]根據鱸魚的外形設計了一個胸鰭撲動仿生樣機，胸鰭根部由2個旋轉軸垂直的電機連接并驅動。實驗結果表明，當2個電機的輸出相位差為90°時，胸鰭的推力效率最高。

2003年，READ等[176-178]在可調攻角的翼型水動力實驗平臺上，進行了翼型關于最大攻角、St和振蕩角的水動力實驗，并繪制了關于翼板攻角和St的推力系數、效率的云圖。推力系數的云圖表明，當St和攻角同時增大時，推力系數隨之增大并逐漸收斂。效率的云圖表明，在低St（St=0.1）下，翼板攻角的可調節范圍相對較大；隨著St增大至0.2以上時，為保證效率不變，翼板的攻角須急速地下降，在St在0.2～0.6范圍內，效率最高可以達到0.6。這一攻角急速下降的現象與飛機機翼的失速效應類似。

2005年，BUCHHOLZ等[179]利用染色法對NACA翼型振蕩翼板的尾跡結構進行了研究。染色法的原理是在被測結構物前緣左右兩側及上下兩面，分別設計可與外界染色物質相連的小孔，由小孔不斷輸送染色物質到流場中，染色物質可以顯示被測結構物周圍的流場變化情況。BUCHHOLZ的實驗較為完整地展示了不同觀測面下，從翼板脫落的馬蹄渦的演化過程，以及渦街在不同截面處的結構。

2008年，GREEN等[180]在Smits振蕩翼尾跡結構研究的基礎上，通過在翼板的特征點處安裝多個壓力傳感器，捕捉翼板振蕩時表面壓力的變化。實驗結果表明，某一點處壓力的變化隨著翼板正弦形式的振動呈現出非對稱的周期性變化。尾跡渦結構的實驗結果表明，當振動幅度增大，或者St增加時，尾渦結構會由2S結構逐漸變化為更為復雜的2P結構，這一結果與ANDERSON的實驗結果類似。

2008年，HEATHCOTE等[181]采用斷層式PIV方法，進行了不同厚度下NACA翼型振動翼的水動力及尾跡渦結構觀測實驗。實驗結果顯示，在不同的St下，隨著振動翼厚度的逐漸增加，推力系數與推進效率先增大后減小，推進效率最大值為0.27。PIV實驗結果表明，靠近翼根處的截面渦結構與靠近翼梢處的截面渦結構具有較大差異。

2010年，RIGGS等[182]對比了2種不同剛度的硬質NACA翼板和柔性仿太陽魚鰭板的推進特性。實驗結果表明，在不同的振幅和頻率下，無論是硬質翼板還是柔性鰭板，仿生鰭板的推力顯著高于NACA翼板的推力。在側向力與推力組成的圖中，由于一個拍動周期內力學特性呈現出周期性變化，因此側向力與推力組成一個封閉曲線。在側向力相同的情況下，仿生鰭板的推力整體在NACA0012翼板之上。

以上是眾多學者對于BCF魚類和NACA翼型鰭板進行的水動力及流場實驗研究，對于MPF推進方式的仿生結構的實驗研究出現較晚。

2006年，CLARK[183-184]在上述染色法實驗的基礎上做了進一步的研究。他們采用具有柔性的PVC材料，參照蝠鲼的外形將翼板的形狀調整為類橢圓形。通過多個電機軸并聯的方式，在翼面上制造行波。翼的上表面連接紅色染色物質，下表面連接綠色染色物質，以此來區分翼在運動過程中上下沖程不同的渦結構演化。尾跡結構分析結果表明，在振動翼板的后方演化出兩條上下渦旋方向相反的射流。2009年，CAI等[72，74，125，185]以蝠鲼為仿生原型設計了仿蝠鲼機器人。其內部嵌入了氣動結構，由外部氣源驅動，游動速度較慢。通過水動力實驗，測得該仿生結構的力–St曲線與效率–St曲線。實驗結果表明，這些曲線的趨勢與之前提到的翼板對應數據的趨勢相似。同年，MOORED等[186]以牛鼻鲼為仿生原型設計制作了撲翼機構，為實現波動傳遞將撲翼沿展向切分為多個相連部分。利用染色法對前后緣脫落的尾渦結構進行分析后，觀測到了Clark染色法實驗未曾觀測到的撲翼前緣脫落渦。

2011年，DEWEY等[187]在Smits染色法測尾跡渦結構的實驗基礎上，將觀測手段改為PIV方法，并將振蕩翼板的結構改為具有波動傳遞的仿蝠鲼胸鰭結構。實驗結果表明，St和胸鰭上行波的波長是影響胸鰭后緣渦脫落分裂的主要因素。行波波長減小將促使單個振動周期內脫落的渦旋由單個變為一對，St增加將使得沿出射角脫落的相鄰分離渦的距離減小。相比之下，2009年，SCHNIPPER等[188]通過改變振動翼的頻率和幅度，捕捉到了尾跡渦旋由2S變為2P、2P-2S、4P、8P的結構演化特性，對應的單個周期內的渦旋數分別為2、4、6、8、16。尾跡渦旋的演化過程為，起始渦在翼型前緣和后緣分別脫落后，不斷夾帶流體質點使得渦核逐漸增大，在達到形成數之后不再繼續增加渦量。

上面提到的“形成數”是渦旋由起始到演化再到渦量不再增加的無量綱時間，由GHARIB等[189]于1998年提出，并由DABIRI等[190]持續發展。考慮振動翼和仿生翼尾跡的渦旋演化場景，影響其尾渦結構演化的關鍵因素為流場速度和結構物的特征長度。

2014年，牛傳猛等[45，191-193]基于牛鼻鲼的外形以及運動規律設計了仿生魚，并搭建水動力實驗平臺進行了推力和升力關于振動幅度、頻率以及舵機輸出角度相位差的實驗。實驗結果表明，振動幅度與推力和升力之間呈正相關關系，而頻率在小于0.8 Hz時與推力之間呈正相關關系，大于0.8 Hz時呈負相關關系，推力效率在St為0.4時達到峰值。2017年，CHEW等[194-196]基于蝠鲼生物外形設計制作了仿生魚實驗平臺，胸鰭結構采用單鰭條覆以二維PVC薄膜的形式。在不同胸鰭根弦比、后掠角、鰭條剛度等胸鰭結構參數下進行水動力實驗。實驗結果表明，根弦比代表的弦向柔性增大時，推力系數變化不大，而效率持續降低；展向鰭條厚度即展向柔性增大時，推力系數在呈現一定增長趨勢后迅速衰減；后掠角對于仿生胸鰭的推力系數影響不顯著。2021年，XING等[88]以蝠鲼為仿生原型設計了可展弦向波動傳遞的仿生水動力實驗平臺，針對仿生胸鰭的2自由度運動，研究了胸鰭振動的幅度、頻率、俯仰角度以及初始偏置對于其水動力性能的影響。實驗結果表明，在普遍的工況設置下，推力在周期內都呈現出高低雙峰，平均推升力在不同的頻率設置下與振動幅度呈顯著的正相關關系。

針對魚類和水下仿生結構的實驗研究主要分為水動力實驗和流場觀測實驗兩類。學者們針對魚類和仿生結構進行了系列化的實驗研究，得到結構特性和運動參數對水動力特性影響的規律。但已有的實驗研究主要關注魚類/仿生結構尾流渦場結構的演化，以及全約束模型的水動力特性和流場特性。仿生結構表面處的流場演化、無運動約束的仿生鰭結構實驗研究方面還處于初始階段。

7 結束語

目前的水下仿生撲翼機器人研究雖然已在各方面取得了長足的進步和發展，但仍存在諸多不足，面臨巨大挑戰。例如：伴隨結構非線性變形的流固耦合問題，仿生驅動結構方面存在的變剛度調節與柔性分布調節問題，水下仿生集群方面存在的自我感知與相互感知等問題，這些都限制了水下仿生撲翼機器人的進一步發展。

隨著相關仿真計算方法、實驗測試方法等的進步，研究者們對相應推進機理的認識將會進一步完善，仿生樣機的各方面性能也將會得到進一步提升、逐漸縮小與真實生物的差距。水下仿生撲翼機器人也將會在水下信息采集、海洋牧場養殖、廣域海洋監測等領域得到更多的發展和應用。