基于線控轉向的差動轉向控制策略研究

王家鑰, 常九健

(1.合肥工業大學 汽車與交通工程學院,安徽 合肥 230009; 2.合肥工業大學 汽車工程技術研究院,安徽 合肥 230009)

近年來,在節能減排上有著重要優勢的新能源汽車取得巨大發展,汽車工業已將新能源汽車列為研究重點之一。分布式電驅動汽車因其具有體積小、質量輕、效率高、控制性能良好以及能將電動車輛的機械部分大大簡化的優勢和特點,得到了學術界和工業界的高度關注。

傳統履帶車的滑動轉向給出了差動轉向設計思路,研究者于1999年提出了通過改變差動力矩轉向方式的概念,經過多年發展形成了差動轉向技術。文獻[1]采用了基于線控轉向的差動轉向控制策略,設計當線控轉向系統故障時的差動轉向輔助控制,考慮線控轉向系統和懸架對差動轉向的影響,基于輸出反饋理論主要研究車輛差動轉向的防側翻控制,提高了汽車在垂直方向上的穩定性;文獻[2]在路徑跟蹤問題的基礎上重新定義橫擺角速度期望值,實現對期望橫擺角速度和側向速度的跟蹤,采用線性時變模型來預測未來某一時間段的系統響應,采用動態規化算法對橫擺角速度實現閉環控制,將路徑跟蹤問題轉化為無人駕駛車輛行駛穩定性問題;文獻[3]通過BP神經網絡訓練各工況理想阿克曼轉向關系下的各車輪輪速和驅動力矩來直接實現差動轉向,但對汽車滑移率的控制效果較差;文獻[4]設計了變結構滑模控制器,通過DYC&AFS的協同控制使汽車橫擺角速度和質心側偏角趨于理想值,但在質心側偏角過大時,車輛無法再按期望路徑行駛,喪失穩定性。

上述文獻多以橫擺角速度和質心側偏角[5]作為穩定性控制指標,但汽車線性二自由度車輛模型對質心側偏角計算不精確,容易造成以差動轉向汽車作為轉向策略的整車因側傾而喪失穩定性。本文基于線控轉向執行機構,以橫擺角速度和期望路徑為穩定性控制指標,研究一種協同控制策略,其中包括差動轉向控制策略和路徑跟蹤控制策略。

通過輪轂電機驅動汽車的各車輪獨立可控制的優勢,對電動汽車各輪轉矩和轉速進行直接控制。因此本文以此設計控制器控制左右車輪的驅動力矩差,產生額外的橫擺力矩[6],一方面可以直接作用于轉向系統使車輪向驅動力矩小的一側轉動,另一方面可改善車輛的穩定性。差動力矩不可直接應用到各車輪,本文建立下層控制器將上層控制器得到的差動力矩分配[7]到各驅動車輪,以驅動車輪轉向。同時,本文提出以期望橫擺角速度和期望路徑作為穩定性判斷指標,研究一種基于路徑跟蹤的控制策略,修正電動汽車前輪轉角[8]來減小與期望路徑的誤差,提升汽車的橫向穩定性。

1 協同控制策略原理

本文以線控轉向機構為轉向執行機構,在本文設計的差動轉向算法下實現駕駛員的目標轉向,同時以車輛橫擺角速度和期望路徑為標準實現車輛穩定性控制,提升差動轉向的可行性。本文所設計的協同控制策略流程如圖1所示。

圖1 協同控制策略流程

協同控制策略實現過程如下:

1) CarSim輸出車輛縱向車速vx和實時方向盤轉角δ到二自由度車輛模型,得到理想橫擺角速度ωd。

2) 滑模控制器得到實際橫擺角速度ωr、實際質心側偏角β和理想橫擺角速度ωd,計算得到差動轉向所需橫擺力矩。

3) 下層轉矩分配器計算得到各輪的轉矩T。

4) CarSim將車輛橫向車速vy、橫擺角φ、車輛實際路徑輸入線性二次型調節器(linear quadratic regulator,LQR),同時將車輛期望路徑輸入LQR控制器,得到前輪附加轉角δfex。

5) 車輛經下層轉矩分配器重新分配各輪轉矩T,輸入CarSim車輛模型,實現差動轉向;同時,LQR控制器得到前輪額外轉角δfex,輸入CarSim(由線控轉向機構作為執行機構),實現對期望路徑的跟蹤。

2 差動轉向控制策略設計

2.1 整車動力學建模

本文選用線性二自由度車輛模型[8]作為參考模型來獲取操縱穩定性控制所需的橫擺角速度,參考模型如圖2所示,整車模型主要參數見表1所列。

表1 整車模型主要參數

圖2 二自由度汽車模型

車輛二自由度狀態方程如下:

(1)

其中

其中:k1為前輪側偏剛度;k2為后輪側偏剛度;m為質量;a為質心到前軸的距離;b為質心到后軸的距離;vx為車速;β為質心側偏角;δ為前輪轉角;Iz為車輛縱向轉動慣量。由此可得線性二自由度車輛模型動態變化的理想橫擺角速度ωr。

理想橫擺角速度受輪胎側向力極限和路面附著系數的制約,因此考慮滿足不同路面附著系數的理想橫擺角速度為:

(2)

其中:K為穩定性因素;μ為路面附著系數;g為重力加速度。

2.2 滑模控制器設計

本文采用滑模變結構控制器[9],其具有快速響應、設計簡單的特點,對外界干擾有較強的魯棒性,能夠克服系統的不確定性。

考慮差動力矩,得到基于車輛二自由度狀態方程的差動轉向的狀態空間方程,即

(3)

滑模控制器設計選擇對理想橫擺角速度和實際橫擺角速度的差值e進行控制。

選擇切換面函數為:

(4)

對切換函數求導可得:

(5)

選擇為了使系統能夠快速收斂到滑模面,減小抖振,采用冪次趨近率,即

(6)

其中:ε為系統趨向于滑模面的速度,ε越大速度越快,但引起的抖動也越大;α控制系統在遠離滑模面時快速趨于滑模控制面,在趨于滑模面時控制系統抖振動。為消除由冪次趨近率帶來的滑模抖振,采用飽和函數sat代替符號函數sgn,即

(7)

聯立式(4)～式(8)可得所需理想差動力矩為:

(8)

2.3 下層控制器設計

上層控制器得到的差動力矩無法直接應用到輪轂電機驅動汽車上,需要設計下層力矩分配器來分配各車輪所需驅動力[10]。

將總驅動轉矩Tq進行載荷轉移動態分配[11],考慮縱向加速度ax的影響,前、后軸的載荷可表示為:

(9)

其中:Fzf、Fzr分別為前軸和后軸的垂直載荷;hg為質心高度。根據前、后軸的動態載荷比分配前、后軸驅動力矩為:

(10)

其中:Tf、Tr分別為前軸和后軸的驅動力矩。

車輛轉向時存在的側向加速度ay會導致左右車輪之間的載荷轉移,差動轉向同樣要考慮左右車輪的垂直載荷來分配各輪驅動力矩,各車輪的垂直載荷為:

(11)

其中:Fzfl、Fzfr、Fzrl、Fzrr分別為左前輪、右前輪、左后輪、右后輪的垂直載荷;d為輪距。

經動態分配后的各輪驅動力矩為:

(12)

其中:Tfl、Tfr、Trl、Trr分別為左前輪、右前輪、左后輪、右后輪的驅動力矩;Reff為輪胎有效轉動半徑;lc為輪距的1/2。

3 路徑跟蹤控制策略設計

3.1 路徑跟蹤模型

路徑跟蹤的目標[12-13]為減小車輛與期望路徑的橫向誤差和航向誤差,原理圖如圖3所示,圖3采用自然坐標系。

圖3 路徑跟蹤模型

圖3中:點T為車輛真實位置在期望路徑上的投影點;d為本文定義的橫向誤差;ψ為航向誤差,ψ=θ-θd;點C為車輛質心;X為車輛真實位矢;Xr為車輛目標位矢。路徑跟蹤通過對前輪轉角的修正來減少橫向誤差和航向誤差。

3.2 建立控制目標狀態空間方程

車輛二自由度動力學方程為:

(13)

其中

定義真實位矢X與目標位矢Xr的矢量差為誤差er,u為前輪轉角,可得關于誤差er的方程為:

(14)

(15)

其中:v為車輛質心的速度矢量;k為T點處的曲率。

橫向誤差的導數為:

(16)

令ed=d,eφ=φ-θd,其中,φ=θ-β,β為質心側偏角。

(17)

整理得狀態方程:

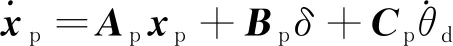
(18)

其中

3.3 設計路徑跟蹤控制器

3.3.1LQR反饋控制器設計

LQR通過權矩陣Q和R確定二次型目標函數J的最小值,可得最優的狀態線性反饋控制規律,易于構成閉環最優控制,并可兼顧多項性能指標。

本文設計的LQR控制器需將狀態方程(18)離散化為:

(19)

由Riccati方程求解P,即

迭代得:

(20)

3.3.2 前饋控制器設計

(21)

記

(22)

為消除穩態誤差err,引入前饋控制δfex,即

err=

求得ed=0時的前輪附加轉角,即

(23)

引入前饋控制后,有

u=-Ker+δfex

(24)

其中,u為式(19)的控制量,通過前輪附加轉角對前輪轉角的修正,可減小真實位矢X與目標位矢Xr間的誤差er[14]。

4 仿真分析

為驗證算法的有效性,本文以國標GB/T 12549—2013中的移線試驗(lane change test)和蛇形試驗(pylon course slalom test)來驗證汽車的機動性、響應性和穩定性,以此來評價算法的有效性。

移線試驗道路標準為:以(80±3) km/h的速度行駛通過,試驗車道如圖4所示。

圖4 移線試驗車道

圖4中:第1段長70 m;第2段長20 m;第3段長30 m;第4段長20 m;第5段長10 m;6為車道偏移,為3.5 m。蛇形試驗標準為:以(60±3) km/h的車速,繞間距18 m的標樁行駛。

本文選取以上2種工況,比較輪轂電機驅動汽車在無控制、滑模控制、滑模控制與路徑跟蹤控制綜合的控制器(下文稱綜合控制)下的控制效果。

4.1 移線試驗

在80 km/h時速移線試驗中,橫擺角速度變化如圖5所示。

圖5 移線試驗橫擺角速度變化

在80 km/h時速移線試驗中,無控制時的滑移率變化如圖6所示,經綜合控制的滑移率變化如圖7所示。

圖6 移線試驗無控制時滑移率變化

圖7 移線試驗綜合控制下滑移率變化

在80 km/h時速移線試驗中,各控制策略下路徑如圖8所示。

圖8 移線試驗各控制策略路徑

4.2 蛇形試驗

在60 km/h時速蛇形試驗中,橫擺角速度變化如圖9所示。

圖9 蛇形試驗橫擺角速度變化

在60 km/h時速蛇形試驗中,無控制時的滑移率變化如圖10、圖11所示,其中圖11是圖10的部分放大;經綜合控制的滑移率變化如圖12所示。

圖10 蛇形試驗無控制時滑移率變化

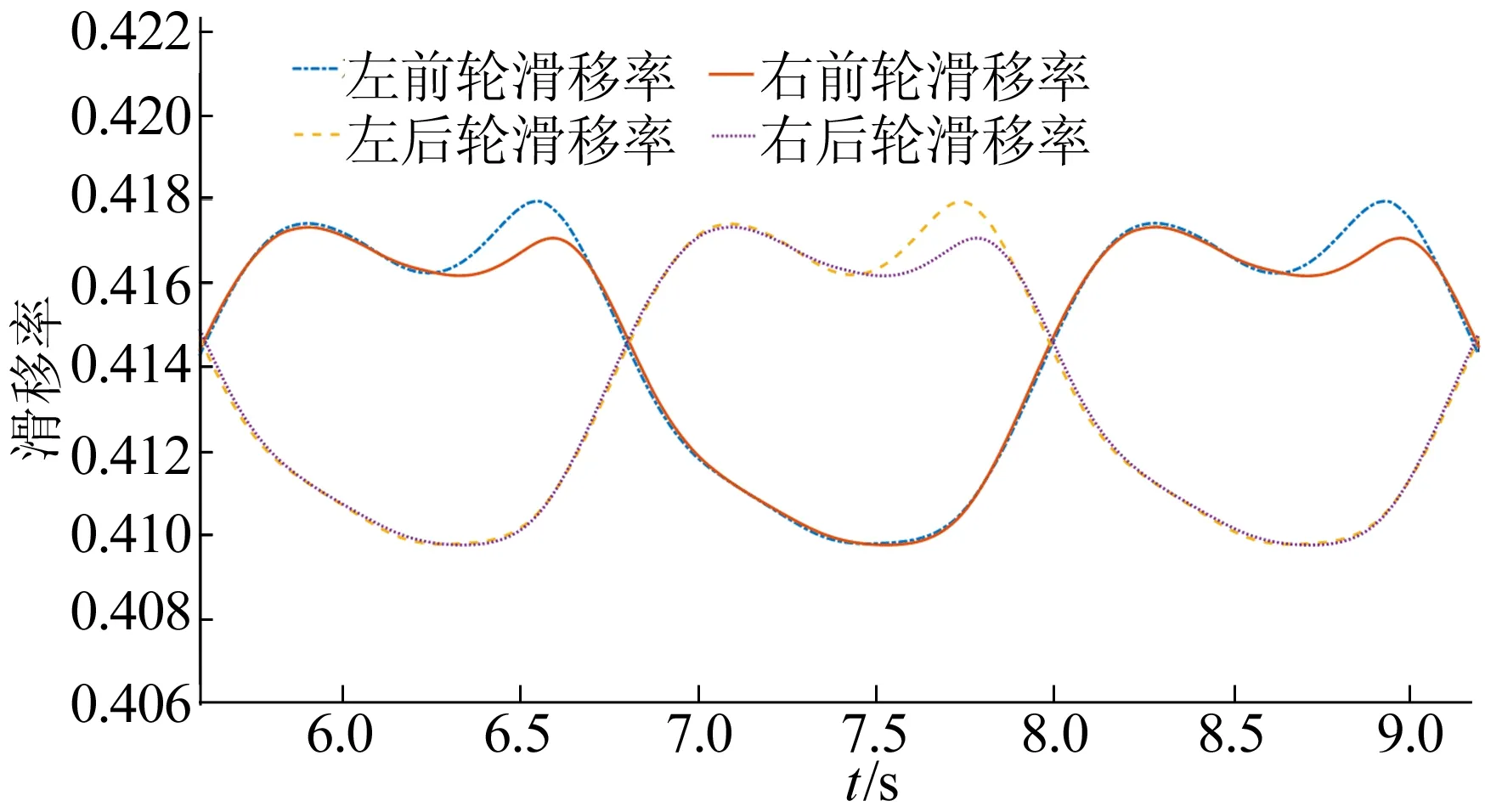
圖11 蛇形試驗無控制時滑移率變化部分放大

圖12 蛇形試驗綜合控制下滑移率變化

在60 km/h時速蛇形試驗中,各控制策略下路徑如圖13所示。

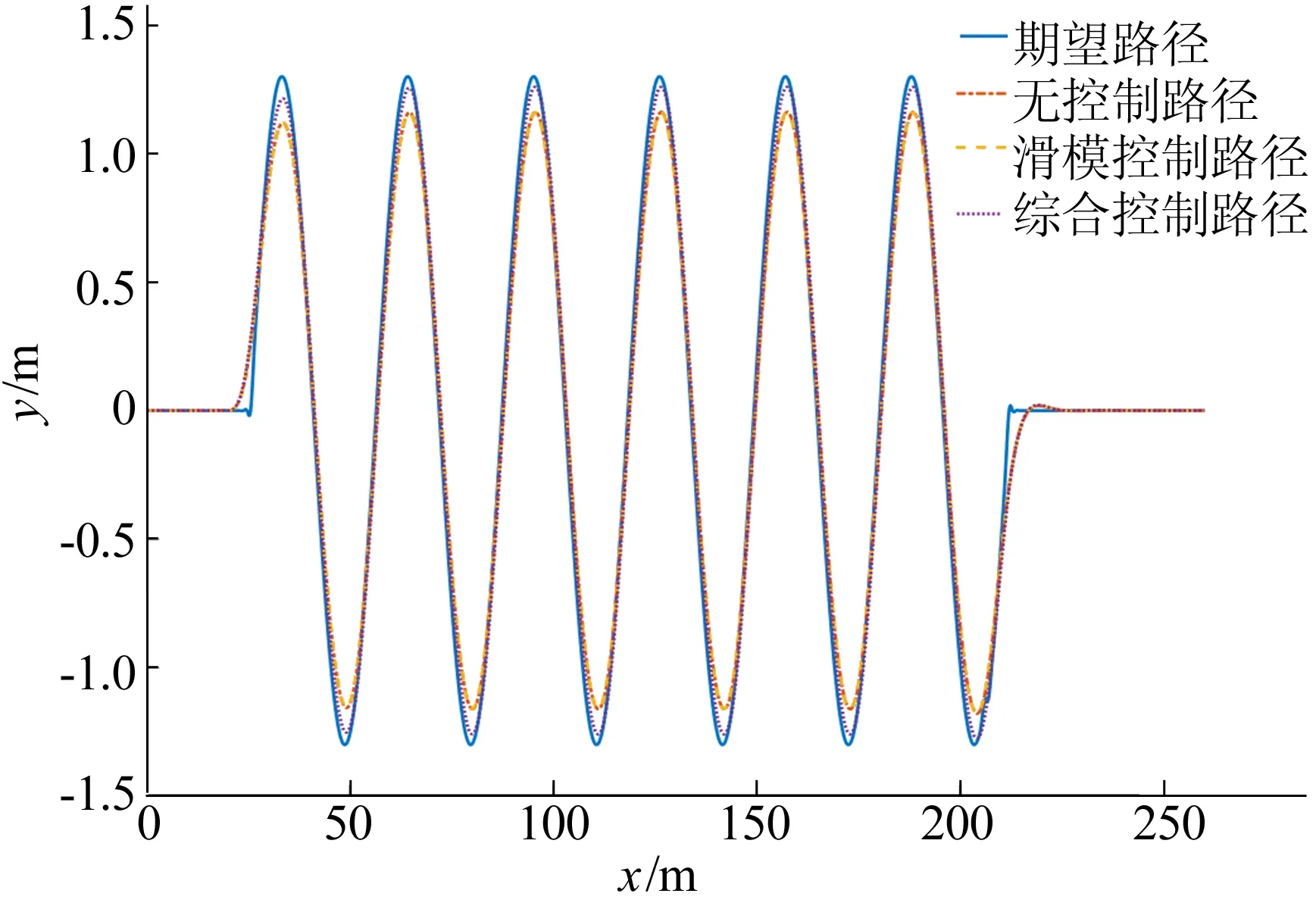
圖13 蛇形試驗各控制策略路徑

由圖5、圖9可知,在移線試驗和蛇形試驗中,車輛理想橫擺角速度由汽車線性二自由度狀態方程計算得出,采用滑模控制器單獨實現差動轉向時,車輛橫擺角速度較無控制組有大幅下降,趨于理想值;采用綜合控制時,車輛橫擺角速度進一步貼近理想值,在移線試驗中,車輛實際橫擺角速度曲線幾乎與理想橫擺角速度曲線重合。試驗證明,本文設計的控制策略對車輛響應性、穩定性有較好提升。

由圖6、圖7、圖10～圖12可知,在移線試驗和蛇形試驗中,無控制時分布式電驅動整車滑移率較高,而在本文設計控制策略下,車輛滑移率得到了有效控制,車輛操縱穩定性得到了有效保證。

由圖8、圖13可知,在移線試驗和蛇形試驗中,在本文設計控制策略下,車輛路徑與期望路徑誤差較無控制時大幅下降。其中,蛇形試驗路徑變化更加明顯,本文設計期望路徑縱向偏移為1.3 m,在無控制下的車輛路徑與期望路徑最大縱向誤差為17 cm,綜合控制下的車輛路徑與期望路徑最大縱向誤差為8 cm,證明本文設計路徑跟蹤控制器有效。

5 結 論

本文首先確定了分布式電驅動整車差動轉向所需差動力矩的狀態空間方程,然后設計了差動轉向控制器和路徑跟蹤控制器,確定了基于橫擺角速度和期望路徑的綜合控制策略,并基于計算得到的差動力矩對各車輪驅動力矩進行動態分配。最后在移線試驗和蛇形試驗下進行了仿真試驗,驗證了本文提出的差動轉向的有效性。

試驗對比發現,經滑模控制器實現的差動轉向控制策略,可通過差動力矩的計算和分配,車輛穩定性和響應性較傳統線控汽車有大幅提升;而通過路徑跟蹤控制器補償的前輪額外轉角,使得汽車在綜合控制下進一步提升了車輛的響應性和穩定性。在2個典型工況中,綜合控制策略下的車輛實際橫擺角速度和理想橫擺角速度的誤差大幅下降;綜合控制策略下的車輛實際路徑和期望路徑誤差亦得到有效控制。證明本文設計的控制策略有效提升了分布式電驅動整車在行駛時的穩定性和路徑跟蹤的精度。