一種采用平行接近策略的三維制導律

王亞鋒，喻夏瓊，范開國，徐東洋

（32021部隊，北京 100094）

0 引言

導彈制導律設計一般采用兩種思路：一是通過小量假設解耦俯仰、航向和滾轉三通道，分別設計制導律；二是三通道整體設計。現有制導律設計方法主要包括兩類：一是追蹤法[1]、平行接近法、三點法[2]和比例導引法[3-8]等經典方法；二是應用最優理論[9]、變結構理論[10]、模糊理論[11]、自適應理論[12]等現代方法。有些現代方法由于充分考慮了自動駕駛儀特性[13-14]和末端約束（時間、角度、速度等）[15-16]，引起了大量學者的關注。從理論上講，平行接近法是最優接近策略，但受限于硬件條件，實現難度很大。工程上，主要采取比例導引法，導彈法向、側向加速度指令分別成比例于視線仰角速率和視線偏轉角速率。但是，傳統比例導引法所生成的彈道角并不是最優的，因為平行接近策略下，最優彈道角是由導彈和目標的相對位置關系和運動狀態唯一確定的。

本文提供了1種采用平行接近策略的導彈三維制導律設計方法。該方法基于導彈和目標的相對位置關系和運動狀態，計算得到最優彈道角。運用反饋線性化方法，設計期望彈道偏角速率和期望彈道傾角速率，轉換得到最終的三維制導指令。通過對最優彈道角的逼近，控制導彈與目標平行接近，實現導彈對目標的打擊。

1 導彈的動力學方程

彈道坐標系下，導彈的動力學方程為：

式（1）中：m為導彈質量；v為導彈速度；P為導彈發動機推力；G為導彈所受的重力；X為導彈所受的阻力；Y為導彈所受的升力；Z為導彈所受的側向力；α為攻角；β為側滑角；γv為速度傾斜角；ψv為彈道偏角；θ為彈道傾角。

2 相對運動模型

導彈運動學方程為：

彈目相對運動方程為：

3 平行接近策略的實現思路

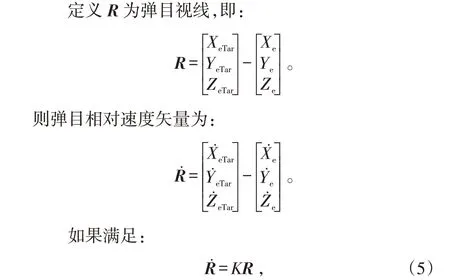
則導彈最終將與目標遭遇，即R→0。

式（5）中，

為比例系數，滿足k1<0,k2<0,k3<0。

不難看出，當k1=k2=k3=k時，導彈對目標的追蹤策略就是平行接近法，k即待求的平行接近速率。顯然，采用平行接近法時，導彈速度矢量須滿足：

式（7）中，目標速度矢量vTar和彈目視線R由導彈導引頭或我方其他平臺的觀測數據通過濾波算法得到。理想情況下，若導彈速度矢量v的兩方面都是可控的，即速度大小（由v表征）和速度方向（由ψv、θ表征）可控，則可實現：t→+∞時，R→0。

但是，導彈速度v通過改變發動機推力P的大小實現，彈道偏角ψv和彈道傾角θ通過操縱導彈的舵偏實現。通常情況下，因硬件條件所限，發動機推力大小是個分段常值，開機為額定推力值，關機為0。有些導彈會在突防階段加力，但也只能階躍式加力，無法實現連續性大小調節。所以，在制導律設計中，可認為導彈速度是不可控的，導彈對目標的追蹤只通過操縱舵偏實現。

v=vTar-kR的成立包含兩個方面：大小一致和方向一致。從大小一致方面講，由于導彈速度和目標速度不可控，只能通過平行接近速率k的設計滿足；從方向一致方面講，在設計好k以后，通過控制導彈的速度方向（彈道偏角ψv和彈道傾角θ）實現。

平行接近策略分4步實現：第1步，計算平行接近速率k，以滿足大小一致；第2步，計算彈道偏角ψv和彈道傾角θ的期望值，以滿足方向一致；第3 步，設計彈道偏角速率和彈道傾角速率的期望值；第4步，轉換得到過載指令。

4 平行接近速率的求取

平行接近速率k通過滿足大小一致條件求取：

a存在2個實數解：

k的實部為負，導彈可以擊中目標；當vTar≥v、vTar?R≥0 時，k不存在實部為負的根，導彈無法擊中目標。

5 期望彈道偏角和彈道傾角的求取

6 過載指令的設計

得到彈道偏角和彈道傾角的期望值后，對比當前實際彈道偏角和彈道傾角，通過反饋線性化方法求取得到彈道偏角速率和彈道傾角速率的期望值C(θ? )、C(ψ?v)：

式（16）中，nψv,max為側向過載限幅。

7 仿真算例

以某型空空導彈為例，參數設置如下。

初始位置：

圖1 彈道角度變化曲線（情況1）Fig.1 Change curve of trajectory angle in case 1

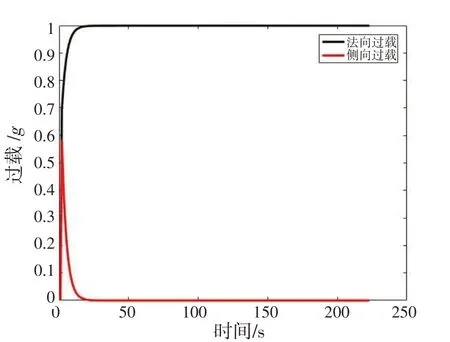
圖2 過載指令（情況1）Fig.2 Overload command in case 1

圖3 彈目相對運動示意圖（情況1）Fig.3 Relative motion of missile and target in case 1

這種情況表示目標作勻速直線運動，速度大于導彈速度，彈道角設置為與導彈作相向運動。圖4～6 顯示了這種情況下，導彈依然能夠按照平行接近策略擊中目標，原因是導彈與目標的相向運動，使得平行接近速率k仍然存在負實數解。但是，與情況1相比，導彈在調整彈道角時需要的過載更大一些。

圖4 彈道角度變化曲線（情況2）Fig.4 Change curve of trajectory angle in case 2

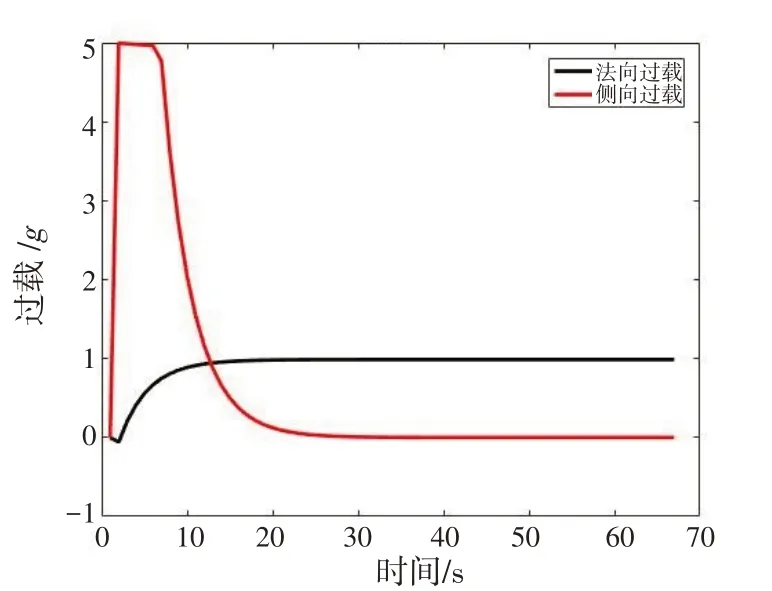
圖5 導彈過載指令（情況2）Fig.5 Overload command in case 2

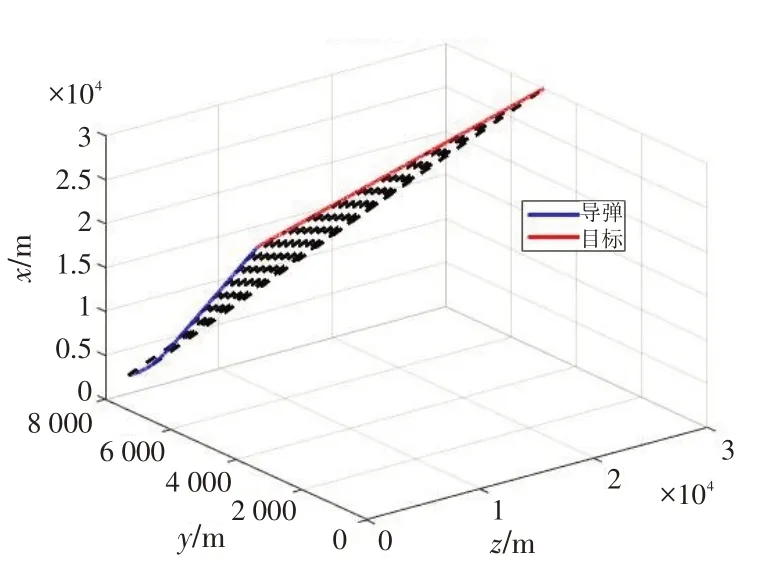
圖6 彈目相對運動示意圖（情況2）Fig.6 Relative motion of missile and target in case 2

這種情況表示目標中途發現導彈后，機動調整方向，加速逃離。從圖7 可以看出，除了初始時刻以外，導彈在t=50 s 時刻也在調整彈道角，原因是此時目標在作機動逃離。圖8顯示了與其對應的過載指令。整個過程中，由于目標速度一直小于導彈速度，平行接近速率k的負實數解始終存在，所以導彈仍然能夠按照平行接近策略擊中目標，如圖9所示。

圖7 彈道角度變化曲線（情況3）Fig.7 Change curve of trajectory angle in case 3

圖8 導彈過載指令（情況3）Fig.8 Overload command in case 3

圖9 彈目相對運動示意圖（情況3）Fig.9 Relative motion of missile and target in case 3

情況4與情況2的相同之處在于目標都是作勻速直線運動且速度大于導彈速度。不同之處：情況2 里的導彈與目標作相向運動；而情況4 的導彈與目標卻是作背向運動，導致無法得到平行接近速率k的負實數解，平行接近策略失效。

通過以上4 種情況的仿真測試可知，當目標速度小于導彈速度時，不管導彈與目標的初始相對位置是何種情況，目標如何作機動，導彈均能按照平行接近策略擊中目標。但是，當目標速度大于導彈速度時，導彈能否擊中目標就與導彈與目標的初始相對位置以及初始相對運動關系息息相關，關鍵在于平行接近速率k是否存在負實數解。

8 結論

通過導彈與目標的位置關系和運動狀態，計算彈目平行接近速率，以不同情況分析平行接近速率是否存在負實數解。當存在負實數解時，意味著滿足采用平行接近策略的條件，導彈可擊中目標。得到平行接近速率后，計算得到導彈的期望彈道偏角和期望彈道傾角。運用反饋線性化方法，設計了導彈的期望彈道偏角速率和期望彈道傾角速率，經轉換得到導彈的縱向和橫向過載指令。該方法無須采用小量假設解耦俯仰、航向和滾轉三通道，直接設計了三維平行接近制導律，為平行接近策略的實現和現有比例導引法的改進提供了參考思路。最后，通過仿真測試，以不同情況的測試結果驗證了該方法的有效性。