基于模型與數據驅動的自適應模糊規則故障診斷方法

劉 路，史賢俊

（海軍航空大學，山東煙臺 264001）

0 引言

先進武器裝備的出現和發展反映了人類對產品性能和工程設計的進一步追求，這是先進智能裝備發展的必經過程[1]。故障診斷技術是實現安全有效工作的關鍵。近年來，國內外很多研究者都對故障診斷技術進行了比較深入的研究，多將故障診斷方法分成了兩種：一種是基于模型驅動的方法；另一種則是基于數據驅動的方法[2]。

基于模型驅動[3]的故障診斷技術有助于我們了解系統故障的存在原因，其對故障的因果關系表達清晰明了，具有自主、精確的診斷能力；但其對數學模型精確度或者經驗知識豐富程度依賴性較大，在復雜系統中的應用略受局限。基于數據驅動[4]的信息系統診斷方案是對全過程運行數據信息解析加工，并且不要求準確的數據分析建模就能夠實現對系統的診斷，但因為沒有系統內部結構和機理信息，難以解釋和理解。針對這一問題，本文提出了1 種利用診斷模型作為數據驅動方法的初始條件，進而提出1 種模糊規則自動更新機制，進一步提高了系統的故障診斷能力。

1 基于T-S故障樹的診斷模型

1.1 T-S故障樹的建造與事件描述

T-S故障樹是基于T-S建模的靜態故障樹，即根據T-S 建模構造T-S 門和它的描述規則來描述靜態事件關系和故障情況的1種新型靜態故障樹[5-6]。

T-S 故障樹由T-S 門和事件組成。事件包括頂事件、中間事件和基本事件[7]。圖1為典型的T-S故障樹結構。G1～G4為T-S 門，由T-S 模型的規則進行描述。y4為頂事件，y1～y3為中間事件，x1～x7為基本事件。對于y1門，x1～x3為下級事件，y1為上級事件；對于y4門，y2、y3、x7為下級事件，y4為上級事件。對于任一T-S門，它的輸出均為上級事件，輸入為下級事件。

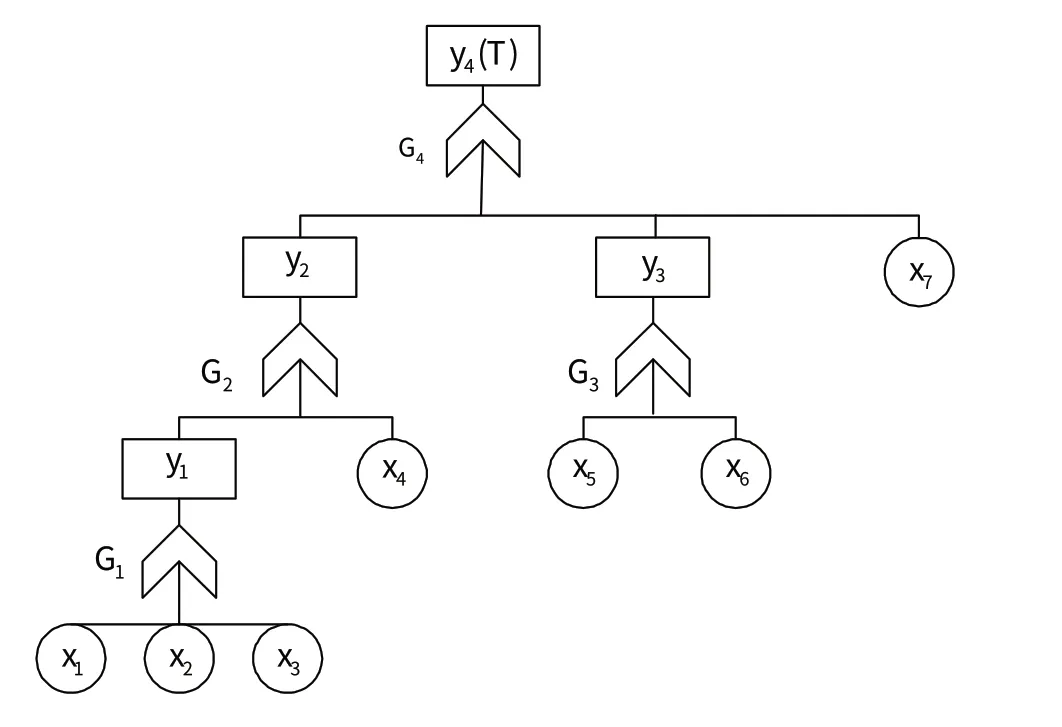
圖1 典型T-S故障樹結構Fig.1 Typical T-S fault tree structure

單元的故障狀況存在不確定性。本文利用模糊理論的隸屬度函數將模糊信息映射到[0，1]區間的某一精確值來表示故障狀態信息，選用如圖2 所示的四邊形隸屬函數來進行模糊語言的精確化[8]，其表達式如下：

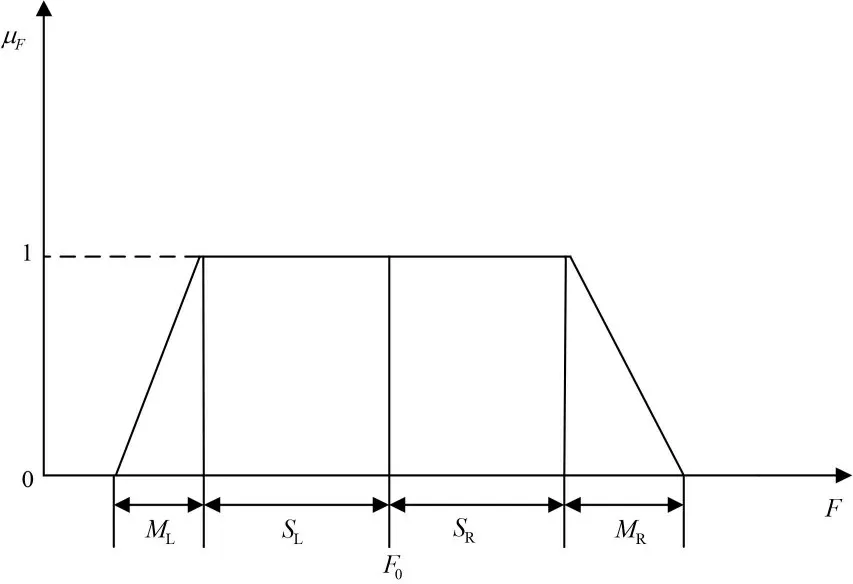
圖2 模糊數的隸屬度函數Fig.2 Membership function of fuzzy number

F0為模糊數支撐集的中心；SL為左支撐半徑范圍；SR為右支撐半徑范圍；ML為左模糊區；MR為右模糊區。模糊數F0用隸屬函數F來表示，其隸屬函數如下：

為了簡便表示故障情況，使用四邊形隸屬度函數模糊數來加以說明，同時也能保持其一般性。當SL=SR=0 時，四邊形隸屬度函數變成了三角形隸屬函數；當SL=SR=0 且ML=MR=0 時，模糊數也就變成了確定數；如果模糊數的隸屬函數左右相等，即左右對稱時，則SL=SR，ML=MR，左右支撐半徑SL和SR可為定值，也可為變量[9]。

1.2 T-S門描述規則

T-S門是根據T-S模型而建立的，是1種萬能逼近器，任何1種靜態事件的關系都可以分別由T-S門和1組IF-THEN規則來表示。而每1個T-S門的描述規則都包含了下級事件故障狀況所構成的輸入規則，以及對應于發生這些故障狀況時上級事件發生可能性所構成的輸出規則[10]。

T-S門的描述規則如表1所示。

表1 T-S門描述規則Tab.1 T-S gate description rules

在建立T-S故障樹的基礎上，用T-S門描述規則表征事件之間的邏輯關系，提高了診斷模型的精度，保證了故障樹分析的細粒度[11]，尤其是在處理多態信息、模糊信息和事件關系不確定性等方面具有顯著優勢。

2 模糊神經網絡故障診斷模型

2.1 模糊神經網絡模型的構造

考慮到模糊神經網絡的輸入輸出以及中間神經元的個數及代表的含義需要準確反映系統故障特征，確定較為困難，本文利用T-S 故障樹診斷模型完成對模糊神經網絡模型的建立[12-14]。網絡結構如圖3所示。

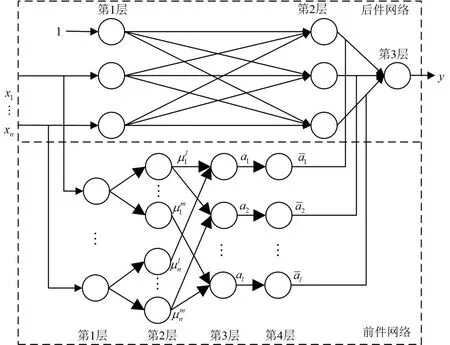
圖3 模糊神經網絡結構Fig.3 Fuzzy neural network structure

2.1.1 前件網絡

第1 層為輸入層，輸入變量的個數及含義由T-S故障樹中表征故障原因的基本事件確定，表征了根據故障原因采集故障樣本數據，并建立樣本矩陣作為網絡的輸入。

第2 層為語言節點層，使用隸屬度函數將輸入變量模糊化。在本層中，每個輸入變量的故障狀態模糊表達都由T-S 故障樹中的基本事件模糊數確定，從而確定了本層節點的個數及含義。

采用高斯函數來表達每個語言節點的隸屬度函數值，表達式如下：

2.1.2 后件網絡

第1 層為輸入層。其中，第0 個節點的輸入值x0=1，它為模糊規則后件提供常數項。

第2層為模糊規則計算。每1個神經元都表示了1種模糊規則。模糊規則如下：

第3 層為故障狀況的輸出層，即模糊神經網絡系統的輸出。本層神經元的數量及含義由T-S故障樹中表征故障模式的中間事件來確定，表征了故障診斷的目標是診斷到故障模式級別，計算公式如下：

式（7）中：ys為模糊神經網絡的輸出；ωsk為第k個歸一化規則節點與第s個輸出神經元間的連接權值；t為輸出神經元的數量。

綜上，建立了利用T-S 故障樹診斷模型作為模糊神經網絡數據驅動方法的初始條件來輔助網絡模型構建和學習的方法。

2.2 模糊神經網絡的學習算法

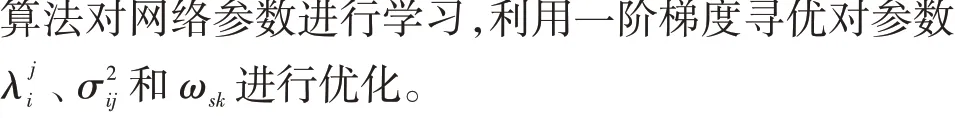
將采集到的故障樣本信息作為訓練樣本，可以假定FNN 的預期輸出值為Fsm，實際輸出值為Tsm，s=1,2,…,t,m=1,2,…,n，其中，t為輸出神經元的個數，n為樣本數量。定義尋優的誤差代價函數如下：

式（8）中：Ts,m為第m個樣本的第s個實際輸出值；Fsm為期望的輸出值。

首先，計算各個參數的梯度值，計算表達式如下：

2.3 模糊規則的自動更新

故障樣本信息輸入到FNN中后，在前件網絡的第2層進行對各自隸屬度函數值的運算。各個輸入量分別可以得到“故障”“可能故障”“正常”3種狀態的模糊表達值；然后，以最大隸屬度值作為輸出量傳遞至第3層，此時各個輸出所對應的規則節點均被激活，該節點與輸出相對應的計數器加1。各個規則的最大規則度計算表達式為：

假設FNN 有n個輸入，這些輸入都可用“故障”“可能故障”“正常”3個語義值來表示，第2層神經元的個數則為3n個。如果第3 層每1 個規則節點都被激活，那么規則數就有3n個；如果第3 層中有許多節點沒有被激活，那么這些規則將不存在。所以根據實際問題，獲得相對應的規則數，同時刪掉未被激活的節點，以簡化網絡的結構。假設每條規則出現的概率為p，p值越大，說明這條規則的重要程度越大。在FNN的訓練過程中，通過對得到的p值按降序排列，來選擇規則節點。

在FNN的學習訓練過程中，須不斷檢查測試模糊規則的最新狀況[16]。如果規則發生了變化，就使用動態篩選的方式及時加以更新，算法流程如圖4 所示。首先，對初始網絡設定學習次數并進行對網絡的訓練；然后，獲取新的初始規則，如規則沒有發生改變，則接著對網絡完成相應次數的學習，并確定規則不再改變；接著訓練網絡至推理誤差滿足期望的程度要求，若規則出現了變化，則首先記錄已存在的規則點的p值，并計算新生成規則的p值；最后，訓練網絡直到規則不再改變，從而確定規則并計算推理誤差。

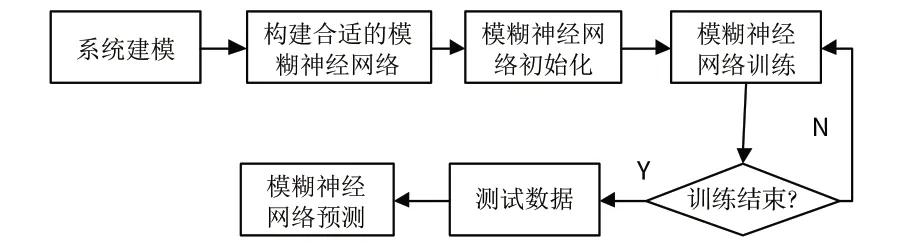
圖4 FNN算法流程Fig.4 FNN algorithm flow

3 實驗仿真及分析

3.1 組合導航系統TS-FNN構建

組合導航系統[17]是現代武器裝備中最重要的功能部件之一，主要用于實現對武器系統在飛行過程中相對于慣性空間的線性運動與角運動數據的即時檢測，并實時完成導航方程的運算，目前，其廣泛應用于軍工裝備、民用航空等各個領域。本文以某型裝備的組合導航系統為例來驗證所提出方法的有效性。

為解決系統元器件較多，系統T-S故障樹復雜、龐大的問題，根據系統信號連接關系和標定原理，將系統分解為6個輸出通道的故障。各通道之間存在很大相似性，因而選擇加速度計Ax的X通道為例，以“加速度計Ax的X通道故障”作為頂事件建立T-S 故障樹，如圖5所示。

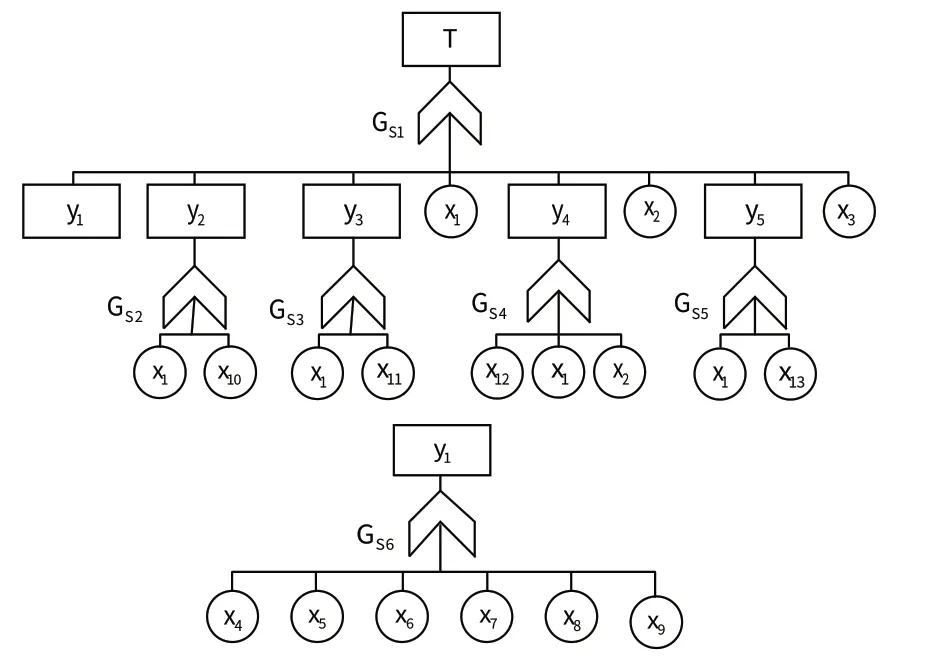
圖5 加速度計Ax 的X 通道故障T-S模糊故障模型Fig.5 Fuzzy fault model of X-channel fault T-S for accelerometer Ax

定義有模/數轉換電路板等5 個中間事件，如表2所示。定義回路電源板的+15V產生電路等13個底事件，如表3所示。

表2 中間事件定義Tab.2 Definition of intermediate events

表3 底事件定義Tab.3 Definition of bottom event

假設x1～x13和y1～y5的故障狀態為[0，0.5，1]，其中，0 表示正常狀態，0.5 表示半故障狀態，1 表示故障狀態。結合圖2 所示的四邊形隸屬度函數，參數選取為SL=SR=0.1，ML=MR=0.3。根據經驗和專家知識可以確定T-S模糊門GS1～GS6的描述規則[8]。以GS2門為例，描述規則如表4所示。

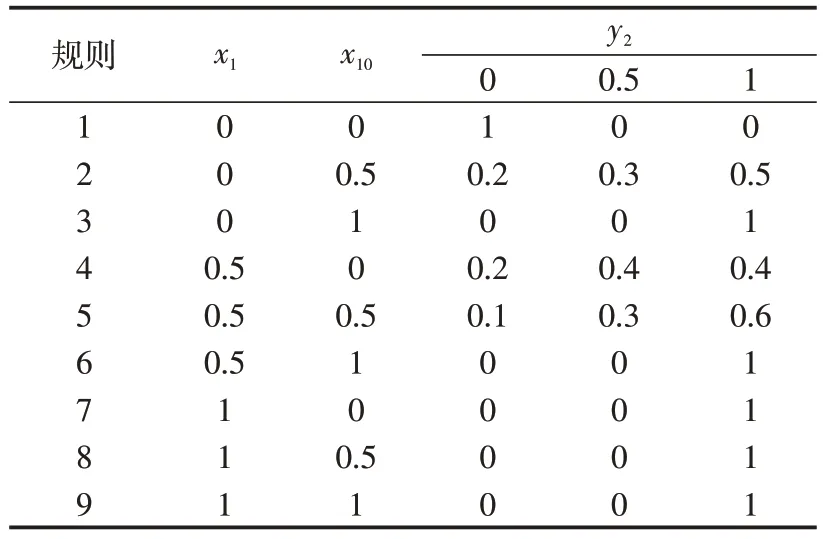
表4 GS2 門的描述規則Tab.4 Description rules of GS2 gate

表4中，每1行都代表1條模糊規則。規則2可解釋為：當x1回路電源板的+15 V產生電路正常且x10頻率標準板的1 kHz脈沖信號產生電路為可能故障狀態時，y2頻率標準板送到模/數轉換電路板的1 kHz脈沖信號正常狀態可能性為0.2，半故障狀態可能性為0.3，故障狀態可能性為0.5。

根據建立好的T-S 故障樹模型，映射得到FNN 的結構，確定了13種故障原因采集的故障樣本數據作為網絡的輸入，即x1～x13，每個輸入參數都對應有“偏高（H）”“正常（N）”和“偏低（L）”3 個模糊集合。中間事件對應網絡故障輸出為α1～α5，對應5種故障模式編碼，如表5所示，至此完成TS-FNN的構建。

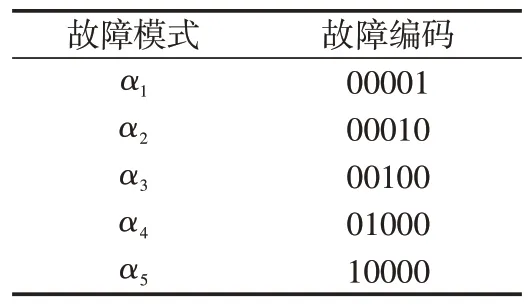
表5 故障模式對應編碼Tab.5 Failure mode correspondence code

3.2 仿真實驗分析

在13 個故障原因各自對應的模糊集合中各取40個數據，即1 560個樣本數據，隨機選取訓練樣本1 200個，測試樣本360個，設定網絡訓練次數為200次。為了對比訓練算法的收斂性能，采用傳統的PSO算法來進行比較。

圖6為傳統PSO算法和誤差反向傳播算法分別優化的TS-FNN模型訓練誤差隨迭代次數的收斂曲線對比圖，可看出：誤差反向傳播算法[18]在迭代40 次后得以收斂；而傳統的PSO算法優化的網絡模型則要80次后才收斂。由此可見，誤差反向傳播算法按梯度下降收斂的速度更快。

圖6 訓練誤差隨迭代次數變化的對比圖Fig.6 Comparison of training error with number of iterations

FNN 有13 個輸入，與之對應的規則有313條。通過設置規則索引，設定規則的激活閾值為0.05，如果規則被激活，那么與之對應的計數器加1；然后，計算出此規則節點的出現概率p，若p>0.3，則認為該規則為有效規則。每1條規則的激活概率如圖7所示。

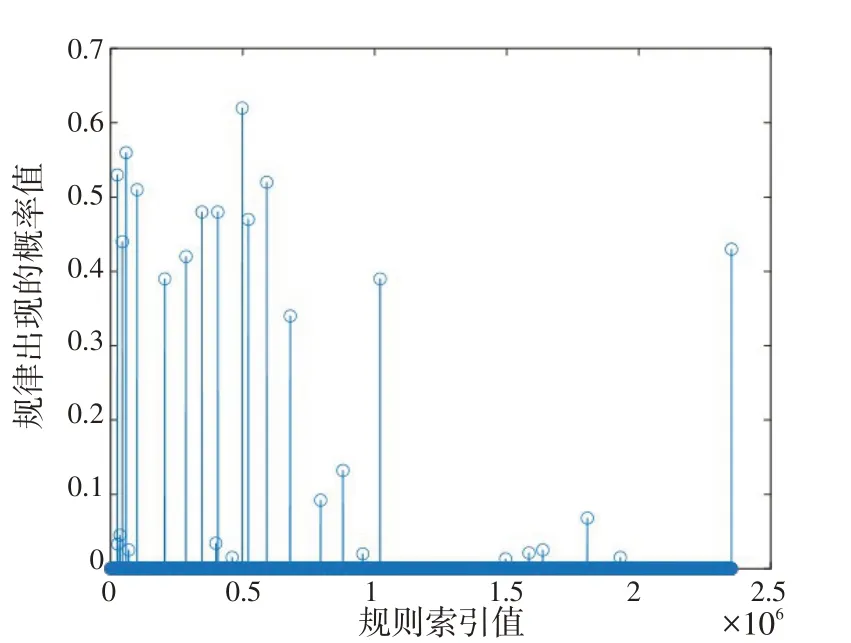
圖7 每條規則的激活概率Fig.7 Activation probability of each rule

圖7 中，共有14 條規則被激活，這些規則作為模糊神經網絡規則庫中的一部分，實現了對輸入數據的推理。

在仿真實驗中，將訓練好的參數凍結，再選取360個測試樣本用于網絡的測試，并記錄下測試的誤差，如表6所示。根據誤差反向傳播算法訓練得到的測試樣本診斷結果表明，本文設計的TS-FNN 能準確隔離出故障。

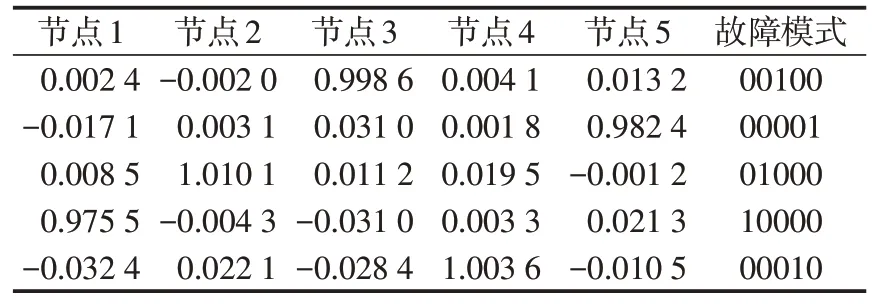
表6 TS-FNN的輸出結果Tab.6 Output results of TS-FNN

如表7 所示，基于誤差反向傳播算法得到的網絡模型隔離故障平均誤差為0.040 3，比傳統PSO算法降低了46.1%，說明本文提出的TS-FNN 具有較好的泛化能力。

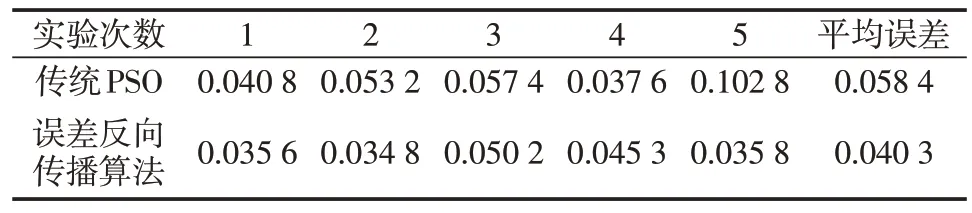
表7 故障隔離的誤差結果Tab.7 Error results of fault isolation

4 結論

本文基于T-S 故障樹理論分析，建立了系統各故障模式之間的邏輯關系和描述規則。并以此作為FNN 數據驅動方法的初始條件來輔助網絡模型構建和學習。構建的模糊規則的自動獲取與動態篩選的方法，能夠不斷地針對樣本狀況調整規則，大大增強了模型的有效性。將其應用于某型裝備的組合導航系統故障診斷中，實驗結果表明：本文提出的TS-FNN能夠準確診斷出故障，且具有較快的收斂速度和較好的泛化能力。