連續(xù)鋼箱梁橋頂推施工主梁線形修正方法研究

郝笛笛, 繆長青, 方詩圣

1.東南大學(xué)混凝土及預(yù)應(yīng)力混凝土結(jié)構(gòu)教育部重點(diǎn)實(shí)驗(yàn)室， 江蘇南京 210096；2.東南大學(xué)土木工程學(xué)院， 江蘇南京 211189；3.合肥工業(yè)大學(xué)土木與水利工程學(xué)院， 安徽合肥 230009

對(duì)于分階段施工鋼箱梁橋,無應(yīng)力線形控制精度是衡量成橋質(zhì)量的重要指標(biāo)[1-3],其線形控制可分解對(duì)梁段立面、平面與橫斷面的無應(yīng)力線形控制[4]。傳統(tǒng)頂推施工法中鋼箱梁無應(yīng)力線形匹配多以理論標(biāo)高進(jìn)行控制,梁段安裝時(shí)參照無應(yīng)力線形,這種直接以理論標(biāo)高為標(biāo)準(zhǔn)的線形控制方法包含了對(duì)預(yù)制梁段制造誤差的糾正,但難以解決已拼梁段梁軸線水平傾角的偏位問題[5]。采用頂推施工方法的鋼箱梁節(jié)段為異位拼裝,過程中伴隨結(jié)構(gòu)體系不斷轉(zhuǎn)化,線形偏位難以避免,如果不進(jìn)行及時(shí)修正,落梁后可能因梁體強(qiáng)迫位移產(chǎn)生較大殘余應(yīng)力,降低梁體的受力安全性[6]。

為此許多學(xué)者較早地針對(duì)如何實(shí)現(xiàn)分階段控制橋梁的無應(yīng)力線形問題,從理論方法和施工控制方面開展研究。秦順全[7]推導(dǎo)了分階段施工梁橋的過程狀態(tài)與成橋狀態(tài)的聯(lián)系,通過橋梁最終狀態(tài)的內(nèi)力與線形關(guān)系來求解施工中間狀態(tài)的內(nèi)力與線形。李傳習(xí)、董創(chuàng)文等[4,8]針對(duì)傳統(tǒng)頂推施工線形控制方法的不足相繼提出了“矩形法”、“帶直角梯形法”,通過調(diào)節(jié)梁段制造線形參數(shù)達(dá)到線形控制的目的。之后李傳習(xí)等[9]在分析了“矩形法”、“帶直角梯形法”的特點(diǎn)和適用性基礎(chǔ)上進(jìn)一步提出“等高等鄰邊法”,并結(jié)合“傳遞矩陣法”與“相位變換法”對(duì)拼接梁段進(jìn)行預(yù)測、控制及線形矯正。熊正強(qiáng)[10]采用“傳遞矩陣法”對(duì)頂推施工中各工況線形進(jìn)行預(yù)測和控制,并作了計(jì)算參數(shù)選取、線形狀態(tài)矩陣、偏位修正的理論研究,其線形控制理論在實(shí)際工程中得到應(yīng)用。周凌宇等[11]針對(duì)預(yù)制箱梁分階段拼裝提出了空間位置不重合坐標(biāo)系間轉(zhuǎn)換方法,減小了相鄰梁段在拼裝階段因整體與局部坐標(biāo)系轉(zhuǎn)換產(chǎn)生的拼裝偏位。但啟聯(lián)等[12]基于駐值原理推導(dǎo)了描述不同階段拼裝梁段最終線形與結(jié)構(gòu)剛度、外荷載及無應(yīng)力狀態(tài)量之間關(guān)系的控制方程,并借助其中參量進(jìn)行施工階段的線形控制。藺鵬臻等[13]借助有限元方法獲取了主梁拼裝階段吊索內(nèi)力與位移間的影響系數(shù),對(duì)柔性拱橋拼裝線形進(jìn)行動(dòng)態(tài)控制。

上述研究方法多清晰簡明,卻也有相應(yīng)局限,如“矩形法”、“帶直角梯形法”、“等高等鄰邊法”對(duì)梁段制造精度有較高要求,梁段制造誤差需要在拼裝過程中予以考慮和修正;“相位變換法”等對(duì)線形偏位的修正集中在少數(shù)梁段,未分析說明局部線形偏位對(duì)整體線形的影響,缺少較明確的評(píng)估指標(biāo)。“傳遞矩形法”在結(jié)構(gòu)分析與現(xiàn)代工程控制領(lǐng)域得到大量應(yīng)用[14-17],具有易理解和易實(shí)現(xiàn)編程等優(yōu)點(diǎn),由于頂推施工鋼箱梁橋采用異位拼裝方式,施工過程中實(shí)際線形偏位規(guī)律難以掌握,現(xiàn)有研究中采用的“傳遞矩陣法”主要為針對(duì)主梁豎向線形的控制,其遞推關(guān)系未考慮已拼裝梁段的水平向線形偏位和線形修正問題,李傳習(xí)、但啟聯(lián)等[9,12]已對(duì)該問題作出探討,仍缺少從整體結(jié)構(gòu)角度對(duì)已拼梁段線形偏位逐步修正方法及對(duì)已拼梁段無應(yīng)力線形的適時(shí)評(píng)價(jià)。

對(duì)于采用頂推法施工的連續(xù)鋼箱梁橋,已拼裝梁段的線形偏位不可逆轉(zhuǎn)[18],待拼梁段應(yīng)考慮主梁線形偏位修正。因此,及時(shí)、有效地評(píng)估實(shí)際線形偏位影響,是調(diào)整后續(xù)施工線形參數(shù)的重要步驟,也是實(shí)現(xiàn)高精度線形控制的重要環(huán)節(jié)。綜上,提出一種“線形偏位向量轉(zhuǎn)換法”,對(duì)理想狀態(tài)下的傳遞矩陣法進(jìn)行動(dòng)態(tài)修正。以拼裝完成的梁段上控制點(diǎn)實(shí)際偏位(相比設(shè)計(jì)線形)分布離散度作為評(píng)估指標(biāo),構(gòu)造相應(yīng)偏位向量及平方和表達(dá)式,通過求解偏微分方程極值,對(duì)已拼梁段線形進(jìn)行計(jì)算轉(zhuǎn)化,對(duì)鋼箱線形軸線水平向偏位與豎向偏位的階段性矯正。

1 線形控制理論

1.1 理想狀態(tài)下線形控制理論公式推導(dǎo)

對(duì)于分階段頂推施工鋼箱梁橋,一般按“以折代曲”的思路,將加工成直線型的梁段,采用含有角度的拼裝方式擬合設(shè)計(jì)線形[19]。首先,對(duì)理想狀態(tài)下線形控制理論公式進(jìn)行推導(dǎo),構(gòu)造如圖1所示坐標(biāo)系,以各拼裝鋼箱梁段中軸線兩端節(jié)點(diǎn)為控制點(diǎn),設(shè)Ki為梁段i尾端控制點(diǎn)編號(hào),坐標(biāo)為(Xi,Zi,Hi),Xi、Zi分別為平面順橋向、橫橋向水平坐標(biāo),Hi為高程,則梁段KiKi+1線形可由梁端控制點(diǎn)Ki、Ki+1坐標(biāo)確定。

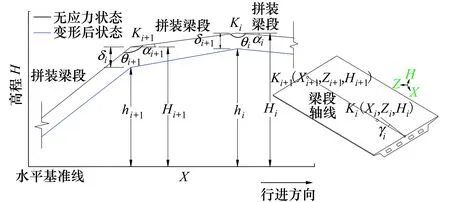
圖1 主梁無應(yīng)力狀態(tài)線形及變形后線形示意圖

拼裝平臺(tái)上的梁段線形可視為無應(yīng)力狀態(tài)線形[5,8],當(dāng)梁段遠(yuǎn)離拼裝平臺(tái)后,受自重、支承點(diǎn)變化、抄墊調(diào)整等綜合影響發(fā)生變形(主要表現(xiàn)為豎向撓曲),設(shè)變形后控制點(diǎn)Ki高程為hi,則理想狀態(tài)(無線形偏位)下有hi=Hi-δi,Hi,δi分別為該狀態(tài)下無應(yīng)力狀態(tài)線形對(duì)應(yīng)的高程和理論下?lián)献冃巍２环猎O(shè)某階段鋼箱梁無應(yīng)力狀態(tài)變形后的線形為梁段在此工況下的“理論線形”,則通過求得控制點(diǎn)變形δi,可得到鋼箱梁無應(yīng)力狀態(tài)線形下的控制點(diǎn)Ki坐標(biāo)。

已有研究表明,采用精細(xì)化有限元方法能夠以較高精度預(yù)測鋼箱梁控制點(diǎn)Ki下?lián)献冃桅膇[5],得到已拼裝梁段的“理論線形”。假定已拼裝梁段數(shù)為i,首段梁號(hào)為1,尾段梁號(hào)相應(yīng)為i,設(shè)該工況下控制點(diǎn)Ki狀態(tài)向量Vi={Hi,Xi,Zi,αi,θi,γi}T,其中Hi,Xi,Zi為控制點(diǎn)坐標(biāo),αi為實(shí)際梁段i軸線水平角,θi、γi分別為梁段i與待拼梁段i+1軸線豎向夾角與水平夾角,見圖2。

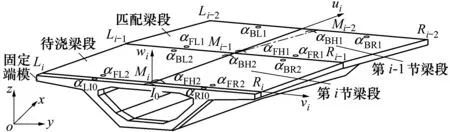
(整體坐標(biāo)系:o-xyz;局部坐標(biāo)系:Mi-uiviwi)圖2 整體與局部坐標(biāo)系示意圖[20]

此外設(shè)傳遞因子ki,ni,ji,滿足αi+1=kiαi,θi+1=niθi,γi+1=jiγi。其中ki、ni,ji可由鋼箱梁無應(yīng)力狀態(tài)線形與“理論線形”確定,有

(1)

式中,sin( )·ni=sinni,cos( )·ni=cosni,ni∈(αi,θi,γi),進(jìn)一步地,(1)式可表達(dá)為

Vi+1=KVi

K為狀態(tài)向量傳遞矩陣。通過以上相鄰控制點(diǎn)間的傳遞關(guān)系,可求得在“理論線形”下各工況中待拼梁段i+1中控制點(diǎn)Ki+1,即確定了控制點(diǎn)拼裝位置。

1.2 線形偏位評(píng)估與理論修正

1.2.1 線形偏位評(píng)估與偏位向量轉(zhuǎn)換

(1)式僅在無線形偏位時(shí)成立,對(duì)于頂推施工鋼箱梁橋,拼裝階段梁段實(shí)際線形與“理論線形”難以達(dá)到一致,因此考慮(1)式需要修正。工程中造成主梁線形偏位原因有多種,如梁段制造偏差、焊接溫度作用等,且偏位值往往具有隨機(jī)性和不穩(wěn)定性,但通過精密測量設(shè)備可實(shí)現(xiàn)對(duì)施工過程中主梁控制點(diǎn)坐標(biāo)及鋼箱梁間相對(duì)角度等關(guān)系數(shù)據(jù)進(jìn)行精確獲取,達(dá)到追蹤實(shí)際線形狀態(tài)的目的。

現(xiàn)有研究中對(duì)于梁段拼裝線形修正較多以調(diào)節(jié)相鄰數(shù)節(jié)待拼梁段線位來矯正主梁局部線形偏位[8],此類線形修正方式可能使得成橋階段不同梁段控制點(diǎn)高程偏位值呈現(xiàn)出較大離散性,造成落梁時(shí)主梁因強(qiáng)迫位移產(chǎn)生較大殘余應(yīng)力。因此,線形修正應(yīng)考慮局部線形偏位對(duì)整體線形控制的影響。

為能夠有效確定梁段空間坐標(biāo)信息并達(dá)到控制拼裝線形的目的,需定義合理的坐標(biāo)系統(tǒng)。周凌宇等[20]考慮了整體坐標(biāo)系和局部坐標(biāo)系空間位置不重合問題,將局部坐標(biāo)系中的誤差變換到整體坐標(biāo)系中,降低了局部坐標(biāo)系轉(zhuǎn)換誤差影響,見圖2。

對(duì)于采用整體和局部坐標(biāo)系轉(zhuǎn)換方法,每一拼裝階段均需要將待拼梁段局部坐標(biāo)轉(zhuǎn)換至整體坐標(biāo)系,當(dāng)梁段劃分較多時(shí),計(jì)算量隨之增加,同時(shí)拼裝誤差難以及時(shí)準(zhǔn)確地轉(zhuǎn)換至整體坐標(biāo)系中,易降低線形控制精度。由于坐標(biāo)系統(tǒng)的選取不影響主梁的空間線形狀態(tài),可將坐標(biāo)系原點(diǎn)設(shè)置于已拼裝梁段上,并通過相對(duì)坐標(biāo)關(guān)系得到主梁實(shí)際線形和偏位值分布。綜上,以行進(jìn)方向首段梁頭控制點(diǎn)K1為原點(diǎn),構(gòu)造笛卡爾三維坐標(biāo)系(見圖3)。設(shè)某一工況下已拼裝梁段數(shù)為i,梁段實(shí)際線形已知(通過控制點(diǎn)相對(duì)坐標(biāo)得到),分別構(gòu)造主梁軸線水平向偏位向量ez與軸線豎向偏位向量eh

因此,在該工況下,1～i節(jié)梁段實(shí)際線形與理論線形均為已知,以z,β,h,α為自由變量,根據(jù)幾何關(guān)系求得各控制點(diǎn)高程偏位zi,hi與z,β,h,α關(guān)系如(4)～(5)式所示

β-(m-1)π]},i≥1

(4)

α-(m-1)π]},i≥1

(5)

根據(jù)(4)～(5)式,分別構(gòu)造出已拼裝梁段控制點(diǎn)水平向偏位值平方和表達(dá)式R(γ,z)與豎向偏位值平方和表達(dá)式E(α,h)為

R(γ,z),E(α,h)均只含2個(gè)自由變量,根據(jù)數(shù)理統(tǒng)計(jì)理論,R(γ,z),E(α,h)值可反映該階段主梁實(shí)際軸線水平及豎向線形與理論線形擬合的優(yōu)良程度或離散度,當(dāng)R(γ,z),E(α,h)達(dá)到最小水平時(shí)整體線形偏位離散程度最弱,認(rèn)為整體線形控制最佳,且滿足控制方程

1.2.2 線形修正

(10)

修正后待拼梁段控制點(diǎn)Ki+1,Ki狀態(tài)向量傳遞關(guān)系為

Vi+1=KVi+Vc

(11)

計(jì)算得“轉(zhuǎn)換線形”后不需對(duì)實(shí)際梁段空間線形狀態(tài)進(jìn)行調(diào)整,僅通過待拼梁段控制點(diǎn)高程調(diào)節(jié),使其與現(xiàn)有梁段末節(jié)線位夾角與“轉(zhuǎn)換線形”一致即可。

2 工程應(yīng)用

2.1 背景介紹

合肥某跨高速連續(xù)鋼箱梁橋采用頂推法施工,主橋由140 m(40 m+60 m+40 m)三跨連續(xù)等高鋼箱梁構(gòu)成,鋼材等級(jí)Q345,箱梁為單箱四室斷面,腹板間呈封閉箱型,箱梁高2.6 m,上部寬19.40 m,下部寬12.56 m,橋面板為正交異性結(jié)構(gòu)。主梁豎曲線半徑為3 000 m,其起點(diǎn)坡度為-2.385%,終點(diǎn)坡度為2.462%;主梁橫坡為單向坡,坡度為2%。主橋與既有高速交角77°,如圖4所示。

鋼箱梁橋沿縱向分15節(jié)拼裝,頂推段為1～12節(jié),長度112.8 m;原位拼裝段為13～15節(jié),長度為27.2 m。頂推施工分6個(gè)施工階段,詳見表1,根據(jù)《公路橋涵施工技術(shù)規(guī)范》(JTG/T 3650-2020),鋼箱梁安裝后的線形允許偏差值見表2。

表1 不同施工階段工況內(nèi)容

表2 鋼箱梁安裝后允許偏差[21]

2.2 線形控制與實(shí)施效果

2.2.1 理論線形計(jì)算

為獲取較高精度的理論線形,結(jié)合鋼箱梁結(jié)構(gòu)特點(diǎn),基于ANSYS建立如圖5所示的鋼箱梁橋精細(xì)化三維板殼有限元模型(單元類型為4節(jié)點(diǎn)shell181,非縮減積分,材料采用雙線性隨動(dòng)硬化本構(gòu)),全模型單元數(shù)為102 209,節(jié)點(diǎn)數(shù)為150 701。計(jì)算考慮了重力與橋面施工荷載作用,同時(shí),在鋼箱梁支承點(diǎn)處建立彈性墊塊[22],避免因約束直接施加于模型節(jié)點(diǎn)而產(chǎn)生應(yīng)力集中現(xiàn)象,降低求解精度。利用生死單元技術(shù)實(shí)現(xiàn)不同階段鋼箱梁節(jié)段的拼裝與拆卸。

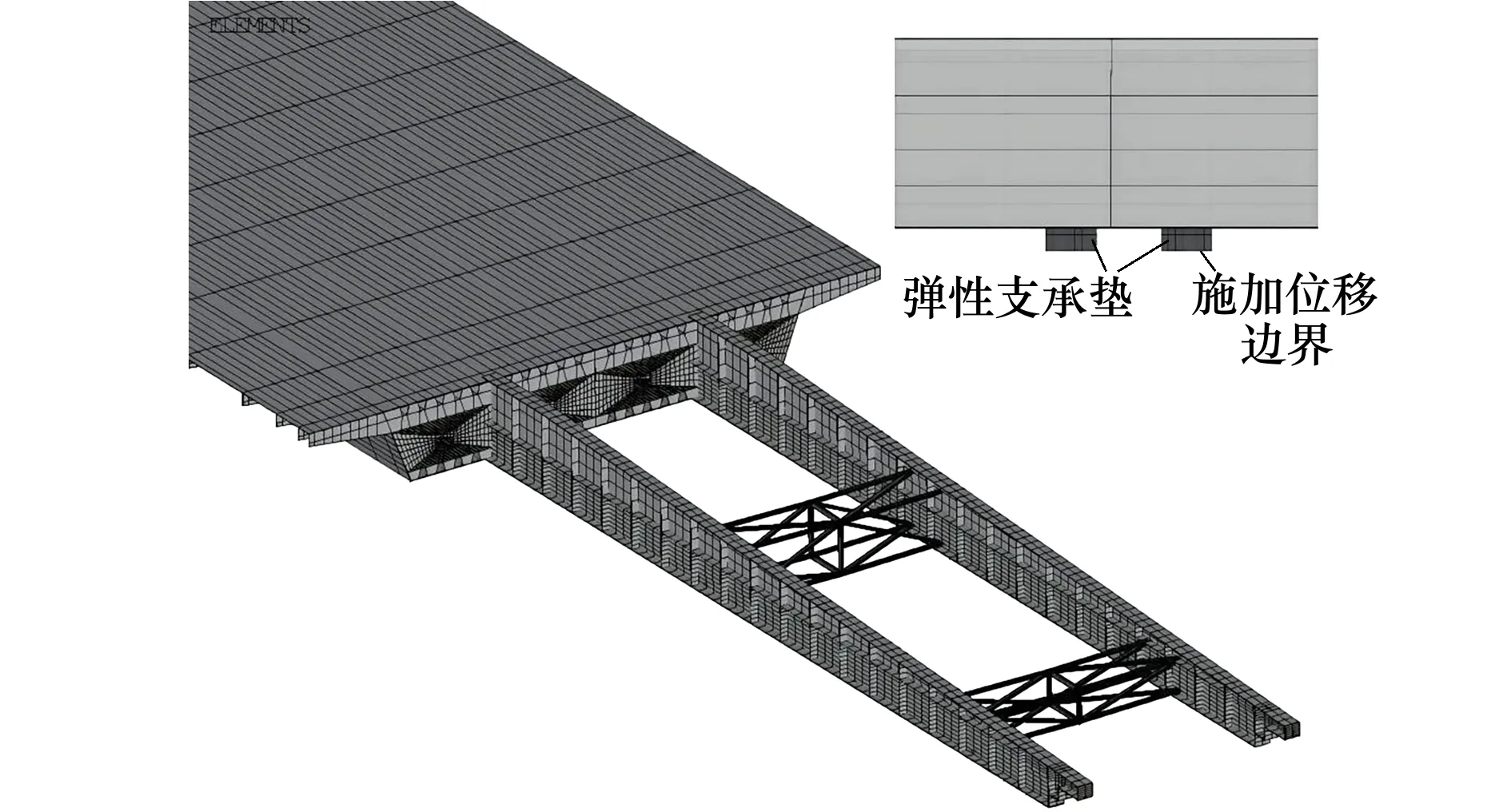
圖5 有限元模型

計(jì)算得各拼裝工況下遠(yuǎn)端梁段理論變形,如圖6所示。每一頂推階段到位時(shí),通過調(diào)節(jié)支架上抄墊塊高度,使支座力與計(jì)算得反力基本一致,實(shí)現(xiàn)主梁結(jié)構(gòu)與有限元計(jì)算數(shù)據(jù)的良好對(duì)接。

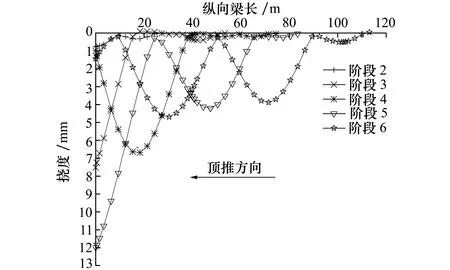
圖6 不同階段主梁下?lián)献冃吻€

2.2.2 監(jiān)控點(diǎn)布設(shè)

根據(jù)施工環(huán)境特點(diǎn),實(shí)際線形控制點(diǎn)選布于橋面,為能準(zhǔn)確測出主橋軸線豎向線形與水平線形,選擇地面參考坐標(biāo)點(diǎn)C1～C3,如圖7所示。

圖7 主橋平面監(jiān)控點(diǎn)布設(shè)示意圖

采用TrimbleS9全站儀,沿主梁縱向布設(shè)2條監(jiān)測線路,分別位于梁中軸線東、西側(cè),與梁中軸線水平距3.5 m,兩監(jiān)測線路對(duì)稱布置測點(diǎn),其中第5,11,15梁段布設(shè)2處測點(diǎn),其他梁段布設(shè)4處測點(diǎn)。各控制測點(diǎn)距拼接焊縫1 m,如圖8所示,全橋控制點(diǎn)測點(diǎn)共計(jì)42個(gè)。

圖8 主梁線形監(jiān)控點(diǎn)實(shí)物圖

2.2.3 線形控制效果

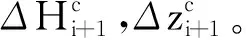
根據(jù)圖9～10監(jiān)測結(jié)果, 主梁軸線水平向偏位與軸線豎向偏位分布離散程度呈降低趨勢, 偏位值趨于穩(wěn)定、均勻化,階段性線形控制效果良好:第2～5階段頂推到位,軸線水平向偏位峰值分別為7.2,-4.8,5.4,4.7 mm;主梁縱軸線豎向線形偏位峰值分別為-26.3,26.3,17.3,-14.7 mm,線形偏位總體保持下降趨勢,相鄰階段最大偏位值降低9 mm。

圖9 各階段主梁軸線水平向偏位曲線

為進(jìn)一步驗(yàn)證提出的“線形偏位向量轉(zhuǎn)換方法”在頂推施工法中主梁線形控制的有效性,采用文獻(xiàn)[19]線形控制方法(未考慮局部偏位對(duì)整體線形影響的線形修正方法)對(duì)上述工程主橋線形進(jìn)行預(yù)測與控制。圖11～12分別為采用2種方法進(jìn)行線形控制時(shí)得到的第五階段主梁軸線水平向偏位與豎向偏位分布,表3為梁段理論匹配位置控制點(diǎn)坐標(biāo)數(shù)據(jù)。

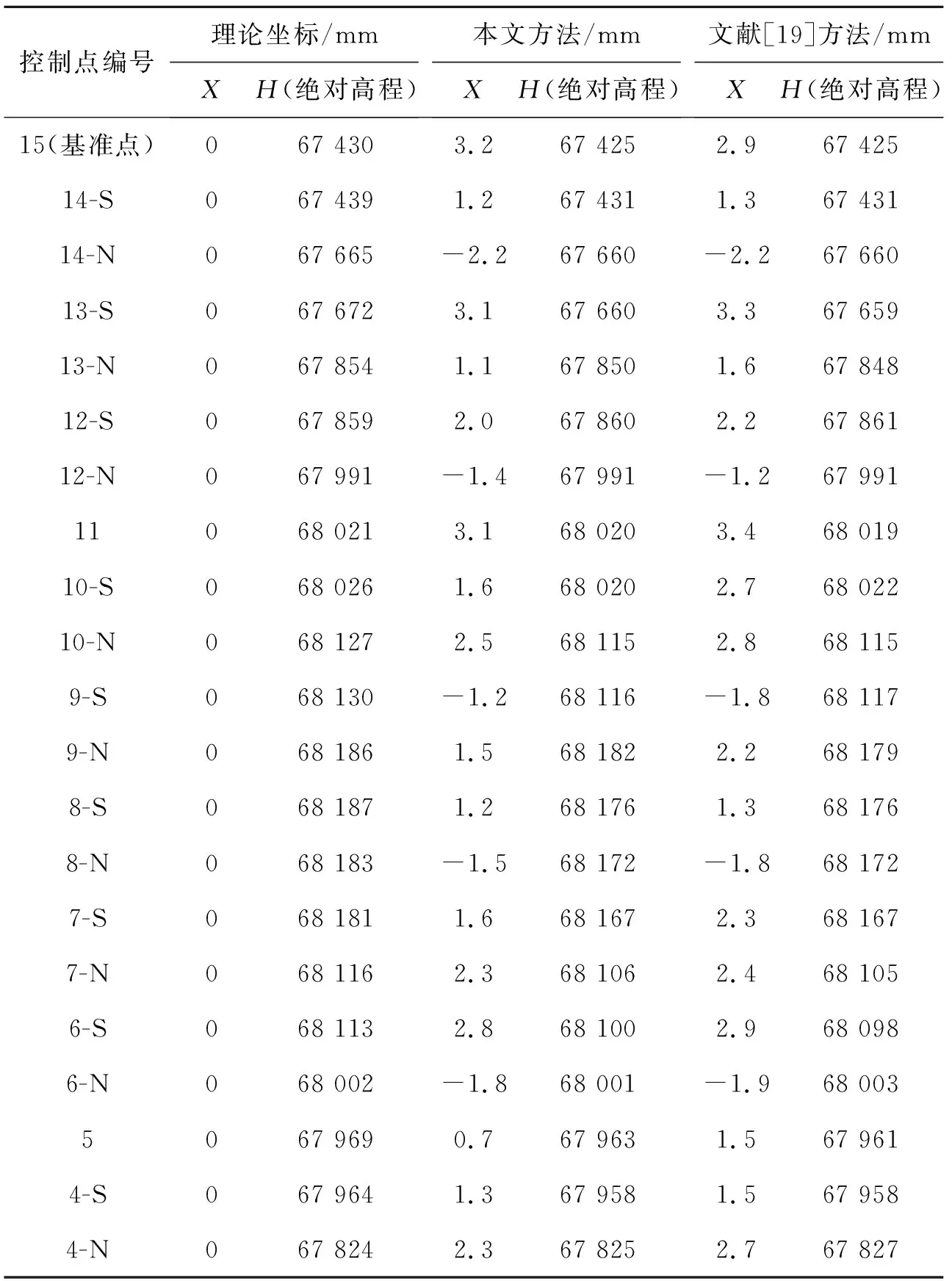
表3 梁段理論匹配位置控制點(diǎn)坐標(biāo)

結(jié)果顯示:主梁縱軸線各控制點(diǎn)水平偏位值均在±5 mm內(nèi),且2種方法下各控制點(diǎn)處水平偏位值相近,采用文獻(xiàn)[19]方法得到的主梁梁端處控制點(diǎn)水平偏位值較本文方法稍大;主梁軸線各控制點(diǎn)處豎向偏位值均在±15 mm內(nèi),其中采用本文提出的“線形偏位向量轉(zhuǎn)換方法”得到的主梁線形中各控制點(diǎn)豎向偏位值整體小1～2 mm,豎向偏位平方和為1 461.0,而采用文獻(xiàn)[19]方法得到主梁線形中的控制點(diǎn)偏位平方和為1 599.9,偏位值分布離散性更明顯。分析原因?yàn)?采用文獻(xiàn)[19]方法對(duì)待拼裝梁段線形進(jìn)行預(yù)測控制時(shí)未考慮局部線形偏位對(duì)整體線形的影響,使得成橋時(shí)主梁線形偏位分布更為離散,且偏位值較大。

如圖13,采用提出的“線形偏位向量轉(zhuǎn)換方法”對(duì)本工程主梁線形偏位進(jìn)行動(dòng)態(tài)修正,成橋時(shí)主梁軸線測點(diǎn)豎向偏位低于15 mm,水平偏位低于5 mm,永久墩處梁段控制點(diǎn)線形偏位低于10 mm,線形控制精度滿足規(guī)范要求。

圖13 成橋主梁軸線豎向線形

3 結(jié) 論

為提高頂推施工鋼箱梁橋主梁線形控制精度,提出一種“線形偏位向量轉(zhuǎn)換法”,對(duì)理想狀態(tài)下的傳遞矩陣法進(jìn)行修正,可實(shí)現(xiàn)對(duì)頂推施工中鋼箱梁線形偏位的階段性矯正,理論方法已在實(shí)際工程得到應(yīng)用。結(jié)論如下:

1) 本文推導(dǎo)了分節(jié)段拼裝鋼箱梁橋頂推施工中各梁段偏位值與變量偏位轉(zhuǎn)角及高度的表達(dá)式,構(gòu)建了衡量整體線形偏位程度的平方和公式,通過求解偏微分方程極值,求得整體線形偏位離散程度最小時(shí)的空間線形狀態(tài),得到理想狀態(tài)下的傳遞矩陣法的修正項(xiàng),改善了現(xiàn)有線形控制方法缺少從整體結(jié)構(gòu)角度對(duì)已拼梁段線形偏位逐步修正的不足之處。

2) 實(shí)際工程應(yīng)用表明,成橋時(shí)全頂推段主梁整體線形豎向偏位低于15 mm,軸線水平向偏位低于5 mm,永久墩處梁段線形豎向偏位與軸線水平向偏位分別低于10和4 mm,線形控制精度滿足規(guī)范要求。

3)“線形偏位向量轉(zhuǎn)換法”計(jì)算理論完整,易于編程,可針對(duì)不同施工環(huán)境對(duì)方法進(jìn)行調(diào)節(jié)轉(zhuǎn)換,為類似工程提供參考。