渦旋電磁波雷達平動旋轉目標三維微動參數提取方法

袁 航 何其芳 羅 迎* 王志浩 張 群

①(空軍工程大學信息與導航學院 西安 710077)

②(93114部隊 北京 100195)

1 引言

雷達目標在運動時往往伴隨著除質心平動以外的振動、轉動和加速運動[1-4]等微動(如直升機和旋翼無人機的旋翼轉動、炮彈彈丸在空中的自旋和進動等)。雷達與目標間的相對運動會對雷達回波產生多普勒調制，而由微動引起的多普勒調制稱為“微多普勒效應”[5-7]。微多普勒效應反映了目標的精細結構和運動特征，基于該效應能夠較好地分辨目標的屬性類型和運動意圖，為目標識別提供更多重要依據[8-10]。目標和雷達平臺的相對運動會在雷達回波中引起多普勒效應，該多普勒效應由目標整體平動和目標微動引起的多普勒效應組成。其中，將目標微動引起的多普勒效應稱為微多普勒效應。在傳統的單基平面電磁波雷達中，目標回波的微多普勒效應僅能反映目標三維運動投影到雷達徑向上的微動分量，基于傳統單基平面電磁波雷達的微動特征提取算法難以反演目標三維運動特征。而利用渦旋電磁波雷達、多基雷達或其他新體制雷達可以通過目標回波反演目標三維運動特征，因此為區別于雷達徑向微動分量，將此類反映目標三維運動特征的微動特征稱為三維微動特征[11,12]。

傳統平面電磁波雷達僅能觀測到目標投影到雷達徑向上的微動分量，當目標運動平面垂直于雷達徑向時，目標回波中將觀測不到微多普勒效應，導致基于微多普勒效應的目標識別方法失效[13]。同時，目標與雷達的相對姿態顯著影響目標投影到徑向上的微動分量大小，在特定的姿態角下不同尺寸的目標有可能產生相同的徑向微動分量，為識別帶來了困難[14,15]。以旋轉目標為例，傳統平面波雷達僅能估計目標徑向半徑和旋轉頻率，難以充分表征目標運動特征。渦旋電磁波相位波前分布為螺旋形，額外攜帶有軌道角動量(Orbital Angular Momentum,OAM)，不同軌道角動量的渦旋電磁波相互正交。利用渦旋電磁波照射微動目標，可觀測到目標投影到雷達徑向上的微動分量(引起“線多普勒效應(linear Doppler effect)”)和投影到垂直于雷達徑向的平面上的微動分量(引起“角多普勒效應(angular Doppler effect或rotational Doppler effect)”)，使得獲取目標的三維微動特征成為可能，雷達的信息獲取能力將顯著提高[16-18]。線多普勒和角多普勒之間的關系可用球坐標系下距離和方位角的關系描述，兩者為目標三維運動在距離域和方位角域的投影。線多普勒反映的是目標三維運動投影到雷達徑向上的微動分量，即目標運動引起的距離上的變化；角多普勒反映的是目標三維運動投影到垂直于雷達徑向平面上的微動分量，即目標運動引起的方位角上的變化。而球坐標系為正交坐標系，距離域和方位角域相互正交，因此雷達徑向上的微動分量和垂直于雷達徑向平面上的微動分量相互正交。

由于渦旋電磁波在目標微動特征提取方面的潛在優勢，近年來研究人員針對無平動旋轉目標微多普勒效應進行研究，探討了無平動旋轉目標角多普勒模型表征問題、線多普勒信號和角多普勒信號分離問題、目標微動參數提取問題等，取得了一系列成果。文獻[19]提出了無平動旋轉目標的角多普勒模型，探討了特殊情況下的角多普勒性質和微動參數提取方法，揭示了渦旋電磁波雷達在微動辨識領域的獨特優勢。文獻[20]對一般情況下的無平動旋轉目標角多普勒效應進行研究，利用近似角多普勒方程獲得角多普勒極值點，并利用壓縮感知算法獲得了微動參數的估計值。文獻[21]將雙模態的回波變換到時頻域，利用時頻圖像提取多普勒頻移曲線，通過計算雙模態回波間的頻移差值獲得角多普勒頻移曲線，并利用Hough變換估計無平動旋轉目標微動參數。

然而，現有渦旋電磁波雷達微多普勒效應研究主要針對無平動旋轉目標，并未考慮目標平動對角多普勒的影響。目標平動會在線多普勒中引入關于時間的多次項，這可以通過補償的方法去除；但與線多普勒不同，平動會使角多普勒發生顯著變化，無法簡單通過補償方法消除平動帶來的影響。若要將渦旋電磁波雷達應用于平動旋轉目標微動參數提取領域，需要進一步分析平動旋轉目標微多普勒效應的性質，有針對性地提出新的方法來解決該問題。因此，本文針對渦旋電磁波雷達平動旋轉目標微多普勒效應進行了研究，構建了平動旋轉目標運動模型，分析了目標平動對微動參數提取帶來的影響，討論了平動旋轉目標的角多普勒性質，最后利用L-M (Levenberg-Marquardt)方法[22]求解多元非線性方程組，基于1/4微動周期多普勒頻移曲線的時頻曲線，獲得了目標旋轉頻率、旋轉半徑、旋轉矢量、平動速度矢量等參數。仿真實驗驗證了角多普勒性質的正確性和參數提取方法的有效性。

2 渦旋電磁波雷達平動旋轉目標回波模型

為描述平動旋轉目標相對于雷達的空間三維運動，需要建立雷達坐標系、參考坐標系和目標本地坐標系，其中雷達坐標系的原點為雷達平臺，目標運動不改變雷達坐標系；目標本地坐標系以目標質心為坐標原點，隨目標運動而改變；參考坐標系用于構建目標本地坐標系與雷達坐標系之間的轉換關系，并表示目標從某固定姿態到實際姿態的變化。平動旋轉目標的觀測模型如圖1所示，均勻圓環陣列雷達用于產生渦旋電磁波，其中心為雷達坐標系OXY Z的原點O，陣列半徑為a，第k個陣元的坐標為(acos?k,asin?k,0)。參考坐標系ObXbYbZb的原點為Ob，雷達坐標系按照矢量R0平移后變為參考坐標系，參考坐標系平行于雷達坐標系。令散射點p以旋轉角頻率wb、旋轉半徑rb繞Ob旋轉，旋轉平面平行于圓環陣列。則在參考坐標系ObXbYbZb下，散射點p旋轉過程的坐標變化可寫為

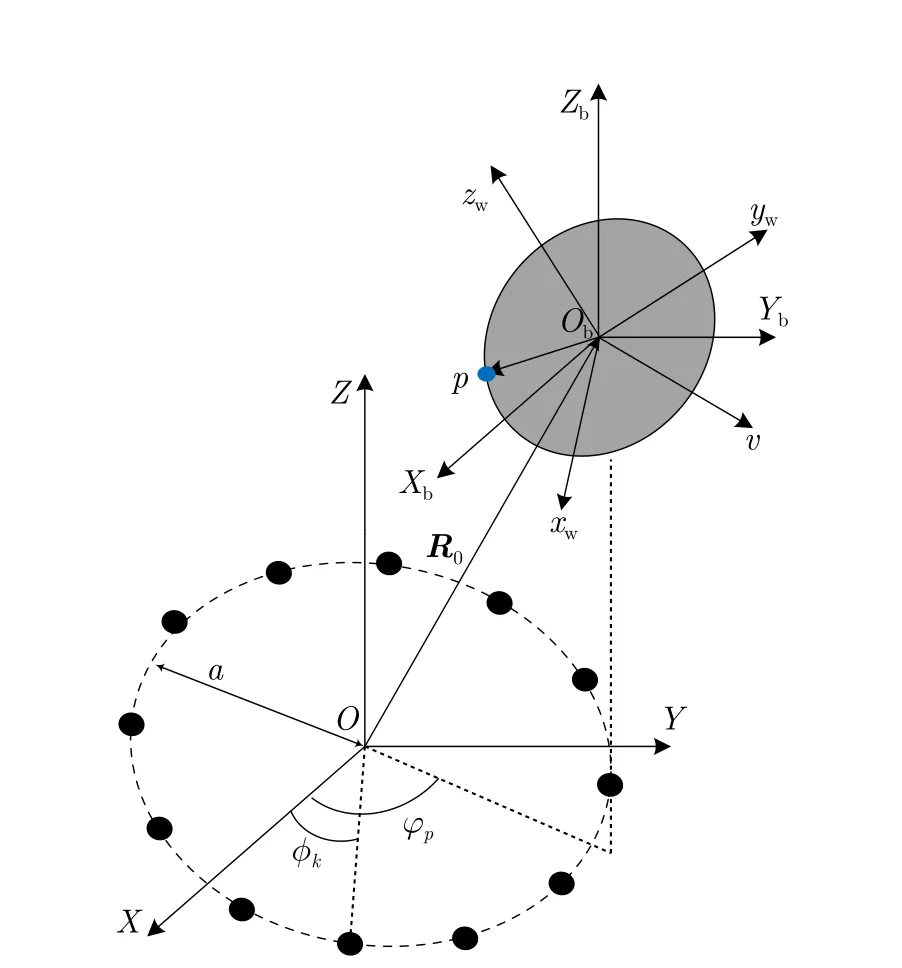
圖1 平動旋轉目標觀測模型Fig.1 Observation model of translational rotating targets

其中，()T為轉置操作，t為時間。進一步考慮將散射點的運動隨著參考坐標系經三維旋轉后變為目標本地坐標系Obxwywzw，變換過程可由一個三維變換矩陣表示。令由參考坐標系旋轉到目標本地坐標系的旋轉矩陣的歐拉角為 (θ1,θ2,θ3)，則旋轉矩陣Ri可表示為

隨后目標以速度矢量v=(vx,vy,vz)T整體平動，雷達坐標系原點O指向散射點p的矢量可寫為

三維旋轉會改變散射點p的旋轉平面投影到雷達坐標系上的變化幅度和初相。但對于旋轉目標，三維旋轉中繞軸ObZb的旋轉僅改變初相，對分析并無影響。因此可忽略繞軸ObZb的旋轉，將目標的三維旋轉簡化為繞軸ObYb和軸ObXb的旋轉。此時三維旋轉矩陣可寫為

同時，根據三維旋轉矩陣易知旋轉目標的旋轉矢量為(sinθ2,-sinθ1cosθ2,cosθ1cosθ2)T。

一個旋轉半徑為0.4 m、旋轉中心為(0.8,1,300) m，歐拉角為(1.04,0.78,0.62) rad的旋轉目標的距離和方位角變化過程如圖2所示。圖2(a)和圖2(b)為根據式(2)和式(4)所示的旋轉矩陣生成的目標距離和方位角變化過程。圖2(a)中兩者的距離變化幅度相同，時間相差約0.01 s，證明了簡化后的旋轉矩陣在距離上的有效性。圖2(b)中兩者方位角變化幅度相同，時間同樣相差約0.01 s，證明了簡化后的旋轉矩陣在方位角上的有效性。因此，可以將三維旋轉矩陣簡化為式(4)所示的形式，以簡化分析和求解難度。

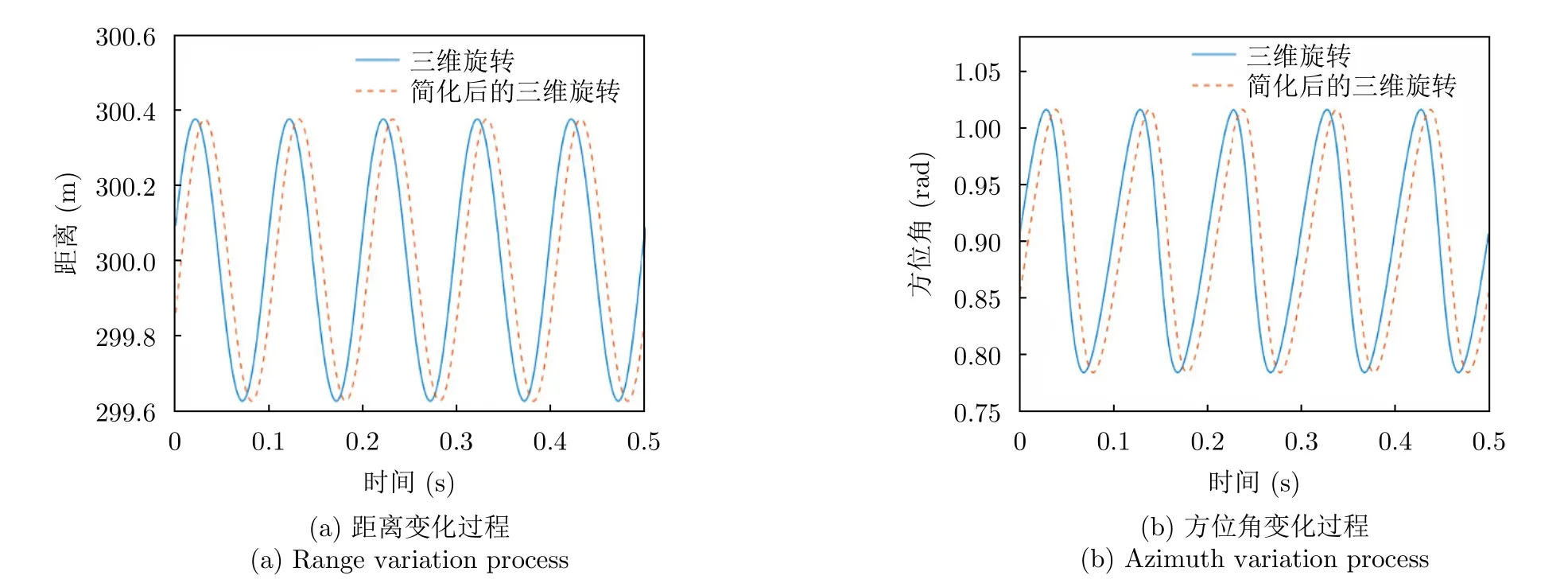
圖2 三維旋轉結果Fig.2 The three-dimensional rotation result

根據簡化后的三維旋轉矩陣，雷達坐標系原點O指向散射點p的矢量可寫為

arctan()為反正切函數。則散射點p在球坐標系下的坐標(rp(t),θp(t),φp(t))T可寫為

其中，arcsin()為反正弦函數。天線中心發射單頻信號 exp(i2πfct)照射到目標上，圓環陣列上多個添加了固定相移的陣元接收回波，將回波合成，散射點p的渦旋電磁波雷達回波可寫為[17]

3 微多普勒效應分析及微動參數提取

目標距離變化在渦旋電磁波雷達回波中引起線多普勒效應，方位角變化在回波中引起角多普勒效應，線多普勒和角多普勒結合為渦旋電磁波雷達回波微多普勒效應。當前已有研究提出了渦旋電磁波雷達線多普勒信號和角多普勒信號分離方法[21]，所以本節中分別對旋轉目標的線多普勒效應和角多普勒效應進行分析。

首先對平動旋轉目標的線多普勒效應進行分析。目標在空間中的勻速直線運動投影到徑向上，可近似將距離rp寫為

實際上渦旋電磁波雷達的波束指向通常較為接近Z軸，例如，當雷達波束指向為3°時，假設目標距離為r，zb=rcos 3?遠大于xb和yb。在該情況下，徑向半徑rbh3可近似為

目標平動使線多普勒頻移出現常數項和時間的一次項，但這兩項可以通過對頻移曲線進行補償或對頻移曲線求高階導數去除。目標微動分量對線多普勒的影響主要體現在第3項中，該項由旋轉中心坐標、旋轉半徑、歐拉角和旋轉角頻率共同決定。由于線多普勒頻移曲線以正弦規律變化，通過分析曲線的周期可提取目標旋轉頻率，但旋轉半徑和傾斜角相互調制，利用線多普勒僅能提取目標徑向半徑rbh3。

目標方位角的變化會引起回波中的角多普勒效應，由于方位角表現為反正切函數的形式，對方位角求導獲得的角多普勒頻移表達式較為復雜。方位角展開可寫為

分子和分母中含有初相不同的余弦函數，初相的存 在為角多普勒分析帶來了較大的影響。同時，分母多項式存在于反正切函數中，對反正切函數求導獲得目標角多普勒，進一步加劇了角多普勒方程的復雜程度。將式(14)代入式(8)中的角多普勒項并求導，獲得角多普勒頻移方程fa(t)

當速度矢量v=0時，式(15)退化為

式(16)即為無平動旋轉目標角多普勒頻移方程，式(16)的分子和分母中僅有三角函數項隨時間變化，而三角函數均為周期函數，所以式(16)表示的無平動旋轉目標角多普勒頻移呈現周期性。而式(15)中的分子和分母中與時間相關的項有3種：三角函數項、因速度矢量引起的一次項、一次項和三角函數的耦合項。其中三角函數周期性變化，后兩種并非周期函數，導致有平動時角多普勒頻移曲線周期性消失。與無平動旋轉目標相比，平動旋轉目標的角多普勒頻移方程更加復雜，需要考慮在不同情況下速度矢量對角多普勒的影響。

首先分析式(15)中分母對角多普勒曲線的影響。分母多項式的性質決定了當分母趨于0而分子不為0時，角多普勒必然會急劇增大。而式(15)的分母可視為在XOY平面上的一個橢圓。由于橢圓中心為(xb+vxt,yb+vyt)已知，為簡化推導橢圓方程的難度，先將式(15)所示的橢圓平移到原點，此時橢圓的一般式方程可寫為

根據橢圓的性質，式(17)所示的橢圓可通過某標準橢圓經二維旋轉獲得，該二維旋轉的角度θ為

基于二維旋轉角度并根據橢圓旋轉的性質，將橢圓中心設置為 (xb+vxt,yb+vyt)后，可獲得式(15)分母所示橢圓的標準化方程

隨著時間的變化，式(15)的分母可視為橢圓中心Od在平動的橢圓上一點q到原點的距離，點q隨時間變化過程如圖3所示，上文求得的二維旋轉角度θ體現為橢圓長軸與軸OX的夾角。

圖3 點q在平面X OY上的軌跡Fig.3 The trajectory of the point q on plane XOY

若點q恰巧經過坐標系原點O，則式(15)的分母為0，角多普勒趨于一個較大的值。設定旋轉中心為(1,1,600) m，旋轉半徑為0.4 m，旋轉頻率為10 Hz，速度矢量為(-11,375,-11.33,0) m，歐拉角為(0,0,0)rad。該情況下的角多普勒頻移曲線如圖4所示，圖中藍線為忽略速度矢量后根據式(16)生成的角多普勒頻移曲線，橙線為考慮目標平動情況下的角多普勒頻移曲線。

圖4 角多普勒頻移曲線Fig.4 Angular Doppler frequency shift curve

為便于分析速度矢量帶來的影響，設歐拉角θ1=θ2=0，目標旋轉平面平行于XOY平面。藍色角多普勒頻移曲線的旋轉中心為當wbt=5π/4時角多普勒曲線出現尖峰，此時角多普勒值為-4499 Hz。橙色角多普勒頻移曲線的旋轉中心為xb=yb=2.5rb，速度矢量為v=(-11.395,-11.46,0)Tm/s，通過設置特定的參數使橢圓中心平動到某位置時點q恰巧經過坐標系原點O，從而角多普勒出現較大的值。

與線多普勒不同，角多普勒對旋轉中心較為敏感，當旋轉中心和其余微動參數滿足一定關系時，角多普勒曲線特征明顯，能提供更多的目標信息。但要考慮角多普勒出現尖峰是因為點q恰巧經過坐標系原點O，實際上渦旋電磁波波束中心存在能量空洞，該情況在實際中難以出現。多數情況下，旋轉中心平動導致點q接近坐標系原點O，從而使角多普勒曲線產生波動，該情況下的角多普勒頻移曲線如圖5所示。旋轉中心接近原點O使角多普勒值顯著增大，橢圓與原點交錯時點q與O越接近，角多普勒最大值越大。橢圓與原點交錯后，橢圓中心遠離原點O，角多普勒曲線逐漸趨于0。需要指出，受限于渦旋電磁波雷達回波幅度中調制的貝塞爾函數的影響，當角多普勒頻率較大時(此時旋轉目標點接近渦旋電磁波中心空洞)回波能量較小，該時間段對應的角多普勒曲線的提取難度較大。但通過觀測時頻圖中曲線能量較低處，可以間接獲得角多普勒曲線尖峰處的位置。

圖5 多數情況下的角多普勒頻移曲線Fig.5 Angle Doppler curve in most cases

在分析分母對角多普勒曲線的影響后，需要考慮速度矢量方向對角多普勒頻移曲線的影響。根據速度矢量的方向和橢圓與原點O的相對關系，可分為4種情況：一是原點O在橢圓內，速度矢量使旋轉中心遠離雷達視線方向；二是原點O在橢圓外，速度矢量使旋轉中心遠離雷達視線方向；三是原點O在橢圓內，速度矢量使旋轉中心接近雷達視線方向；四是原點O在橢圓外，速度矢量使旋轉中心接近雷達視線方向。分別展示該情況下角多普勒頻移曲線，并對這4種情況進行討論，4種情況下的角多普勒頻移曲線如圖6所示。其中圖6(a)和圖6(c)的時頻曲線較為接近，其原因為在目標平動的過程中點接近原點的次數均為兩次，且穿過原點后旋轉中心遠離原點。圖6(b)為原點位于橢圓外部，點q未與原點接近，所以該情況下的時頻曲線并未出現尖峰。圖6(d)出現4個較大的角多普勒值，其原因為橢圓中心自遠處向原點平動，該情況下點q接近原點4次。可以發現點q與原點的相對位置直接決定了角多普勒頻移曲線的形狀，因此也可通過角多普勒頻移曲線的形狀初步判斷目標旋轉中心與原點的相對位置、速度矢量的方向，為下一步的參數提取提供一定的信息。

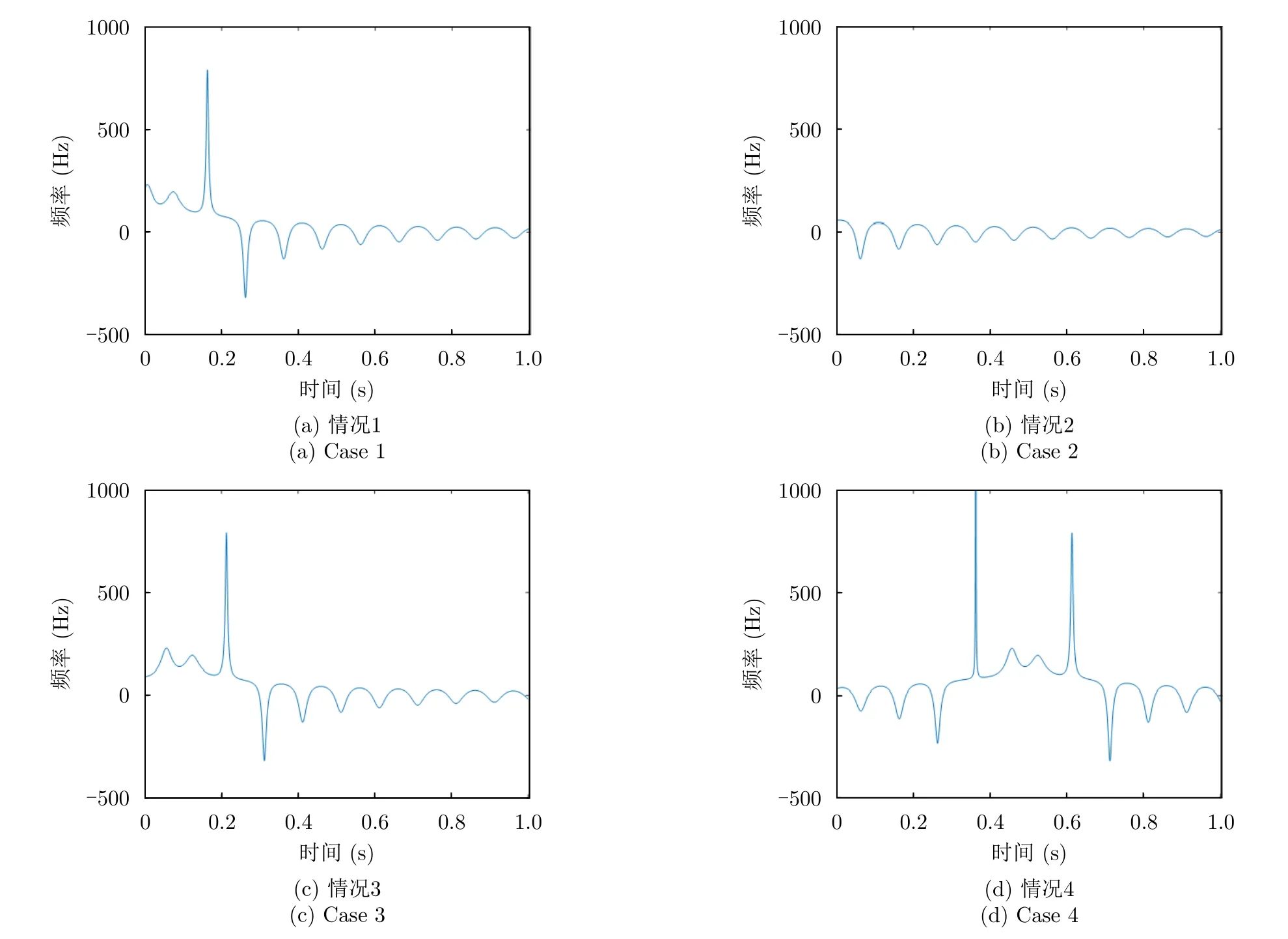
圖6 4種情況下的角多普勒頻移曲線Fig.6 Angle Doppler curve in four cases

在分析速度矢量對角多普勒曲線的影響后，需要考慮其余微動參數和角多普勒之間的聯系。首先對無平動旋轉目標角多普勒方程進行分析，進而拓展到平動旋轉目標角多普勒方程。將式(16)上下同時除以，則式(16)可重寫為

由式(22)可以發現，實際上旋轉半徑、旋轉中心坐標的絕對大小并不影響角多普勒曲線，旋轉中心坐標與旋轉半徑比值決定了角多普勒曲線的性質。

因此，可以得出無平動旋轉目標角多普勒的一個性質：角多普勒由旋轉半徑和旋轉中心坐標的相對大小決定，與這3個參數的絕對大小無關。參照無平動旋轉目標將式(15)上下同時除以，將式(15)重寫為

與式(22)類似，式(23)表示的角多普勒曲線同樣由微動參數(除歐拉角和旋轉頻率外)間的相對大小決定，該性質表明若僅用角多普勒曲線進行參數估計，僅能獲得旋轉角頻率、歐拉角和其余參數間的相對大小。

在分析平動旋轉目標角多普勒效應的基礎上，構建多元非線性方程組，利用L-M算法求解方程組，估計目標微動參數。線多普勒主要以正弦函數規律變化，從頻移曲線中能提取的信息較少。可以對線多普勒曲線求二次導數濾除速度項的影響，其結果為

可以發現每次求導都會使相同時間段下的線多普勒幅度值乘以旋轉角頻率，因此可通過對比二次導數和三次導數間的幅度差提取目標旋轉角頻率。

與線多普勒相比，角多普勒方程為分母多項式，時間會引起角多普勒的復雜變化，角多普勒頻移曲線中蘊含更多的目標微動信息。因此可以利用角多普勒曲線中的多個點構建多元非線性方程組，通過求解方程組估計目標微動參數。若通過線多普勒估計旋轉角頻率，則式(23)中含有6個未知參數，最少需要選取角多普勒曲線上的6個點構建方程組。由于角多普勒蘊含豐富的目標信息，可以利用較短周期的頻移曲線提取目標微動參數。實際上，頻移曲線長度首先影響基于線多普勒的旋轉角頻率和徑向半徑提取。旋轉角頻率可以通過對線多普勒頻移曲線高階導數間的幅度差值獲得，但在較短頻移曲線長度下無法估計徑向半徑。為從線多普勒頻移曲線中提取目標徑向半徑，最短需要1/4周期的頻移曲線以確保線多普勒極值被包含在周期內。設由角多普勒曲線獲得的第l個點的值為(l)，方程組可寫為

利用L-M算法求解方程(25)所示的多元非線性方程組，即可獲得微動參數估計值，其中旋轉角頻率和歐拉角的估計值為準確值，并可根據歐拉角計算目標旋轉矢量。但由于角多普勒本身的性質，獲得的旋轉半徑、旋轉中心坐標、速度矢量均為相對大小，需要聯立線多普勒獲得上述參數的絕對大小。

在獲得旋轉角頻率、歐拉角和微動參數間的相對大小的基礎上，只需將選取點之間的線多普勒二次導數差值代入式(24)即可獲得徑向半徑估計值rl

根據角多普勒已估計目標歐拉角θ1和θ2，所以根據式(26)可獲得旋轉半徑估計值。將旋轉半徑代入微動參數間的相對大小，即可獲得旋轉中心坐標、速度矢量的估計值。至此，綜合利用線多普勒和角多普勒，實現了對平動旋轉目標微動參數的提取，其處理流程如圖7所示。

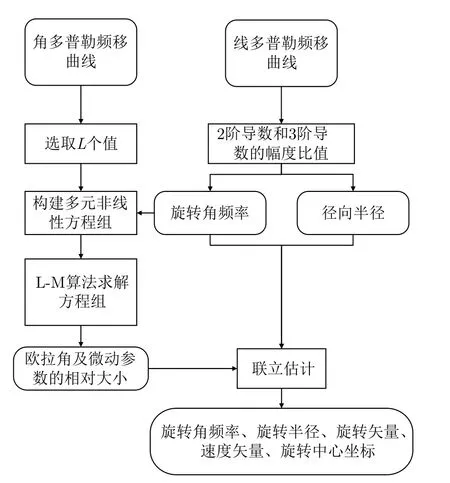
圖7 算法流程圖Fig.7 Algorithm flow chart

4 仿真結果

本節將驗證所推導的平動旋轉目標角多普勒性質，并驗證所提三維微動參數提取方法的有效性。

首先設定渦旋電磁波雷達參數和平動旋轉目標參數，雷達與目標參數如表1所示。

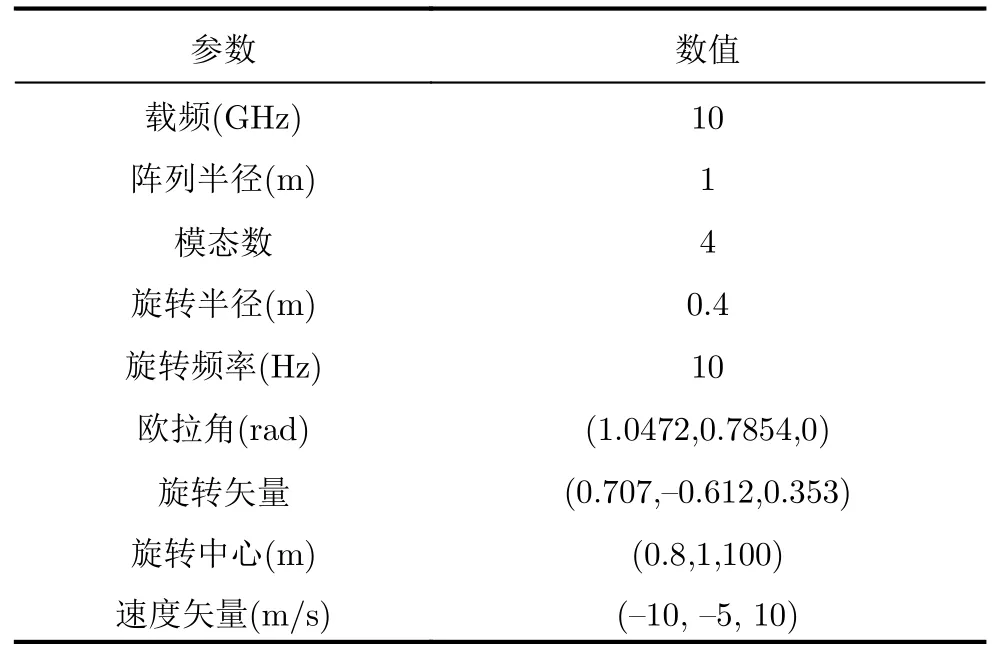
表1 雷達和目標參數Tab.1 Parameters of radar and target

根據目標運動模型生成對應回波，對相位求導獲得多普勒頻率的理想曲線。根據表1所示參數，目標理想多普勒曲線和根據式(11)和式(15)生成的多普勒曲線如圖8所示，圖8(a)和圖8(b)分別為線多普勒頻移曲線和角多普勒頻移曲線。圖8(a)中藍色曲線為理想線多普勒曲線，橙色曲線為根據式(11)生成的線多普勒曲線，兩個曲線基本重合，證明了式(11)的正確性。同樣，圖8(b)中藍色曲線為理想角多普勒曲線，橙色曲線為根據式(15)生成的角多普勒曲線，兩者的相似程度證明了式(15)的正確性。

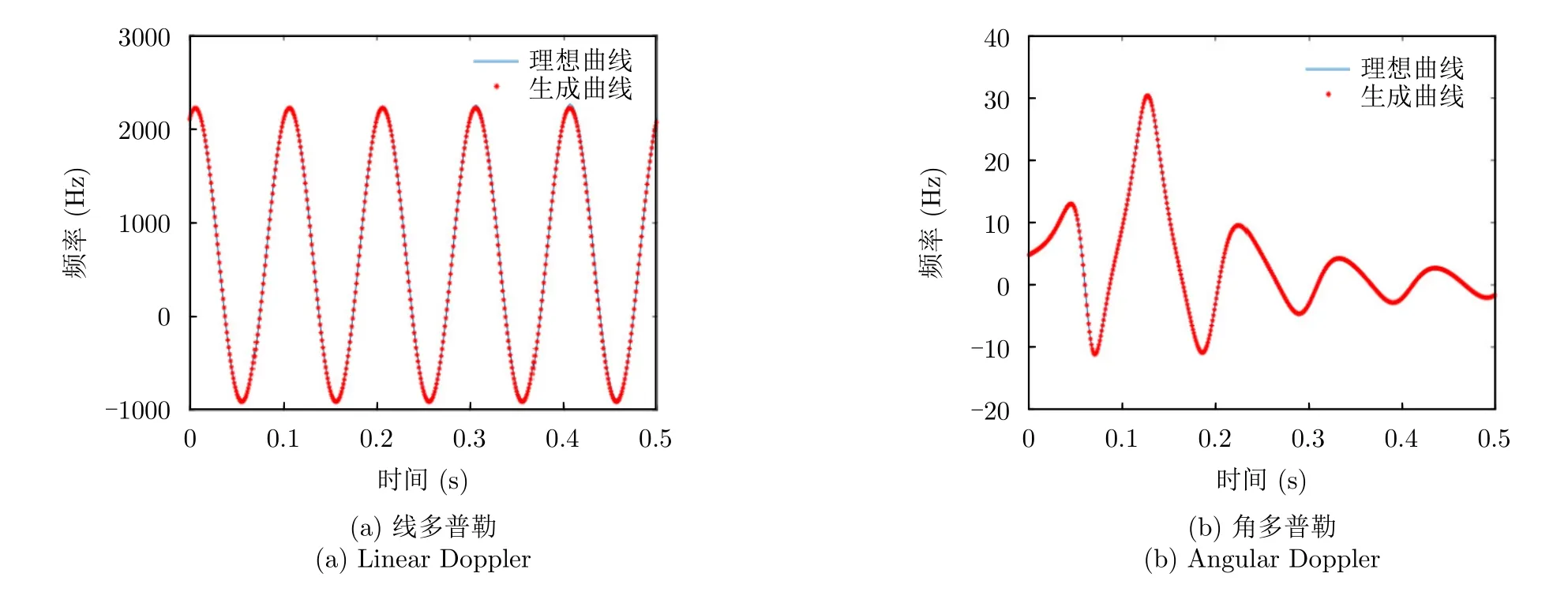
圖8 多普勒曲線Fig.8 The curve of Doppler

該情況下目標的俯仰角變化曲線如圖9(a)所示，由于目標的平動和旋轉，目標俯仰角在0.004～0.045 rad變化。該變化導致Bessel函數的值發生變化，其過程如圖9(b)所示。由于俯仰角的變化，不同時間段下的回波信噪比不同，導致了回波時頻圖中的能量分布隨時間改變，該情況下的回波時頻圖如圖10所示。在0.05～0.20 s左右的時間段，回波能量顯著減小，當基于時頻圖提取目標角多普勒曲線時，直接影響該段的角多普勒曲線提取精度。

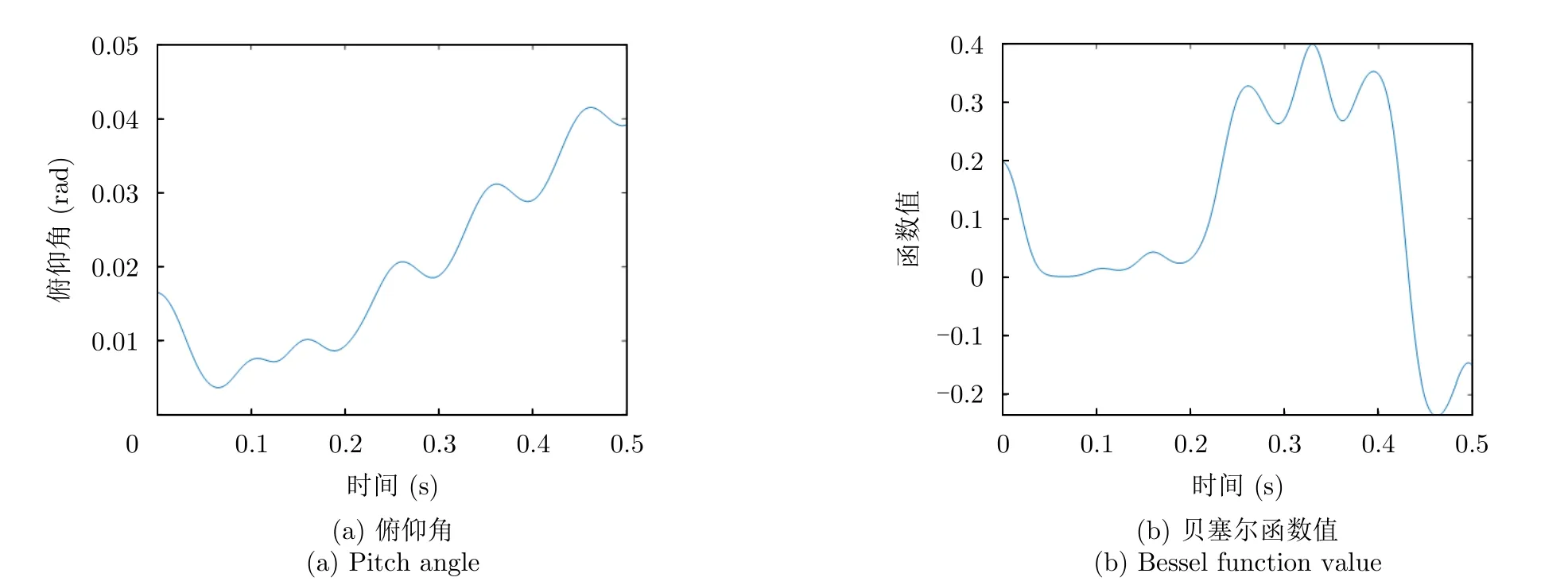
圖9 俯仰角及貝塞爾函數值變化曲線Fig.9 Pitch angle and Bessel function value change curve

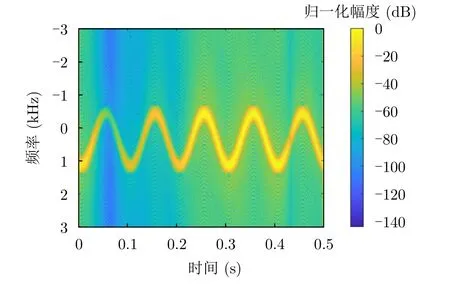
圖10 回波時頻圖(線多普勒＋角多普勒)Fig.10 Echo time-frequency map (linear Doppler+angular Doppler)

在證明式(11)和式(15)的正確性后，繼續驗證“角多普勒曲線由微動參數間(除歐拉角和旋轉頻率外)的相對大小決定”這一性質。將涉及參數同時擴大或縮小對應倍數，展示不同倍數下的角多普勒曲線以證明該性質。不同倍數下的角多普勒曲線如圖9所示。圖11為微動參數(除歐拉角和旋轉頻率外)等比例縮小0.50,0.75和等比例放大1,2,4倍的曲線，5條曲線完全重合，證明了等比例縮小或放大微動參數并不影響角多普勒曲線。通過圖11可以證明所推導性質的正確性。

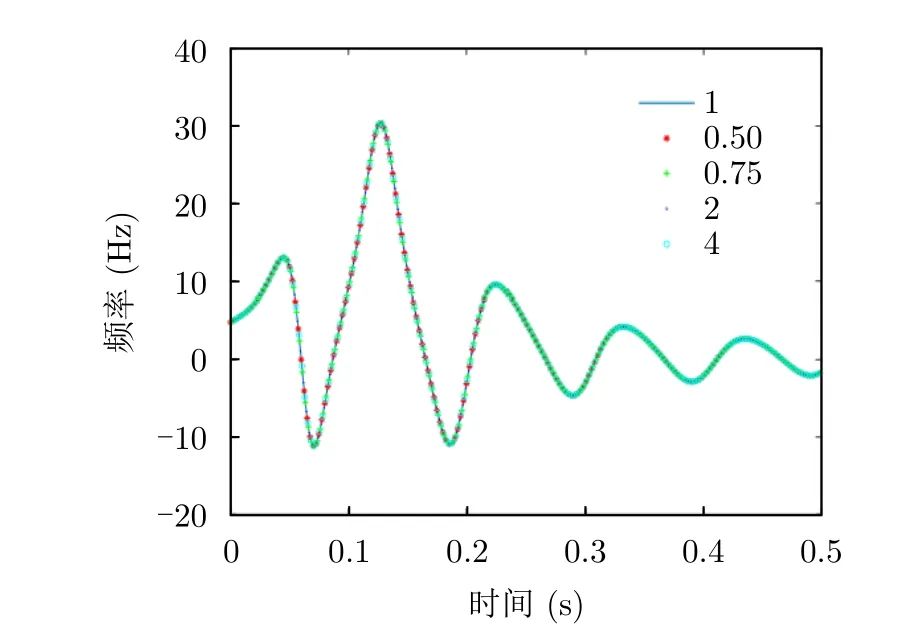
圖11 不同微動參數倍數下的角多普勒曲線Fig.11 Angular Doppler curves under different micro motion parameter multiples

在驗證所推導公式和性質的正確性后，根據圖7所示的算法提取旋轉目標微動參數。首先展示在利用完整周期的頻移曲線條件下的微動參數提取結果。線多普勒曲線的2階導數曲線和3階導數曲線如圖12所示，相鄰階導數曲線間峰值比例即為旋轉角頻率，由圖12所示曲線可估計旋轉角頻率為62.485 rad。同時，由線多普勒2階導數曲線幅度可估計徑向半徑為0.3736 m。

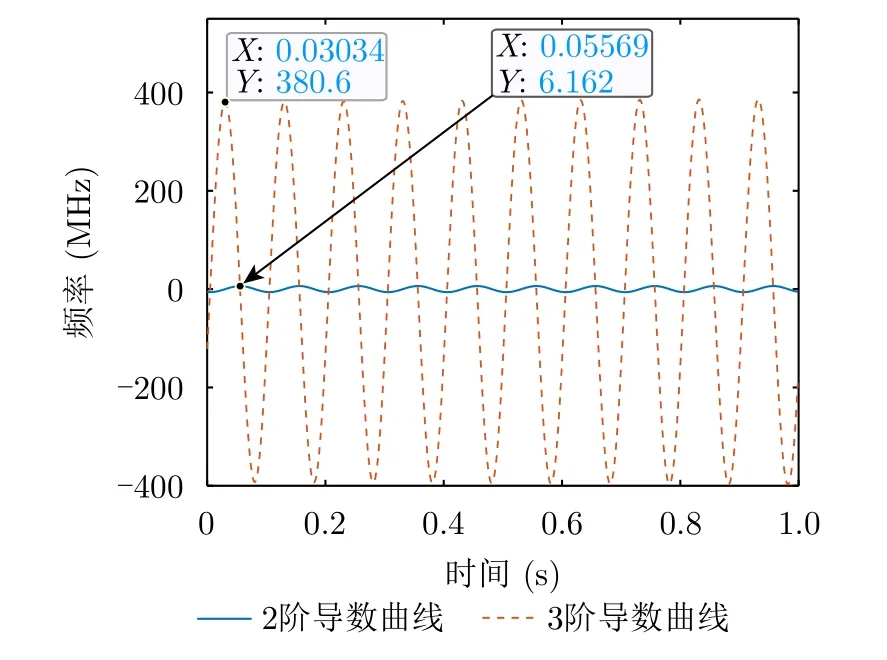
圖12 不同階導數下的線多普勒曲線Fig.12 Linear Doppler curve under different order derivatives

在估計旋轉角頻率和徑向半徑的基礎上，等間隔選取完整周期角多普勒頻移曲線上的8個點，這些點對應的時刻和角多普勒值如表2所示。

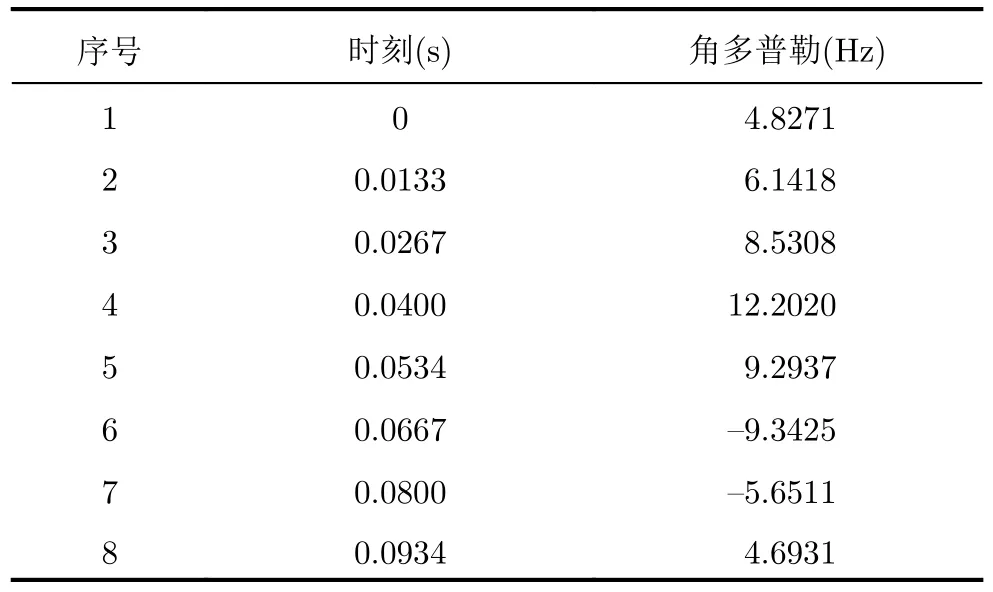
表2 選取點的時刻和角多普勒值Tab.2 The time and angular Doppler value of the selected point

將表2所示的數據代入方程(25)所示的多元非線性方程組中，即可求解歐拉角和剩余微動參數的相對大小。利用L-M算法求解多元非線性方程組，求解過程中的迭代誤差如表3所示。在迭代過程中算法的學習率在根據迭代誤差不斷變化，自適應的調節學習率提高了算法求解速度和準確率。隨著迭代次數的增加，誤差逐漸減小，最終誤差為5.26×10-15，代表算法成功求解方程組。多元非線性方程組的求解結果如表4所示，估計的歐拉角為(1.047,0.785) rad，與理想值基本一致，根據歐拉角可計算出旋轉矢量估計值 (0.707,-0.612,0.353)T。與提出角多普勒性質一致，根據角多普勒可精確估計目標歐拉角，但僅能獲得旋轉半徑、旋轉中心和速度矢量的相對大小。

表4 多元非線性方程組求解結果Tab.4 Solution results of multivariate nonlinear equations

在獲得目標歐拉角和徑向半徑的基礎上，根據式(12)，可獲得目標旋轉半徑估計值0.3982 m。與理想值0.4 m相比，旋轉半徑的估計值與理想值基本一致。將旋轉半徑估計值代入表4的估計結果中，算法最終獲得的微動參數估計結果如表5所示，提取誤差均小于1%，算法在利用完整頻移曲線的情況下實現了對平動旋轉目標微動參數的精確提取。

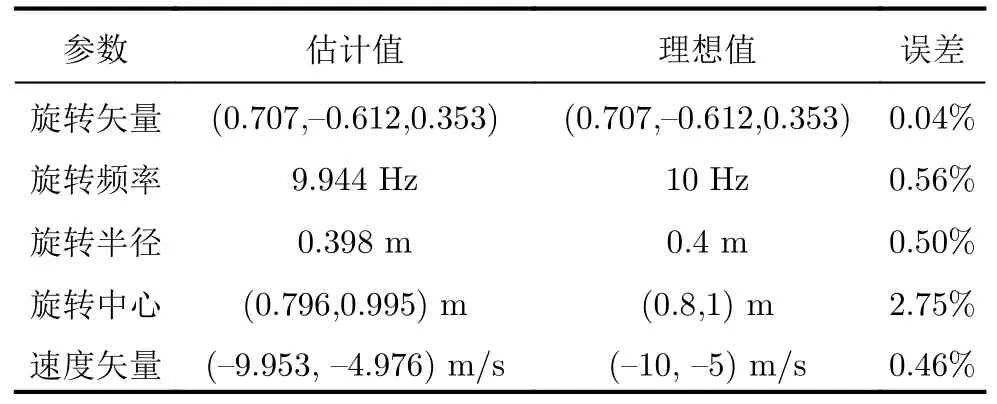
表5 完整周期頻移曲線下的微動參數估計結果Tab.5 Estimation results of micro-motion parameters under complete periodic frequency shift curve

前面討論了算法在利用完整周期頻移曲線時的性能，接下來討論頻移曲線長度對算法提取性能的影響，并給出在所示雷達和目標參數條件下算法提取目標微動參數所需的最短頻移曲線長度。此時線多普勒頻移曲線和角多普勒頻移曲線如圖13所示，圖13(a)為1/4微動周期的線多普勒頻移曲線，圖13(b)為1/4周期的角多普勒頻移曲線。

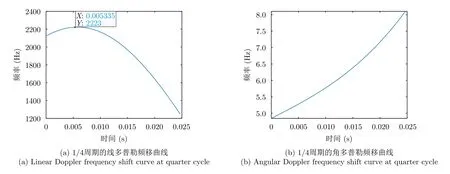
圖13 1/4周期的多普勒頻移曲線Fig.13 Doppler frequency shift curve at quarter cycle

從1/4微動周期線多普勒頻移曲線中提取目標微動參數的過程與完整周期頻移曲線中的提取過程一致。基于1/4微動周期線多普勒頻移曲線，可估計目標旋轉角頻率為62.485 rad，徑向半徑為0.3736 m。在估計旋轉角頻率和徑向半徑的基礎上，等間隔選取1/4微動周期角多普勒頻移曲線上的8個點，這些點對應的時刻和角多普勒值如表6所示。

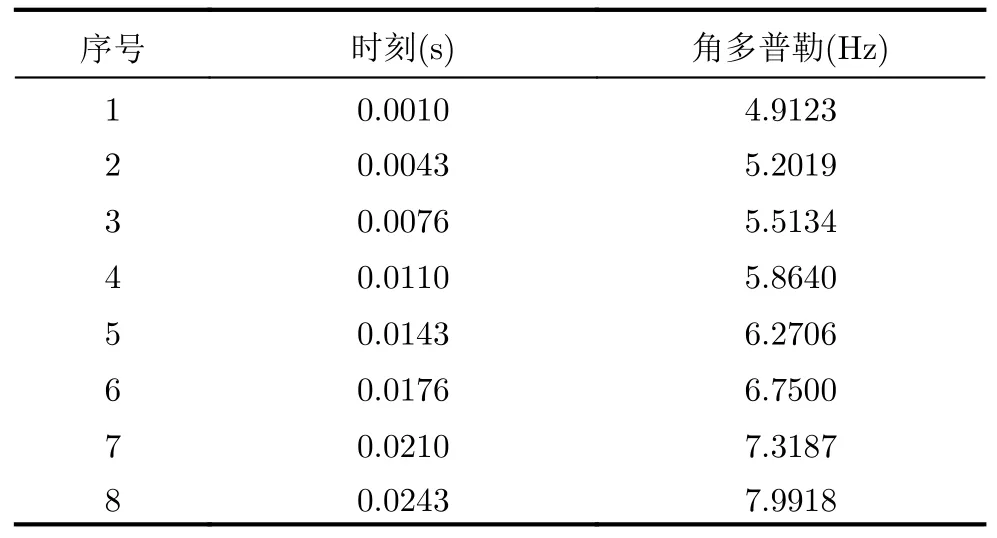
表6 選取1/4周期內8個點的時刻和角多普勒值Tab.6 Select the time and angular Doppler Values of 8 points within a quarter cycle

將表6所示的數據代入式(25)所示的多元非線性方程組中，利用L-M算法求解多元非線性方程組。由于只選取了1/4微動周期內8個點作為求解方程組的輸入，該情況下算法迭代了10909步才求得方程組的解，最后一步的誤差為2.0543×10-22，學習率為10-11。與利用完整周期頻移曲線相比，利用1/4周期頻移曲線所需求解時間為前者的840倍，計算時間明顯增加。基于角多普勒的方程組求解結果如表7所示，估計的歐拉角為(1.047,0.785) rad，與理想值基本一致。根據歐拉角可算出目標旋轉矢量估計值 (0.707,-0.612,0.353)T。在獲得目標歐拉角和徑向半徑的基礎上，根據式(12)，可獲得目標旋轉半徑估計值0.3982 m。與理想值0.4 m相比，旋轉半徑的估計值與理想值基本一致。將旋轉半徑估計值代入表7的估計結果中，算法最終獲得的微動參數估計結果如表8所示，提取誤差均小于1%，且與利用完整周期頻移曲線的提取誤差基本一致。仿真證明了算法在利用1/4微動周期多普勒頻移曲線的情況下可實現對平動旋轉目標微動參數的精確提取。

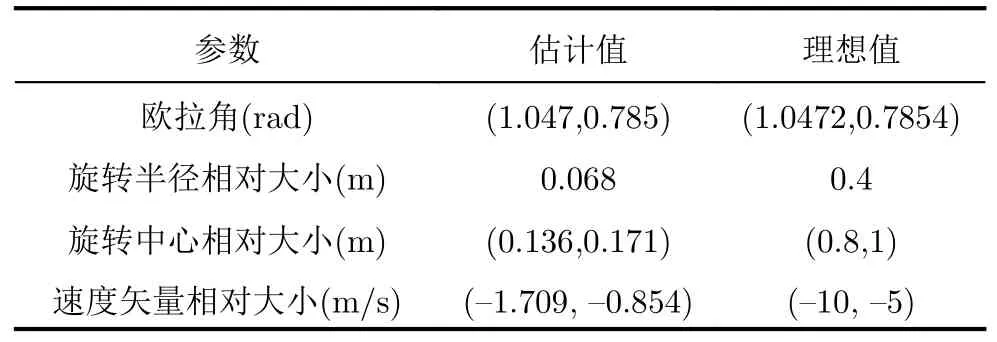
表7 1/4周期多元非線性方程組求解結果Tab.7 Solution results of multivariate nonlinear equations under 1/4 period

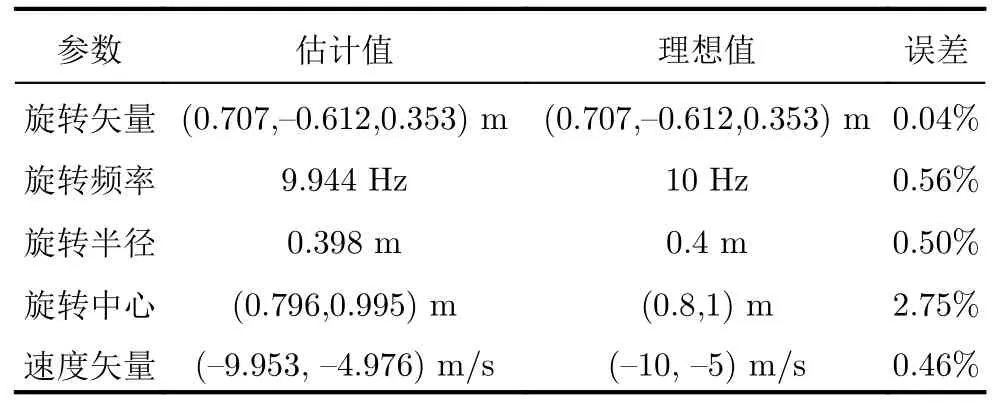
表8 1/4周期頻移曲線下的微動參數估計結果Tab.8 Estimation results of micro-motion parameters at quarter periodic frequency shift curve

實際應用中通常從時頻圖中提取目標角多普勒頻移曲線，噪聲干擾主要體現在角多普勒頻移曲線提取誤差中。為模擬噪聲干擾對提取誤差的影響，添加存在角多普勒提取誤差的情況下，目標微動參數的提取結果。在對角多普勒曲線添加范圍為[-10%,10%]的隨機誤差后，角多普勒曲線如圖14所示。

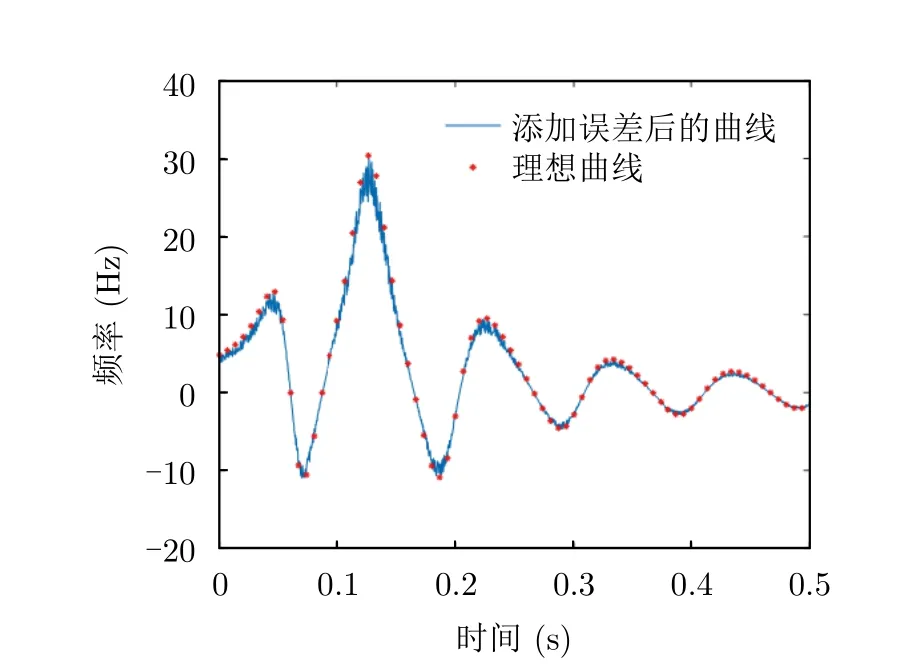
圖14 添加誤差后的角多普勒曲線Fig.14 Angular Doppler curve after adding error

添加隨機誤差后，曲線出現了明顯的波動，同一選取角多普勒曲線上的6個點，其結果如表9所示。由于添加了隨機誤差，6個點的誤差范圍在1%～20%，會對最終的微動參數提取結果造成一定的影響，其微動參數提取結果如表10所示。由于提取誤差的影響，微動參數提取誤差增大，其中速度矢量的誤差最大，達到15.18%；除旋轉頻率外，旋轉半徑的估計誤差最小，僅為2.62%。仿真證明了在角多普勒頻移曲線存在誤差時算法的適用性。

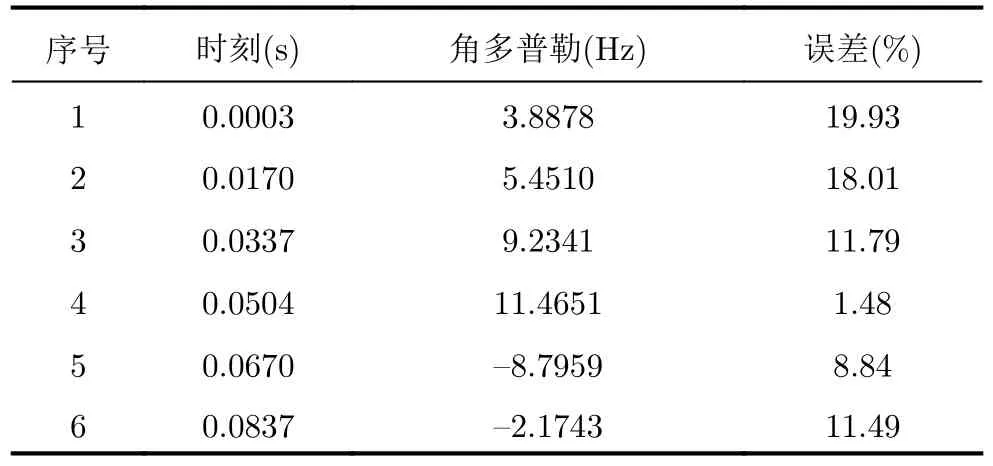
表9 添加誤差后6個點的時刻和角多普勒值Tab.9 Time and angle Doppler values of 6 points after adding error

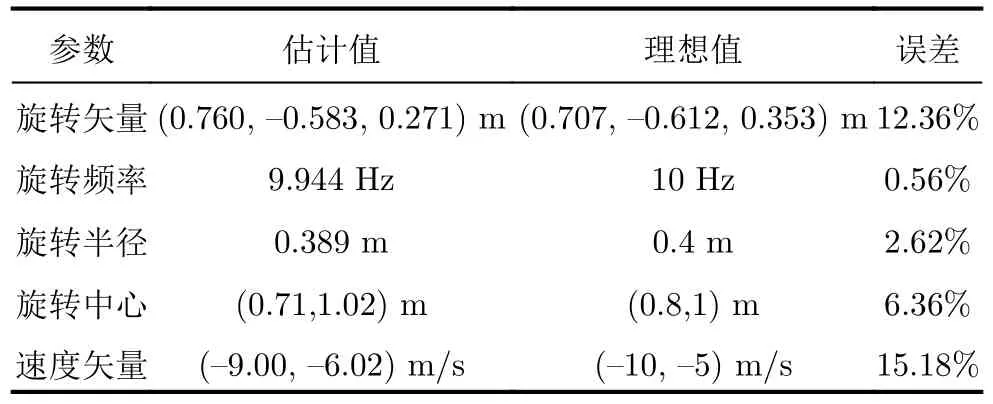
表10 添加誤差后的微動參數估計結果Tab.10 Estimation results of micro-motion parameters after adding errors

5 結語

渦旋電磁波雷達能觀測目標投影到雷達徑向和垂直于徑向平面的微動分量，可實現對目標三維微動參數的提取。本文主要研究了渦旋電磁波雷達平動旋轉目標微多普勒效應，提出了基于1/4微動周期多普勒頻移曲線的微動參數提取方法，獲得了目標旋轉頻率、旋轉半徑、旋轉矢量、平動速度矢量等參數。文章在獲得目標線多普勒頻移曲線和角多普勒頻移曲線的理想條件下，對目標微多普勒效應進行探討并提取目標微動參數，并未考慮各類因素對多普勒提取的影響。在實際應用中，由于時頻分析方法的時頻分辨率限制，對微動參數提取精度會帶來一定的影響；且線多普勒分量和角多普勒分量的分離精度也會影響微動參數提取精度，這些問題值得在下一步工作中繼續予以深入研究。我們將在下一步的工作中將電磁仿真和暗室實測相結合，驗證提出算法的正確性并根據測試結果不斷改進算法。