一種基于元學習的稀疏孔徑ISAR成像算法

夏靖遠 楊志雄 周治興 廖淮璋 張雙輝 付耀文

(國防科學技術大學 長沙 410073)

1 引言

逆合成孔徑雷達(Inverse Synthetic Aperture Radar,ISAR)可以全天時、全天候獲得遠程高機動目標的高分辨率圖像，已經逐漸成為獲取目標觀測數據的主要工具[1]。高分辨率ISAR圖像對于雷達目標識別、分類和語義分割等后續任務至關重要。雖然從完整的雷達回波獲取清晰的雷達圖像并不困難，但是雷達系統往往受到雷達硬件和客觀成像條件的限制，難以獲得完整的雷達回波。稀疏孔徑ISAR成像就是通過稀疏建模從不完整的回波中恢復和重建ISAR圖像，在雷達目標識別、空間監視、彈道導彈防御等軍用民用領域具有重要意義[2]。

現有的稀疏孔徑ISAR成像算法主要分為基于模型的方法和基于深度學習的方法兩大類。早年的稀疏孔徑ISAR成像算法以基于模型的方法[3-12]為主，其通常根據目標ISAR圖像特性(例如稀疏性)，手動設計ISAR圖像先驗模型。具體來說，匹配追蹤(Matching Pursuit,MP)[3]是經典基于模型的稀疏孔徑ISAR成像方法，其利用ISAR圖像具有稀疏性，通過多次迭代運算求得ISAR圖像最稀疏解。正交匹配追蹤算法(Orthogonal Matching Pursuit,OMP)[4]在MP算法的基礎上，在分解的每一步中對所選元素進行正交化處理，在成像精度相同的情況下提升了收斂速度。交替方向乘子法(Alternating Direction Method of Multipliers,ADMM)[5]在現有的凸優化求解框架下，利用范數正則項對待恢復信號的稀疏性進行約束，并在此基礎上最小化待恢復信號與原始信號的誤差。總的來說，基于模型的方法的優勢在于數學模型成熟，算法的收斂性和數學可解釋性較好。然而，基于模型的方法包含需要手工調整的超參數，對成像效果影響較大，且容易收斂到局部最優，不能有效地滿足ISAR圖像成像任務在復雜多變條件下的成像需求。

隨著近年來深度學習的快速發展，基于深度學習的方法[13-23]通常設計一個端到端的深度神經網絡模型，例如，深度卷積神經網絡[13]、生成對抗網絡[14]等。通過大量配對數據訓練后，能夠實現對各種圖像恢復、重構任務的有效求解，但應用領域主要在于光學圖像修復、超分辨、降噪等，在稀疏孔徑ISAR成像方面應用較少。文獻[15,16]提出了一種基于深度卷積神經網絡的ISAR成像方法，通過引入深度卷積神經網絡來代替基于模型方法正則化迭代求解步驟，從而實現了較好的成像性能。文獻[17,18]提出了一種基于生成對抗網絡ISAR成像算法，通過引入對抗損失，使得ISAR成像結果具有更好的細節紋理信息。上述方法的優點在于具有較好的數據驅動性能，但是這類方法受限于訓練數據的同時，也不具備數學可解釋性，不能適應條件多變的ISAR成像任務需求。文獻[19]提出了基于深度展開的ADMM算法，通過深度學習的方法實現ADMM算法迭代求解中的部分步驟和超參數，使得方法具有數據驅動性能的同時，也具備較好的數學可解釋性。然而這類方法仍然依賴大量的配對訓練數據和預訓練過程，而高質量的ISAR圖像公開數據集較少且通常難以獲得，訓練數據集的質量對算法效果有較大影響。

在最近的非凸優化算法理論研究中，文獻[24,25]提出了一種基于元學習的交替迭代最小化框架，在不需要任何訓練數據和預訓練過程的情況下，在傳統的變量優化問題上取得了較好的收斂性能。這一優點非常契合稀疏孔徑ISAR成像任務。受文獻[24,25]啟發，本文提出了一種基于元學習的高效、自適應稀疏孔徑ISAR成像算法。所提方法通過學習輔助的交替迭代優化方式，一方面將ISAR成像問題中對ISAR圖像的迭代求解轉化為了對網絡輸入和網絡參數的交替迭代更新求解，從而避免了算法對訓練數據的依賴和算法的預訓練需求。針對算法在求解過程中陷入局部最優這一核心問題，所提方法引入基于元學習的優化求解策略，通過考慮多次迭代步驟的累積誤差來對優化策略進行實時更新，實現在全局視野中考慮到更全面的優化軌跡，從而達到算法自適應地根據收斂軌跡學習優化更新的方向和步長，從本質上確保了避開局部最優的能力。最后，基于仿真的目標ISAR圖像數據設計了多組對比實驗，實驗結果表明：本文方法可以在沒有訓練數據、沒有預訓練的情況下進行高效自適應的稀疏孔徑ISAR成像，并獲得優于其他常規ISAR成像算法的性能。

2 稀疏孔徑ISAR成像問題概述

本節首先介紹了稀疏孔徑ISAR成像模型，然后以交替方向乘子法為例，介紹了稀疏孔徑ISAR成像問題求解過程。

2.1 ISAR成像模型

一個常見的ISAR成像場景如圖1所示。在目標中心建立了一個坐標系，其中，y軸沿著雷達的視線(Line-Of-Sight,LOS)方向，x軸垂直于y軸。假定雷達與被探測目標位于同一平面，則該平面構成成像平面。在實際應用中，由于雷達相干處理間隔(Coherent Processing Interval,CPI)很短，因此目標在相干處理間隔內可等效為勻速運動，目標旋轉速度設為ω。所獲取目標的一維高分辨距離像(High Resolution Range Profile,HRRP)，表示如下：

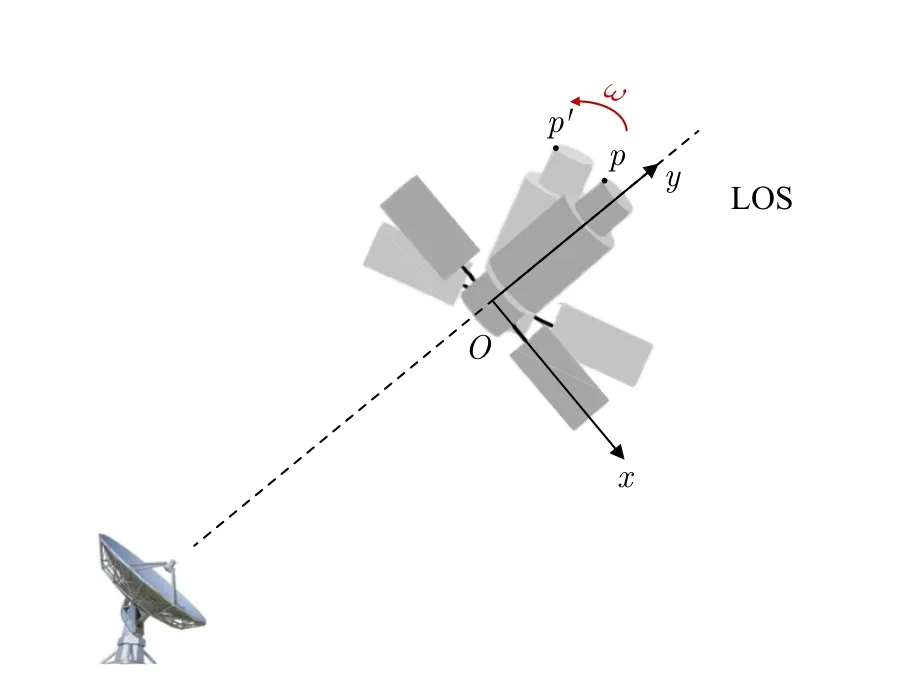
圖1 ISAR雷達觀測模型Fig.1 General ISAR imaging scenario

其中，τ表示快時間，t表示慢時間，fc表示中心頻率，c表示光速，B表示信號帶寬，σp表示散射點p的反射系數，P表示總散射點個數，rp(t)表示雷達到目標第p個散射中心的距離，rp(t)可以進一步分為平動分量rp,t(t)和 轉動分量rp,r(t)兩個部分：

其中，xp和yp為目標第p個散射點在圖1中參考坐標系下的坐標。由于雷達CPI很短，式(2)中轉動分量rp,r(t)的高階分量可以忽略。在信號模型中，我們假設回波信號已經完成包絡對齊和自聚焦等補償操作，最終回波表達式如下所示：

此時的回波信號可通過方位向快速傅里葉變換得到目標的散射點分布。對于式(3)，考慮到信號中的加性回波噪聲，式(3)可寫為

通過對快時間維進行快速傅里葉變換，式(4)中的回波表達式s(τ,t)可以得到ISAR一維距離像信號矩陣S，通過對慢時間維進行傅里葉變換，ISAR一維距離像信號矩陣S可以得到ISAR圖像X。上述過程可進一步寫成離散矩陣的形式，如下所示：

其中，S ∈CL×N表示回波一維距離像，X ∈CM×N表示二維ISAR像矩陣，A∈CL×M表示ISAR圖像的退化矩陣，N ∈CL×N表示二維ISAR像的高斯白噪聲矩陣。L表示稀疏回波下的方位向脈沖數，M表示原始回波下的方位向脈沖數，N表示距離像單元數。

在稀疏孔徑ISAR成像場景中，觀測矩陣A可建模為降采樣矩陣D ∈CL×M與傅里葉變換矩陣F ∈CM×M相乘的形式A=DF。一般情況下，傅里葉變換矩陣F與降采樣矩陣D是已知且確定的。降采樣矩陣D的形式與稀疏模式以及稀疏率有關，其中隨機稀疏模式是目前常見的一種稀疏采樣模式，表示對完整的回波信號進行隨機的采樣、抽取。稀疏率表示降采樣矩陣D中值為1的行數與總行數的比例。

在稀疏孔徑ISAR成像問題中，式(5)可以被進一步改寫成以下矩陣形式：

對于ISAR圖像X的恢復，需要引入先驗信息來構造解的約束條件，理想情況下，信號的稀疏性由l0范數約束，它表示信號的非零元素數量。但在l0范數約束下，優化問題是一個NP難問題，通常使用其他約束松弛這一問題。在壓縮感知中，l1范數的優化問題是凸優化問題，為了計算方便，因此常見的做法是將l0范數用l1范數代替，此時該優化問題可以寫成如下形式：

其中，β表示正則化參數。

2.2 ADMM方法

為了求解上述優化問題，通常利用ADMM方法對問題進行交替迭代求解。該算法首先引入隱變量H，將無約束優化問題式(7)轉化為以下約束優化問題的形式：

根據式(8)可進一步寫出其增廣拉格朗日函數：

其中，ρ表示懲罰系數，α∈CM×N表示拉格朗日乘子，αH表示矩陣α的共軛轉置。ADMM算法將問題拆解成兩個子問題，并通過交替迭代最小化的方式對其進行分別優化，最終可以得到如下迭代過程：

其中，上標 (k)表示迭代次數。對于式(10)中前兩個迭代過程，令Lρ(X,H,α)對X與H的偏導數分別為0可得到相應變量值的閉式解，式(10)中第3個迭代可直接計算得到，α與ρ為超參數，實際應用時通常根據問題和應用場景進行設定。

3 所提基于元學習的稀疏孔徑ISAR成像算法

本文方法主要由基于學習輔助的交替迭代求解和元學習優化兩部分組成，本節首先介紹基于學習輔助的交替迭代優化模塊。然后在此模塊的基礎上，介紹所引入元學習優化策略。最后介紹本文算法的總體實現流程以及計算復雜度分析。

3.1 基于學習輔助的交替迭代優化

稀疏孔徑ISAR成像問題的矩陣形式如下所示：

其中，第1項為數據保真項，第2項為先驗項。令k為迭代次數，在第k次迭代中，本文方法并不像傳統算法一樣直接求解ISAR像X(k)，而是通過引入一個復數神經網絡GX作為ISAR像生成網絡輔助求解式(11)。其中，ISAR像X(k)由一個復數神經網絡GX生成，網絡GX的輸入為一個高斯噪聲ZX ∈CM×N，噪聲ZX ∈CM×N隨算法的更新迭代過程而更新，ISAR像X(k)的生成過程如下所示：

對于式(13)這種多變量優化求解問題，通常采用交替迭代最小化算法進行求解，表示如下：

3.2 元學習優化

由于式(11)的病態性，直接通過式(16)和式(18)窮盡地對網絡輸入ZX和 網絡參數θX進行交替迭代求解仍然容易陷入局部最優解。本文提出一種基于元學習交替迭代求解策略，利用一段累積的損失LθX作為元學習損失Lmeta并用于更新網絡參數θX，元學習損失的計算表示如下：

其中，k表示網絡元學習更新的迭代次數，T表示一次元學習損失計算利用的損失LθX數量。通過Adam優化器優化更新網絡參數θX，表示如下：

值得注意的是，傳統元學習往往需要少量訓練數據作為樣本來訓練網絡模型，網絡模型在多個不同任務下進行訓練，使得模型具備更好泛化性能。本文所提的元學習方法與傳統元學習方法不同的是：本文所提的元學習方法將算法的一次迭代過程視為元學習的訓練樣本，通過跨多個不同的迭代過程的元學習損失Lmeta對網絡參數進行更新，使得算法具有更好全局更新視野。在這種情況下，網絡參數不再最小化每個單獨的圖像重建損失LθX，而是通過最小化累積的元學習損失Lmeta來優化網絡參數，因此實現了一種非貪婪且自適應的優化策略。更多的元學習優化細節可以參考文獻[24,25]。

3.3 整體實現

本文方法的總體實現流程如算法1所示。其中，網絡GX的結構示意圖如圖2所示，網絡GX為一個8層的全卷積神經網絡，從輸入到輸出的卷積通道數分別為1,16,32,64,128,64,32,16,1，卷積核大小均設置為N=3×3，圖2中綠色箭頭、紅色箭頭、藍色箭頭和黑色箭頭分別表示卷積層、池化層、轉置卷積層和跳躍連接。網絡GX的所有網絡參數在隨機初始化后，通過本文所提的元學習策略進行優化。值得注意的是，利用式(15)和式(17)計算得到的損失更新網絡輸入與網絡參數時，網絡輸入ZX和網絡參數θX是沒有經過任何預訓練的，也不需要任何的訓練數據。在實際應用中，網絡輸入ZX和 網絡參數θX從一個完全隨機初始化的開始，將每一次迭代過程視為一個訓練樣本，隨著問題式(14)的迭代求解而更新，即實現了一種“即插即用”的在線求解模式。

算法 1 一種基于元學習的稀疏孔徑ISAR成像算法Alg.1 A meta-learning based sparse aperture ISAR imaging method

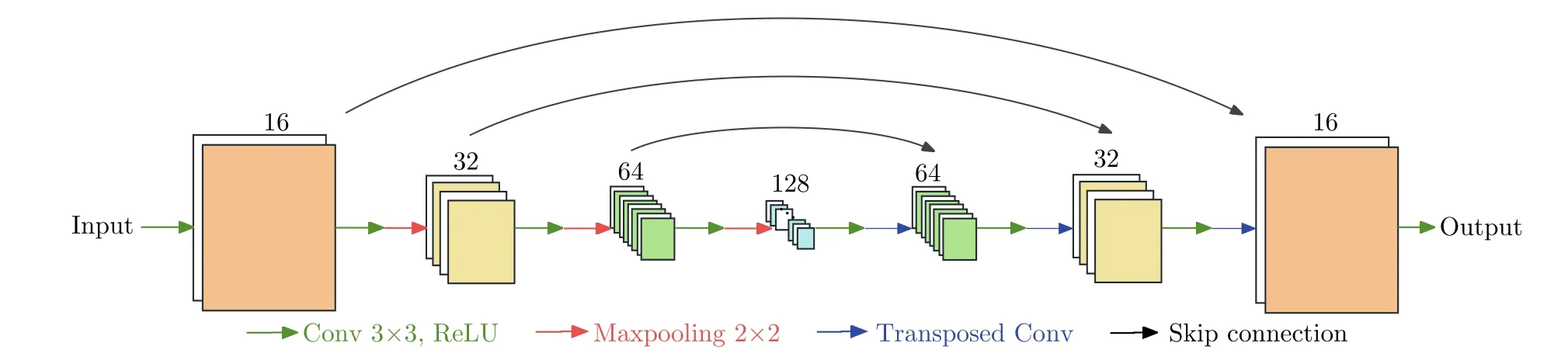
圖2 本文方法網絡結構示意圖Fig.2 The network architecture of the proposed method

綜上所述，本文所提出的基于元學習的稀疏孔徑ISAR成像算法在求解過程中，通過式(12)，將對變量求解的優化問題轉化成了對網絡輸入和網絡參數求解的優化問題。通過式(14)將原問題分解成了兩個子問題，并進行交替迭代求解，實現了一種“即插即用”的在線求解模式，避免了方法對訓練數據的依賴性。而元學習的優化迭代策略則通過式(19)和式(20)計算迭代過程中累積的元學習損失，并用于更新網絡參數，最終實現了一種自適應、非貪婪的優化策略，保證了算法的稀疏孔徑ISAR成像性能。

3.4 計算復雜度分析

4 實驗結果與分析

4.1 實驗設置

本文所用測試數據集是一個仿真的空間目標ISAR圖像數據集和一個實測數據集。其中仿真數據集共有3000張空間目標ISAR圖像，包含3個不同角度的3種不同空間目標。實測數據集包含類別為Yak42的飛機目標。其中每張空間目標ISAR圖像的大小為240×240。在測試階段，本文方法不使用任何數據進行訓練，也沒有任何的預訓練過程，在求解過程中僅僅已知ISAR一維距離像S。考慮到空間目標ISAR圖像通常是灰度圖像，圖像的可視化效果較差。為了達到增強ISAR圖像可視化效果的目的，我們通過偽彩色渲染增強灰度ISAR圖像，以獲得更好的可視化效果。在對比實驗中，本文方法將對比基于模型的ISAR成像方法：距離-多普勒(Range-Doppler,RD)算法、正交匹配追蹤(Orthogonal Matching Pursuit,OMP)算法[4]和ADMM算法[5]，以及基于學習的ISAR成像方法：基于復數展開網絡的ADMM (Complexed-Unfolding ADMM,CU-ADMM)算法[19]。ISAR圖像質量評價指標采用峰值信噪比(Peak Signal-to-Noise Ratio,PSNR)、均方根誤差(Root Mean Squared Error,RMSE)和圖像熵3個數據指標。

4.2 實驗結果及分析

表1給出了在稀疏率為0.25的情況下，5種不同ISAR成像方法在仿真數據上得到的圖像熵、PSNR值和RMSE值。在表中我們能夠發現本文方法在所有條件下都實現了最好的ISAR成像性能。尤其是在PSNR指標上，本文方法高出性能第2名算法0.79 dB。表2進一步給出了稀疏率在0.125條件下，不同方法的對比結果。我們可以看到本文方法仍然實現了最好的性能。圖3進一步展示了所有ISAR成像方法在兩種稀疏率條件下的可視化結果對比。我們可以看到本文方法的ISAR成像結果在定性的視覺效果上均更接近真值ISAR圖像。

表1 不同方法在仿真ISAR數據集上的平均成像性能對比(稀疏率為0.250)Tab.1 The average imaging results on the of the simulated ISAR data (sparsity rate 0.250)

表2 不同方法在仿真ISAR數據集上的平均成像性能對比(稀疏率為0.125)Tab.2 The average imaging results on the of the simulated ISAR data (sparsity rate 0.125)

圖3 不同ISAR成像方法在仿真數據上的可視化對比結果Fig.3 The visual imaging results on the of the simulated ISAR data

表3和表4分別給出了稀疏率為0.250和0.125的情況下，5種ISAR成像方法在實測數據上得到的圖像熵、PSNR值和RMSE值。在表中我們能夠發現本文方法在所有條件下都實現了最好的ISAR成像性能。尤其是在稀疏率更低的條件下(稀疏率為0.125)，本文所提方法在PSNR指標上高出性能第2名算法0.51 dB。圖4和圖5進一步展示了所有ISAR成像方法在實測數據上兩種稀疏率(0.250和0.125)條件下的可視化結果對比。可以看到本文方法的ISAR成像結果在定性的視覺效果上均更接近真值ISAR圖像。

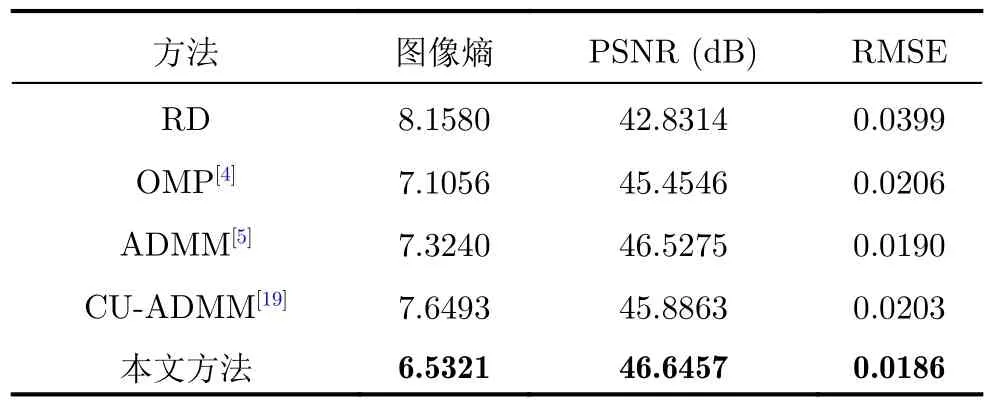
表3 不同方法在實測ISAR數據集上的平均成像性能對比(稀疏率為0.250)Tab.3 The average imaging results on the of the real ISAR data (sparsity rate 0.250)

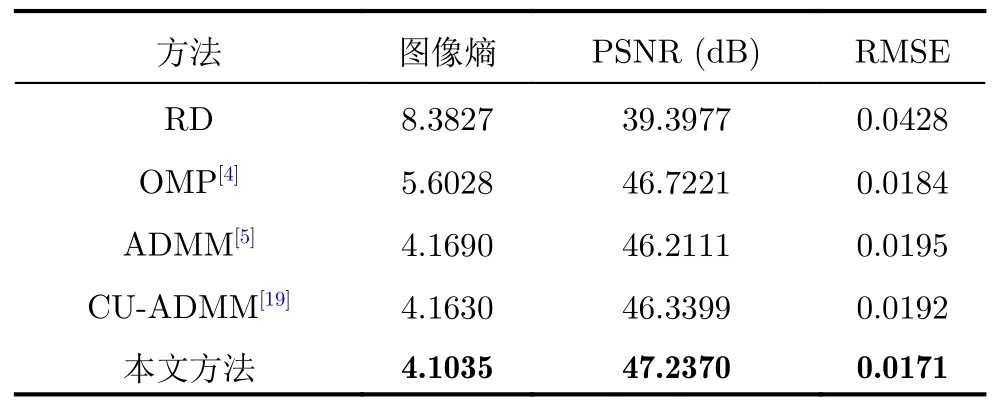
表4 不同方法在實測ISAR數據集上的平均成像性能對比(稀疏率為0.125)Tab.4 The average imaging results on the of the real ISAR data (sparsity rate 0.125)

圖4 不同ISAR成像方法在實測數據上的可視化對比結果(稀疏率為0.25)Fig.4 The visual imaging results on the of the real ISAR data (sparsity rate 0.25)

圖5 不同ISAR成像方法在實測數據上的可視化對比結果(稀疏率為0.125)Fig.5 The visual imaging results on the of the real ISAR data (sparsity rate 0.125)

4.3 消融實驗

表5和圖6分別給出了本文方法中所引入的元學習優化策略在仿真數據上的消融實驗結果。其中“無元學習模塊”表示本文方法不采用元學習的求解策略，當T設置為1時，也就是當元學習僅累積1次梯度信息時，本文所提的元學習方法退化為經典的交替迭代最小化方法。在表5中我們能夠發現本文方法在所有條件下都實現了最好的ISAR成像性能。本文方法在沒有引入元學習模塊的情況下，出現了1 dB左右的PSNR值性能下降，而圖像熵和RMSE評價指標也有一定程度的性能下降。因此，該消融實驗驗證了本文方法中元學習優化策略的有效性。

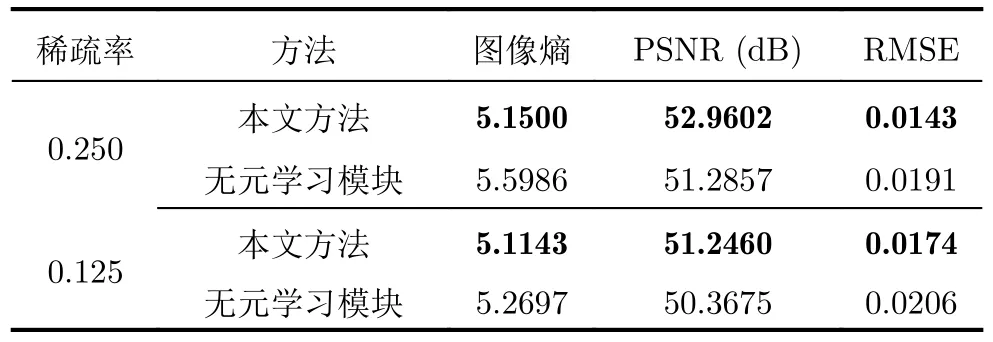
表5 本文方法中元學習優化的消融實驗Tab.5 The ablation studies of the proposed method

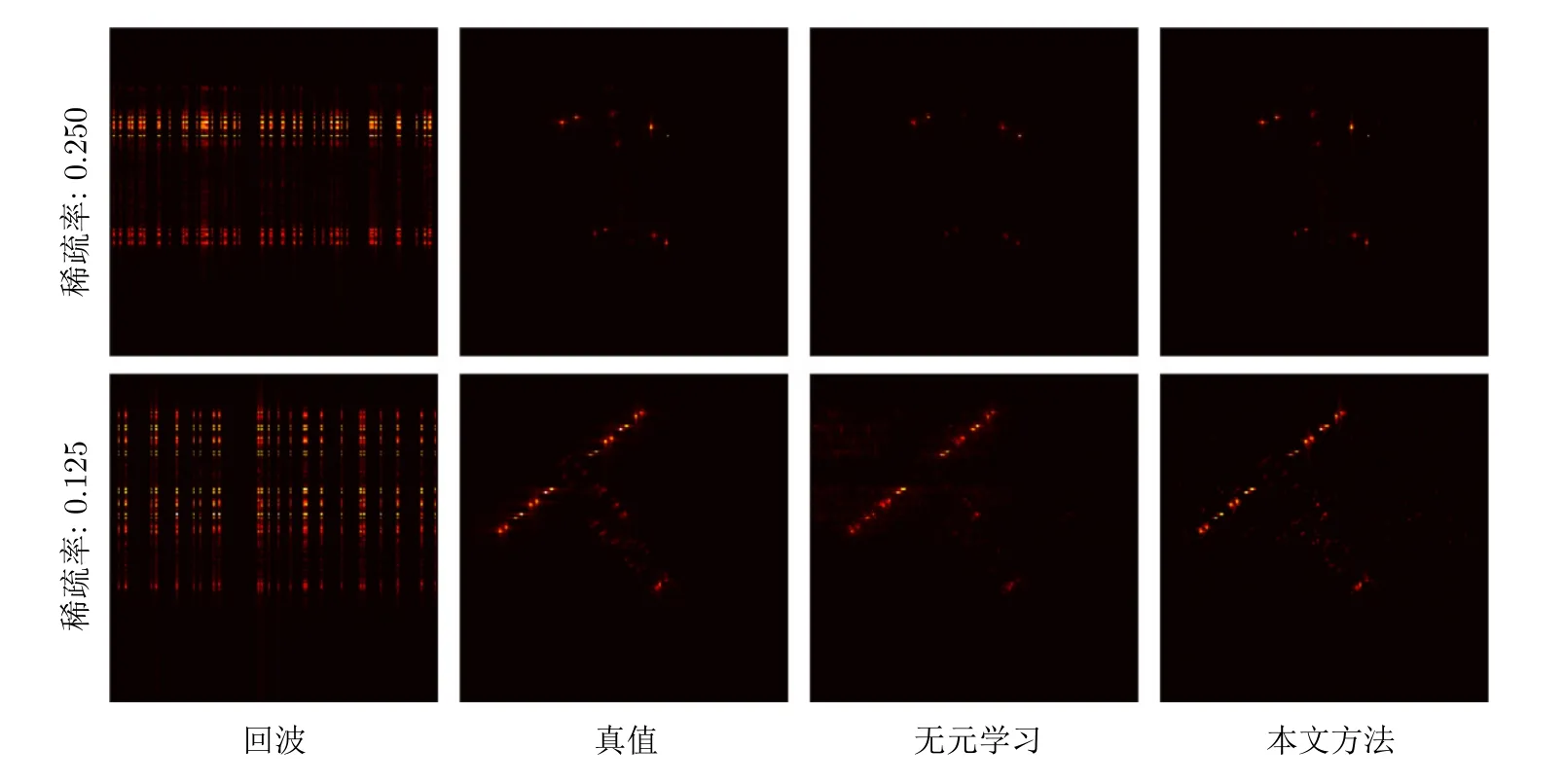
圖6 消融實驗成像結果Fig.6 The visual results of the ablation studies of the proposed method

4.4 計算復雜度

表6給出了5種不同ISAR成像方法的計算復雜度對比，其中計算機CPU為Intel Core i7-11800H，顯卡配置為GeForce RTX 3090 GPU。從表6中可以發現本文方法的測試時間較大。這是因為元學習優化迭代策略的引入，本文方法在測試的迭代過程中需要反復對網絡參數進行更新。但是本文方法的計算復雜度是較低的，僅與ISAR圖像大小M的2次方成正比，且沒有訓練時間消耗。綜合考慮算法的計算復雜度、訓練時間以及測試時間，本文方法具有適中的計算成本。

5 結語

本文提出了一種基于元學習的高效、自適應稀疏孔徑ISAR成像算法。所提方法通過學習輔助的交替迭代優化方式，避免了方法對訓練數據的依賴；本文方法通過基于元學習的優化求解策略，從本質上確保了避開局部最優的能力。最后，本文方法在含有多種不同的ISAR仿真、實測數據集上進行了廣泛的對比實驗并在圖像熵、PSNR值和RMSE值3個評價指標上均實現了更好的ISAR成像性能。但本文方法的運算效率還有進一步提高的空間，且并沒有考慮到的ISAR成像過程中的運動補償。后續我們將針對ISAR運動補償與稀疏孔徑成像一體化問題開展研究。