雷達目標識別評估中的數據可分性度量方法

姜衛東 薛玲艷 張新禹

(國防科技大學電子科學學院 長沙 410073)

1 引言

測試和評估是目標識別模型中重要的組成部分，是衡量模型性能的重要手段[1]，識別評估方法相對識別模型的研究滯后[2]，這在一定程度上限制了目標識別模型實用化發展。目前在評估階段，研究學者更傾向于在特定數據集上給出識別準確性指標來評價所提模型的性能優勢[3]。該方法僅從識別率一個方面評價了模型性能，無法反映在輸入數據發生變化時識別模型的泛化能力[4,5]。其原因是面向模型的準確性評估指標無差別地對待了每一個數據集，忽略了數據集可分性對識別性能造成的影響[6]。識別性能與數據可分性密切相關，識別性能的評估應當結合對數據特性的評估，以滿足對模型泛化性能的評估需求。考慮到真實雷達目標識別場景的多樣復雜與動態變化特性，要求實用化的目標識別模型應當具備一定的泛化能力。因此針對某個特定的識別任務，如基于雷達散射截面積 (Radar Cross Section,RCS)、基于高分辨距離像 (High-Resolution Range Profile,HRRP)或基于逆合成孔徑雷達 (Inverse Synthetic Aperture Radar,ISAR)像的目標識別任務，需要在不同觀測條件的數據上測試模型以評估其應對復雜目標識別環境的泛化性能。而評估模型泛化性能離不開對識別場景的描述，因此提出數據可分性度量量化模型所處識別條件。

數據可分性是在給定標簽條件下，描述數據中屬于不同類別的樣本間混合程度的一種固有屬性[7]。在已知數據標簽條件下，可以以具體的識別任務為導向，確定樣本依其類別在特征空間的分布，數據整體分布的擴展率與類別子空間類內分布的壓縮率共同構成數據可分性的衡量指標。可分性較好的數據具有較大的整體分布散度與較小的類內分布散度，表明類間樣本相關性弱而類內樣本相關性強。精確描述數據可分性有利于探究模型識別性能邊界，能夠預先為識別結果提供參考基準，為模型性能評估與改進提供支撐。

數據可分性度量為建立具有一定難度梯度的標準測試數據庫提供依據，為實現層次化、輕量級的模型泛化性能評估過程打下基礎。雷達目標識別數據集的可分特性受到目標所處環境、傳感器狀態等因素的影響，待識別的任務是在不同信噪比、不同信雜比、不同分辨率、不同觀測角或不同頻段下的目標散射特性信息集合。若將模型同時測試在上述所有狀態的數據集上，不僅耗費時間成本，并且無法得出指導性的評估結論，因此考慮一種更為輕量高效的層級式模型性能測試方法。如圖1，層級式模型識別性能評估中，模型由易到難每次測試在一個難度級別的數據集上，通過設置一定的識別率門限作為模型通過某層數據集測試的條件，模型在最終未通過測試的數據層所表現出的識別率代表了模型的性能上限，而模型通過測試的各數據層則體現模型性能的泛化范圍。上述測試方法的實施建立在對大規模數據按照其識別的難易程度進行分層的整理和歸納的基礎上，量化的數據可分性數值標定了數據的識別難度，為數據分層提供科學的依據。

圖1 層級式模型識別性能評估示意圖Fig.1 Hierarchical model recognition performance evaluation schematic

數據復雜度標定了識別任務難度[8]，決定了模型識別性能上限[9,10]。文獻[11]將數據空間的結構與特性分析列為人工智能的重大數理基礎問題之一。文獻[12]研究表明可分性因素的分析有利于輔助預測識別模型的性能。文獻[13]認為可分性度量可以應用于識別模型選擇、特征挑選算法、聚類算法、生成對抗網絡性能的評估，以評估挑選的特征、新聚類的數據及新生成樣本的可分性。文獻[14]依據分類復雜度設計了動態多分類器決策方法。文獻[15]將可分性度量結合到自編碼器網絡損失函數的迭代過程中，實現了對數據更可分低維特征的提取，將提取的隱藏層特征應用在下游識別任務中，提升了識別性能，并在評估階段將特征可分性作為網絡性能評估的指標之一。因此將數據可分性度量結合進雷達目標識別評估過程，對解釋、指導模型性能改進具有重要實際應用意義。

現有數據可分性度量方法大都基于對數據簡單統計特性或對樣本間距離的分析。文獻[16]從數據可分性角度總結了現有分類復雜度的度量方法，該文獻將數據復雜性度量歸為6類。其中，基于統計特征的分析方法僅利用了數據的均值和方差特性；線性度量方法主要依賴于線性分類器的識別結果；近鄰度量方法更側重于分析數據的局部距離信息；網圖度量方法主要衡量樣本點依據一定準則所構成的圖結構密度；樣本數與維度數指標主要用于描述類不平衡性及降維復雜度。上述方法僅反映了數據的局部特性，其有效性大多基于數據的線性可分假設，無法區分具備非線性劃分結構的特征族可分性差異[17]。文獻[13]驗證了基于統計特征、線性分類器、樣本數與維度數的度量方法無法有效衡量數據可分性；而基于鄰域和網圖的距離度量方法則具有較大的計算量，并且在衡量類間重疊度的實驗中不再適用。

為解決上述度量失效問題，本文考慮從概率論的角度解釋數據可分性。根據貝葉斯準則，假設每個類別出現的概率相等，則樣本分類的結果取決于每個類別相對應的似然函數大小[18]。此時各類別的似然函數差距越大，數據就越容易劃分開。然而由于高維數據的復雜性，似然函數建模比較困難。文獻[19]表明最小化數據編碼率的過程等價于求解似然函數的最優解，即數據編碼速率和參數估計性能具有強一致性[20]。這意味著如果按類別編碼后的數據可以用更好的概率分布模型擬合，則該數據在給定失真率下具有較小的編碼量。文獻[21]認為，率失真函數為實值混合數據的分割優度提供了一種自然的衡量標準。在最近的研究中，率失真理論被用于解釋神經網絡模型[22]、優化特征學習方法[23,24]等。

本文的主要貢獻在于基于率失真理論量化數據整體分布散度與類內分布散度，通過構造兩種分布散度的比例關系提出了一個新的數據可分性度量，該度量綜合了數據經奇異值分解后各個正交特征維度上的可分性信息，能夠評估多維高斯分布數據的可分性優劣；結合高斯混合模型，該度量能夠衡量非高斯分布數據的類間重疊度，度量效果相對現有方法具有明顯優勢。在仿真數據上對所提方法進行了測試，結果表明由所提方法計算的可分性度量值在二維數據上與特征散點圖可分性的直觀判定結果對應，并且能夠衡量加噪數據的可分性優劣；在高維實測數據[25]上的識別難度評估實驗表明所提度量與模型統計得到的平均識別率具有強相關性，其能夠以獨立于識別過程的方式量化數據識別難度，預先為識別結果提供評判基準；最后本文將所提度量應用在識別網絡特征質量評估中，在測試階段量化分析了網絡提取特征的可分性變化趨勢，在訓練階段將特征可分性作為損失函數的一部分來同時優化特征質量，從特征可分性的角度為網絡識別性能的評估與提升提供新思路。

2 相關工作

本節總結本文所用到的對比方法，其特點是利用樣本間的距離信息構造可分性度量。文獻[26]總結了一系列近鄰方法，如描述類內距與類間距相對比值的方法(Ratio of Intra/Extra Class Nearest Neighbor Distance,N2)以及一種統計局部近鄰數量的方法[27](Local Set Average Cardinality,LSC)；基于網圖的方法如網圖平均密度法(Average Density of the Network,Density)[28]主要描述依據一定距離判決準則所構造的網圖鄰接邊數量；此外文獻[13]提出基于距離的可分性度量指標(Distance-based Separability Index,DSI)，其主要利用類內距與類間距分布之間的差異信息。下面介紹上述度量方法的計算原理及特性。

(1) N2

N2度量方法設數據X=[x1,x2,...,xm]∈Rn×m由具有n維特征的m個樣本構成，計算樣本xi到其最近鄰同類樣本 NN(xi)距離d(xi,NN(xi))及xi到其最近鄰異類樣本 NE(xi) 的距離d(xi,NE(xi))，取m個樣本的d(xi,NN(xi)) 之 和與d(xi,NE(xi))之 和的比值即為度量N 2。由于N 2 的數值范圍取N2∈[0,∞)，因此通過數值轉換將其規范到0～1之間，且值越大，表明數據越不可分，如式(1)

式(1)表明度量N2利用的是樣本與其近鄰樣本的距離信息，關注的是樣本周圍的可分性，每個樣本的可分性都僅與距離其最近的樣本相關，因此該度量只能反映數據的局部結構特性，對于距離各個類別較遠的離群樣本，度量N2將無法刻畫其可分性。

(2) LSC

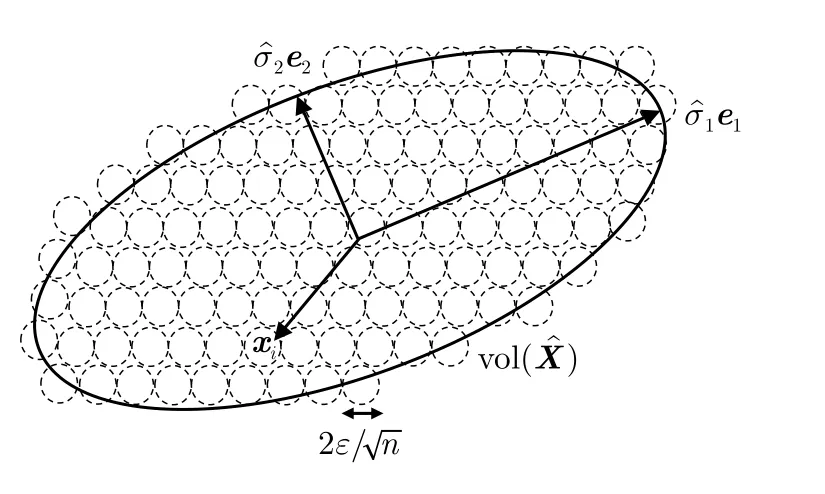
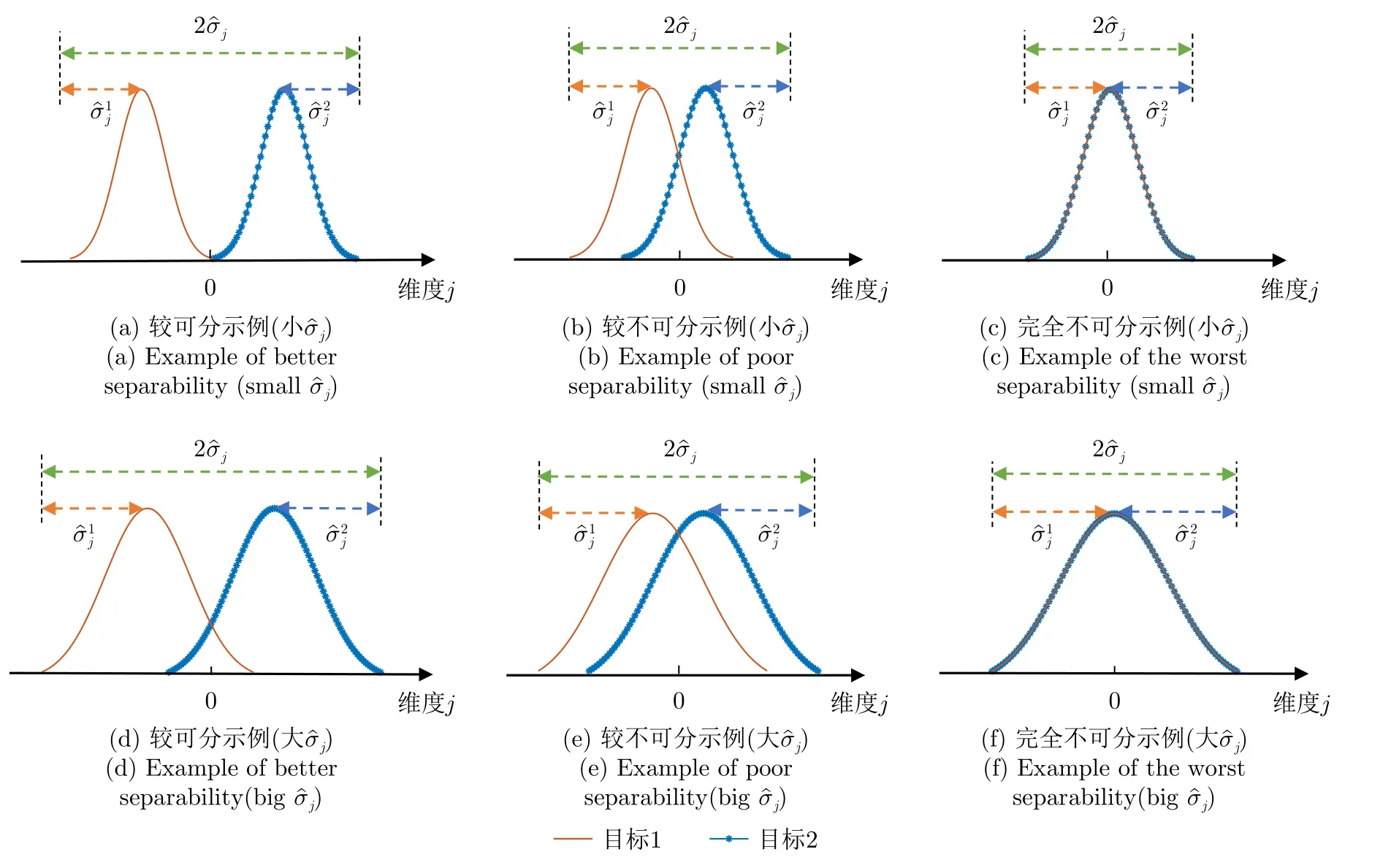
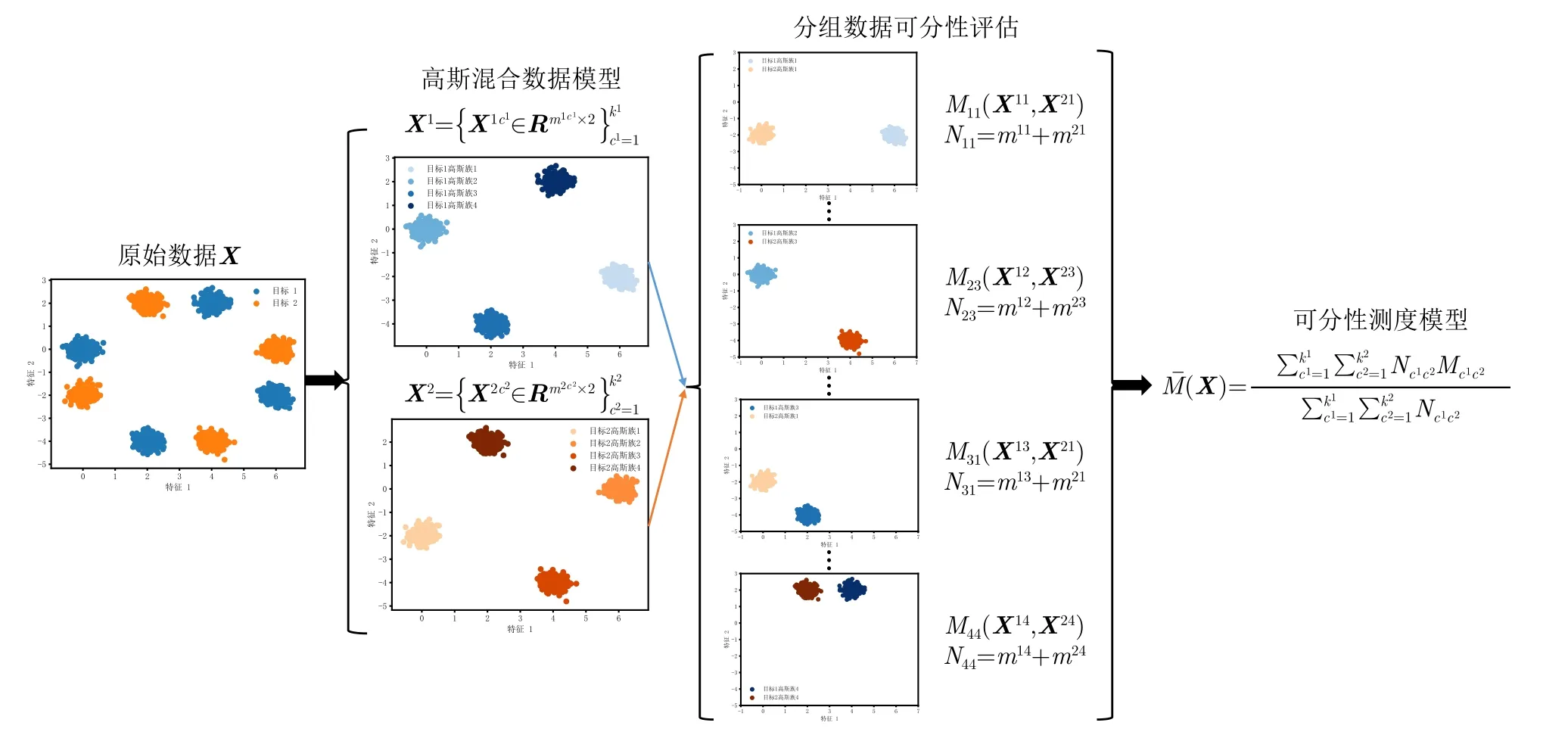
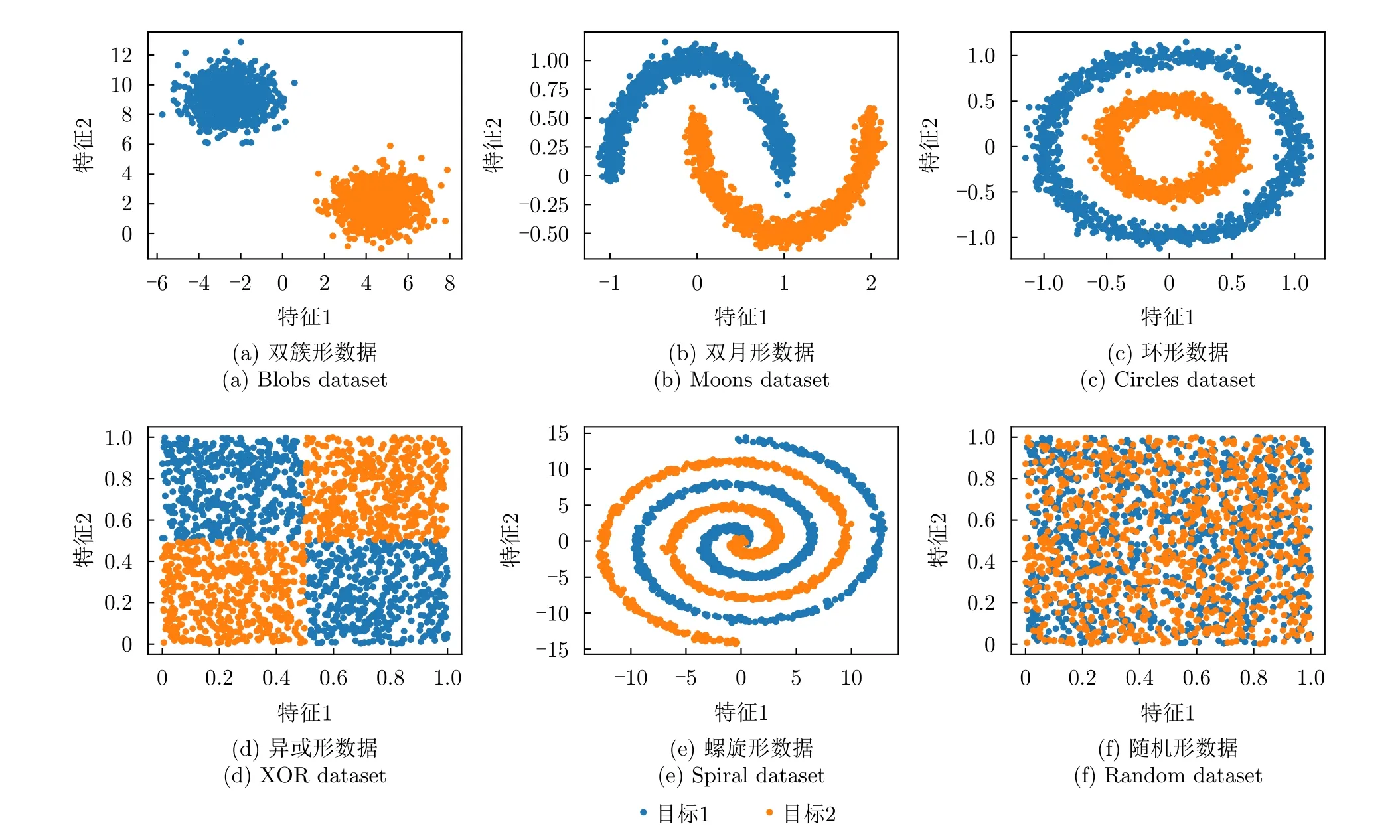
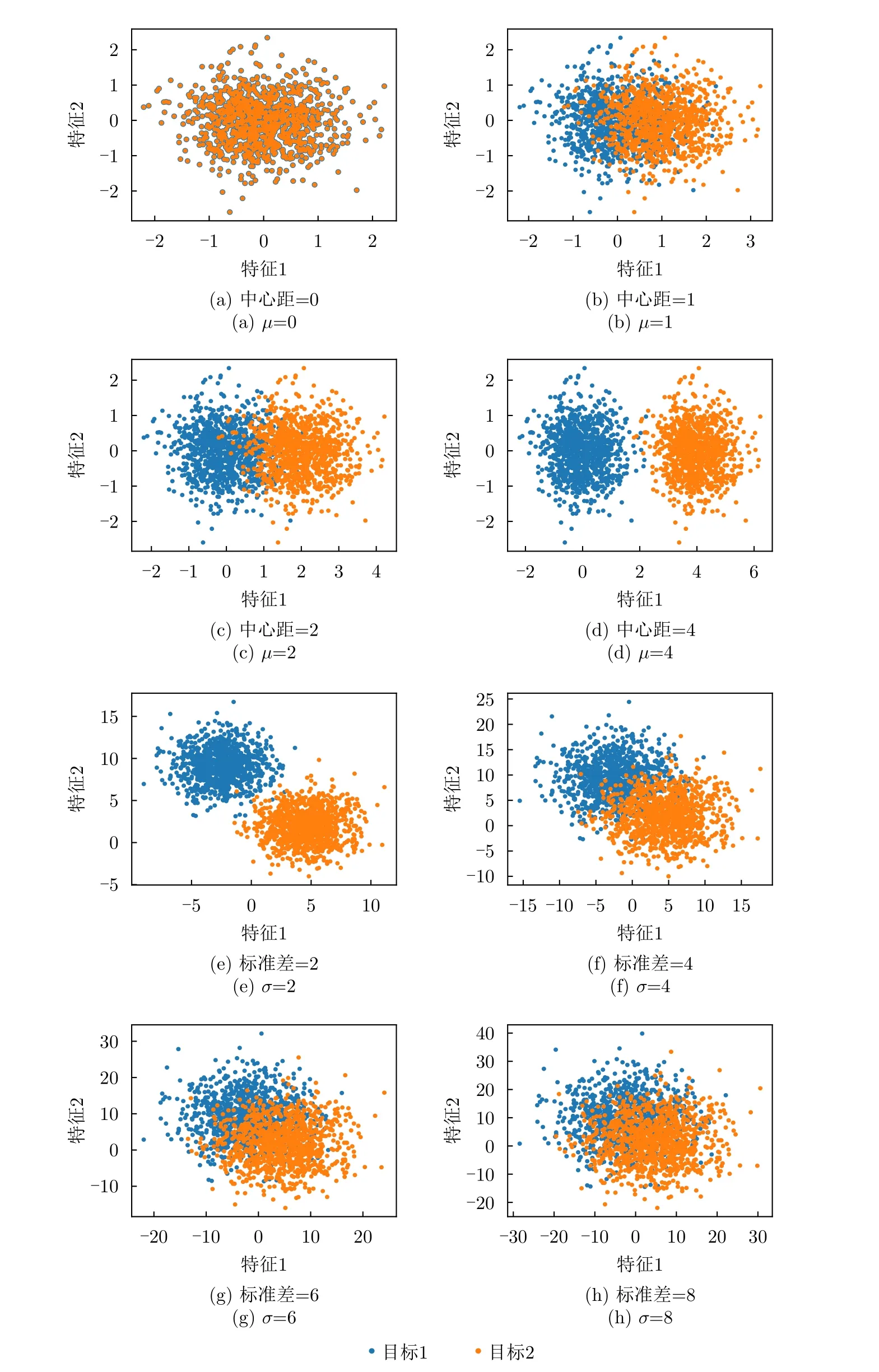
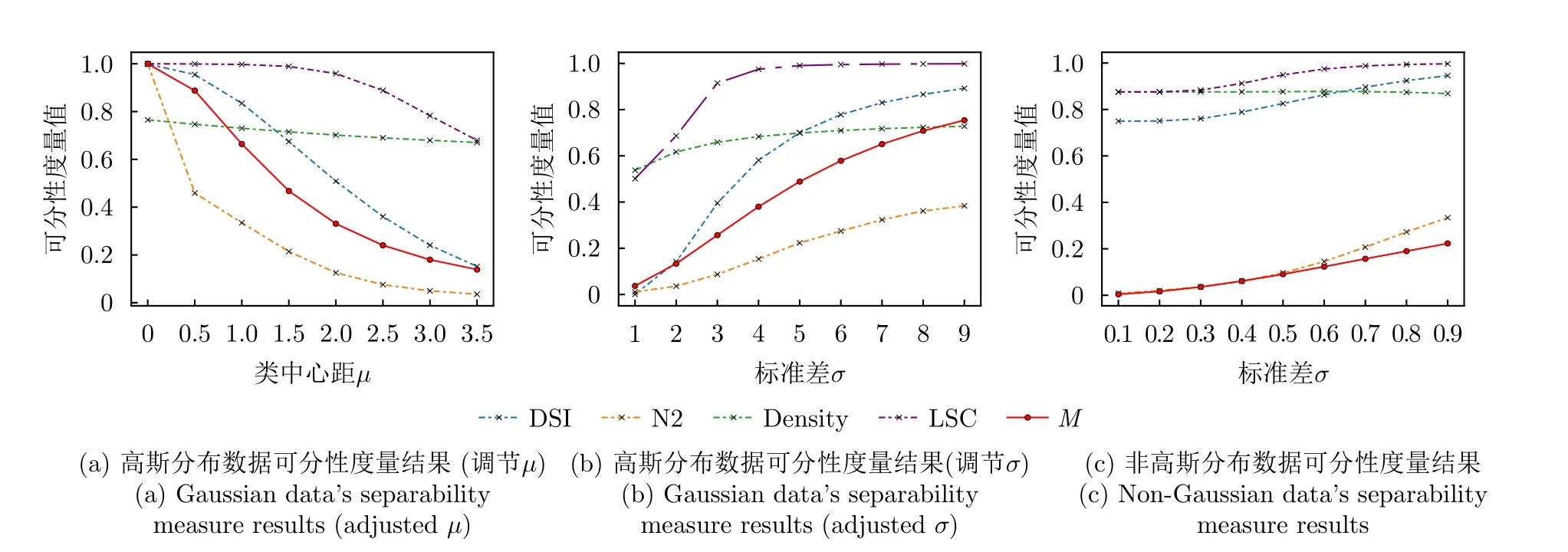
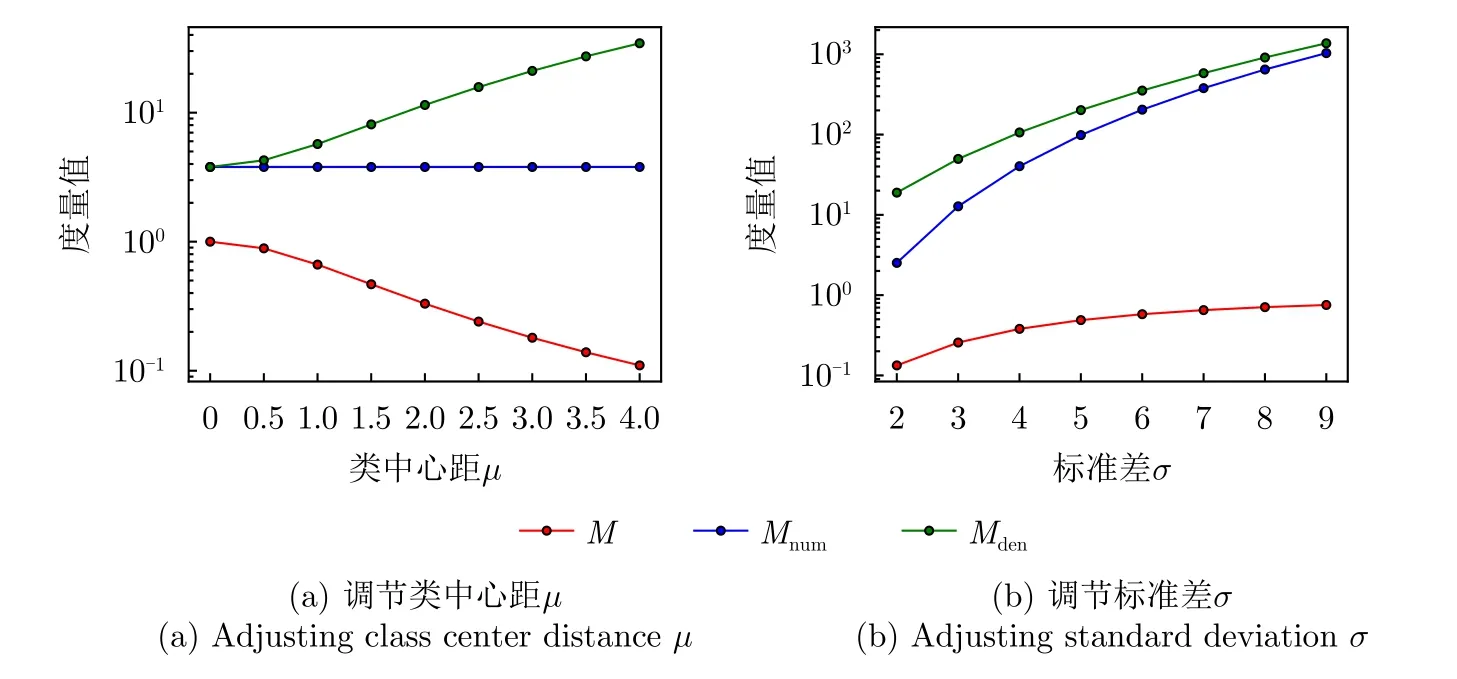
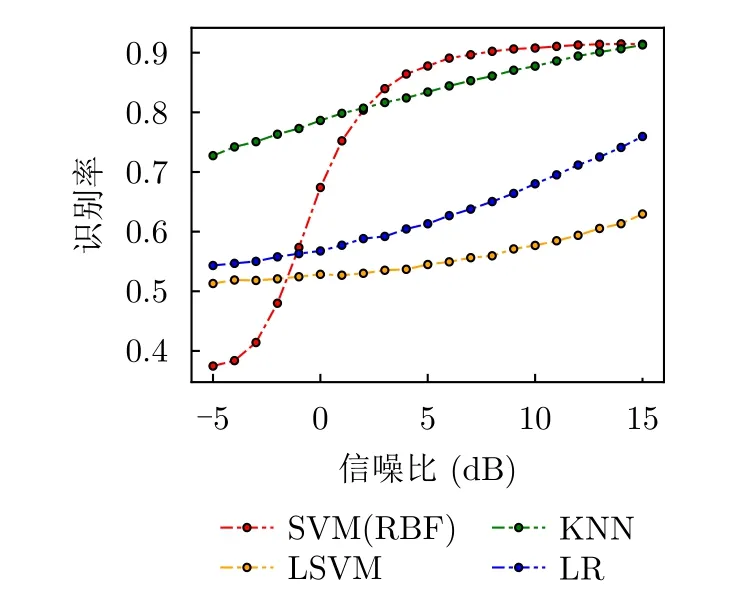
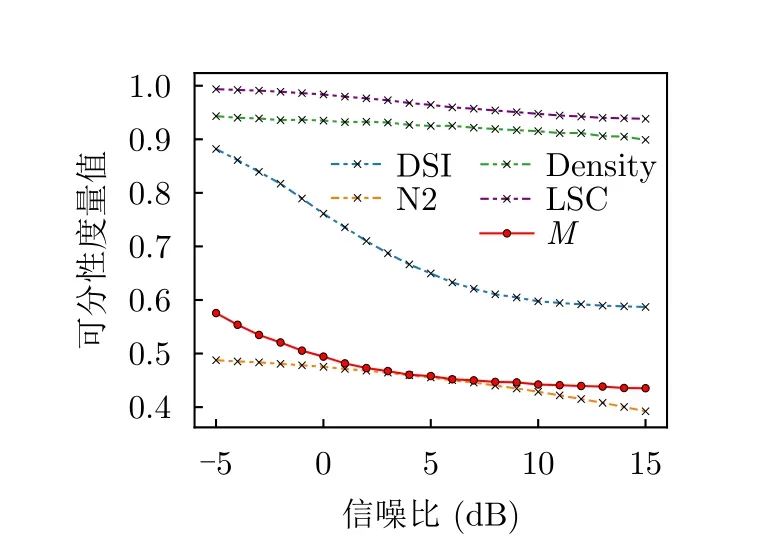
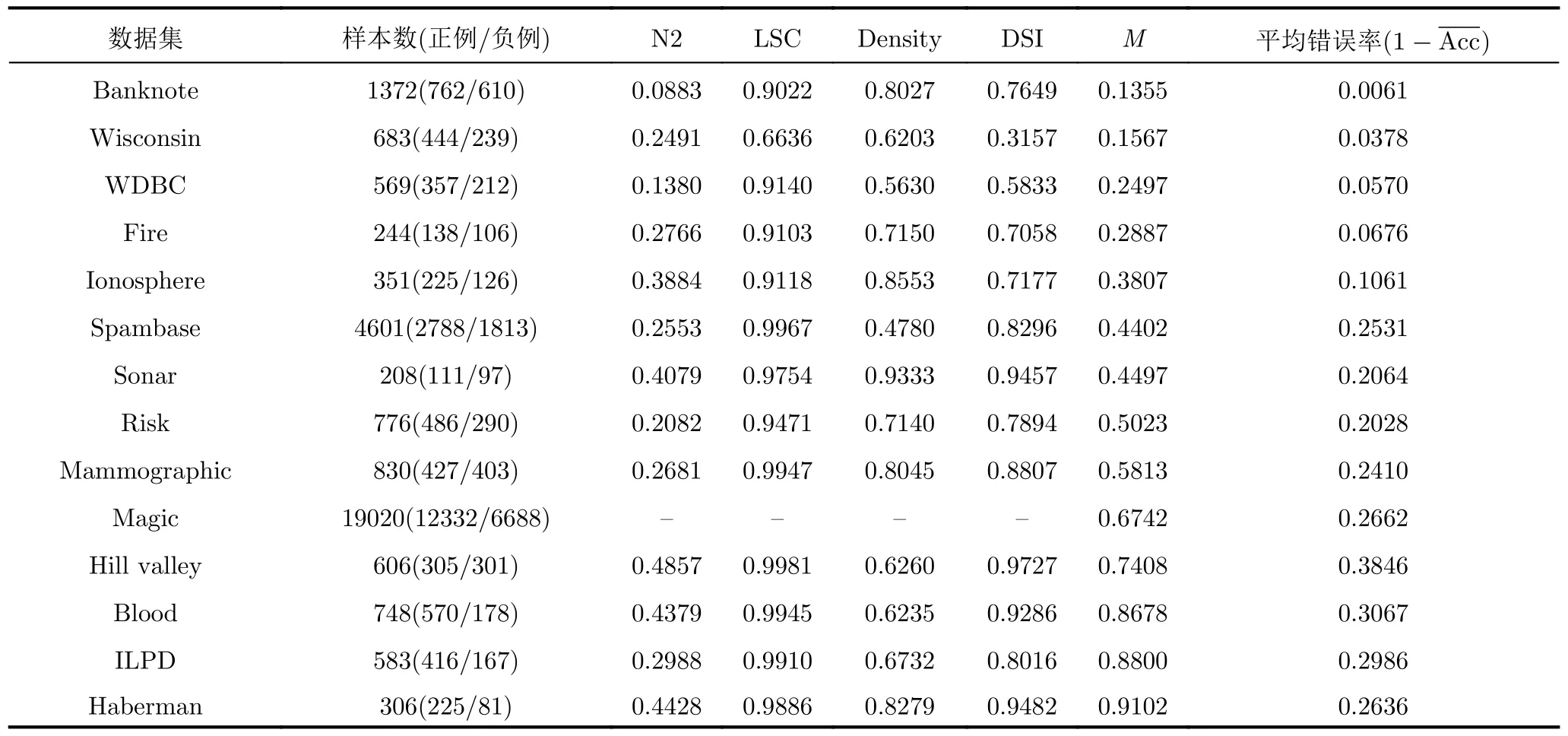
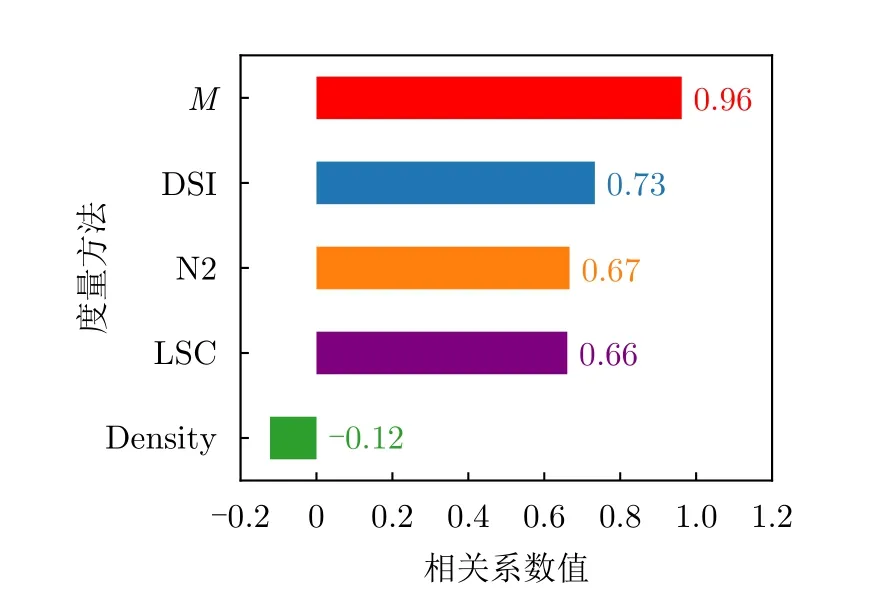
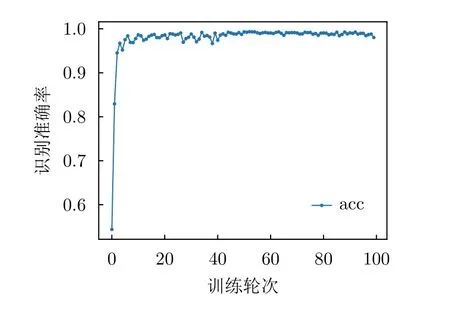
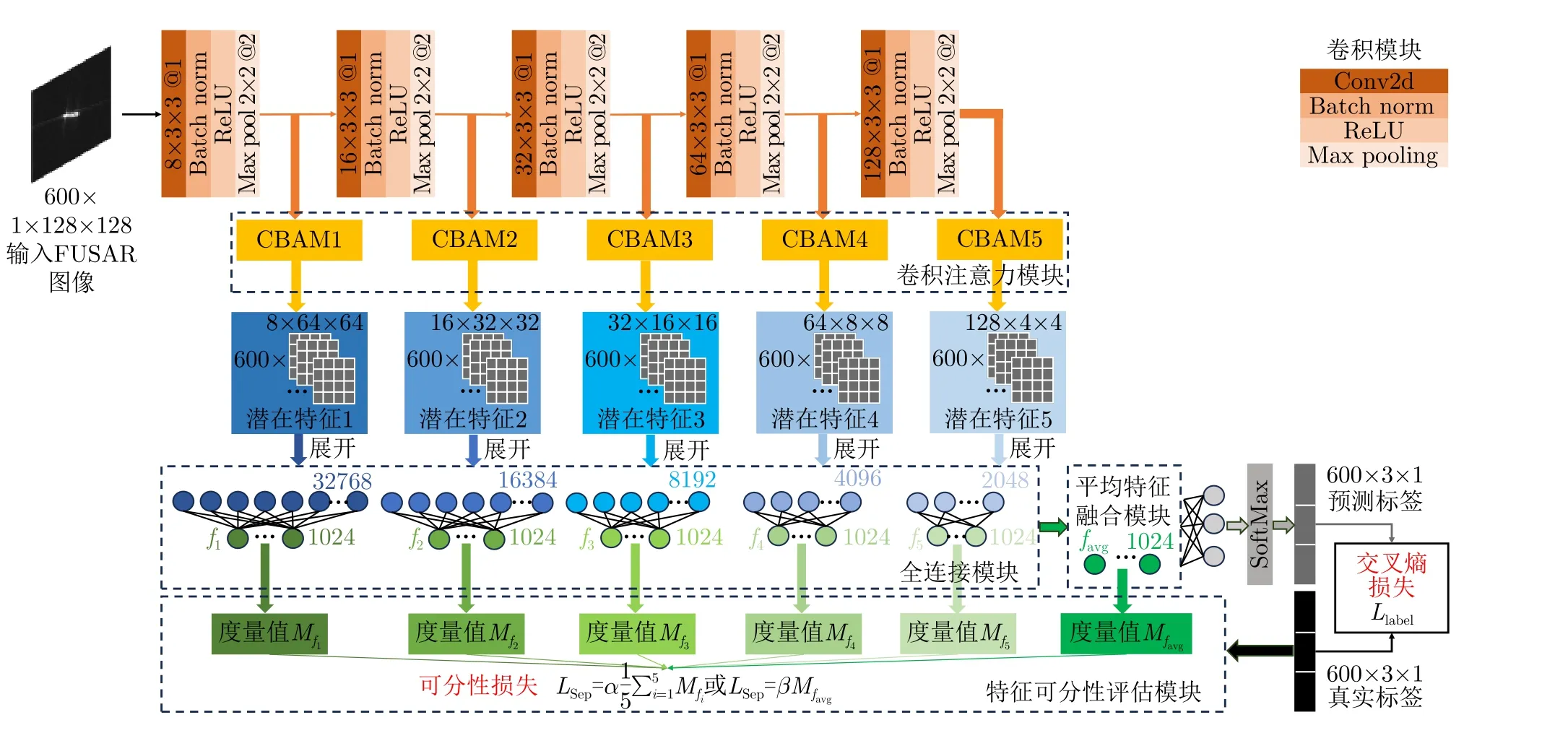
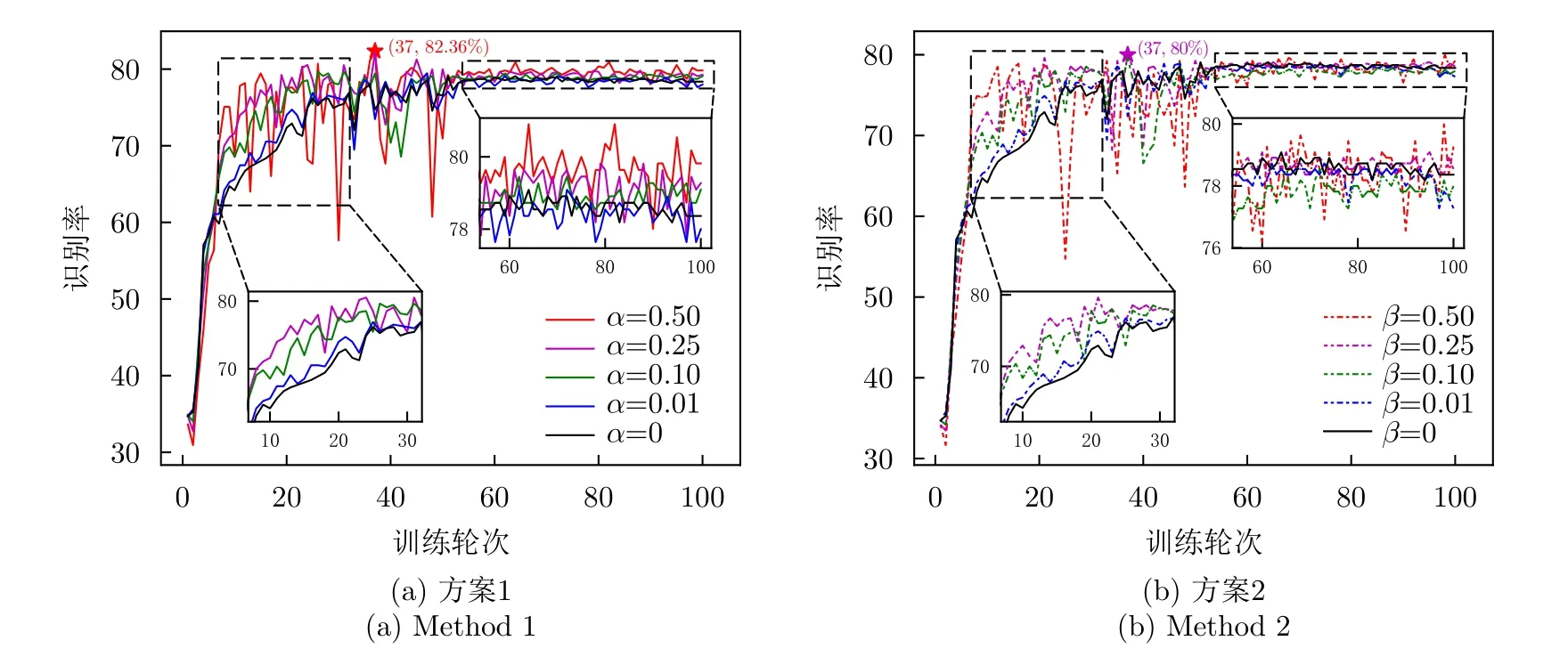
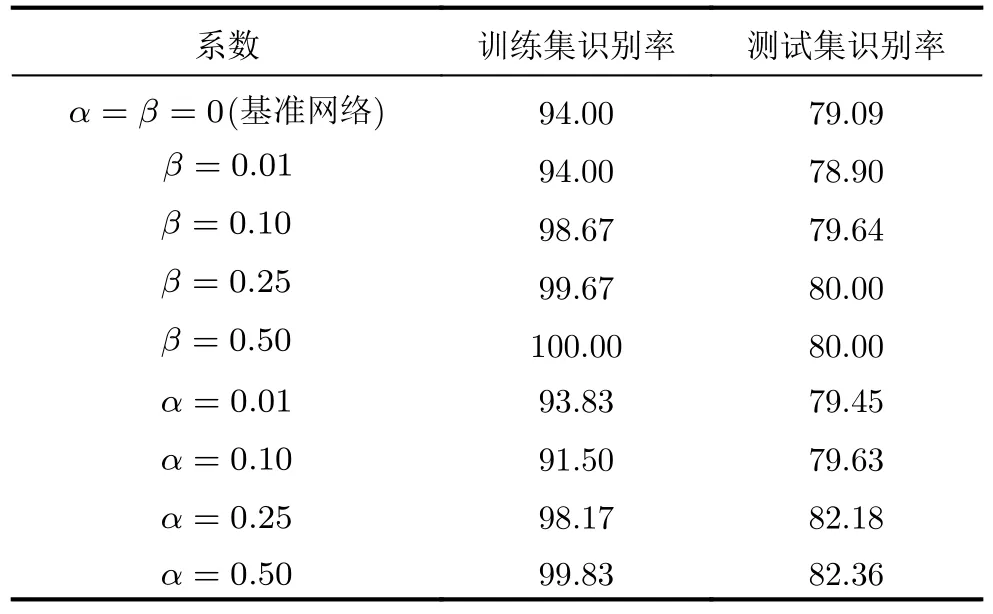
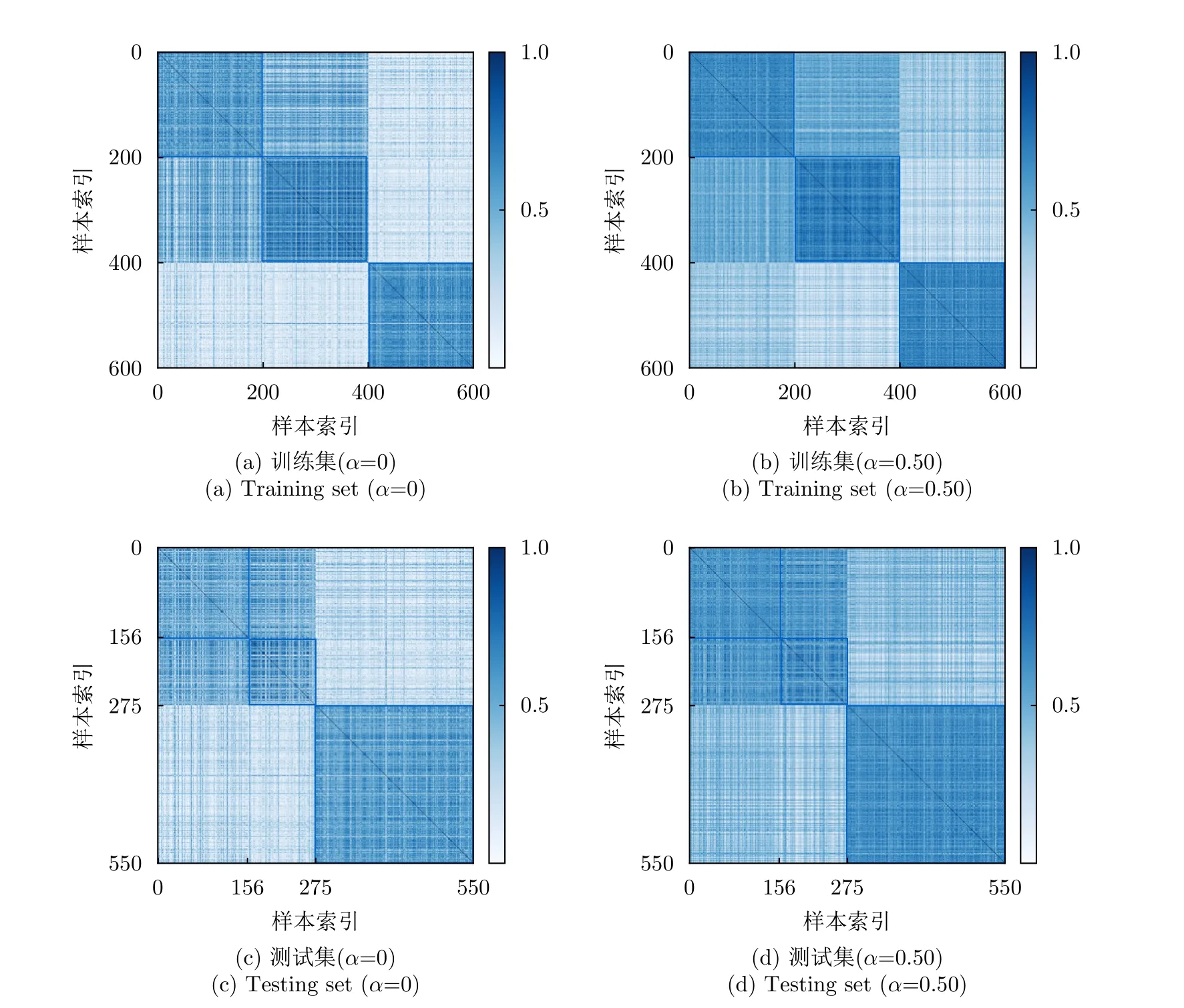
LSC度量方法設樣本xi與xj的距離為d(xi,xj)(i≠j)，xi到其最近鄰異類樣本N E(xi)的距離 為d(xi,NE(xi))，則| LS(xi)|定義為滿足條件d(xi,xj)

式(2)表明LSC賦予距離異類樣本更近的樣本更大的值，意味著其認為處于異類樣本分布中或處于決策邊界附近的樣本點導致可分性的惡化，因此更適用于度量決策邊界的復雜度。雖然LSC相對N2更多考慮了同類樣本距離信息，但對于異類樣本距離信息的利用僅限于最近鄰的異類樣本，異類樣本距離信息的缺失使得LSC度量僅是對數據可分結構的局部表征量。

(3) Density

Density度量方法首先將數據表示成網圖G=(V,E)的形式，網圖G中的V表示樣本，有節點數|V|=m，E表示樣本連接邊數，滿足0≤|E|≤m(m-1)/2，同類樣本xi與xj兩兩連接的條件是二者的距離小于給定閾值t，即d(xi,xj)

式(3)表明Density數值取決于網圖G中保留的邊數|E|，值越大表明數據越不可分。|E|的大小受到設定閾值t的影響，過大的t會產生近乎全連接結構的網圖，過小的t將產生稀疏結構的網圖，二者都將導致數據可分性判定的模糊。此外度量Density只利用了同類樣本的距離信息，其表示同類樣本緊密度，忽略了異類樣本距離對數據可分性的影響，因而對異類樣本距離變化不敏感。

(4) DSI

式(4)表明度量DSI充分利用了同類及異類樣本的距離信息，其對數據可分結構的描述更加全面，但文獻[13]的實驗表明該度量無法衡量決策邊界的復雜度。

上述方法存在統一的缺陷，即其都基于對樣本距離的計算，因此度量性能將會受到所選擇的距離函數的影響[29]。例如歐氏距離不適用于衡量高維數據的距離，這將導致基于歐氏距離計算的度量值無法比較具備不同維度的數據集可分性優劣。最后需要說明的是為了方便比較，各度量經數值轉換后的取值范圍都在0～1之間，且數值越小，表明數據的可分度越高。

3 率失真函數

率失真函數源于信息論中的編碼理論，它描述了在限定編碼誤差下對數據的最小編碼率[19]。當編碼誤差服從高斯分布時，零均值數據的最小編碼率具有易于計算的表達式[20]。率失真函數為

其中，數據X=[x1,x2,...,xm]∈Rn×m由具有n維特征的m個樣本構成；ε為給定的編碼誤差量；最小編碼率R(X)是關于數據X的率失真函數，具體表現為與X的協方差陣有關的對數行列式log2det(·)的形式，n階單位陣In×n的引入保證了方陣滿秩，其行列式不為零。log2det(·)的凹函數性質使得R(X)具有良好的優化特性。

此外，式(5)同時具有較好的幾何可解釋性，可以作為數據所在特征空間的緊性度量。原始數據X在其特征空間的容量 vol(X)，正比于其正交的奇異向量組[σ1e1,σ2e2,...,σnen]所張成空間的體積，在數值上轉化為數據奇異值σj的乘積，又等價于其協方差陣XXT的特征值λj的開方的乘積，如式(6)

式(8)反映了率失真函數的幾何意義，即數據的奇異向量所張成空間的體積可以由多維高斯分布單元填充的數量表示，二維數據的率失真編碼示意圖如圖2所示，其中高斯分布單元的半徑應當小于數據的最短主軸，有

圖2 二維數據的率失真編碼示意圖Fig.2 Schematic of 2D data’s rate distortion coding

4 基于率失真理論的數據可分性度量構建方法

4.1 單一維度的數據可分性分析過程

圖3 不同奇異值下的數據可分性示意圖Fig.3 Schematic of data separability under different singular values

4.2 高維數據可分性度量構建方法

將單一維度的數據可分性分析判別式向原始多維數據擴展，一個簡單的思路就是將各個維度的可分性分析過程級聯，由于數據的奇異向量相互正交，因此各個維度的可分性信息互不串擾，多維正交基下的數據可分性度量構建流程如圖4所示。

由 log det(·)的凹函數特性，可以證明度量M的取值邊界，其達到上界的充要條件為各類別的中心化數據具有完全相同的協方差陣，有定理1。

對于零均值多維高斯分布數據，當且僅當各類別協方差陣相等時，此時各類別數據具有完全相同的分布，數據處于完全不可分的狀態，度量M越趨近于1，數據越不可分。

4.3 非高斯分布數據可分性度量方法

由4.1節及4.2節，定義數據可分性度量的數學模型

文獻[30]在運用主動學習方法識別合成孔徑雷達目標數據集時，首先給出了如圖5原始數據X所示的樣例。原始數據X中，目標X1與X2在總的特征分布上具有較高的相似性，對于僅能產生線性超平面的分類器，該數據是完全不可分的數據集，運用上述度量也將相應得出M ≈1的結論。但數據X中，不同類樣本間的特征互不交疊且具有清晰的分隔邊界，這意味著數據是局部可分的，對于能產生非線性分隔平面的分類器，該數據是完全可分的數據集，因此數據的局部可分特性影響了非線性分類器的識別性能上限。本文提出非高斯分布數據可分性度量方法，考慮了數據局部可分特性，能夠真實地反映數據特征的重疊度，圖5為在仿真樣例的可分性度量模型構建示意圖。

圖5 非高斯分布數據可分性度量構建示意圖Fig.5 Construction schematic of data separability measure under non-Gaussian condition

對于具有任意類別數的數據集可分性度量過程總結如算法1所示。特別地，當高斯聚類數k=1時，算法的子過程退化為典型二分類高斯分布數據的可分性分析情形，此時多分類數據的可分性度量值為各二分類度量模型的加權求和，類似于機器學習分類器的一對一(One vs One,OvO)模型，本節所提度量更關注數據中屬于不同類別的樣本間的局部可分特性。

5 實驗驗證

為驗證所提度量的有效性，本文首先在二維仿真數據集上開展實驗，二維數據可分性的特點在于其能夠通過繪制特征散點圖的方式直觀地判定，因此當可分性度量值與直觀判定的可分性優劣相當時，認為度量有效衡量了數據可分性；此外，加噪數據可分性可以由仿真設置的信噪比預先判定，因此當可分性度量值的變化趨勢隨信噪比增大逐漸減小時，認為度量有效衡量了加噪數據可分性。接著在實測高維數據上開展實驗，由于高維數據可分性是非直觀的，因此通過分析度量與不同模型統計得到的平均識別率之間的相關性來驗證度量有效性，該實驗的目的在于運用可分性度量量化數據識別難度，為評估識別模型在批量數據集上的識別能力提供評判基準。最后運用可分性度量量化分析了卷積神經網絡各模塊提取特征可分性變化趨勢，進一步將所提度量作為特征可分性損失參與網絡訓練過程，達到優化特征質量的目的。上述實驗中，現有可分性度量DSI,N2,LSC和Density方法作為對比方法體現所提度量的優勢。

算法 1 平均意義下的數據可分性度量計算過程Alg.1 Average data separability measure computing

5.1 可分性度量有效性驗證實驗

由可分性度量方法評定的數據可分性優劣首先應當與現實可觀察的數據可分程度吻合，因此該節實驗主要驗證可分性度量在已知可分性優劣的二維仿真數據與加噪數據上的有效性。二維數據可分性可以通過可視化其特征散點圖的方式直觀地判定，因此本文構造了不同可分性優劣的數據集，其特征散點圖如圖6、圖7、圖8所示。圖6所示數據理想的決策邊界復雜度由圖6(a)-圖6(f)依次遞增，對應可分性依次遞減；圖7、圖8所示數據的類間重疊度由圖7(a)-圖7(d)、圖7(e)-圖7(h)、圖8(a)-圖8(d)依次遞增，對應可分性依次遞減。圖7與圖8的區別在于類內樣本是否能夠用同一個高斯分布表示，以檢驗度量方法對非高斯分布數據的適用性。加噪數據可分性可以由仿真設置的信噪比預先判定，設置信噪比范圍為-5 dB 到15 dB。

圖6 二維數據特征圖Fig.6 2D data’s feature map

圖7 不同類間重疊度的高斯分布數據集Fig.7 Gaussian data with different class overlap

圖8 不同類間重疊度的非高斯分布數據集Fig.8 Non-Gaussian data with different class overlap

5.1.1 決策邊界復雜性度量驗證實驗

具體地，依據圖6所示特征散點圖，可以觀察到數據圖6(a)可以由一個簡單的線性超平面正確劃分開，數據圖6(b)-圖6(f)的理想劃分面則需要更多線性超平面擬合得到，其不規則程度相對線性超平面而言依次遞增，因此各數據集的識別復雜度是由圖6(a)-圖6(f)依次遞增的。當可分性度量值由數據圖6(a)-圖6(f)順序遞增時，認為度量能夠有效衡量各數據集的可分性優劣。依次設置高斯聚類數k1=k2=[1,3,5,8]，則所提度量及對比方法在圖6所示數據的度量值總結如表1所示。

表1 典型特征圖可分性度量結果Tab.1 Separability measure results of typical feature

表1中，標灰的度量值表示對應行的度量方法無法有效衡量對應列數據的可分性。具體地，對于圖6所示的數據集，度量DSI無法區分數據圖6(b)與圖6(c)，這是由于其對決策邊界復雜度不敏感[12]；度量N2及Density則無法區分數據圖6(d)與圖6(e)，這是由于從樣本局部可分性的角度，度量N2認為圖6(d)中包含有更多與異類樣本更接近的樣本，度量Density則認為圖6(e)中同類樣本分布更加緊密，從而得出了與判定決策邊界復雜度相反的結論；所提度量在k=1時主要衡量數據線性可分度，表明圖6(c)-圖6(f)均為線性不可分數據，在k=3時利用數據局部線性可分度信息還不夠充分，因此仍無法區分螺旋形與混合形數據，上述表明僅利用樣本局部可分性的度量方法對數據整體可分結構的描述還不準確。實驗表明僅度量LSC與(k>3)能夠有效對比圖6數據集的可分性優劣，這是由于度量LSC更關注決策邊界附近的樣本，而隨著聚類數k的增加，所提度量對各數據集可分性優劣對比結果趨于穩定，其通過數據高斯分塊的方式，結合基于率失真理論構造的可分性度量M，統計局部線性可分度，實現對數據全局非線性可分度的評估。

5.1.2 類間重疊度度量驗證實驗

制約分類器識別性能的因素之一是數據類間重疊度。圖7、圖8展示了不同類間重疊度的二分類數據集，每個數據由幾族高斯分布采樣2000個樣本得到，類間重疊度則通過設置標準差σ或類中心距離μ調節，共同構成待評估數據集合。圖7的數據集類內樣本服從典型高斯分布，圖8數據集的類內樣本則呈現混合高斯分布的形式。對高斯分布數據設置兩組實驗，分別設置標準差σ ∈[1:1:9]與類中心距μ∈[0:0.5:4] ；對非高斯分布數據，設置σ ∈[0.1:0.1:0.9]。運用度量M,(k1=k2=4)及現有對比方法，度量結果如圖9(a)、圖9(b)、圖9(c)所示。

圖9 不同類間重疊度的數據可分性度量結果Fig.9 Separability measures for datasets with different class overlap and dimensions

圖9(a)中，各可分性度量值均隨著類間距的增加逐漸下降，變化趨勢均符合觀察到的事實：類中心距越遠(μ越大)，類間重疊度越小，數據越可分。但各方法在該測試樣例上的動態變化范圍各不相同，可以看到當兩類目標完全重疊(μ=0)時，度量M,DSI,N2,LSC均等于1，達到其上界，代表數據最不可分的情況，而Density等于0.765，取值無法反映最不可分數據集的可分性。當μ由0增加到1.5時，類間重疊度顯然減小，對應到LSC上卻沒有明顯的變化趨勢，而N2在μ由0增加到0.5時出現了陡然的下降趨勢，但此時類間重疊度變化是微小的。圖9(b)中，LSC在σ=6時取值為1達到其上界，但由圖7(g)數據此時還不是完全不可分的；其余可分性度量值均隨著類內分散度的增加而逐漸上升，變化趨勢均符合圖7觀察到的事實：同類樣本越分散(σ越大)，類間重疊度越大，數據越不可分。在圖9(a)、圖9(b)實驗中，僅M與DSI在兩類目標由完全重疊到完全分離過程中，表現出最大動態變化范圍，且變化趨勢更加平滑。圖9(c)中，僅M,DSI,N2隨σ增加而逐漸增大，但DSI將未交疊非高斯數據(圖8(a))判定為可分性很差的數據集，度量值為0.75，但事實上對于K近鄰等能產生非線性決策邊界的識別器而言，該數據集是完全可分的。

在上述3個實驗中，LSC無法區分類間重疊度已經達到一定量級的數據可分性；Density更多衡量同類樣本緊密度，因此在圖9(c)中由于同類樣本隨σ增加逐漸靠近，從而在數值上表現出可分性漸好的趨勢；僅M,DSI,N2隨著不同類樣本交疊量的增加均表現出正確的變化趨勢；但DSI無法衡量具有非線性劃分結構數據的可分性；所提度量M具有更大的動態變化范圍，且相對N2更加平滑(圖9(a))，能夠有效衡量高斯或非高斯數據的類間重疊度。

為進一步解釋所提度量M的工作機理，圖10給出圖7實驗場景中作為M分子的類內分布散度Mnum和作為分母的整體分布散度Mden的變化趨勢。圖10(a)表明當μ變 化時，Mnum保 持恒定，Mden起到主要的可分性度量作用，說明整體分布散度中包含數據的均值差異信息；圖10(b)中隨著σ的增加，Mnum與Mden同時上升，Mden逐漸逼近Mnum，對應類間重疊度增加，表明Mnum與Mden的相對數值能夠有效衡量數據類間重疊度。

圖10 整體分布散度與類內分布散度變化趨勢Fig.10 The trend of overall and intra-class distribution divergence

5.1.3 加噪數據可分性度量驗證實驗

本節實驗模擬真實目標識別噪聲環境，通過將模型訓練在原始數據測試在批量加噪數據上以評估其性能，同時驗證度量在加噪數據上的有效性。理想的識別模型是其在所有加噪數據上的識別率都一致高于其他模型，但在實際性能比對實驗中，更一般的現象是模型在不同加噪數據上的識別率各有高低，這導致性能評估模糊問題。以表2中數據WDBC為例，構造信噪比-5 dB 到15 dB的加噪數據，SVM(RBF),KNN,LSVM,LR的識別率結果反映了上述問題，如圖11。

表2 識別模型識別率結果Tab.2 Recognition accuracy results of recognition models

圖11 不同信噪比條件模型識別率表現Fig.11 Different models’ accuracy under various condition

圖11中KNN在各信噪比數據上的識別率一致地高于LR，而LR又一致地高于LSVM，可以得出三者抗噪性能的對比結論：KNN >LR >LSVM。但由該圖無法得出SVM(RBF)的性能評估結論，SVM(RBF)在信噪比高于3 dB時一致地優于其他模型，信噪比低于-2 dB時性能最差。雖然可以通過對比各信噪比數據上的平均識別率來判定模型性能優劣，但平均識別率忽略了各數據集的識別難度差異，直觀上更難識別的任務應當被賦予更大的權重，因此通過可分性度量量化識別難度，為識別率賦權提供依據，加噪數據可分性度量結果如圖12。

圖12 加噪數據可分性度量結果Fig.12 Separability measure results of noisy data

圖12中僅Density數值隨信噪比上升存在微弱的起伏，說明其度量精度較差。DSI雖具有最大動態變化范圍，但圖11中大部分模型的識別率變化趨勢緩慢，說明各任務間識別難度差異并不十分顯著，且當信噪比為 15 dB時模型識別率與表2中在原始數據的測試結果還存在一定差距，說明此時可分性數值也仍存在一定差距，但DSI數值已經接近對原始數據可分性度量結果0.5833。所提度量M具有合適的動態變化范圍，且信噪比為15 dB時值為0.4352，與原始數據度量值0.2497還存在一定差距，綜合表3的實驗結果所提度量M更能真實地反映數據可分性。

表3 實測數據集可分性度量結果Tab.3 Separability measure results of real data

5.2 基于可分性度量的數據識別難度評估實驗

在數據集發布與構建相關的文獻[31,32]中，通常運用公開通用的識別模型如支持向量機、經典深度神經網絡架構等檢驗構建數據集的適用性，用識別結果分析數據可分性。然而使用的識別模型不同，識別結果存在明顯差異，無法描述數據固有可分特性，因此本節基于可分性度量評估數據識別難度。此外數據識別難度評估的需求還源于目標識別評估中的具體問題：如何從在各個識別任務上識別率各有高低的眾多識別器中選出識別性能最優的模型。為直觀展現上述問題，本節選擇4種識別器：運用徑向基核函數(Radial Basis Function,RBF)的支持向量機(Support Vector Machine,SVM)、K近鄰(K-Nearest Neighbors,KNN)、線性SVM和邏輯回歸方法(Logistic Regression,LR)，在表2所示的14個二分類實測數據集上[25]測試模型，測試過程中訓練集與測試集按照7/3的比例劃分。表2給出數據集樣本總數、相應的正負例數及特征數，各模型在各數據上的識別率，“√”表示其在對應行數據上識別率最高，“×”表示最低，平均識別率為4種識別器在同一數據上識別率的平均值，文獻[6]表明其可以作為側面反映識別難度的參考值。

表2首先可以直觀地反映以下問題：(1)同一種模型在不同數據上的識別率各不相同，變化的識別率無法作為衡量模型識別能力的固有屬性。(2)不同模型在同一數據上的識別率各不相同，且有時會出現較大差距，如 LSVM在Hill valley上的識別率為0.9670，而SVM(RBF)為0.4780，變化的識別率無法作為衡量數據識別難度的固有屬性。(3)平均識別率在一定程度上可以反映數據識別難度，但其有效性基于運用大量識別器開展統計實驗，并且無法客觀描述樣本數分布不均的數據集如Blood,ILPD,Haberman的識別難度。(4)在不同數據上模型識別率高低對比結果各不相同，如SVM(RBF)在Banknote,Ionosphere,Magic,Blood上識別率最高，而在Wisconsin,Fire,Hill valley上識別率最低，導致無法得出統一的性能優劣評估結論。

為解決依賴識別率評估產生的性能比對模糊問題，考慮到數據固有可分特性對識別性能的影響，本節利用可分性度量方法評估數據識別難度，由量化的識別難度為識別任務標定基準，進一步可以考慮構建以識別難度為參數的識別率到模型識別能力的函數映射模型，得到表示模型固有識別性能的固定表征量。本文工作重點在于驗證所提度量方法的有效性，14個數據集可分性度量結果如表3所示，其中平均錯誤率作為參照指標之一，各指標值越大表示數據越不可分。在排除樣本數分布不均的數據集Blood,ILPD,Haberman后，平均錯誤率作為不同模型對同一數據識別結果的統計量對可分性的衡量具有一定的參照意義，因此通過分析各度量值與平均錯誤率之間的相關性驗證度量有效性，繪制各度量值與平均錯誤率之間的皮爾遜相關系數如圖13，同時繪制度量與平均錯誤率曲線圖如圖14。

圖13 可分性度量與平均錯誤率相關性矩陣Fig.13 Correlation matrix between separability measures and average recognition error

圖14 可分性度量與平均錯誤率曲線Fig.14 Curves between separability measure and average recognition error

相關系數的取值在-1到1之間，取值為正表示變量之間是正相關，為負表示負相關，其絕對值越大表示變量之間的線性相關性越強。圖13中，所提度量M與平均錯誤率的相關系數為 0.96，具有最大的線性正相關性，表明隨著M逐漸增大，數據變得越來越不可分，對大多數識別器而言識別性能下降，錯誤率隨之提升。表現最差的度量為Density，其與錯誤率的相關系數為-0.12，說明同類樣本緊密度并不足以衡量可分性。LSC,N2,DSI與平均錯誤率仍具有一定的正相關性，相關系數值分別為0.66,0.67,0.73，說明其也具備一定衡量可分性的效能，因此對于樣本數分布不均的數據，則可以通過比對M與N2,DSI的判定結果來分析M是否有效。例如表3中樣本分布不均的Haberman數據，平均錯誤率已不能客觀反映其與Mammographic的可分性差異，但通過與LSC,N2,DSI對照，表明M仍能夠正確地判定Haberman為可分性較差的數據集。圖14中，所提度量M數值與平均錯誤率基本對應，越小的M代表識別難度越小，對應低平均錯誤率；對比方法均存在較大的振蕩幅度，而M僅在數據Spambase和Sonar之間出現微小的振蕩，說明二者的識別難度相當，而平均識別率的統計誤差導致了這一現象。

相較于依賴大量模型統計識別結果的錯誤率指標，所提度量M獨立于模型識別過程，對數據固有可分特性描述更加本原，度量值更加客觀。此外在計算量上M相較對比方法也具備突出的優勢，對于具有m個樣本的n維數據，M的計算量在于兩次協方差陣行列式的計算，協方差陣的規模為n×n，當m>>n時如表3數據Magic，對比方法則需要建立19020×19020的距離矩陣而帶來巨大的存儲負擔，且導致運算效率低下，M則只需要計算兩次10×10規模矩陣的行列式，在存儲空間和運行時間上都大大優于對比方法。

5.3 基于可分性度量的識別網絡特征質量評估實驗

深度學習識別模型具有提取數據高維可分特征的能力，本節實驗首先探究深層卷積神經網絡中，隨著網絡層次的加深及訓練輪次的迭代，各卷積層所提取特征可分性與模型識別率相對應的變化趨勢特點，從特征可分性角度定量化解釋神經網絡有效工作的原因。進一步地，本節將所提可分性度量作為網絡損失函數的一部分，優化網絡學習到的特征質量，探究特征可分性對提升網絡識別性能的實質性作用。

本節采用合成孔徑雷達(Synthetic Aperture Radar,SAR)圖像數據集，包含標準工作條件下的MSTAR數據集[33]和復旦大學發布的FUSAR數據集[32]。其中本文構造的三分類FUSAR數據集包含樣本量較多的貨船、漁船和其余船只目標，3類船只包含相同的訓練集樣本量，以保證訓練過程的類平衡性。表4總結了SAR數據集相關參數。

表4 SAR圖像數據集Tab.4 SAR image datasets

本節首先在MSTAR數據集上評估文獻[34]提出的卷積神經網絡模型，網絡結構及可分性分析模塊如圖15所示。其中原始SAR圖像經過4個卷積模塊映射到可分的特征空間，為了減小可分性分析的計算量，在張量展開步驟之前對映射特征統一采用了2 ×2的自適應平均池化操作，最終各層得到的特征維度分別是64,128,256及512維 。網絡在MSTAR測試數據集上的識別率acc如圖16所示，經卷積模塊所提取特征的可分性度量結果分別如圖17所示，圖17由左至右分別是模塊1至模塊4提取特征可分性分析結果和各層可分性對比結果，由上至下分別對應Density,DSI,LSC,N2,M度量方法。

圖16 網絡在MSTAR數據上的識別準確性能Fig.16 Recognition accuracy performance of the network on MSTAR datasets

圖17 MSTAR數據集特征可分性度量結果Fig.17 Feature separability measure results for MSTAR dataset

由圖16僅能得出網絡在MSTAR測試數據上以較少的訓練輪次就達到了較高的識別率，但無法從中解釋神經網絡有效工作的具體原因，因此將各模塊提取特征可分性評估引入識別評估過程。圖17可以得出模型之所以在輸出端表現出優異的識別性能是由于組成神經網絡的各個模塊都提取到了逐漸可分的目標潛在特征，在實驗現象上表現為隨著網絡深度的增加，所提取特征均呈現越來越可分的趨勢，數值上有ML1>ML2>ML3>ML4，并且隨著迭代輪次的增加，特征可分性漸高，預示著識別率的提升；特征可分性收斂，預示著識別率的飽和。圖17同時比對了本文所提方法與對比方法對特征可分性的度量結果。Density的度量性能最差，隨著訓練輪次的增加，各層度量值呈現發散的趨勢，且無法區分第2～4層特征可分性優劣；其余方法均能夠區分各層特征可分性的優劣，數值上表現為DSIL1>DSIL2>DSIL3>DSIL4,LSCL1>LSCL2>LSCL3>LSCL4,N2L1>N2L2>N2L3>N2L4，可以體現越深層網絡提取的特征越可分，但所提度量M相比對比方法具有更加平滑的收斂趨勢，且各層可分性度量值的數量級差距更大，說明M對特征可分性的變化更為敏感。從模型性能優化的角度，將M作為損失函數的一部分，迭代過程中同時優化特征可分性，能夠快速引導模型學習到更加可分的特征，從而提高模型識別性能。

進一步地，本節在文獻[35]提出的骨干網絡中加入特征可分性度量損失，在FUSAR數據集上探究所提可分性度量對網絡識別性能提升的實質性作用。帶有特征可分性度量約束的卷積神經網絡組成如圖18，其中包含用于特征提取的卷積模塊、卷積注意力模塊(Convolutional Block Attention Module,CBAM)、全連接模塊，用于特征融合的平均特征融合模塊，以及用于評估特征質量的特征可分性評估模塊。網絡損失函數由評估預測標簽與真實標簽差距的交叉熵損失和評估特征質量的可分性損失構成。考慮到識別性能與網絡各層特征及融合層特征都密切相關，故損失函數L有式(17)與式(18)兩種方案。

圖18 特征可分性度量約束下的卷積神經網絡Fig.18 Convolutional neural networks with feature separability constraints

其中，LLabel表示交叉熵損失，Mfi,Mfavg的形式如式(11)，分別表示第i個特征提取模塊的特征fi與平均特征favg的可分性度量，favg為fi(i=1,2,...,5)的平均值，α,β為可調比例系數。式(17)與式(18)兩種訓練方案在訓練集上交叉熵損失表現如圖19，在測試集上的識別率表現如圖20。

圖19 訓練集上交叉熵損失表現Fig.19 Cross-entropy loss performance on the training set

圖20 測試集上的識別率表現Fig.20 Accuracy performance on test set

圖19中，α=β=0表示訓練時不加特征可分性約束的基準網絡在訓練集上的損失函數表現，可以看到隨著可分性比例系數α或β逐漸增加，訓練集上的交叉熵損失以更快的速度收斂到了更低的值，增強了對訓練數據預測標簽與真實標簽之間的擬合效果。此外對比方案1與方案2的性能，當α或β均較小時，二者性能相當，交叉熵損失曲線基本重合；隨著α與β逐漸增加，相同比例系數的方案2相較方案1對訓練集具有更好的擬合效果。圖20展現了兩種方案在測試集上的識別率表現，可以看到當α或β取0.01,0.10或0.25時，識別率曲線在訓練初期(10～30輪次)能夠相較基準網絡達到更高的識別率，且α或β越大，提升效果越明顯。當α或β取0.50時，識別率曲線出現了明顯的振蕩，但在整個訓練過程中最高識別率相對基準網絡仍有明顯的提升。此外對比兩種方案的性能，方案1在α=0.50時，第37輪達到了82.36%的識別率，方案2在α=0.25及α=0.50時分別在第37輪及第98輪達到了80%的識別率。而在訓練的收斂階段(60～100輪次)，方案1相較方案2在α=β=0.50時能夠相較基準網絡有明顯的識別率提升。上述表明方案1在測試集上的泛化性能優于方案2，將網絡各層特征可分性度量作為損失函數的一部分對特征可分性加以約束，能夠優化網絡訓練過程，并且改善網絡在測試集上最終的識別率表現。表5給出不同α與β數值下的兩種方案在測試集上最優識別率表現，對應給出訓練集上的識別率。其中隨著α或β的增加，訓練集識別率均有不同程度的提升，方案1在訓練集上擬合性能雖稍劣于方案2，但其在測試集上泛化性能明顯優于方案2，具體表現在方案2β=0.50的測試識別率相對基準網絡約有0.91%的提升，方案1α=0.50時則有3.27%的提升。

表5 不同可分性系數下最優識別率表現(%)Tab.5 Optimal accuracy performance with different separability factors (%)

此外可分性度量對網絡識別性能的提升不僅體現在識別率上，還體現在其能夠引導網絡提取到更可分的特征。從可視化的角度分析特征可分性，本節采用樣本間余弦相似度矩陣及t分布隨機近鄰嵌入(t-distributed Stochastic Neighbor Embedding,t-SNE)，其中余弦相似度矩陣圖的行列表示樣本索引，已按照樣本所屬類別排序，兩個樣本余弦相似度越大表示二者越相似。圖21與圖22分別給出表5中基準網絡與α=0.50的可分性約束網絡最終層提取特征的樣本間余弦相似度矩陣及t-SNE圖。可以看到相對基準網絡，α=0.50時訓練集和測試集上類內樣本余弦相似度都有顯著的提升，而類間樣本余弦相似度雖然在第37輪迭代中沒有理想的下降趨勢，但在圖21(b)的訓練集中其數值顯著小于類內相似度，相較圖21(a)，類間與類內相似度比值存在下降趨勢，從而提升了特征可分性。而圖21(d)測試集上的可分性改善還在一定程度上受其與訓練集模板相似度的影響，因此對特征可分性優化效果不如圖21(b)顯著。由于t-SNE降維方法傾向于聚合相似度較高的樣本，圖21也表明加入可分性損失后，類內樣本相似度普遍高于類間樣本，因此在圖22(b)與圖22(d)中更為相似的類內樣本優先被聚合，從而表現出更高的類內聚集形式以及更加清晰的理想決策邊界。通過本實驗表明所提度量能夠有效地衡量網絡提取特征變化趨勢，將特征可分性度量作為網絡損失函數的一部分進行優化，能夠快速引導網絡學習到更可分的特征，從而提升識別性能。

圖21 最終層輸出特征樣本間余弦相似度矩陣Fig.21 The cosine similarity matrix between feature samples output from the final layer

圖22 最終層輸出特征t-SNE圖Fig.22 The t-SNE visualization of the feature output from the final layer

6 結論與展望

數據可分性度量為分析和評估識別模型性能提供了一種基準，在賦予了數據可分性的條件下，更能客觀地評價識別模型性能。本文基于率失真理論構建可分性度量模型，其描述了數據整體分布散度與類內分布散度的相對關系，綜合了樣本分布在各個正交特征維度的可分性信息。實驗表明，設計的度量方法通過結合高斯混合模型能夠衡量非高斯數據可分度；所提度量可以比較具備不同維度的數據集可分性優劣，其數值與經不同模型統計得到的平均識別率有強相關性，能夠作為數據識別難度的量化值，為識別結果預先提供評判基準；并且能夠評估神經網絡各卷積模塊提取可分特征的貢獻度，在測試階段作為網絡提取可分特征的評估指標，在訓練階段作為網絡提取可分特征的優化指標。

本文是對數據可分性研究的初步探索，仍有許多值得進一步深入開展的研究工作，包括針對具體識別任務特性與考慮數據更多分布特性的可分性度量設計，探究可分性度量與識別性能上限的對應關系，解釋識別網絡各層特征可分性之間的關聯等。總的來說，數據可分性度量作為直接面向數據的評估指標，與面向模型的準確性指標相結合，為雷達目標識別評估提供了一個新的評估視角，對識別模型實用化改進具有指導性意義。