城市排水管網外水診斷中特征因子的選擇

姚 俊，王 慶，2

（1.中電建生態環境集團有限公司，廣東 深圳 518101；2.中電建水環境科技有限公司，廣東 深圳 518102）

城市排水管網的外水診斷是當前城市排水系統提質增效項目中重點工作之一，主要包括污水管網中地下水等入滲和雨水管網混錯接診斷。污水管網中地下水等外水入流入滲會引起污水廠進廠水量增加和水質濃度下降，進廠水量超過污水廠處理量時會產生污水溢流污染，進廠水質濃度下降會降低污水廠處理效率[1]。雨水管網中混錯接會導致污水直排或溢流進入河道[2]。外水量評估是排水管網外水診斷的核心內容之一。

目前，排水管網外水量評估方法主要分為物理探測、水量平衡法、化學質量平衡法3 類，其中物理探測主要是利用潛望鏡（QV）、管道內窺檢測（CCTV）等檢測設備定位到管網外水入流入滲點[3-5]，然后進行水質水量檢測，該方法成本較高；水量平衡法[6-7]是通過對比上下游流量變化，判斷進入該段管道的外水量，該方法無法判斷外水種類和比例；化學質量平衡法則是通過上下游水質指標濃度判斷該段管道的外水類型和比例，如特征因子法[8-9]和同位素法[10]等，其檢測成本低，能評估各種外水的來水量。

特征因子法等化學質量平衡法應用的關鍵是要合理選擇特征因子。不同外水中水質指標差異較大，通常選擇氨氮、表面活性劑、安賽蜜和大腸桿菌等指標作為生活污水的特征因子，如徐祖信等[2]選擇安賽蜜來診斷上海市某雨水管網；尹海龍等[11]選擇一種微生物指示菌作為特征因子；Field 等[12]推薦氨氮、表面活性劑等作為特征因子。地下水通常選擇總硬度作為特征因子[13-14]。由于工廠生產工藝形式多樣，需結合具體情況選擇特征因子，通常電子企業的工業污水選擇氟化物作為特征因子[15-16]，食品加工企業則選擇鈉、鉀、氯化物作為特征因子[17]。

選擇不同外水的特征因子時，通常是根據某種水質指標在不同外水中的濃度具有顯著性差異來判別的，是否具有顯著性差異往往需靠經驗來判斷。本文利用統計方法給出特征因子的定量判別準則，可作為城市排水管網外水診斷時選擇特征因子的依據。

1 化學質量平衡模型

排水管網某檢查井或泵站等節點中來水滿足以下水質水量平衡方程組

式中：qi為第i 種來水的流量，i=1，2…n，n 為來水種類的數量；cij為第i 種來水的第j 種水質指標濃度，j=1，2…m，m 為水質指標的數量；Q 為該節點的總來水量；Cj為該節點中第j 種水質指標的混合濃度。將式（1）等號兩邊同時除以Q，得到以下化學質量平衡方程組

式中：xi為第i 種來水的流量占比。式（2）是一個（m，n）階非齊次線性方程組，附加一個流量平衡的約束條件，為了使方程組有唯一解，通常選擇的化學指標個數等于來水種類的個數，即m=n。當cij為隨機數時，式（2）不能通過矩陣分解、最小二乘法等線性方程組的解法進行求解，需借助蒙特卡羅等隨機方法求解[2]，求解基本步驟如圖1 所示。從節點檢測數據初步判斷上游來水的種類，從已建立的特征因子庫中挑選并隨機生成特征因子，代入式（2）中求解，循環此過程1 萬次，即可得到每種來水占比的后驗分布。

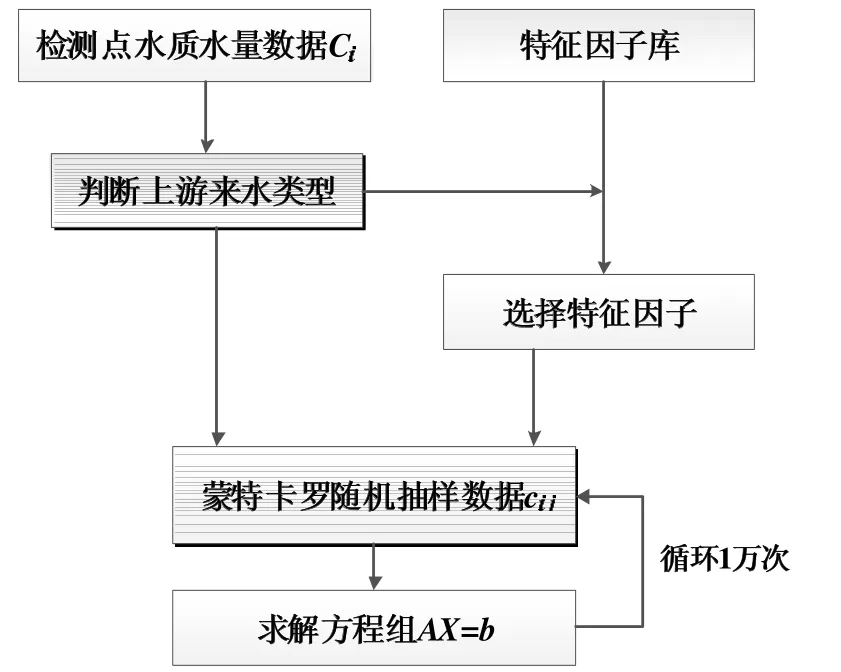
圖1 化學質量平衡方程的蒙特卡羅計算流程

2 特征因子的特性

為了保證式（2）的方程組有唯一解，選擇的水質指標需滿足以下條件[18]，方可作為特征因子：①同一種水質指標在不同外水中濃度應具有顯著性差異；②同一種外水中不同的水質指標應相互獨立，即線性無關；③水質指標濃度的變化范圍應足夠小，即較小的方差；④水質指標應具有穩定的性質，在管網中流動時不發生物理、化學變化。第④點要求是為了防止水質指標濃度從上游到下游流動過程中發生衰減。第①至③點要求本質上需要滿足方程組有唯一解。

將式（2）寫成矩陣形式

式中：A 為系數矩陣；b 為常數項向量。要保證方程（3）有唯一解，矩陣的秩需滿足以下條件

當要求①不滿足時，將矩陣A 按式（5）進行行變換，變換后矩陣A 的秩小于n，方程組有無窮解，因此特征因子必須滿足要求①。

當要求②不滿足時，將矩陣A 按式（6）進行行變換，變換后矩陣A 的秩小于n，方程組有無窮解，因此特征因子必須滿足要求②。

要求③與蒙特卡羅抽樣誤差有關，根據中心極限定理，誤差需滿足下式

式中：x 為水質指標濃度樣本均值；μ 為水質指標濃度均值；σ 為水質指標濃度樣本標準差；Zα為標準正態分布分位數；α 為置信水平。當樣本數一定時，誤差與σ 成正比，因此當水質指標濃度方差越小，計算誤差越小。

上述顯著性差異、相互獨立和較小方差的要求都是定性的，無法為特征因子的選擇提供依據，因此需要對這些要求提供具體的定量判別標準。

3 特征因子的選擇方法

特征因子顯著性差異要求可用Mann-Whitney U檢驗[19]；相互獨立要求可用Pearson 相關性檢驗[20]；較小方差要求可通過式（7）來確定標準差的置信范圍。

3.1 顯著性檢驗

Mann-Whitney U 檢驗，用來檢驗兩組數據是否服從同一分布，其計算步驟是將A、B 兩組數據混合后按升序排列，對于每個數據確定其在所屬組的序號，作為該數據的秩數，將兩組數據各自的秩數求和分別得到秩和RA和RB，然后按照式（8）計算U 值

式中：nA和nB分別為A、B 兩組數據的樣本數。通過UA和UB的最小值與預設值α 對比來進行假設推斷，如果p 小于α，則拒絕原假設H0：A、B 服從統一分布。

3.2 相關性檢驗

同一種外水中不同水質指標的相關性用以下公式計算Pearson 相關系數

式中：X、Y 為同一種外水中兩種水質指標濃度；μX和μY為X、Y 的均值；σX和σY為X、Y 的標準差。但通過相關系數來判斷的方式在實際應用時仍然是定性的，因此需引入下式的相關性顯著性指標

式中：α 為相關性顯著性標準，通常設置為0.05；n 為X、Y 的樣本數量。當相關性顯著性指標p 小于0.05時，則拒絕原假設H0：X、Y 沒有線性相關性。

3.3 標準差檢驗

式（7）中的誤差可變形為下列形式

式中：ε 為絕對誤差，其他同式（7）。將式（12）等號兩邊同時除以均值μ 得到水質指標的變異系數

式中：δ=σ/μ 為變異系數；εr為相對誤差。水質指標的變異系數與樣本數量和相對誤差的關系如圖2 所示，圖2 是雙對數坐標。當樣本為30~60 個，相對誤差控制在5%~10%時，變異系數小于0.3 的才能作為特征因子。

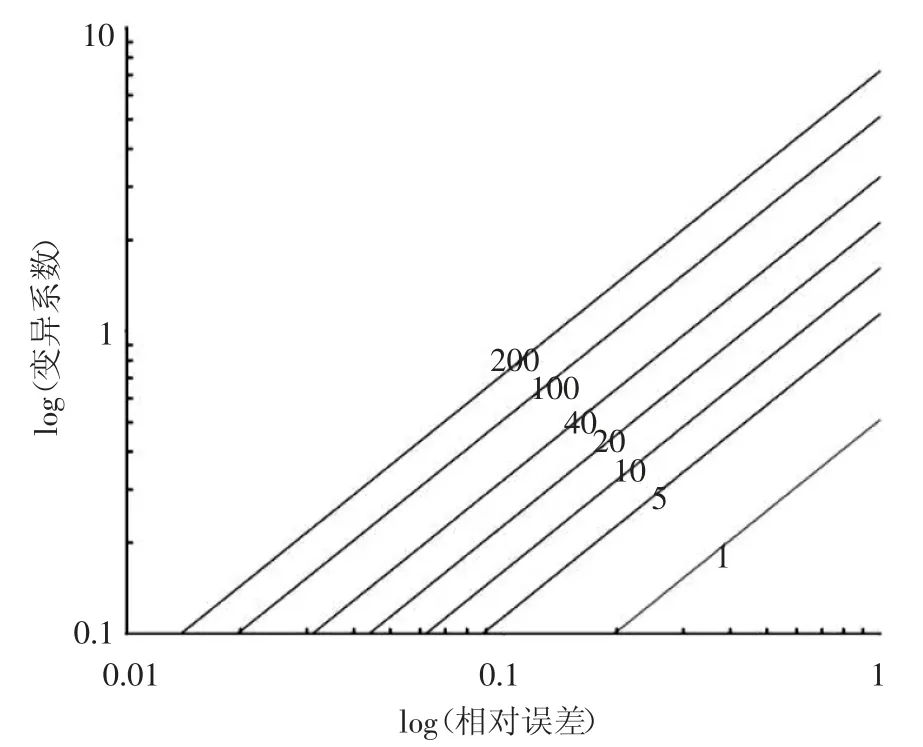
圖2 變異系數與樣本數量和相對誤差的關系

4 結論

1）分析了城市排水管網外水診斷中特征因子需滿足顯著性差異、獨立性和方差較小要求的原因，目的是保證選擇的特征因子能使化學質量平衡方程組有唯一解。

2）利用Mann-Whitney U 和Pearson 相關性檢驗等統計方法，給出了特征因子選擇流程，明確了特征因子顯著性差異和相關性判斷的定量標準。

3）闡述了水質檢測數據的變異系數、樣本數量和相對誤差之間的關系，并建議在排水管網外水診斷實際工作中，當樣本為30~60 個，相對誤差控制在5%~10%時，選擇變異系數小于0.3 的水質指標作為特征因子。