同軸送粉激光熔覆粉束質量分布密度模型與實驗測量

王軍華,許俊飛,路 妍,彭建軍,李東林,頡潭成

(1．河南科技大學 a.機電工程學院;b.材料科學與工程學院,河南 洛陽 471023;2．河南省智能制造裝備工程技術研究中心,河南 洛陽 471003;3．智能數控裝備河南省工程實驗室,河南 洛陽 471003)

0 引言

同軸送粉式激光熔覆技術是以高能量密度激光束為移動熱源,以金屬粉末為成形材料,根據預先規劃的掃描路徑逐道掃描實現金屬零件表面改性,達到強度增加和耐磨性提升的目的[1-3]。粉束內粉末顆粒的空間質量分布密度是決定激光熔覆幾何形狀尺寸的關鍵核心問題之一[4]。掌握同軸送粉粉束匯聚特性及空間質量分布是精確控制激光熔覆過程中單道沉積層截面形狀尺寸的前提。

國內外科研工作者采用數值模擬仿真、理論模型推導及實驗檢測等手段,研究送粉噴頭結構及尺寸、粉末顆粒形狀及大小、載氣流量及送粉速率等因素,對粉束運動軌跡、匯聚特性的影響。文獻[5]采用歐拉-拉格朗日框架,建立了1個四流道氣-粉噴嘴的流體動力學模型來分析送粉過程。結果表明:當內層氣體和載氣的速度相等時,由于形成了穩定的層狀粉末流,粉末流在熔池區域表現出最佳濃度。文獻[6]利用點-粒子大渦流模擬和高速成像,研究壁面粗糙度和粉末顆粒大小對從垂直圓形噴嘴發出的粉末流動特性的影響。結果顯示:壁面粗糙度增強了粉末顆粒的橫向分散性,并消除了顆粒在近壁區域的優先積累,導致了噴嘴內平均顆粒速度的降低和顆粒在噴嘴核心的聚集。文獻[7]通過基于高斯光束的射線表示法對粉末流進行建模,并通過高速相機進行實驗驗證。結果表明:在噴嘴出口位置,由高速攝像機粒子跟蹤獲得的粉末流的統計數據與該模型相符。文獻[8]為闡明粉末顆粒在連續同軸送粉過程中的傳輸機制,開發了一種試驗和匹配方法來量化,用于描述顆粒與噴嘴壁之間非彈性碰撞的恢復系數。研究發現,外層屏蔽氣體流對多層射流流場有很大影響,在外層屏蔽氣體流為20 L/min時,最有利于粉末聚焦。文獻[9]采用雷諾平均Navier-Stokes方程進行數值模擬,在不同實驗條件條件下分別進行試驗。結果顯示:仿真結果與實驗結果具有良好一致性,且氣體流速、粉末流速和噴嘴結構均對粉末流直徑有影響。文獻[10]以粉末流的焦距和有效粉斑直徑為研究對象,分析了載氣、同軸保護氣、送粉速率對粉末束流關鍵特征的影響規律,為粉末流調控提供依據。文獻[11]基于氣固兩相流原理,通過建立三維粉末流輸送模型,分析了彈性恢復系數對同軸噴嘴外流粉末場的速度場、濃度場、焦點距離和粉斑尺寸的影響。綜上可知,國內外研究人員針對側向送粉或同軸環形送粉模式,在粉束匯聚特性[12-13]、粉束內粉末顆粒空間質量分布密度[14-16]等方面做了大量研究,取得了一些成果,但研究多采用數值模擬開展,而目前應用廣泛的多粉針同軸送粉模式涉及較少。

為了實現四粉針同軸送粉模式下粉束空間質量分布密度的全參數化準確預測,本研究根據送粉噴頭結構參數和送粉工藝參數,建立粉末空間質量分布密度全參數化理論計算數學模型,并提出一種簡易的粉束內粉末顆粒空間質量分布密度實驗檢測方法,以驗證所建粉束空間質量分布密度理論模型的正確性與有效性。

1 數學模型

四粉針同軸送粉噴嘴結構模型及其粉末流示意圖,如圖1所示。在粉末輸送過程中,粉末顆粒在載

氣作用下與送粉管道及粉針內壁反復碰撞,單個粉末顆粒的運動并非沿粉針中心射出,致使整個粉束在出粉口有一定發散,在成形基面上并未匯聚一點而是一個區域。由圖1可知:不同粉針噴射粉束在與出粉口垂直距離fb處匯聚為一點,此時,fb為焦距,θ為粉束發散角,α為粉針與成形基面夾角。

1.1 單粉針粉束質量分布密度數學模型

在建立單粉針粉束質量分布密度數學模型前,需作出基本假設[17-18]：若要建立單粉針粉束在空間任意平面內粉末質量分布密度數學計算模型,則應將其在垂直粉管軸線上相應平面內的高斯分布函數進行幾何關系轉化。空間任意平面內單粉針粉束質量分布密度幾何關系轉化示意圖如圖2所示。

通過引入離焦量的影響,以(fb+DL)作為限定目標平面位置變量,表示目標平面至粉針出粉口的垂直距離。單粉針粉束在垂直于粉針中心軸線X0O0Y0平面內服從高斯分布,在該平面內其粉末質量分布密度可表示為:

(1)

其中:r0為X0O0Y0平面內粉束半徑,mm,其大小隨垂直于粉針中心軸線平面位置的改變而變化。同時,若要根據X0O0Y0平面內粉束質量分布密度,通過理論計算獲得X1O1Y1平面內粉束質量分布密度,需對圖2中各參數之間的關系進行幾何換算,各參數間關系可由公式(2)表示:

r0=r′+Ltanθ;

(2)

(3)

(4)

(5)

其中:r′為單粉針出粉口半徑, mm;L為X0O0Y0平面沿粉針中心軸線方向至出粉口距離,mm;fb為粉斑焦距,mm;DL為離焦量,mm;α為單粉針與成形基面夾角,其取值應視具體送粉噴頭結構而定,本研究所用送粉噴頭α為65°;D為粉針出粉口間距,mm, 本研究所用送粉噴頭D為15.6 mm。

針對單粉針噴射粉束,當送粉工藝參數一定時,送粉過程是穩定的,可以認為粉束空間內某點處粉末質量分布密度恒定不變。而該點處粉末質量分布密度函數表達與所考察目標平面有關,有:

f1(x1,y1)Δx1Δy1=f0(x0,y0)Δx0Δy0。

(6)

由公式(4)和公式(6)可知,空間任意平面內某一點P處粉末質量分布密度函數可表示為:

(7)

1.2 四粉針粉束質量分布密度數學模型

四粉針同軸送粉模式粉束在空間任意平面內粉末質量分布密度坐標轉換示意圖如圖3所示。由圖3可知,由于四粉針同軸送粉噴嘴空間結構的對稱性以及送粉參數一致性,各粉針噴射粉束在目標平面內的形狀尺寸完全相同,只是方向和位置存在一定差異。在XOY平面內通過沿坐標原點O旋轉,則可以實現彼此完全重疊。通過對4個不同粉針噴射粉束在XOY平面內的粉斑建立如圖3所示坐標系,則可通過公式(7)計算不同粉束在各自坐標系內的粉末質量分布密度,然后利用坐標轉換公式(8),可將其轉化為XOY平面內的粉末質量分布密度函數。

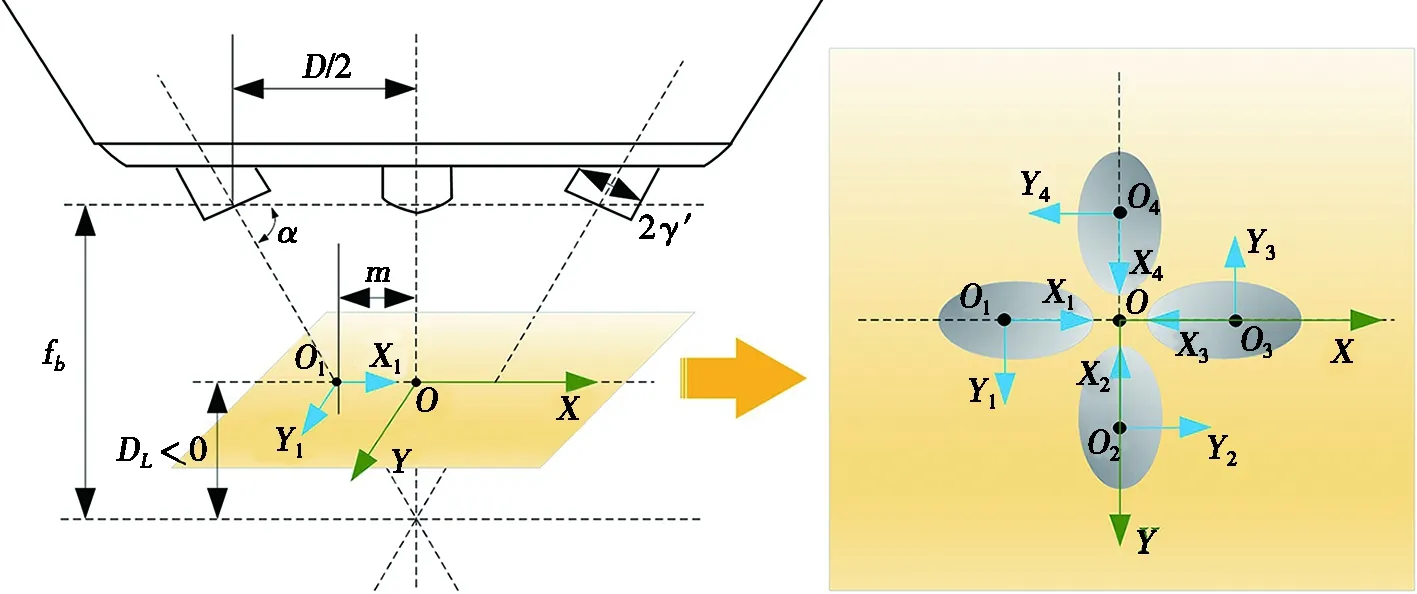
圖3 四粉針同軸送粉噴嘴粉束在空間任意平面內粉束坐標轉換示意圖

坐標系轉換關系可以表示為:

(8)

由于公式(1)是經過歸一化處理后的粉末質量分布密度模型,由此推導出的公式(7)也是歸一化模型。為了實現真實送粉工藝參數條件下,四粉針同軸送粉模式下粉束粉末質量分布密度預測計算,需要引入送粉速率,并將其送粉量均勻分散在四粉針內,同時結合坐標轉換公式(8),可將空間任意平面內某一點P處的粉末質量分布密度函數表示為:

(9)

另外,發散角θ可由公式(10)給出[19]：

(10)

其中:ν為載氣運動黏度,mm2·s-1;V0為載氣流速,mm·s-1,可以表示為:

(11)

其中:Lp為載氣流量,L·min-1;rpipe為輸粉管內徑,mm。

對于具體送粉噴頭而言,結構尺寸固定,相應參數均為常數,比如粉針軸線傾角、出粉口半徑、粉針出粉口間距等。因此,針對四粉針同軸送粉模式來說,真正影響粉束內粉末顆粒空間質量分布密度的只有送粉速率和離焦量。

1.3 同軸送粉模式粉束質量分布密度Matlab計算

不同離焦量四粉針同軸送粉模式下,粉束在空間任意平面內匯聚情況示意圖如圖4所示。由圖4可知:當目標平面位于焦平面上方時,其離焦量為負值,此時單個粉針噴射粉束未到達焦點位置,各自靠近出粉口位置,各粉束未完全匯聚,激光束輻照O點處粉末質量分布密度較小,當離焦距離較大時,O點處粉末質量分布密度甚至為0;同樣,當目標平面位于焦平面下方時,其離焦量為正值,此時單個粉針噴射粉束越過焦點位置,使得各粉束無法完全匯聚,激光束輻照O點處粉末質量分布密度也有所降低,不同的是此時總有粉末顆粒被激光束輻照。

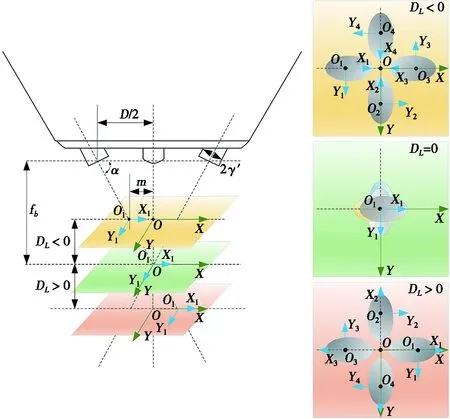
圖4 不同離焦量條件下四粉針同軸送粉模式下粉束匯聚情況示意圖

為了研究不同離焦量條件下目標平面內粉束質量分布密度特征,利用Matlab軟件對公式(9)進行計算,進而定量計算了不同成形基面上粉束質量分布密度函數fp(x,y),計算所用各參數如表1和表2所示。

表1 理論計算所用送粉工藝參數

表2 理論計算所用送粉噴嘴結構參數

不同離焦量條件下,目標平面內粉束質量分布密度理論計算結果如圖5所示,XY平面為考察目標平面,該考察目標平面內不同位置處粉末質量分布密度如縱坐標所示。如圖5a所示,當考察目標平面在焦平面上方且離焦量較大時,四粉針同軸送粉噴嘴噴射粉束在此平面內并未匯聚,各粉束噴射粉末顆粒在XY平面O點位置(激光束輻照位置)只有極少一部分,致使此處粉束質量分布密度相對較小,相應地在激光熔覆時粉末利用率較低。由圖5b可知:當考察目標平面在焦平面附近時,四粉針同軸送粉噴嘴噴射粉束匯聚特性較好,在XY平面O點位置(激光束輻照位置)粉末質量分布密度相對較大,分布特性近似高斯分布特征。尤其是在離焦量為0的焦平面上,粉束匯聚特性最好,粉束質量分布密度呈現高斯分布特征,即在激光輻照位置粉末質量分布密度達到最大值,相應地在激光熔覆過程中粉末利用率也將最大。由圖5c和圖5d可知:當考察目標平面在焦平面下方且離焦量較大時,在XY平面O點位置(激光束輻照位置)粉末質量分布密度顯著下降,同時粉束匯聚特性變差,粉斑尺寸明顯增大。由此可知,當考察目標平面偏離焦平面時,無論離焦量為正還是負,隨著離焦量絕對值的增大,考察目標平面上粉斑尺寸逐漸增大,激光束輻照位置處粉末質量分布密度逐漸減小[124]。

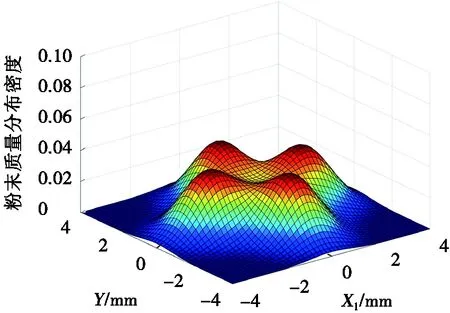
(a) DL=-3.5 mm

由于四粉針同軸送粉噴嘴結構的對稱性,粉束質量分布密度曲線在X軸和Y軸線完全相同。不同離焦量條件下X軸線截面內粉末質量分布密度如圖6所示。從圖6中明顯看出:當離焦量不同時,X軸線截面內粉末質量分布密度差異顯著。當離焦量為0 mm時,粉末質量分布密度曲線呈現高斯分布特征,激光輻照區域內粉末質量分布密度最大;當離焦量在±1.5 mm范圍內時,X軸線截面內粉末質量分布密度基本服從高斯分布,粉束匯聚特性相對較好。隨著離焦量的增大,無論是正離焦還是負離焦,粉束匯聚特性顯著變差,激光輻照區域內粉末質量分布密度顯著降低。

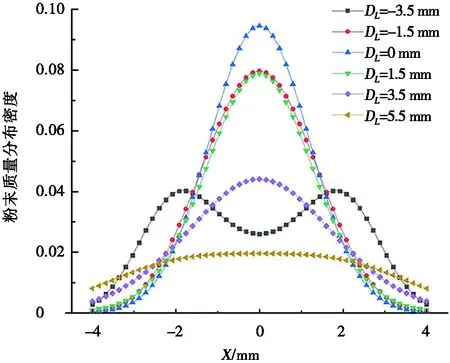
圖6 不同離焦量條件下X軸截面內粉末質量分布密度對比

2 實驗研究

2.1 粉束質量分布密度測量方法

粉束內粉末質量分布密度的準確測量十分困難,原因就在于送粉過程為動態過程,且不同水平面內粉束形狀及質量分布密度均存在差異[20]。若要實現空間任意平面內任一位置處粉末質量分布密度的準確測量,核心問題則是目標平面內待考察位置處粉末顆粒的高精度收集與測量。為了解決這一問題,提出利用內徑為0.5 mm的銅管作為集粉管,在單位時間內較為精確地收集粉束內待考察位置粉末顆粒并稱質量,然后計算出該位置的粉末質量分布密度。如果單位時間內,運動到粉束內某位置處(單位面積)的粉末顆粒質量已知,此時粉末顆粒質量則為該位置處的粉末質量分布密度,由此則有:

(12)

其中:fc(x,y)為目標平面待考察位置處粉末質量分布密度,g·mm-2·min-1;mc為集粉器內粉末顆粒質量,g;rc為測量銅管內徑,mm;tc為測量用時,min。

粉末質量分布密度實驗測量方法示意圖如圖7所示。由圖7可知:將內徑為0.5 mm的銅管放置于粉束區域目標平面待考察位置處,確保集粉銅管頂部端面與目標平面重合。在預設送粉參數條件下打開送粉裝置,粉束內待考察位置處粉末顆粒將射入集粉銅管管口區域內,并沿集粉銅管內壁自由下落進入集粉器,以2 min為計時單位,利用電子天平稱量集粉器內收集的粉末質量,然后利用公式(12)計算出粉末質量分布密度。通過不斷變換目標平面待考察點的位置,重復上述操作,則可實現目標平面不同位置處粉末質量分布密度測量。

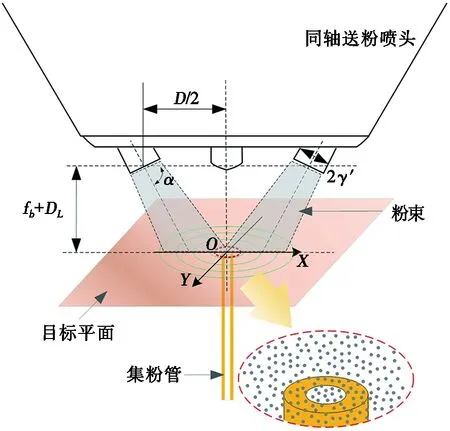
圖7 粉束質量分布密度實驗測量方法示意圖

2.2 粉束質量分布密度測量裝置及參數選擇

實驗所用粉材為17-4PH,粉末形貌及粒度分布分別如圖8和圖9所示,粉末密度為7.9 g·cm-3。實驗參數如表3所示。實驗所用粉材為馬氏體沉淀硬化不銹鋼(17-4PH)粉,粉末顆粒呈圓球形,粒度為50～110 μm。由圖8和圖9可知:實驗所用馬氏體沉淀硬化不銹鋼(17-4PH)粉材粒度均勻,粒度主要為80～90 μm。

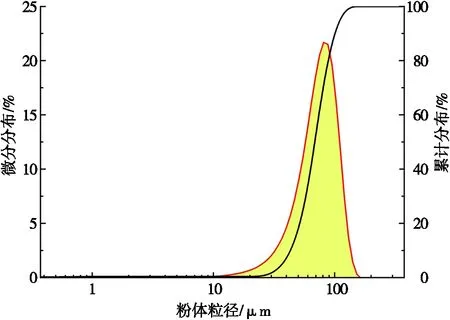
圖9 馬氏體沉淀硬化不銹鋼(17-4PH)粉末顆粒粒度分布 (120倍)

表3 實驗所用參數

實驗檢測過程是將內徑為0.5 mm的集粉銅管連同集粉器一起固定在機床工作臺上,通過調整數控機床工作臺,確保集粉銅管頂部端面與目標平面重合,并放于粉束區域目標平面待考察位置處。然后,在預設送粉參數條件下打開送粉裝置,以2 min為計時單位,計時結束后利用電子天平稱量集粉器內收集的粉末質量。此后,通過控制數控機床工作臺將集粉管移動至下一測量點,重復上述操作。在每個目標平面內,測量點如圖10所示,分別沿如圖10所示XY軸每隔1 mm測量1個位置點,每個目標平面內共測17個位置點。

為了考察不同離焦量條件下粉末質量分布密度變化情況,通過三軸聯動數控裝置控制激光噴頭沿Z軸移動,調整其與集粉銅管頂部端面間的距離,實現離焦量的調整。本實驗研究共檢測3個目標平面,其離焦量分別為 -3.5 mm、-1.5 mm、0 mm、5.5 mm,每個目標平面內共檢測17個考察位置點,每個位置點重復測量3次求取平均值,然后分別代入公式(12),計算相應考察位置處粉末質量分布密度。

3 分析討論

不同目標平面內X軸不同位置處粉末質量分布密度實驗測量結果如圖11所示。由圖11可知:不同目標平面內,粉束內粉末質量分布密度差異顯著。不同目標平面以及同一目標平面的不同位置處,粉末顆粒質量分布密度存在顯著差異。如圖11c所示,當目標平面離焦量為 0 mm時,粉束內在X軸截面內粉末質量分布密度呈現近似高斯分布特征,相比其他目標平面而言,此時在激光輻照O點位置粉末質量分布密度最大,而且粉束尺寸最小,匯聚特性最好。當目標平面離開焦平面,即有一定離焦量時,無論離焦量為正還是為負,激光輻照位置(X軸原點O)粉末質量分布密度均出現不同程度下降,且偏離焦平面距離越遠,粉末質量分布密度下降越顯著。與正離焦不同的是,當目標平面離焦量為-3.5 mm時,粉束內在X軸截面內粉末質量分布密度不再服從高斯分布,而是呈現雙駝峰分布特征,如圖11a所示,這說明此目標平面內多粉口噴射出粉末流并未匯聚一處。

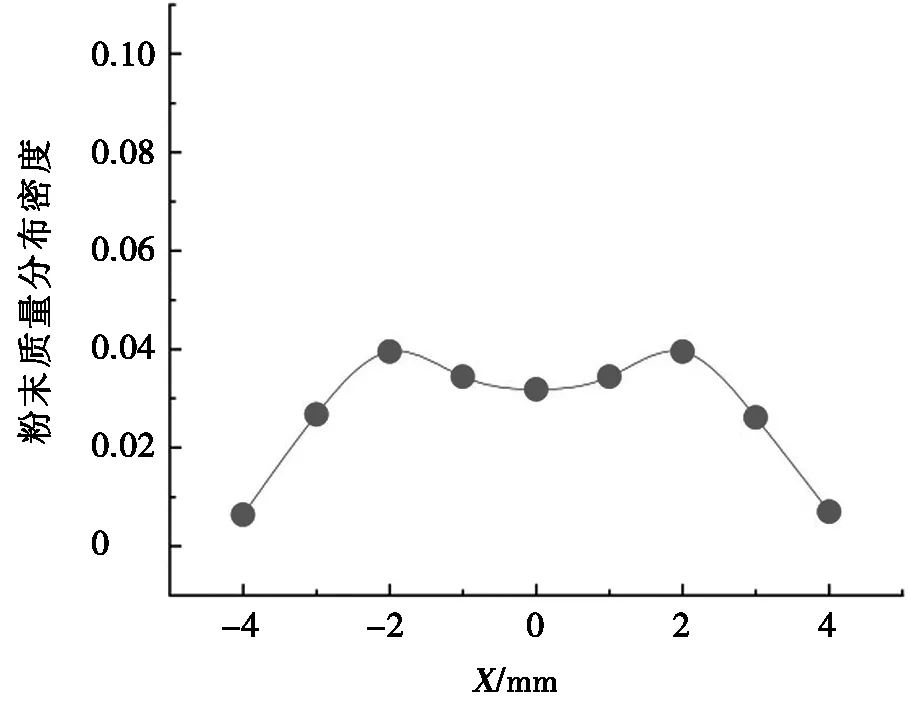
(a) DL=-3.5 mm

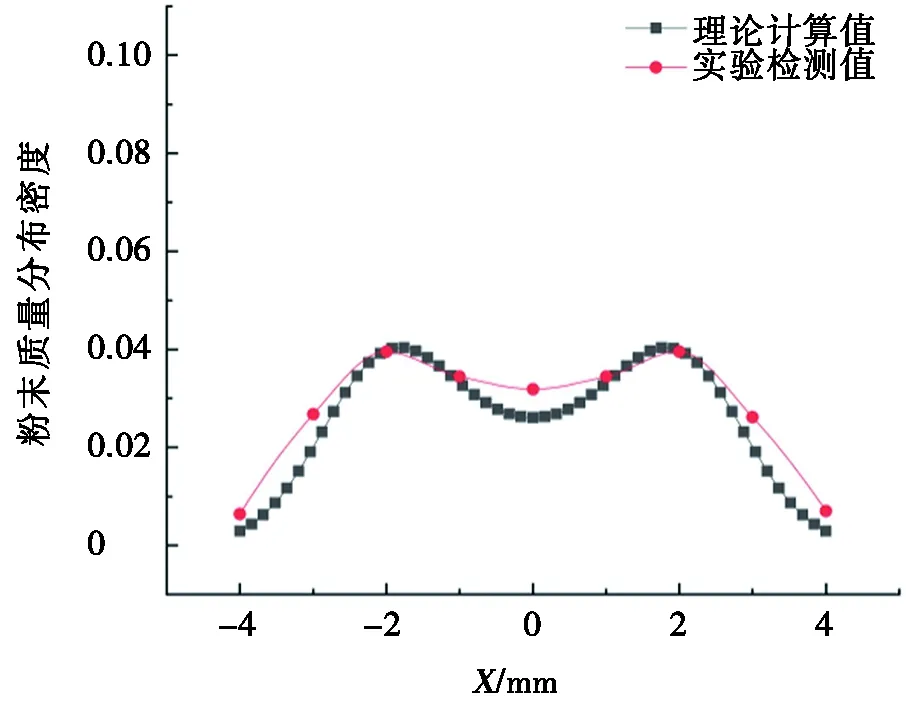
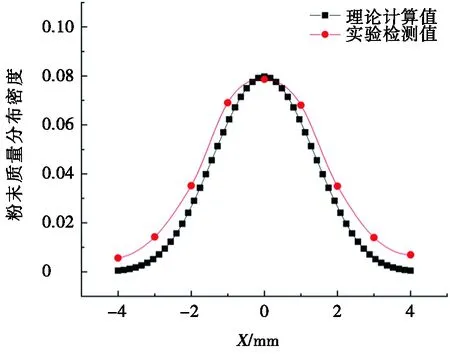
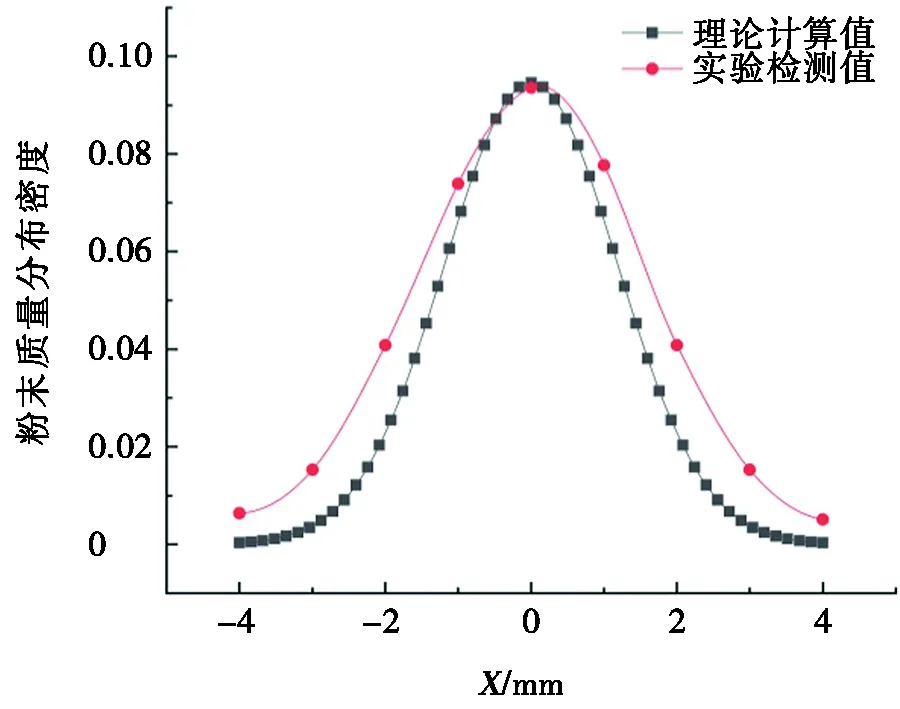
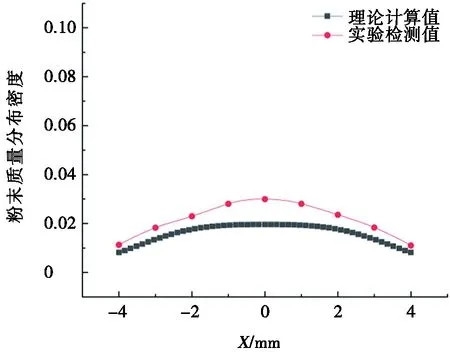
結合不同目標平面內X軸不同位置處粉末質量分布密度實驗測量結果,將其與理論計算結果進行對比分析,進一步驗證前文所建立的粉末質量分布密度理論計算模型的正確性。不同目標平面內X軸不同位置處粉末質量分布密度理論計算與實驗檢測結果對比如圖12所示。由圖12可知:不同目標平面內X軸不同位置處粉末質量分布密度理論計算與實驗檢測結果吻合較好,不同目標平面內粉末質量分布密度理論計算結果和實驗檢測結果變化趨勢完全相同,尤其是目標平面接近焦平面時(離焦量較小情況),在激光輻照位置處二者高度吻合,接近100%(如圖12b和圖12c所示),說明前文所建立理論計算模型可以用于四粉針同軸送粉模式下粉束內粉末質量分布密度的準確計算。

然而,理論計算與實驗檢測結果之間也存在一定偏差,如圖12d所示O點附近和圖12b～圖12cO點兩側2～4 mm處,偏差相對較大。分析認為,造成理論計算和實驗檢測結果出現誤差的原因可能是實際送粉過程中單粉針噴射粉束發散角大于理論計算值(如圖13所示),由于建立粉束質量分布密度理論模型時假定單粉束粉末顆粒運動至發散角以外的可能性為0,而實際送粉時極有可能出現部分粉末顆粒射出理論發散角以外,即實際發散角大于理論發散角,此時運動至A區域粉末顆粒增多,導致圖12a中激光輻照區域粉末顆粒增大,相應粉末質量分布密度大于理論計算值。同理,由于實際發散角偏大,運動至B區域內的粉末顆粒也增多,導致實驗檢測時圖12b～圖12c中激光輻照區域兩側2～4 mm處粉末質量分布密度大于理論計算值。而在如圖13所示C區域內,粉末質量分布密度增大的原因可能是不同粉針噴射出粉束在聚焦點處匯聚,粉末顆粒相互之間的碰撞或者在其他粉束載氣作用下,粉末顆粒水平運動速度降低,致使粉束內多數粉末顆粒下落在C區域,導致此處實驗測量數值高于理論計算數值,這或許就是圖12d所示粉末顆粒質量分布密度實際測量值大于理論計算值的原因所在。

(a) DL=-3.5 mm

(b) DL=0 mm

(c) DL=3.5 mm

(d) DL=5.5 mm

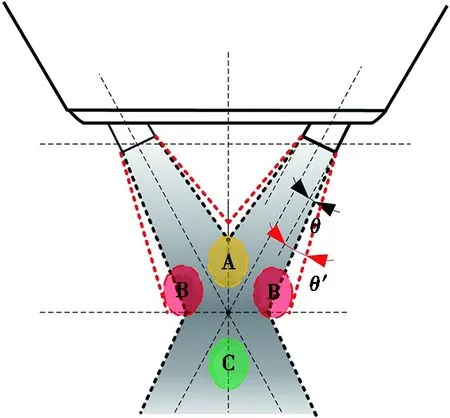
圖13 粉束發散角對粉末質量分布密度影響分析示意圖

4 結論

(1)空間任意平面內粉束質量分布密度主要取決于送粉速率、離焦量和送粉噴頭結構尺寸等參數;對具體送粉噴頭而言,結構尺寸固定,而真正影響粉末質量分布密度的因素,則是送粉速率和離焦量;

(2)不同目標平面內,粉束內粉末質量分布密度差異顯著。當目標平面有一定離焦量時,無論正離焦量還是負離焦,光斑處粉末質量分布密度均下降,且離焦量越大下降越顯著。