6G 密集網絡中基于深度強化學習的資源分配策略

楊凡，楊成，黃杰，張仕龍，喻濤，左迅，楊川

（重慶理工大學電氣與電子工程學院，重慶 400054）

0 引言

6G 密集網絡（DN,dense network）是一個面向智慧醫療、全息通信、智慧城市群、應急通信搶險、智能工廠以及數字孿生等全場景的網絡，可實現通信和人工智能（AI,artificial intelligence）的雙向互促[1]。隨著智能終端（IT,intelligent terminal）的空前普及和網絡規模的快速擴展，5G DN 無法完全滿足不斷上升的技術標準，如自主、超大規模、高度動態和完全智能的服務。未來智能化和智能物聯網網絡的快速增長可能超過5G DN 的能力。與5G DN 相比，6G DN將支持10 倍高的網絡容量和十分之一的時延，同時服務10倍多的終端設備數量以及提高服務質量（QoS,quality of service）[2-3]。6G DN 將主要由AI 驅動，AI 技術可實現從“物聯”到“智聯”的躍遷，徹底改變無線網絡[4]。對于6G DN 而言，優化資源分配是保證網絡性能的基本機制。通過基于AI 的智能資源分配和復用，可以緩解海量連接對資源的巨大需求，從而顯著提高資源復用率[5]。另一方面，大數據促進了AI 在資源管理中的應用，AI 可通過挖掘數據來學習各種模式（如用戶流量模式和移動模式）或復雜的相互關系。6G DN 的主要優點是鏈路強度的提高和廣泛的頻譜復用。但IT 節點的密集分布導致小區間交疊干擾加劇，網絡容量下降，同時交疊干擾造成了網絡吞吐量與IT 節點數量不成線性關系[6]，使6G DN 的資源利用效率和服務質量急劇降低。因此，在密集網絡下如何進行資源分配使密集網絡的小區間無交疊干擾是提升6G DN 性能亟待解決的問題[2]。

目前，優化方法已經用于解決密集性無線網絡的資源分配問題[7-13]。例如，考慮密集且復雜的網絡中端到端（D2D）用戶共享相同資源產生的同頻干擾，文獻[7]基于外部性匹配理論提出一種干擾感知資源分配算法，通過最小化同頻干擾來最大化網絡吞吐量。考慮D2D 通信會引入額外干擾破壞蜂窩網絡連續干擾消除的解碼條件，文獻[8]研究聯合D2D 模式選擇和資源分配的組合優化（CO,combinatorial optimization）問題，提出一種聯合資源分配和模式選擇方法。針對密集部署IT 帶來的嚴重小區干擾，文獻[9]基于回歸方法對干擾建模，提出一種面向干擾的資源分配框架。但是，在6G DN 資源分配過程中還需考慮功率控制對干擾的影響。為保證用戶的QoS，文獻[10]研究多目標的資源分配優化問題，考慮每個用戶的傳輸功率和QoS 約束，提出一種面向功率控制的資源分配算法。文獻[11]研究聯合資源分配和功率分配的優化問題，考慮D2D 間和小區間干擾的統計信息，提出基于多項式時間算法的資源分配策略。文獻[12]研究支持非正交多址的聯合資源分配問題，考慮功率控制、最小速率和連續干擾消除的約束，采用 KKT（Karush-Kuhn-Tucker）條件和對偶理論提出一種用于資源分配的梯度迭代算法。此外，考慮到6G DN中存在的交疊區域會造成信道間較嚴重的功率干擾，文獻[13]研究密集網絡的能源效率問題，提出一種基于能量感應架構的干擾感知資源分配方法。此外，為適應6G DN 中多用戶、多小區、多頻段的無線通信場景，資源分配過程中還需考慮用戶需求差異和區分干擾類型[14-15]。針對異構網絡的同層干擾和用戶需求的多樣性，文獻[14]研究聯合次頻帶和資源塊分配優化問題，考慮用戶QoS 要求和功率限制，提出一種基于干擾管理的聯合資源分配。文獻[15]研究聯合資源分配和用戶選擇問題，考慮干擾拓撲的復雜性和資源的有限性等約束，提出一種分布式自優化資源分配方法。然而，使小區間無交疊干擾的資源分配是非凸且NP-hard 的CO 問題，難以求解[16]。此外，上述方法難以適應大規模數據的實時計算，無法充分挖掘隱藏在海量數據中有價值的信息，不能識別網絡中的通信資源復用情況，這將造成網絡吞吐量和用戶QoS 下降。因此，基于優化方法的資源分配策略難以滿足6G DN 在不同業務對資源的需求，對有限的網絡資源利用不夠充分。

深度強化學習（DRL,deep reinforcement learning）作為數據、算法和算力復合驅動的機器學習技術已廣泛應用于醫療、金融和交通等領域[17]。DRL 通過挖掘數據來學習復雜的相互關系，依靠豐富的計算能力實現實時在線決策，可彌補以犧牲存儲空間來提高系統性能的缺點，解決沒有初步離線計算結果情況下無法及時處理任務的問題。此外，DRL 可有效應對非凸和NP-hard 挑戰，解決優化方法難以求解的CO 問題[18]。然而，利用DRL 實現小區間無交疊干擾，提高網絡吞吐量和資源復用率的資源分配方法較少且研究更多關注的是非密集網絡或低密集網絡的資源分配[19-20]。考慮到6G DN中資源分配本質問題為CO 問題，DRL 能有效解決在滿足網絡吞吐量、資源復用率以及無交疊干擾約束下的資源分配問題，本文提出一種基于DRL 的資源分配方法，利用深度Q 網絡（DQN,deep Q-network）模型和競爭網絡結構對6G DN 進行通信鏈路的資源分配以及實現小區間無交疊干擾，以提高網絡吞吐量和資源復用率。本文主要貢獻如下。

1) 針對密集交疊干擾下的6G DN 場景，構建6G DN 覆蓋模型，提出以最小化密集交疊干擾為優化目標的CO 問題，為分析密集網絡場景下網絡拓撲對交疊干擾的影響提供數學依據和評估指標。

2) 提出基于點線圖染色的交疊干擾模型和實現無交疊干擾的資源分配策略。首先根據歐氏距離和無交疊干擾準則，建立6G DN 的交疊干擾模型，為計算資源分配導致的交疊干擾提供理論依據。然后，根據交疊干擾模型設計了避免交疊干擾的資源分配策略，解決6G DN 中交疊干擾問題。

3) 為實現6G DN 中網絡無交疊干擾的資源分配，構建基于DQN 的資源分配模型，提出基于Dueling DQN 的資源分配算法，采用競爭網絡結構感知交疊干擾特征，通過馬爾可夫決策過程（MDP,Markov decision process）優化網絡資源分配的過程，實現無交疊干擾的密集組網，為求解非凸和NP-hard 的資源分配問題提供一種新的求解方法。

最后本文對所提方法進行仿真實驗和實際通信測試。結果表明，基于Dueling DQN 的資源分配算法可根據6G DN 的網絡拓撲得到資源分配方案，避免交疊干擾，有效地提高網絡吞吐量和資源復用率。

1 系統模型

本文考慮如圖1 所示的復雜通信場景中的6G DN 模型，該6G DN 由N個IT 組成，IT 之間形成M條通信鏈路。其中IT 的覆蓋范圍約為250 m[21]，主要用于較短距離間的通信。為進一步提高整個網絡覆蓋區域內的網絡吞吐量，在6G DN 中采用密集部署IT 的方式。當大量IT 密集部署在6G DN 中時，6G DN 將產生密集交疊干擾和資源復用沖突，從而使6G DN 的資源分配能力下降。

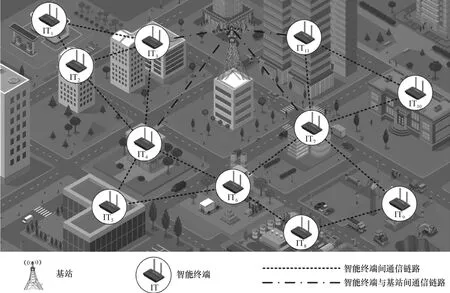
圖1 復雜通信場景中的6G DN 模型示意

6G DN 的網絡覆蓋模型通過IT 間的歐氏距離建立。本文通過無向圖模型將資源分配問題轉化為圖的邊染色問題，利用點線圖染色理論建立交疊干擾模型。

1.1 網絡覆蓋模型和6G DN 的網絡拓撲

1) IT 通信覆蓋與通信鏈路形成

圖1 中，6G DN 通信節點主要是IT，并且IT間可以通過D2D 進行通信。圖2 是圖1 中IT1、IT2和IT3形成的自組網，任意一個IT 都在其余IT 的無線覆蓋范圍之內。IT1、IT2和IT3間都存在數據傳輸的通信鏈路。IT 間的通信鏈路形成可表示為

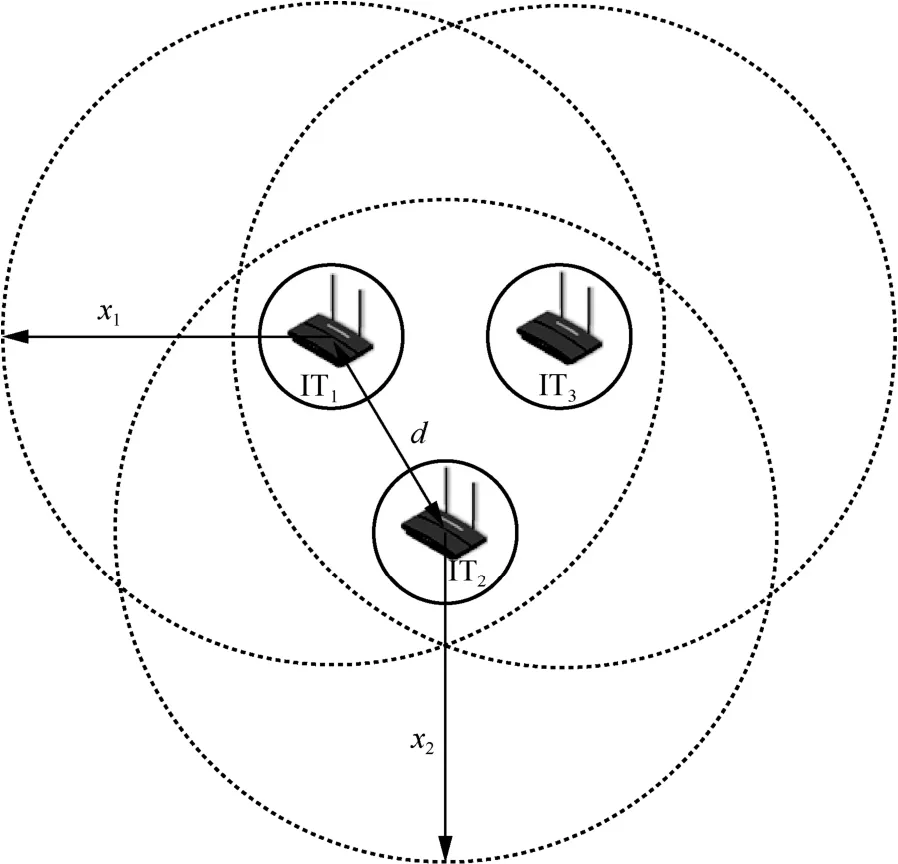
圖2 IT 通信覆蓋與通信鏈路形成

其中，d1,2表示IT1和IT2之間的歐氏距離；x1和x2分別表示IT1和IT2的通信半徑。實際情況中IT 間存在差異，因此x1≠x2。

2) 6G DN 覆蓋模型

圖3 是圖1 根據IT 覆蓋范圍得到的6G DN 覆蓋范圍模型，其中任意2 個IT 可以通信。6G DN通信覆蓋范圍CG是所有IT 通信覆蓋范圍的疊加，可表示為

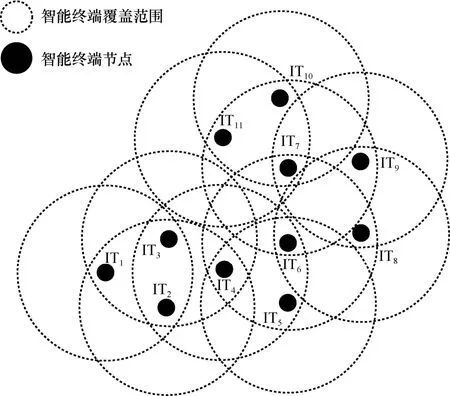
圖3 6G DN 覆蓋范圍模型

其中，Ci表示ITi的通信覆蓋范圍，T表示所有IT的集合。

3) 6G DN 的網絡拓撲

圖4 是圖3 根據式(1)得到的6G DN 的網絡拓撲。其中，網絡拓撲中的節點表示具有通信能力的IT，拓撲中的線表示節點間的通信鏈路。6G DN 點線圖模型可表示為

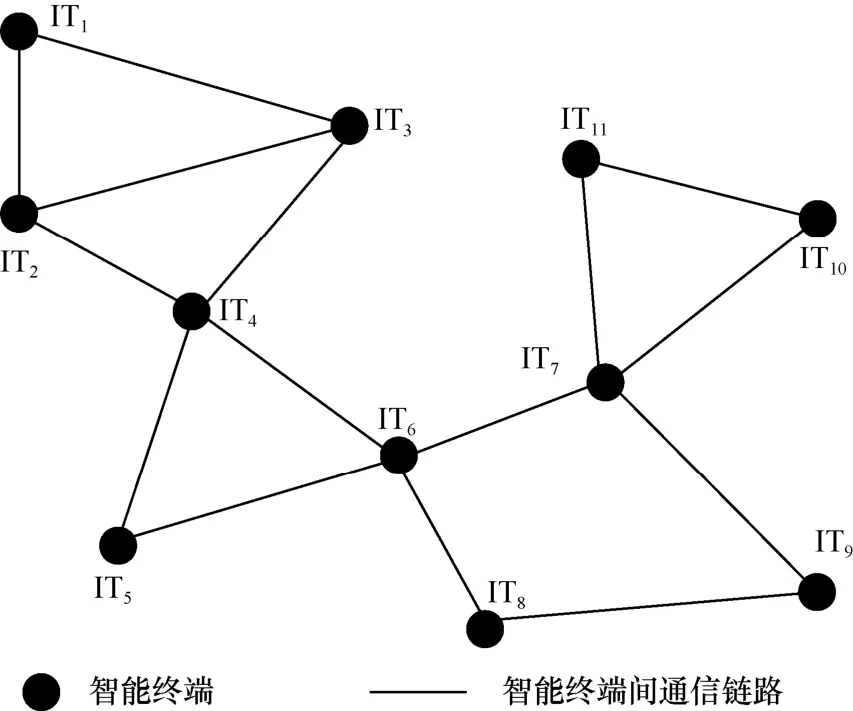
圖4 6G DN 的網絡拓撲

其中，V={1,2,…,N}表示6G DN 中的IT 集合，E={1,2,…,M}表示6G DN 中的通信鏈路集合。

1.2 6G DN 的資源分配問題

本節根據點線圖邊染色與6G DN 的網絡拓撲對應，對6G DN 中的每一條通信鏈路分配通信資源。若圖4 中相同節點的通信鏈路具有不同的通信資源，則6G DN 資源分配可表示為

其中，ψ(e,e′) 表示通信鏈路e和通信鏈路e′的關系，且ψ(e,e′) 只有2 個取值，ψ(e,e′)=1表示通信鏈路e和通信鏈路e′具有相同的通信資源，否則ψ(e,e′)=0；le∩le′=?表示通信鏈路e和通信鏈路e′在圖4 中不存在公共的通信節點。

2 6G DN 交疊干擾模型

本節提出一種使網絡無交疊干擾的資源分配策略，建立6G DN 的交疊干擾模型，降低在密集網絡交疊干擾下的資源分配難度，實現無交疊干擾資源分配。在建立無向圖網絡模型后，利用關聯矩陣設計資源分配策略。

2.1 基于點線圖染色的交疊干擾模型

其中，行向量le中的元素表示通信鏈路e與對應IT的關系，元素為1 則表示IT 利用該通信鏈路e進行通信。由于通信鏈路e能且僅能被2 個IT 使用，可表示為

根據圖5 得到對應的關聯矩陣HG為

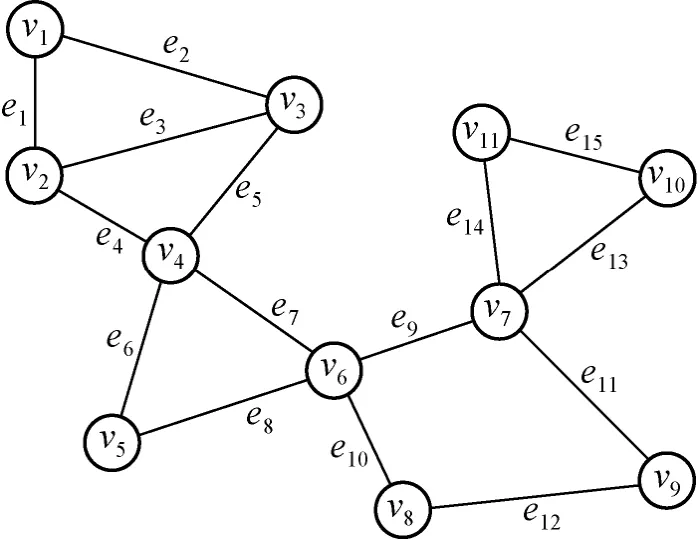
圖5 6G DN 的無向圖模型

當6G DN 對通信鏈路進行資源分配時，6G DN需要考慮密集網絡帶來的密集交疊干擾問題。交疊干擾由單個IT 使用單個通信資源和多個IT 進行通信導致。因此，單個IT 受到的交疊干擾可表示為

其中，M表示6G DN 通信鏈路的總數。式(10)表示通過對每個節點求和再進行平均可得到整個6G DN 的交疊干擾程度。

通信鏈路資源分配情況如圖6 所示。根據式(9)可知，IT6受到的交疊干擾計算過程可表示為

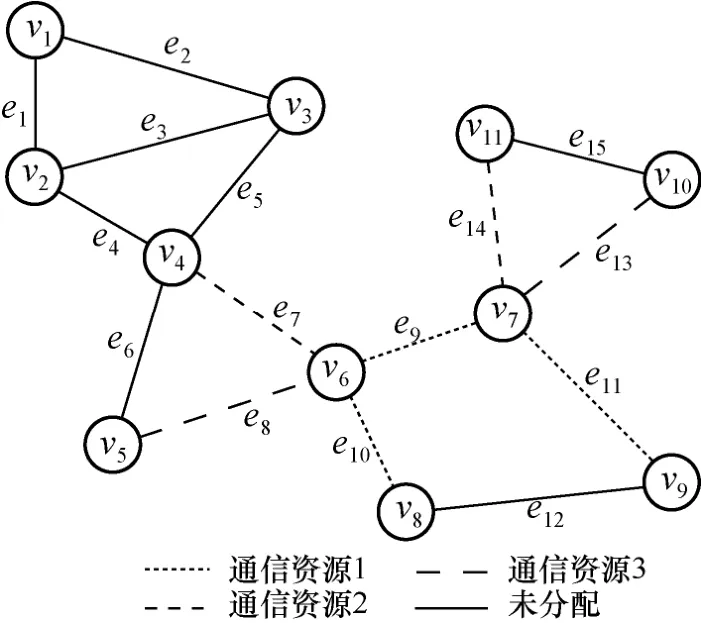
圖6 通信鏈路資源分配情況

2.2 基于交疊干擾模型的資源分配策略

在所有IT 組成6G DN 的過程中，根據式(10)可求得6G DN 資源分配導致的交疊干擾程度。因此，δG=0表示6G DN 資源分配無沖突。資源無沖突分配策略是從起始狀態到最終狀態的過程中，保證6G DN 無交疊干擾的資源分配方法。6G DN 狀態st+1的資源分配只與狀態st的資源分配結果有關，即6G DN 的通信鏈路資源分配具有馬爾可夫性質。本文提出使用有限長馬爾可夫鏈解決無向圖染色問題，建立任意時間t滿足δG=0條件的狀態轉移矩陣P。6G DN 從初始狀態s0到最終狀態s*的狀態轉移矩陣P可表示為

然而，6G DN 無法直接從通信環境中獲得狀態轉移矩陣P。因此，6G DN 需要依次對通信鏈路進行資源分配，從而使狀態st改變為狀態st+1。6G DN的資源分配動作可表示為

其中，s表示6G DN 的狀態，包含網絡拓撲情況和通信鏈路的資源分配情況；a表示通信鏈路分配通信資源；資源分配策略π表示在狀態s做出資源分配動作a的概率，具體可表示為

根據式(14)和式(15)，6G DN 在狀態s下進行資源分配后，轉移到狀態s′的概率可表示為

當6G DN 執行資源分配動作a使δG=0時，狀態s轉移到狀態s′ 的概率為p(s′|s,ai)=1。如果δG≠ 0，則表示狀態s無法轉移到狀 態s′，即p(s′|s,ai)=0。因此，根據系統狀態轉移矩陣P得到系統求解最優資源分配問題，即得到最優資源分配策略π*。其中，資源分配策略π會產生具體的資源分配方案τ，并且根據不同網絡狀態產生的分配方案τ也不同。資源分配策略π產生資源分配方案τ的概率可表示為

其中，ρ0（S0）表示6G DN 起始網絡狀態分布。式(17)可有效地表示每個分配方案τ與策略π之間的關系。考慮動態情況，網絡拓撲或者結構發生變化將會直接影響馬爾可夫鏈的狀態值。因此，在6G DN的動態情況下，6G DN 的資源分配過程可表示為

3 基于深度強化學習的資源分配策略

為求解6G DN 無干擾資源分配策略問題，本文提出基于Dueling DQN 的資源無沖突分配DRL 算法，構建6G DN 交疊干擾下的資源分配MDP 模型，結合競爭網絡模型求解最優資源分配策略π*。在6G DN 中，MDP 通常由動作A、狀態S、即時獎勵R和動作價值函數Q(s,a)組成，接下來對其進行詳細的介紹。

3.1 基于深度Q 網絡的資源分配模型

本文算法引入DQN 方法來確定6G DN 場景下資源無沖突分配的決策序列，并進行網絡拓撲信息和資源分配情況提取，利用即時獎勵函數Rt設計交疊干擾判斷機制，通過即時獎勵函數Rt判斷6G DN交疊干擾的狀態和資源分配對交疊干擾的影響，提高無線通信網絡系統應對密集交疊干擾場景的資源分配能力。

1) 狀態：6G DN 所有可能的通信鏈路資源分配狀態的集合，即狀態集。因此，6G DN 狀態可以表示為

其中，Kt表示通信鏈路的資源分配狀態。

2) 動作：6G DN 觀察當前狀態做出相應通信鏈路資源分配的集合，即動作集。動作集的大小為通信鏈路的數量M與最大通信資源數量Ms的乘積。因此，6G DN 資源分配動作集可以表示為

3) 獎勵：6G DN 在狀態S執行動作A獲得的對應回報。每個獎勵R和每個狀態-動作對對應，因此，6G DN 獎勵可表示為

其中，ηt表示6G DN 已經使用的通信資源數量。

4) 動作價值函數：6G DN 狀態S和動作A的價值估計，即動作價值函數是基于狀態S和動作A的期望回報。由于6G DN 是根據資源分配策略π進行通信鏈路資源分配的，動作價值函數Qπ(s,a)可以表示為

由于每個狀態都需要窮舉出所有可能的方案，本文提出利用貝爾曼方程來化簡，具體推導過程如式(24)所示。

動作價值函數可以表示為

貝爾曼方程利用時間差法中的Q-Learning算法進行求解。Q-Learning 值的迭代可以表示為

其中，α表示學習率。當系統的狀態和動作數量龐大且連續時，利用Q-Learning 解決時很難實現資源分配策略的收斂。因此，DQN 用一個神經網絡Q（s,a;θ）代替動作價值函數。DQN 的神經網絡參數θ采用梯度下降方法，可以表示為

其中，?θ(·) 表示對權值θ進行梯度運算。此外，在利用神經網絡逼近動作價值函數時，目標值與估計值使用相同權值θ的神經網絡，容易導致訓練網絡不穩定和估值過高。因此，使用一個權值的目標網絡專門用于產生目標值。權值θ的神經網絡專門用于評估策略更新參數。具有雙重權值的神經網絡更新可以表示為

3.2 基于Dueling DQN 的資源分配算法

本文所提的基于Dueling DQN的資源分配算法采用競爭網絡模型結合MDP來解決交疊干擾問題。競爭網絡可以有效提取6G DN 密集交疊干擾的特征。算法的時間復雜度只與競爭網絡模型的規模有關，受實際的無線通信環境影響較小。其次，利用MDP 來解決資源分配問題，將原本的CO 問題轉成序列決策問題求解，大大降低直接求解優化問題的難度。

為防止DQN 估值過高，利用競爭網絡進一步提高算法網絡學習的魯棒性。競爭網絡將動作價值函數Q(s,a)分成狀態價值函數V(s)和優勢函數Α(s,a)。Α(s,a)表示在狀態s下選取資源分配動作a的合理性。競爭網絡的動作價值函數可表示為

其中，NA=MMs表示所有資源分配動作的數量。

本文提出基于Dueling DQN的資源分配算法來解決6G DN 無交疊干擾分配問題。算法結構如圖7所示，算法包含6G DN 環境、ε-greedy 策略、深度Q 網絡、目標Q 網絡、損失函數、經驗池和抽樣小批量樣本。其中，6G DN 環境提供環境狀態S和根據動作更新通信鏈路的狀態；ε-greedy 策略為深度Q 網絡提供“探索-利用”的能力；深度Q 網絡評估動作的價值；目標Q 網絡則選擇當前價值最大的動作；經驗池和抽樣小批量樣本則增加樣本之間的隨機性；損失函數根據式(28)對深度Q 網絡的網絡參數進行更新。

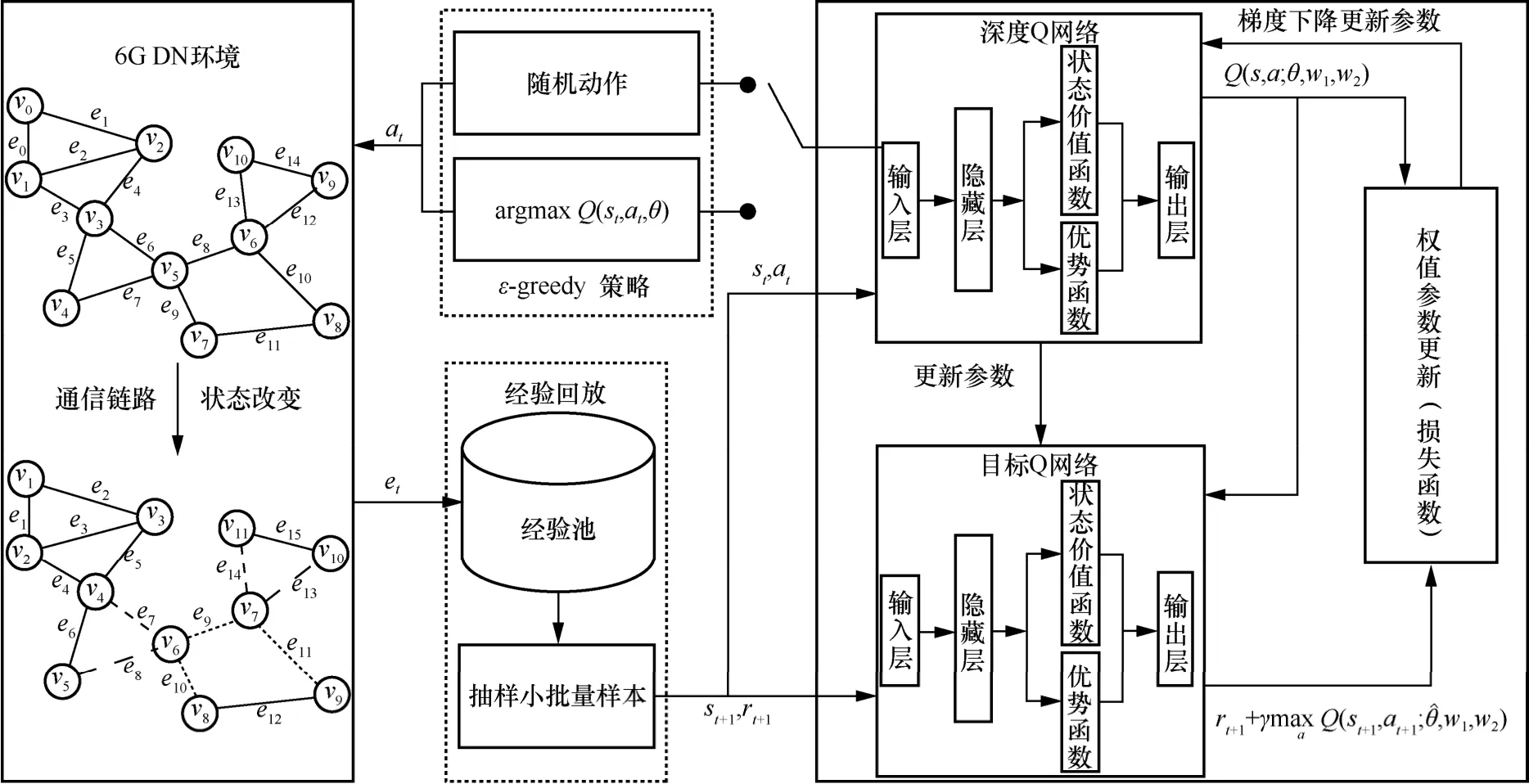
圖7 基于Dueling DQN 的資源分配算法結構

基于Dueling DQN 的資源分配算法如算法1所示。

算法1基于Dueling DQN 的資源分配算法

輸入網絡拓撲G(V,E)，獎勵折扣因子γ，經驗回放大小ND，目標網絡更新頻率L，學習率α，樣本批采樣大小Γ，訓練次數Ntrain，每次訓練執行時間長度T

輸出神經網絡權值θ，w1，w2

4 仿真結果與性能分析

實驗采用的硬件平臺為個人計算機，CPU 為Intel(R) Xeon(R) Gold 6242R CPU @ 3.10 GHz，GPU 為NVIDIA RTX 3080Ti，內存為64 GB。隨著通信鏈路數量增加，網絡復雜度和密集程度增加。

根據表1 參數進行仿真實驗，分別得到本文算法與其他3 種算法網絡吞吐量和資源復用率性能的對比實驗數據。其中，對比算法1 為無競爭網絡的深度Q 網絡算法，對比算法2 為基于隨機匹配的資源分配算法，對比算法3 為基于貪婪匹配的資源分配算法。

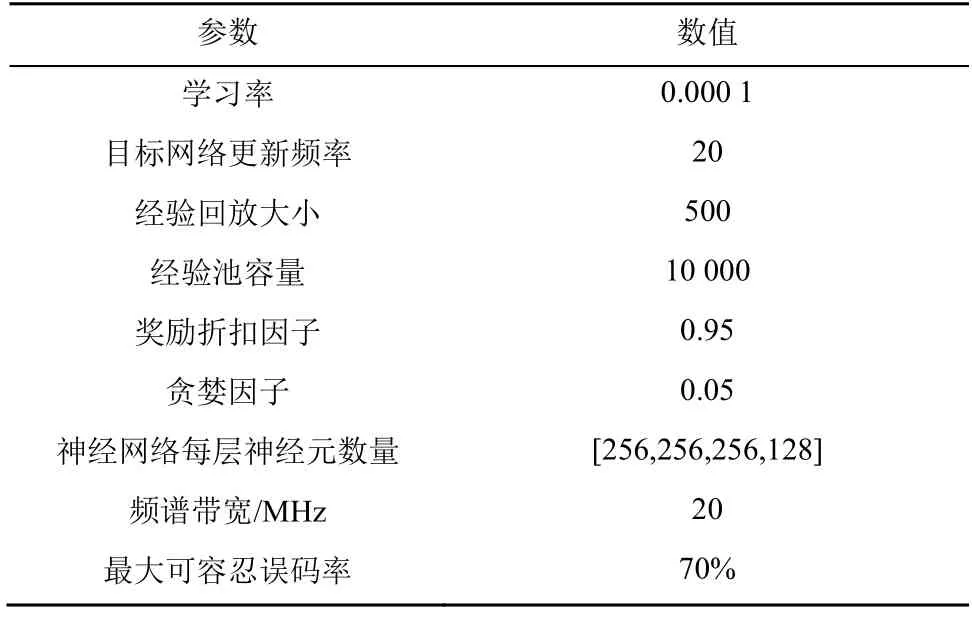
表1 仿真參數設置

4.1 時間復雜度分析與算法對比

本文算法和對比算法1 的時間復雜度主要由神經網絡的權值迭代決定，時間復雜度分別為O(G1L1)和O(G2L2)。其中，G表示神經網絡的隱藏層數；L表示每層神經元的數量。對比算法2 的時間復雜度由通信鏈路數量和通信資源決定，但每次分配資源優先考慮資源無沖突，因此時間復雜度為O(MMs)。對比算法3 的時間復雜度由通信鏈路數量和通信資源決定，但每次分配資源優先考慮復用資源，時間復雜度為O(Mlog(Ms))。

本文算法和對比算法1 在神經網絡的隱藏層數和每層神經元的數量相近時，兩者時間復雜度近似。但本文算法采用競爭網絡架構，將動作價值函數分成狀態價值函數和優勢函數，當通信鏈路或通信資源的數量改變時，只改變對應的神經網絡權值即可。而無競爭網絡的對比算法1 則需要進行整體改變。因此隨著6G DN 的網絡規模的增加，本文算法的實際時間復雜度會低于對比算法1。對比算法2 和對比算法3 直接受到通信鏈路和通信資源的數量影響，兩者的時間復雜度隨著6G DN 的網絡規模的增加而線性增加。

綜上所述，相對于傳統資源分配算法，深度強化學習算法在時間復雜度方面有著穩定的優勢。由于神經網絡可以更好地適應6G DN 的網絡規模的動態變化，時間復雜度只與神經網絡模型的大小有關，受實際的無線通信環境影響較小。因此使用基于Dueling DQN 的資源分配算法可以更好地解決6G DN 下的密集交疊干擾問題。

4.2 競爭網絡結構的效能分析

為驗證本文所提出的基于Dueling DQN的資源分配算法在通信鏈路數量較大的情況下所產生的優化效果，本文主要從每次方案中的累積回報U進行實驗驗證。累積回報U可表示為

如圖8 所示，基于Dueling DQN 的資源分配算法的累積回報隨著迭代次數的增加而變化。其中，本文算法相比無競爭網絡結構的算法探索資源分配策略的速度更快，累積回報曲線上升的趨勢更加迅速。圖8 中有競爭網絡結構的算法得到的累積回報值高，表明有競爭網絡結構可有效處理交疊干擾和優化資源分配，即網絡吞吐量和資源復用率更高。

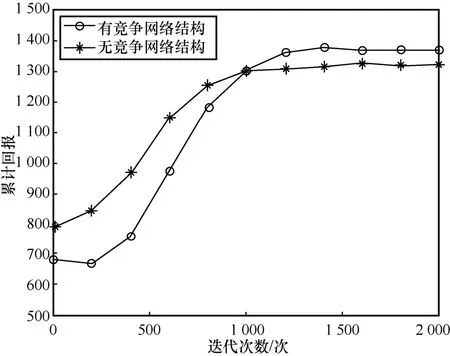
圖8 競爭網絡效果

4.3 6G DN 的性能評價指標

1) 網絡吞吐量。該性能指標可評價資源分配算法分配完所有通信鏈路資源后6G DN 的網絡吞吐量[22]，表示為

2) 資源復用率。該性能指標可評價資源分配算法使6G DN 所有通信鏈路交疊無干擾后6G DN 的通信資源復用率[23]，表示為

其中，η*為最終使用的通信資源數量。

4.4 網絡吞吐量性能對比

圖9 為本文算法和3 種對比算法在不同通信鏈路數量下的最大網絡吞吐量。隨著通信鏈路數量的增加，通信系統中的IT 交疊區變多，4 種算法得到的最大網絡吞吐量整體都呈現上升趨勢。對比算法1、對比算法2 和對比算法3 得到的最大網絡吞吐量明顯低于本文算法。當通信鏈路數量為20、35、40 時，有競爭網絡結構的本文算法相對于對比算法1 提高20%及以上的網絡性能。這表明本文算法可有效提高網絡吞吐量和處理干擾能力的上限。

圖10 為本文算法和3 種對比算法在不同通信鏈路數量下的最小網絡吞吐量。隨著通信鏈路數量的增加，本文算法和3 種對比算法得到的網絡吞吐量呈現上升趨勢。本文算法和對比算法1 相對于對比算法2、對比算法3 有效提高了最小網絡吞吐量。其中，有競爭網絡結構的本文算法相對于對比算法1 提高5%及以上的網絡吞吐量。這表明競爭網絡結構可有效地提高系統處理交疊干擾能力的下限。

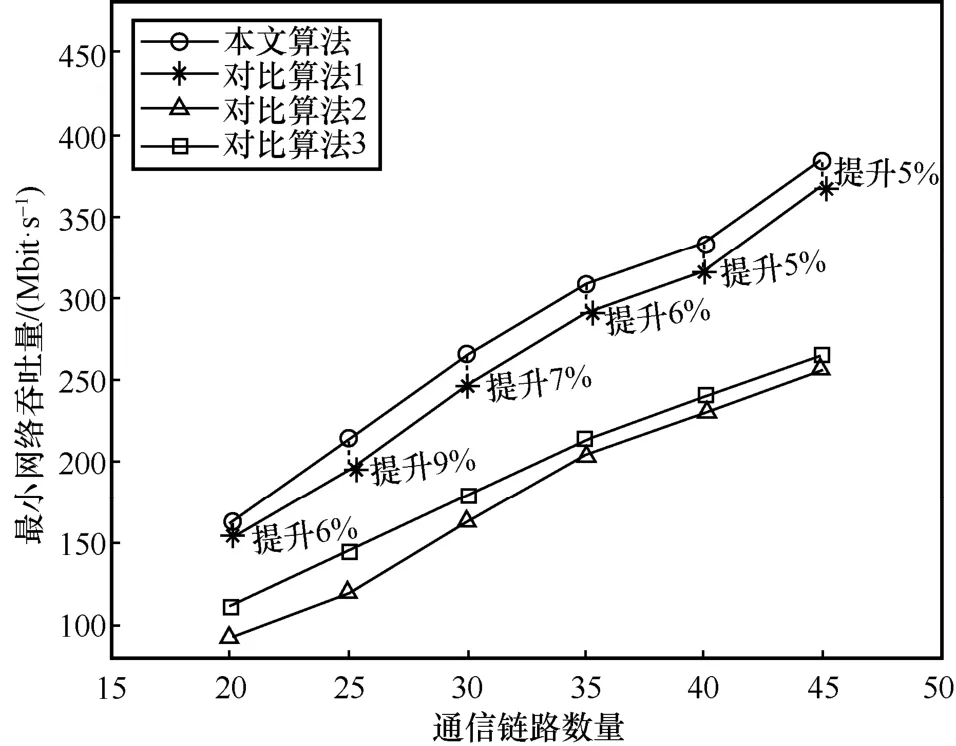
圖10 6G DN 最小網絡吞吐量

圖11 為本文算法和3 種對比算法在不同通信鏈路數量的平均網絡吞吐量。隨著通信鏈路數量的增加，本文算法得到的網絡吞吐量呈現穩定上升趨勢。本文算法得到的平均網絡吞吐量明顯高于對比算法2 和對比算法3，且相對于對比算法1 提高6%及以上的網絡吞吐量。

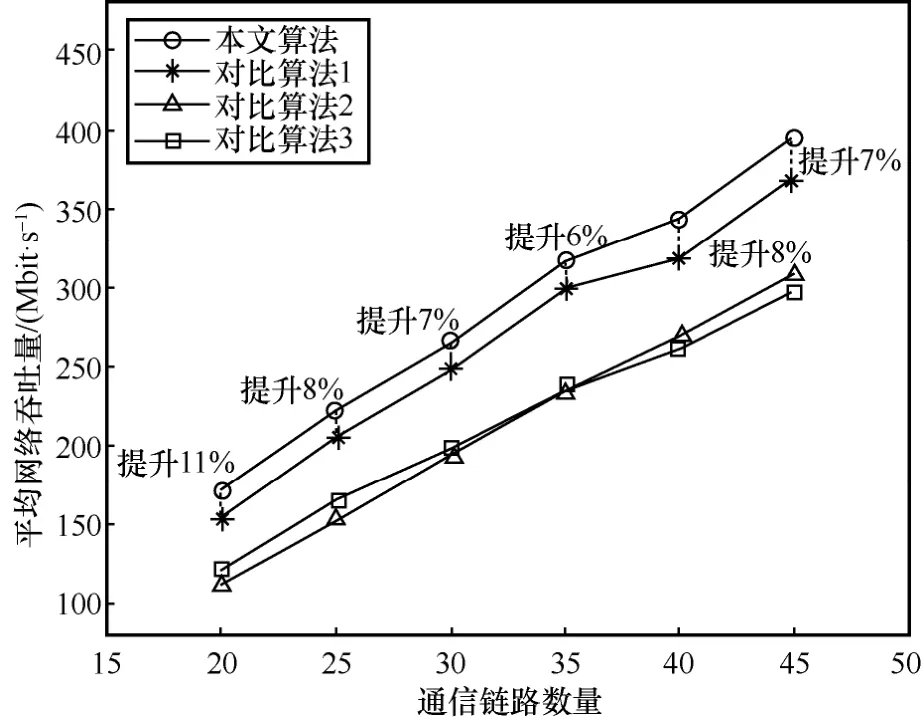
圖11 6G DN 平均網絡吞吐量

針對網絡吞吐量，本文所提基于Dueling DQN 的資源分配算法利用DRL 的在線決策能力，降低計算所需的內存消耗（將網絡狀態作為競爭網絡的輸入得到資源分配策略的輸出），其中，競爭網絡提取小區間無交疊干擾狀態，通過資源分配實現小區間無交疊干擾，從而大幅度提高網絡吞吐量，保證網絡的穩定性。

4.5 資源復用率性能對比

圖12 為本文算法和3 種對比算法在不同通信鏈路數量下的最大資源復用率。隨著通信鏈路的增加，本文所提的基于Dueling DQN 的資源分配算法得到的整體資源復用率明顯高于其他算法。其中，本文算法比對比算法1 提高19%的最大資源復用率；相較于對比算法2 和對比算法3 分別提高25%和26%的最大資源復用率。這表明本文采用MDP 解決資源分配問題，可有效增加整個系統資源分配能力的上限。圖12～圖14 中，不同橫線表示不同算法在5 次不同通信鏈路數量的資源復用率均值。

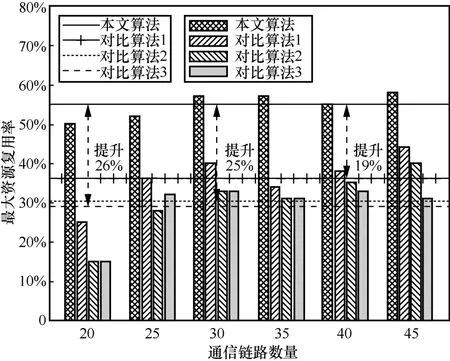
圖12 最大資源復用率

圖13 為本文算法和3 種對比算法在不同通信鏈路數量的最小資源復用率。隨著通信鏈路的增加，本文算法和對比算法1 得到的最小資源復用率明顯高于對比算法2、對比算法3。其中，本文算法比對比算法1 提高6%的最小資源利用；相較于對比算法2和對比算法3 分別提高37%和31%的最小資源復用率。這表明本文算法可提高資源分配能力的下限。

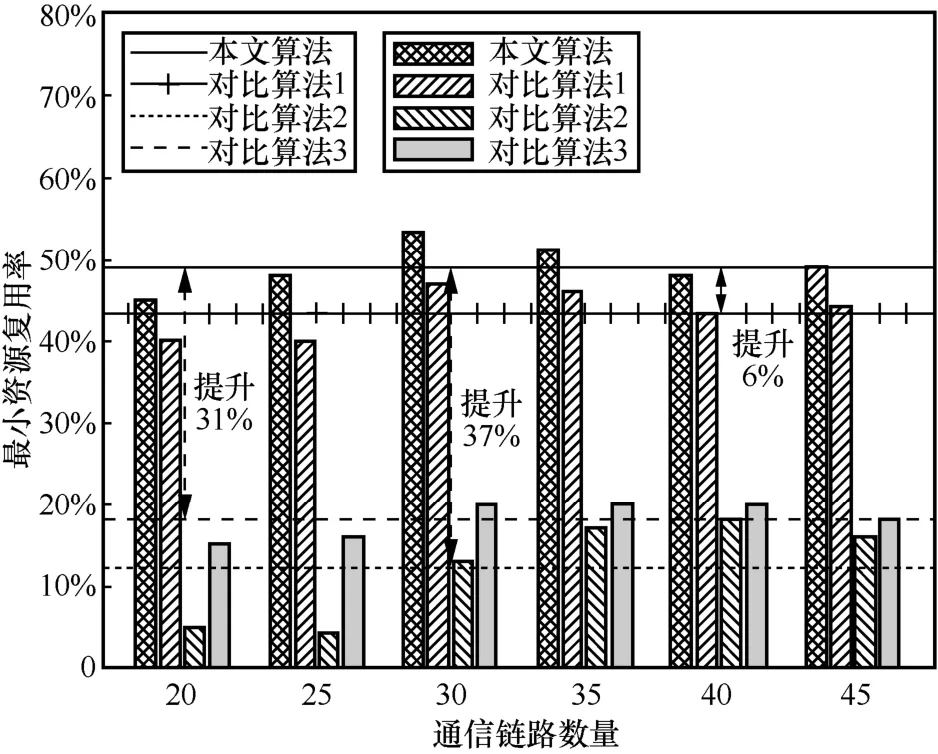
圖13 最小資源復用率

圖14 為本文算法和3 種對比算法在不同通信鏈路數量的平均資源復用率。隨著通信鏈路數量的增加，4 種算法得到的平均資源復用率處于平穩波動狀態。其中，本文所提的基于Dueling DQN 的資源分配算法比對比算法1 提高7%的平均資源復用率；相較于對比算法2 和對比算法3 分別提高27%和26%的平均資源復用率。這表明本文算法可有效提高系統資源分配能力。

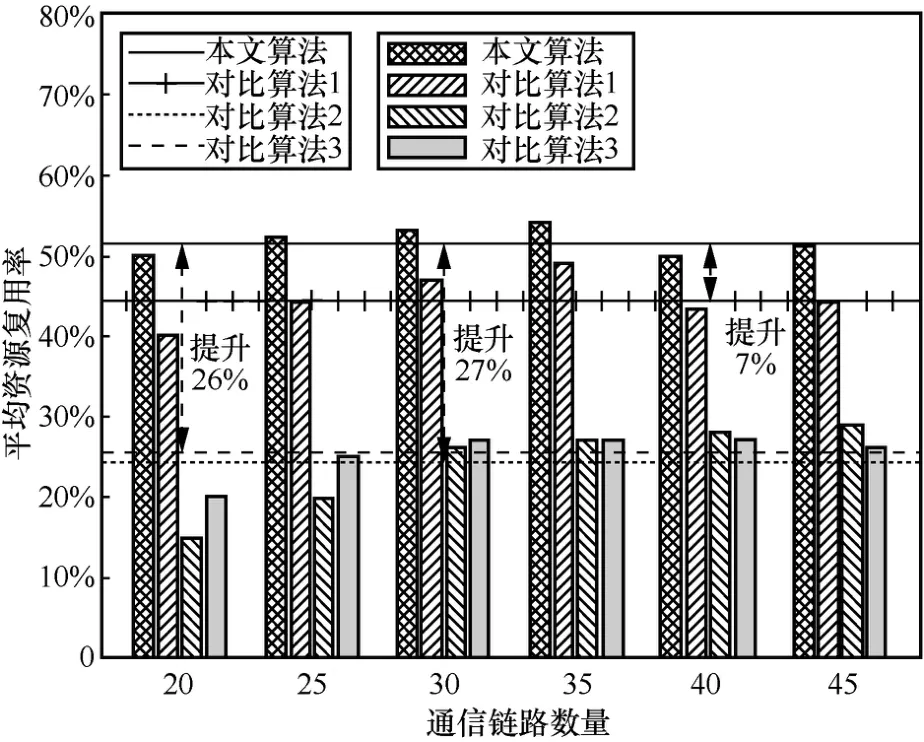
圖14 平均資源復用率

針對資源復用率，本文所提基于Dueling DQN的資源分配算法利用MDP 能夠實時掌握網絡的運作狀態（為每一時刻的狀態提供一個對應資源分配動作），找到一種滿足實時性和資源效率要求的資源分配策略，增強資源分配能力，提高通信資源復用率。

4.6 仿真測試與實際測試對比

實際測試采用戴爾（DELL）X86 服務器、美國國家儀器公司（NI,national instruments）通用軟件無線電外設N310 硬件平臺和歐洲電信學院的開源空口（OAI,open air interface）。根據6G DN相關文章中的仿真場景，搭建密集網絡[24-25]，并按照所提算法中的參數來配置實際密集網絡系統的參數，如表2 所示。

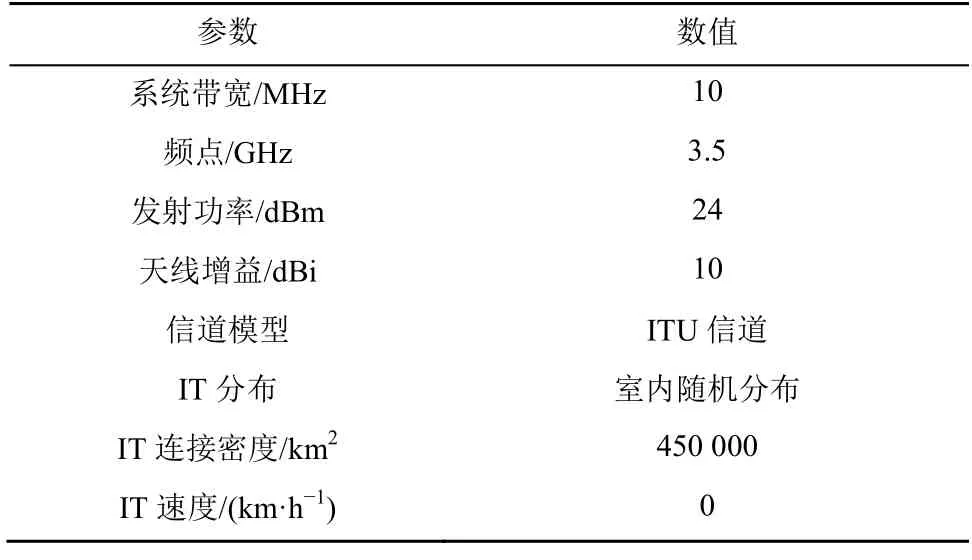
表2 密集網絡系統的參數

如圖15 所示，隨著通信鏈路數量的增加，網絡吞吐量整體都呈上升趨勢，其中，本文算法仿真得到的網絡吞吐量始終大于實際通信環境的測試結果。基準算法的實際測試結果明顯低于本文算法的實際測試結果。當通信鏈路數量為45 時，本文算法比基準算法最大提高37%的網絡吞吐量；當通信鏈路數量為30 時，本文算法比基準算法最小提高17%的網絡吞吐量。通過部署基于Dueling DQN的資源分配算法可以降低交疊干擾，提高網絡吞吐量。實際測試結果驗證了本文算法的有效性。

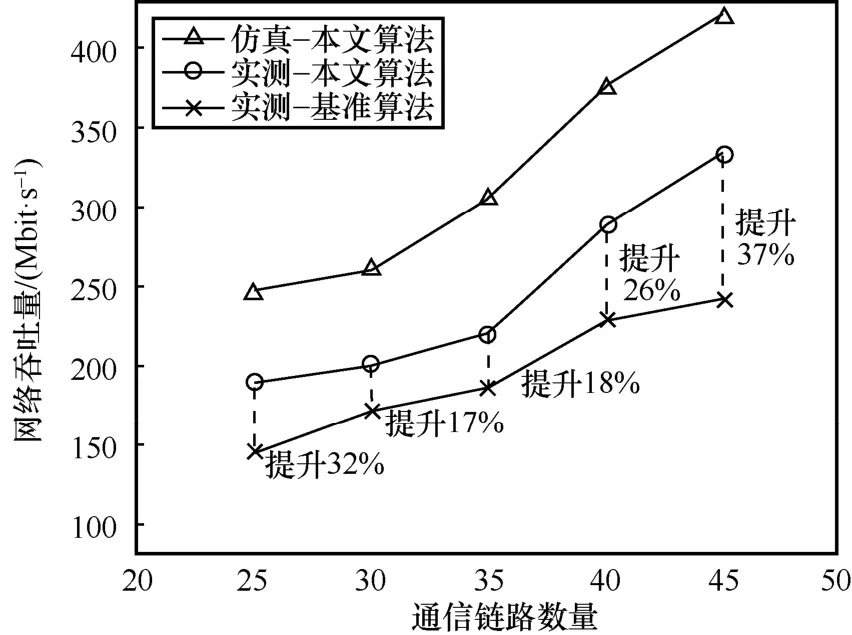
圖15 實際測試結果

5 結束語

為通過資源分配實現小區間無交疊干擾，提高6G DN 的網絡性能，本文討論了6G DN 中的資源分配問題，但資源受限和節點密集分布導致難以通過傳統的優化方法解決資源的有效分配問題。針對此問題，本文提出了基于Dueling DQN 的資源分配算法。該算法利用在線決策的能力彌補以犧牲存儲空間來提高網絡吞吐量的資源分配技術缺點，比優化方法有更少的內存消耗。仿真實驗結果表明，所提算法可以有效提高網絡吞吐量和資源復用率，并且隨著網絡規模和密集程度的增加對方法的實時性和內存消耗的影響較小，資源復用率處于穩定狀態。在實際測試中，本文算法比基準算法最大提高了33%的網絡吞吐量和37%的資源復用率，有效提升了網絡性能。