超臨界二氧化碳壓縮機性能不確定性量化研究

馬 燦,代 路,呂偉劍,張克龍,*

(1.熱能動力技術重點實驗室,湖北 武漢 430205;2.武漢第二船舶設計研究所,湖北 武漢 430205)

超臨界二氧化碳(S-CO2)循環在核電領域具有良好的應用前景,近年來得到了越來越多的研究[1-2]。壓縮機是S-CO2動力循環中的關鍵設備,其性能對動力循環特性有較大的影響。在二氧化碳反應堆一回路中,壓縮機是工質循環的關鍵設備,直接決定了一回路系統的耗功,在二氧化碳二回路系統中,壓縮機是工質壓縮的關鍵設備,對二回路系統的熱功轉換效率有著較大影響。

由于加工制造誤差和系統狀態波動,S-CO2壓縮機設計和運行參數存在不可避免的隨機波動,如葉片前緣半徑、表面粗糙度、動靜間隙等幾何參數的隨機波動以及進氣壓力、溫度、轉速等運行參數的隨機波動。這些隨機變量對S-CO2壓縮機的氣動性能具有不可忽略的影響。運行參數方面,S-CO2壓縮機進口狀態通常接近工質臨界點,由環境溫度、系統負荷等變化引起的進口狀態微小變化會造成工質物性的較大變化,局部溫度和壓力降低還會導致亞臨界狀態甚至冷凝的出現,使得氣動性能波動較大。

受限于試驗條件的限制,國內外開展的S-CO2壓縮機實驗研究[3-4]和積累的實驗數據較少,主要研究手段是數值模擬,通過求解雷諾平均Navier-Stokes(RANS)方程、基于物性表格插值獲取S-CO2物性開展S-CO2壓縮機內部流動仿真[5]和流動機理分析[6],進一步考慮相變模型[7]、非定常效應對流動的影響[8-9]。針對S-CO2壓縮機靠近流體臨界點運行時易出現相變的問題,國內開展了S-CO2壓縮機葉頂兩相流[10]、葉輪內部凝結性能分析[11],以及跨臨界CO2壓縮機冷凝特性[12]、進口干度與氣動性能關聯性分析[13],并發展了考慮S-CO2物性的多變功計算方法[14]。雖然近年來開展的一系列實驗和數值研究表明S-CO2壓縮機氣動性能對進氣參數變化的敏感性較大,目前國內外缺乏關于隨機參數波動對S-CO2壓縮機氣動性能影響的定量研究。

準確預測S-CO2壓縮機的變工況性能對于S-CO2動力循環的熱力分析具有重要意義。本文對某S-CO2離心壓縮機進行氣動性能預測,分別采用一維經驗模型方法和三維CFD仿真方法,并基于三維CFD仿真結果,采用任意多項式混沌(aPC)方法[15-16]對進口總溫波動引起的S-CO2壓縮機氣動性能不確定性進行定量研究。

1 數值方法

1.1 一維經驗模型

一維經驗模型采用商業軟件NREC COMPAL,壓縮機葉輪采用兩區模型,將葉輪內部流動分為射流區和尾跡區分別建模[17]。采用了3種擴散比建模方法:Two-Element-In-Series模型(一維模型A)、backbone curve模型(一維模型B)和hybrid function模型(一維模型C),3種方法均依賴于經驗關聯式,其中Two-Element-In-Series將葉輪內部分為前后兩段建模,前段簡化為擴壓器或噴嘴,后段簡化為擴壓器,兩段的性能通過經驗給定;backbone curve模型首先通過等熵流動假定計算出理想的擴散比,然后根據經驗關聯式得到實際的擴散比;hybrid function模型首先參照backbone curve模型計算出擴散比,隨后根據葉輪幾何參數對前后兩段的性能進行經驗修正,以兼顧設計點和非設計點的性能預測。

1.2 三維CFD模型

三維CFD采用商業軟件NUMECA/Fine-Turbo求解三維定常Navier-Stokes方程。S-CO2流體物性基于NIST數據庫。空間離散采用二階中心格式,湍流模型采用雙方程k-ωSST模型,動靜交界面采用混合平面法。

1.3 不確定性量化方法

考慮概率空間(Ω,Λ,Γ)內的隨機過程,其中Ω為樣本空間,Λ為Ω的子集,Γ為概率,對于隨機函數Y=f(ξ),ξ∈Ω的一維多項式混沌展開可以寫成:

(1)

其中:d為展開階數;ci為展開系數;Ψi為正交多項式。展開系數可以由式(2)計算:

(2)

求解可采用Galerkin投影方法、配點法或數值積分法。本文采用高斯積分法計算多項式展開系數。對階數不超過2p+1的多項式g(ξ),可以找到p+1個最佳高斯配置點ξk及權重wk,從而準確計算其積分:

(3)

與Ahlfeld等[16]的方法類似,最佳高斯配置點及權重根據隨機輸入參數的統計矩采用Mysovskikh[18]推導的矩陣變換關系計算得到。對于連續型隨機變量ξ∈Ω,k階統計矩μk的表達式為:

(4)

對于離散型隨機變量ξ∈Ωh,假定概率密度函數為w,k階統計矩的表達式為:

(5)

對于有ND個采樣點的數據集,k階統計矩的表達式為:

(6)

確定正交多項式的展開系數后,Y的統計信息可通過展開系數計算得到,如均值μY和方差σY的表達式為:

μY=c1

(7)

(8)

1.4 壓縮機參數

本文研究了某100 kW級S-CO2離心壓縮機,子午面型線如圖1所示,該壓縮機由葉輪和一排通道式擴壓器組成。葉輪葉頂間隙為出口葉高的17%。葉輪葉片數為12,其中一半葉片為分流葉片,擴壓器葉片數為18。壓縮機氣動設計參數列于表1,幾何造型如圖2所示。

表1 S-CO2壓縮機設計參數

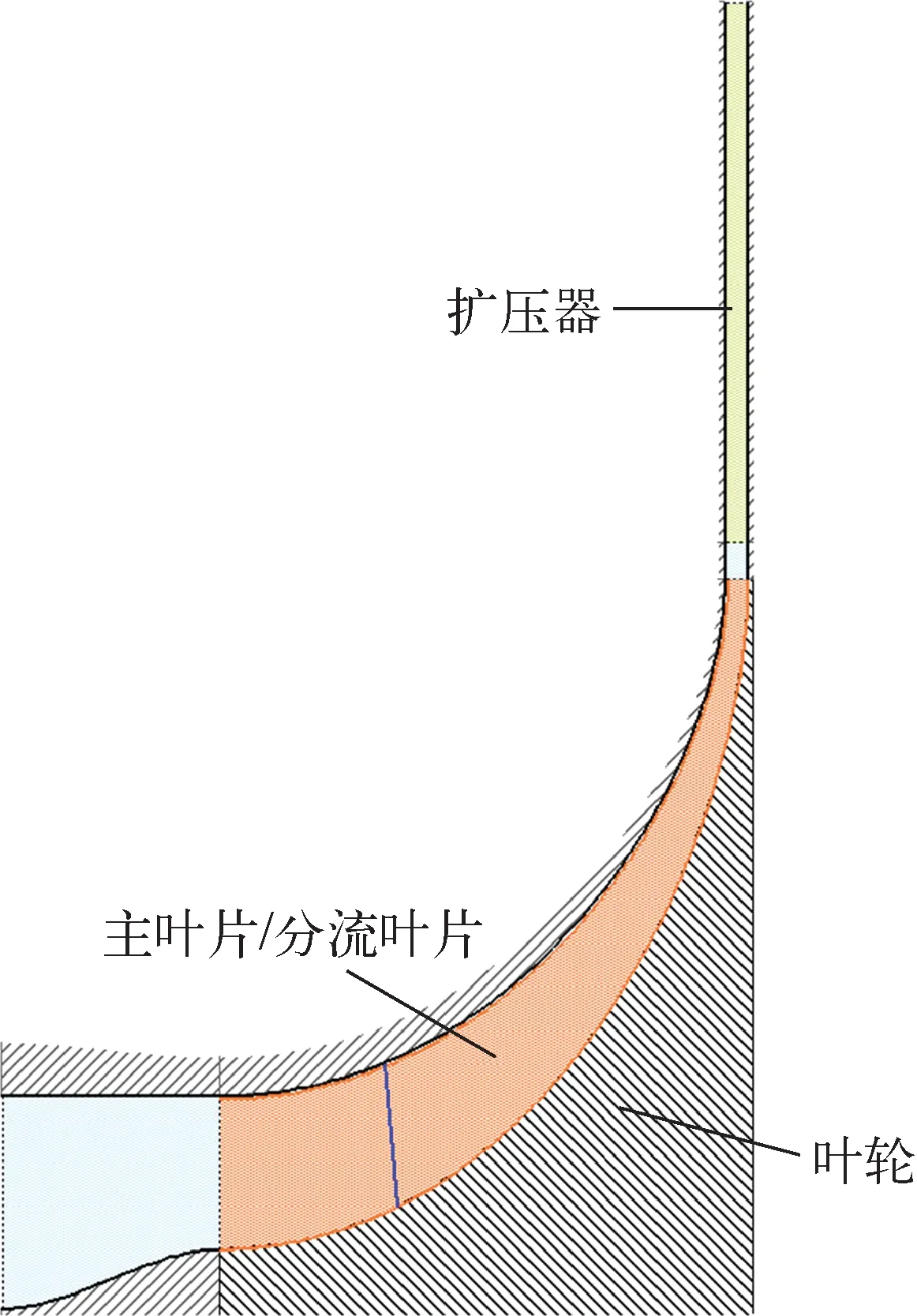
圖1 S-CO2壓縮機子午面型線

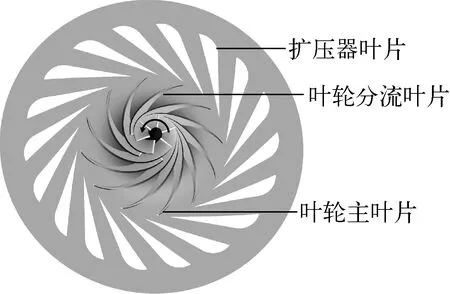
圖2 壓縮機幾何造型

三維CFD計算網格如圖3所示,總網格數為248萬,其中葉輪通道網格數為139萬,擴壓器通道網格數為109萬,壁面y+小于1,以便于采用低雷諾數湍流模型對近壁面流動進行求解。除該基準網格外,分別采用較粗和較密的網格開展了三維CFD計算,計算得到的流量和效率對比列于表2。由表2可見,基準網格計算得到的流量和效率與密網格的相對偏差分別為0.1%和0.07%,對于本文關注的壓縮機性能參數而言,采用基準網格能夠得到足夠精確的結果,因此本文三維CFD計算采用圖3所示的網格。

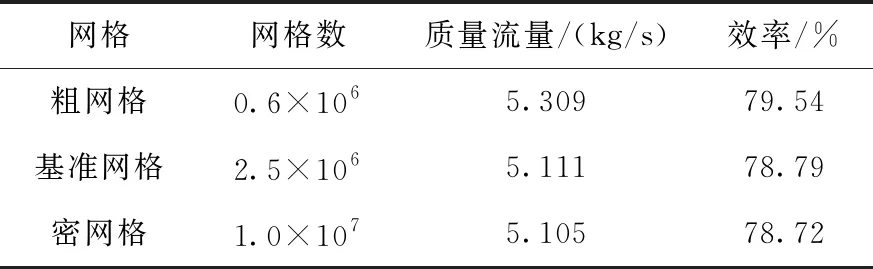
表2 不同網格數計算結果

圖3 三維CFD計算網格

2 數值結果

2.1 變工況特性

一維模型在給定進出口條件后根據壓縮機葉輪的進出口半徑、葉高、葉片角以及擴壓器進出口半徑、葉高、擴張角、喉部面積等參數,基于簡化模型和大量試驗數據總結得到的經驗關聯式計算壓縮機性能參數。CFD和一維模型的壓縮機變工況特性曲線預測結果如圖4所示。根據CFD結果,從80%到100%設計流量,壓縮機效率變化低于1%,最高效率為79.2%,在93%設計流量處產生。根據一維模型A和B的計算結果,最高效率點在80%設計流量處,隨后效率隨流量增加而緩慢下降。根據一維模型C的計算結果,在圖4中的流量范圍內,效率隨流量的增加而降低。隨著流量的增加,CFD和一維模型的預測結果都是壓比降低。總的來看,不同一維模型預測得到的效率和壓比都與CFD結果有顯著差異。一維模型的優勢是計算速度快,但其計算結果受經驗關聯式影響較大,目前廣泛采用的經驗關聯式多基于理想氣體試驗結果,由于目前S-CO2壓縮機試驗數據較為欠缺,現有商業軟件中壓縮機一維模型經驗關聯式針對S-CO2壓縮機內部超臨界流體流動的準確性尚未經過系統性驗證;而三維CFD計算采用了更準確的幾何模型,流動模型所做的簡化也遠少于一維模型,因此,本文開展的壓縮機性能不確定性量化研究基于CFD計算結果開展。

2.2 進口溫度波動影響

由于S-CO2壓縮機進氣參數接近工質臨界點,由環境溫度、系統負荷等變化引起的進口狀態微小變化會造成工質物性的較大變化,從而對壓縮機的性能產生影響。對于S-CO2循環系統,隨著季節和區域造成的外部冷卻水溫度變化,壓縮機進口溫度也會產生變化。為了研究進口狀態變化對性能的影響,本文以冷卻水溫度變化造成壓縮機進口溫度變化4 K為例,將壓縮機的進口總溫在設計值的基礎上變化±2 K,其他參數不變,對其流動進行了定常計算。

中葉展截面的熵分布如圖5所示,分別對比了設計工況和進口總溫變化(ΔTt)為±2 K的結果。圖5中,s/s0為基于流場中最大熵值s0歸一化處理的熵。設計工況下葉輪和擴壓器葉片的攻角都接近0°,進口總溫增加2 K后,葉輪和擴壓器都出現了較大的負攻角,擴壓器葉片壓力面的高損失區域增大,出現了較為明顯的高熵區;進口總溫減少2 K后,攻角變為正,擴壓器葉片吸力面附近出現了較為明顯的高熵區。可見,當進口總溫變化時,在相同的壓比下,壓縮機內部的熵分布出現了明顯的變化,反映在流場上主要是由壓縮機流量變化引起了葉片攻角變化,進而造成內部流動損失的變化。

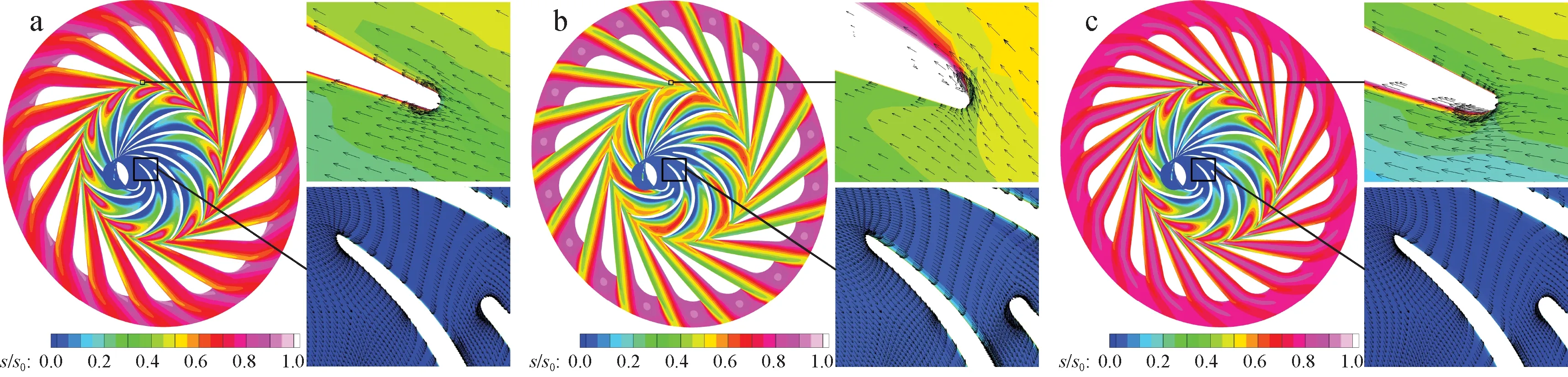
a——ΔTt=0 K;b——ΔTt=-2 K;c——ΔTt=2 K

等熵效率和流量隨進口總溫的變化如圖6所示。進口總溫增加2 K以內,等熵效率的變化幅度較小,不超過0.4%;當進口總溫減小時,等熵效率大幅下降,進口總溫減小2 K時下降了11.7%。與效率類似,進口總溫對流量的影響也很顯著。總的來說隨著進口總溫的增加流量減小。與設計工況相比,進口總溫增加2 K時流量減少了27%,進口總溫減少2 K時流量增加了62%。總的來說,當進口總溫減少時,性能的變化幅度比進口總溫增加時要大。

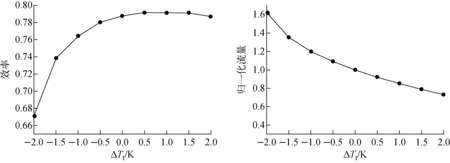
圖6 壓縮機氣動性能隨進口總溫的變化

可見,進口總溫變化對工質物性的影響造成了S-CO2壓縮機流量產生了顯著變化,從而對葉片攻角、流動損失造成了顯著影響,這一影響反映在效率的變化上,這也是相對于理想工質而言,S-CO2壓縮機對進口參數敏感性更高的原因。

2.3 壓縮機氣動性能不確定性量化

進口總溫波動對S-CO2壓縮機性能有著不可忽視的影響。在S-CO2循環系統中,壓縮機進口狀態的變化可能由環境溫度、系統負荷等變化引起,必須在系統性能分析和壓縮機設計中加以考慮。系統狀態變化的測量數據通常是有限且離散的數據集,難以得到其真實概率密度分布函數,采用aPC方法可以基于離散數據集的統計矩進行不確定性量化分析,從而避免了擬合概率密度分布函數引起的誤差。本文采用aPC方法對進口總溫隨機波動引起的S-CO2壓縮機性能不確定性進行了量化。

進口總溫的變化假定由系統狀態波動引起,在±2 K的變化范圍內分布了99個采集數據點,如圖7所示。由于數據十分有限,很難對其概率密度函數進行準確擬合,而任意多項式方法基于數據的統計矩進行多項式展開,因此同時適用于連續分布以及離散的數據集。

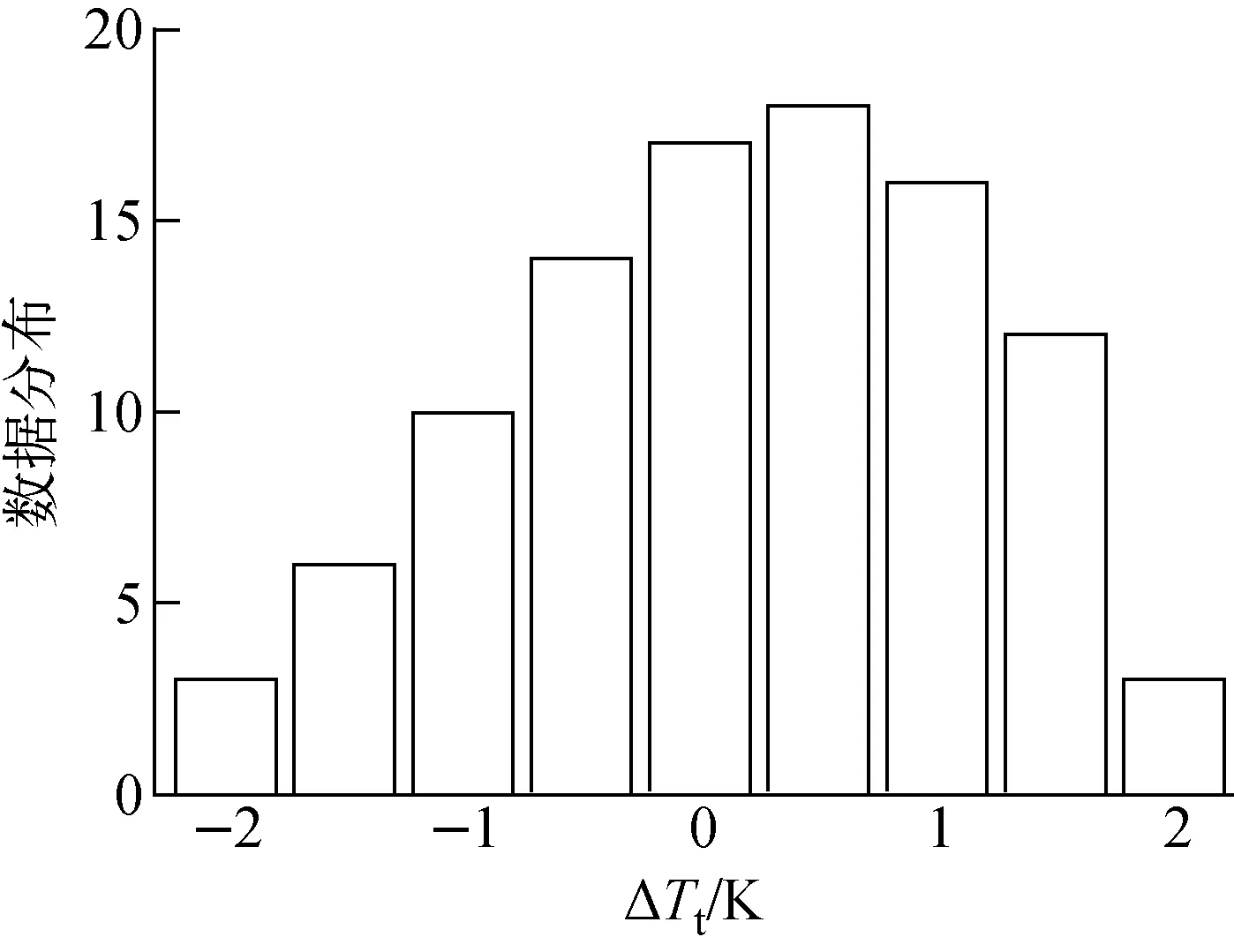
圖7 進口總溫變化隨機數據分布

由于離散數據集中每一個點的壓縮機性能都可以計算得到,因此性能參數的真實統計矩可以準確計算得到,以此作為參照評價aPC方法的準確性。不同階數aPC方法的計算誤差如圖8所示,采用1階多項式展開時,效率和流量均值的計算相對誤差不超過1%,當階數增加到4階時,相對誤差不超過0.01%。效率和流量方差的計算誤差總的來說大于均值,采用1階多項式展開時,效率方差的相對誤差達到73%,流量方差的相對誤差達到23%。當階數增加時,方差的計算誤差降低,采用4階多項式展開時,效率方差的計算相對誤差為3.2%,流量方差的計算相對誤差為2.1%。可見,采用aPC方法能夠較好地預測性能參數的均值和方差,采用4階多項式展開時,預測相對誤差已達到5%以下。

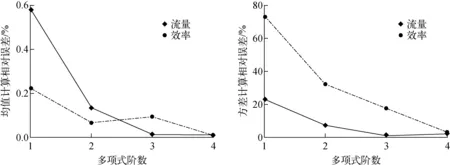
圖8 不同階數aPC方法的相對誤差

3 結論

本文采用一維模型和三維CFD方法對某S-CO2壓縮機進行了數值研究,一維模型預測得到的效率、壓比與三維CFD計算結果存在明顯差異。基于三維CFD計算結果,采用aPC方法對進口總溫波動引起的S-CO2壓縮機氣動性能不確定性進行了定量研究,進口總溫波動范圍為設計工況±2 K,當進口總溫降低2 K時,葉輪和擴壓器攻角由0°變為-6°,導致壓縮機等熵效率降低了11.7%,流量增加了62%。采用離散的測量數據集描述進口總溫的隨機波動時,aPC方法能夠較好地預測性能參數的均值和方差。采用1階多項式展開時,效率和流量均值的計算相對誤差不超過1%,效率和流量方差的計算相對誤差總的來說大于均值,采用4階多項式展開時,效率方差的計算相對誤差為3.2%,流量方差的計算相對誤差為2.1%。

結果表明aPC方法能夠高效準確地預測性能參數的統計信息,尤其是當隨機參數的統計信息有限且離散時。本文算例中進口總溫的微小變化造成了壓縮機流量和等熵效率的顯著變化,表明在S-CO2壓縮機的設計中有必要考慮提高進氣參數不確定性的穩健性,aPC方法通過定量給出參數不確定性對S-CO2壓縮機性能的影響,可用于評價S-CO2壓縮機對進氣參數不確定性的穩健性,為S-CO2壓縮機穩健性優化設計奠定基礎,后續有必要進一步開展試驗研究以驗證本文數值模型對于S-CO2壓縮機性能預測的準確性。