點接觸軸承接觸應力可靠性及靈敏度分析

趙振秀，劉軍

（224057 江蘇省 鹽城市 鹽城工學院 機械工程學院）

0 引言

滾動軸承作為機械系統支承與傳遞載荷關鍵的旋轉元件，其可靠性決定了旋轉機械系統的使用壽命，疲勞磨損和點蝕失效會造成滾動軸承失效，無法正常使用。因此軸承的可靠性直接決定了軸承和機械系統的運行可靠性。國內外很多學者對軸承接觸應力進行了深入研究，主要基于Hertz 理論研究了軸承內部的應力分布情況[1-3]。張廣萍等[4]采用Hertz 理論并考慮實際工況研究了軸承的應力分布；張勝倫等[5]研究并優化了結構參數對接觸應力的影響。目前，鮮有學者針對軸承接觸應力的可靠性及其靈敏度展開研究，其中在軸承接觸應力的可靠性定量分析方面研究更少[6-10]。本文基于Hertz理論對接觸應力計算方法進行精度研究，結合應力-強度干涉理論和二階矩法研究點接觸軸承的動態可靠性；對3 種接觸應力計算方法進行精度驗證和誤差分析，建立點接觸軸承動態可靠性模型，并進行動態可靠性及靈敏度計算與分析。

1 點接觸軸承接觸應力計算

1.1 接觸應力計算模型

根據Hertz 理論，假定球軸承的滾動體與內外圈接觸的表面區域為一旋轉橢圓形，最大壓應力出現在幾何中心，其大小為

接觸區域與接觸應力分布如圖1 所示。由圖1可知，接觸區域SC除中心點最大應力處以外其余點的法向應力為

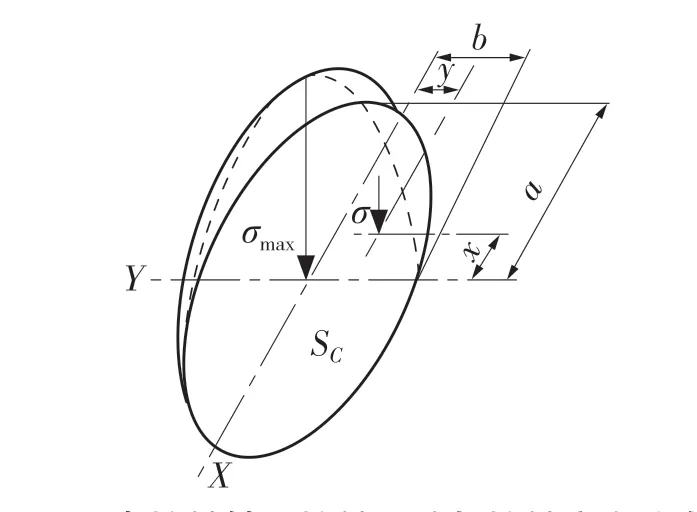
圖1 點接觸軸承接觸區域與接觸應力分布Fig.1 Contact area and contact stress distribution of point-contact bearing

式中：Q——承受載荷；a、b——接觸橢圓的長、短半軸。

式中：a*、b*——接觸橢圓半軸系數；Σρ——曲率和函數；E'——綜合彈性模量。

在載荷Q的作用下，兩物體由于彈性變形而形成接觸區域SC。接觸體表面的位移δ稱為彈性趨近量，定義為

式中：δ*——彈性趨近系數。

式中：v1、v2——彈性接觸體的泊松比；E1、E2——彈性接觸體的彈性模量。

式中：Rix、Riy——滾動體和內（外）圈曲率半徑；i=1、2，1 代表滾動體，2 代表滾道。Rix、Riy示意如圖2 所示。

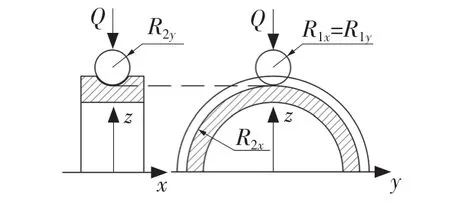
圖2 Hertz 點接觸曲率示意圖Fig.2 Point-contact curvature diagram of Hertz

確定橢圓半軸系數a*、b*和彈性趨近系數δ*為

式中：e——橢圓參數；K(e)，E(e)——第1 類和第2 類完全橢圓積分函數。

1.2 接觸應力的數值計算法

求解軸承接觸應力問題的關鍵是根據曲率函數F(ρ)的值確定橢圓參數e，以及K(e)和E(e)。根據Hertz 理論模型，曲率函數F(ρ)是橢圓半軸a、b的函數

將式（14）變換成式（15）的形式以便求解橢圓參數e

式中：ε——一個微小誤差控制量。

可通過牛頓迭代法求解式（15），獲得e、K(e)和E(e)的值。

1.3 Hamrock-Dowson 經驗法

從式（12）可以看出，當b/a無窮小時，K(e)的收斂很慢，但球軸承點接觸問題恰巧屬于此類情況，因此求解式（15）比較耗時。Hamrock 和Dowson 通過曲線擬合的方法給出了球軸承接觸問題的近似經驗公式為

由式（11）可知

1.4 拉格朗日插值法

基于數值計算法，羅繼偉等[2]設計了一種單向均分法，便捷地獲取軸承點接觸參數；楊咸啟[1]、Harris 等[3]給出了點接觸半軸系數的參數表。根據上述學者的參數表繪制出觸參數變化曲線，如圖3所示，可見3 種參數表的變化趨勢一致。采用拉格朗日二次插值公式，根據上述3 個參數表對半軸系數直接插值計算對應的y。由于點接觸軸承的橢圓參數e接近于1，所以取部分參數如表1 所示，表中的第1 列數據標記為xi，需計算的某一列數據標記為yi，當已知x（xi-1＜x＜xi+1）時可以計算對應的y值

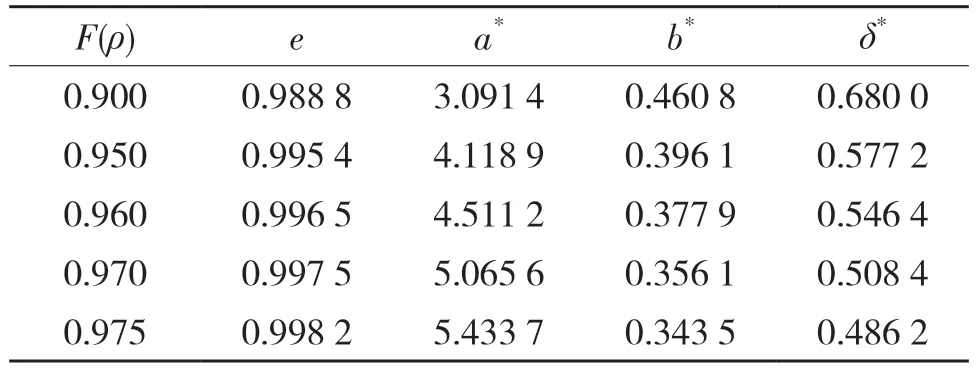
表1 無量綱接觸參數Tab.1 Dimensionless contact parameters

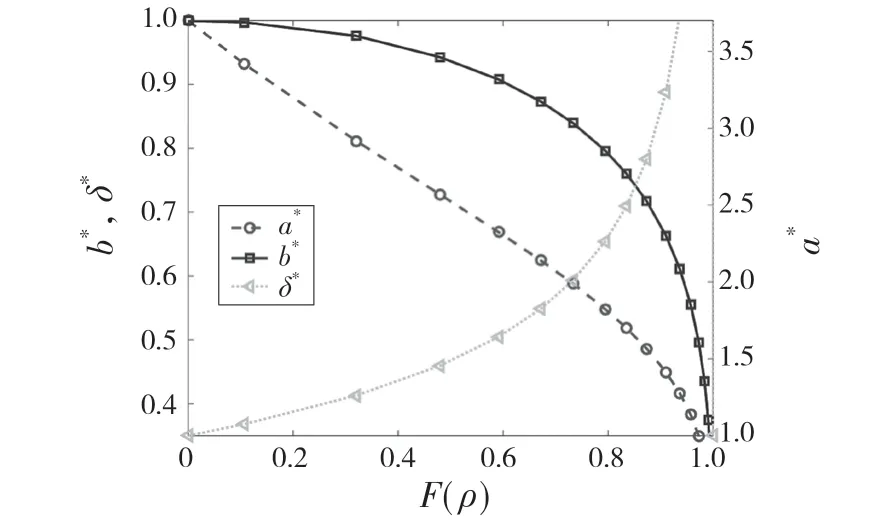
圖3 無量綱接觸參數變化Fig.3 Changes of dimensionless contact parameters

根據上述3 種不同的參數表結合Harris 等[3]的研究，對B218 角接觸球軸承，計算點接觸參數和內、外滾道最大法向接觸應力，結果如表2 所示。對比結果可知：與數值解相比，3 種參數表的誤差均不超過3%。其中文獻[1]的參數表計算的結果更加準確。點接觸軸承內滾道接觸應力大于外滾道，這與文獻[3]研究結果一致，因此，可靠性及靈敏度分析部分僅討論內滾道接觸應力。

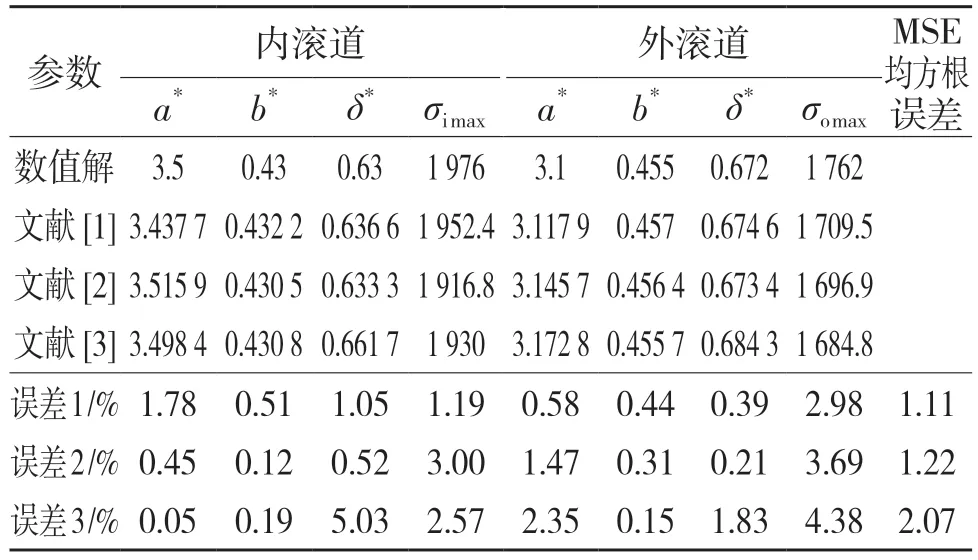
表2 拉格朗日插值法參數表誤差分析Tab.2 Error analysis of Lagrange interpolation parameters

1.5 方法驗證及誤差分析

某機械旋轉系統中，鋼球與內滾道接觸過程中，深溝球軸承鋼球承受徑向載荷為Q=1.5 kN 的靜態載荷，系統運行過程中，同時承受最大徑向載荷為2 kN 的動態載荷。已知鋼球與內滾道的參數如表3 所示。采用上節所述3 種方法求解得出鋼球與內滾道的最大接觸應力隨徑向載荷的變化趨勢如圖4 所示。

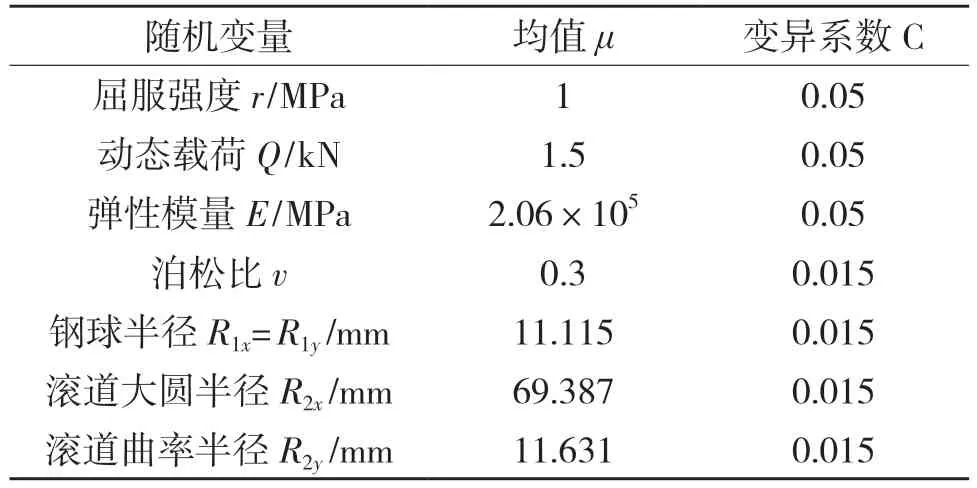
表3 隨機變量參數表Tab.3 Random variable parameters

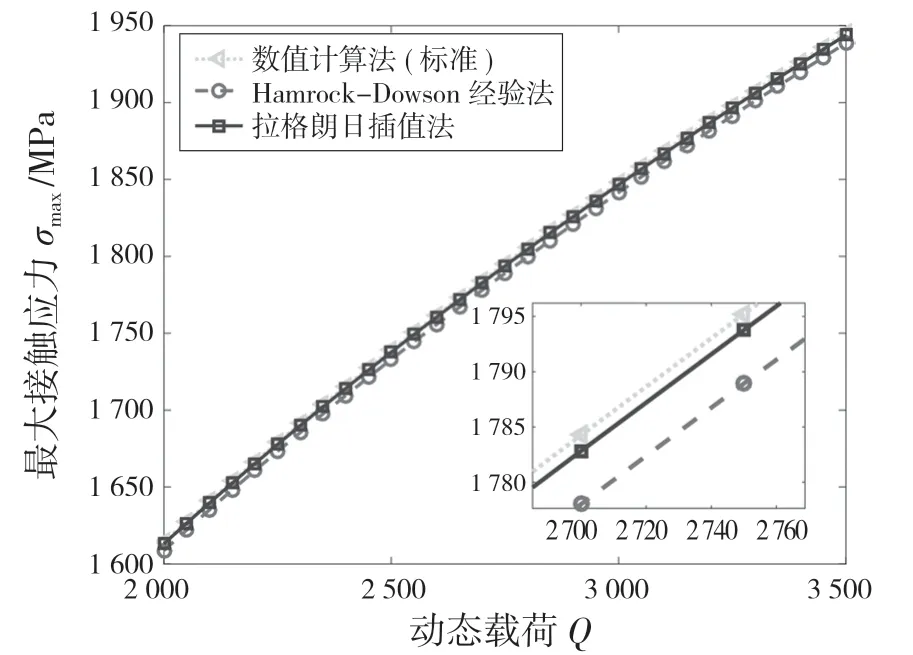
圖4 3 種方法計算的最大接觸應力對比 Fig.4 Comparison of the maximum contact stress calculated by three methods

由圖4 可知，拉格朗日插值法相較Hamrock-Dowson 經驗法更加逼近數值計算法計算的點接觸軸承接觸應力。兩者相對誤差如圖5 所示，2 種方法的相對誤差均小于0.4%，其中拉格朗日插值法的相對誤差小于0.1%。因此，2 種方法均可代替數值計算法用于計算點接觸軸承接觸應力，其中拉格朗日插值法計算結果更加準確。

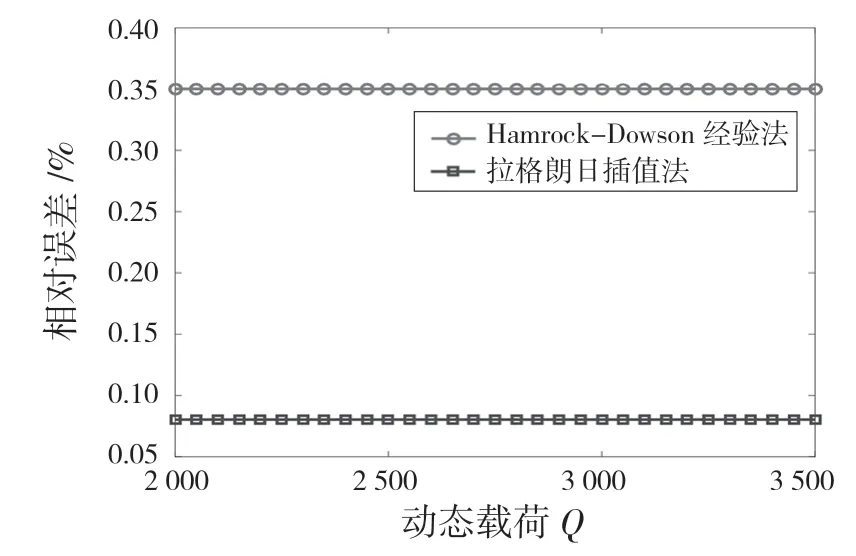
圖5 接觸應力相對誤差Fig.5 Relative error of contact stress

2 動態可靠性分析

由上述分析可知點接觸軸承最大接觸應力呈逼近線性趨勢，因此采用二階矩方法可以滿足其最大接觸應力可靠性及靈敏度分析。

2.1 動態可靠性模型

根據赫茲接觸應力計算理論[3]，點接觸軸承滾動體與滾道的最大接觸應力為

根據應力-強度干涉理論建立機械系統的狀態方程

式中：r——屈服強度；g(X)≤0 時表示結構功能失效。

引入動態可靠性指標β(t)簡化可靠性的分析計算，可靠性指標β(t)的定義為

式中：E[g(X,t)]——狀態函數g(X,t)的平均值；Var[g(X,t)]——狀態函數g(X,t)的方差。

如果基本隨機變量X服從正態分布，則可以計算出結構的可靠度R(t)為

式中：φ(·)——標準正態分布函數。

當強度和所受應力服從正態分布時，采用二階矩法，只需要知道隨機變量的均值和方差，即可計算出系統的可靠度[6]。

不考慮g(X) 2 階以上的部分，取近似的g(X) 2 階均值和1 階方差

式中：Var(X)——隨機變量的方差矩陣。

狀態函數g(X)對隨機變量X的偏導數為

這種求解方式得出的是近似結果，其最大特點是求解過程簡便，具備較強的適應能力，當非線性不是太高時，其求解的精度可以滿足工程實際的要求。

2.2 點接觸軸承動態可靠性分析

根據應力-強度干涉可靠性模型，結合最大接觸應力模型，設動態載荷Q在[0，1]s 內隨時間線性遞增并達到最大值，選取隨機變量X=[r Q E v R1x R1y R2x R2y]。在缺乏充足的實驗數據的前提下，可以通過變異系數C估計隨機設計參數的標準方差[10]，具體見表3。采用該模型作為基于應力-強度干涉理論的狀態方程，可以獲得點接觸軸承的應力-強度可靠性模型。

利用式（22）獲取最大接觸應力隨時間變化的曲線如圖6 所示。由圖6 可知，軸承最大接觸應力在2.69 kN 時超出其屈服強度，根據應力-強度干涉理論建立的動態可靠性模型定義，判定此時的軸承處于失效狀態。

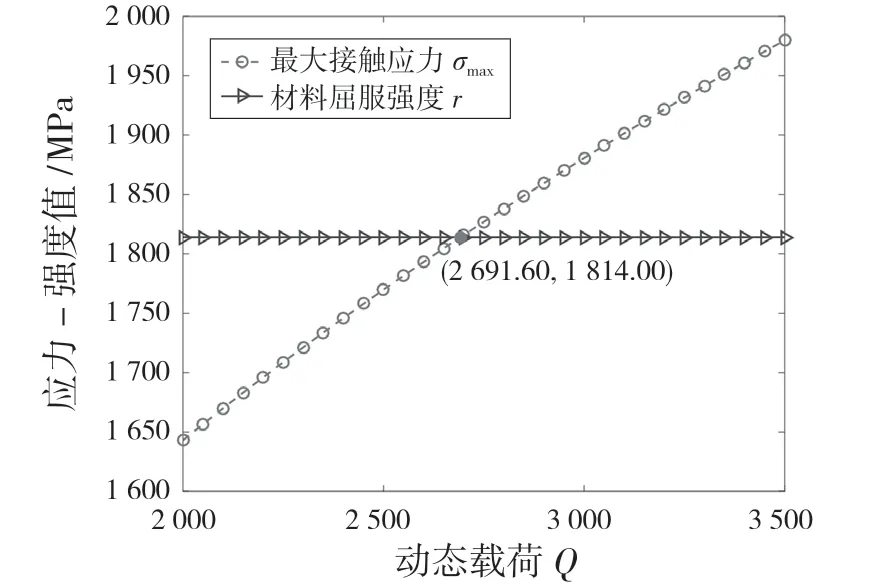
圖6 軸承點接觸應力-強度狀態圖Fig.6 Stress-strength state diagram of point-contact bearing

根據式（24）、式（25）計算動態可靠度，可靠度隨時間變化曲線如圖7 所示。由圖7 可知，軸承的可靠度在22 ms 時出現下降趨勢，說明其在22 ms 時已經出現了早期失效的可能。采用蒙特卡洛法對隨機變量X抽樣后，根據狀態方程計算的基于蒙特卡洛法的可靠度驗證了二階矩法計算的動態可靠度結果的精度。

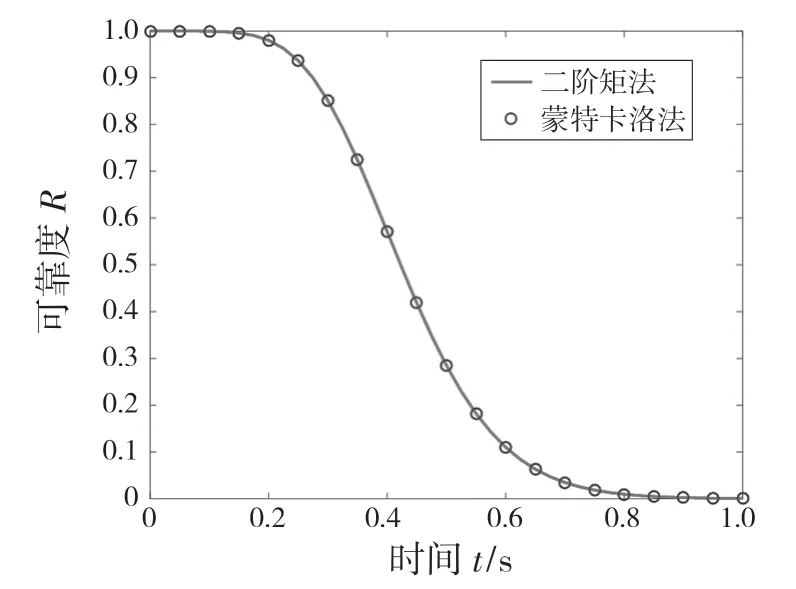
圖7 動態可靠度曲線Fig.7 Dynamic reliability curve

3 動態可靠性靈敏度分析

3.1 動態可靠性靈敏度理論

機械結構可靠性靈敏度分析基于可靠性的敏感度分析，通過計算得出隨機變量對機械結構可靠性的影響，能較好地反映各隨機變量對機械結構的影響[7]。

機械結構的可靠性靈敏度分為對隨機變量X的均值可靠度靈敏度dR(t)/d和方差可靠性靈敏度dR(t)/dVar(X),計算公式分別為

3.2 動態可靠性靈敏度分析

通過式（30）計算均值靈敏度隨時間變化的曲線，如圖8 所示。由圖8 可知，隨機變量鋼球半徑R1x、R1y和滾道曲率半徑R2y對動態可靠性模型的靈敏程度呈正相關趨勢，即增大隨機變量的均值，可提高系統運行的可靠性，反之亦然。在安全域內，各隨機變量靈敏度相差不大；當軸承失效后，軸承材料泊松比ν對系統運行的影響最大，隨機變量鋼球半徑R1x、R1y次之，再次是滾道曲率半徑R2y，而其他隨機變量對系統的影響均可忽略不計。因此在生產制造過程中，通過增大軸承的鋼球半徑R1x、R1y和滾道曲率半徑R2y、減小軸承材料的泊松比ν可以提高機械系統運行的可靠性。

通過式（31）計算軸承方差靈敏度隨時間變化的曲線，如圖9 所示。由圖9 可知，在系統運行完全失效前，增大各隨機變量的標準差會降低系統可靠性；失效后，增大各隨機變量的標準差會提高系統可靠性。因此在設計制造過程中，可通過減小軸承材料泊松比ν的標準差提高系統運行的可靠度。

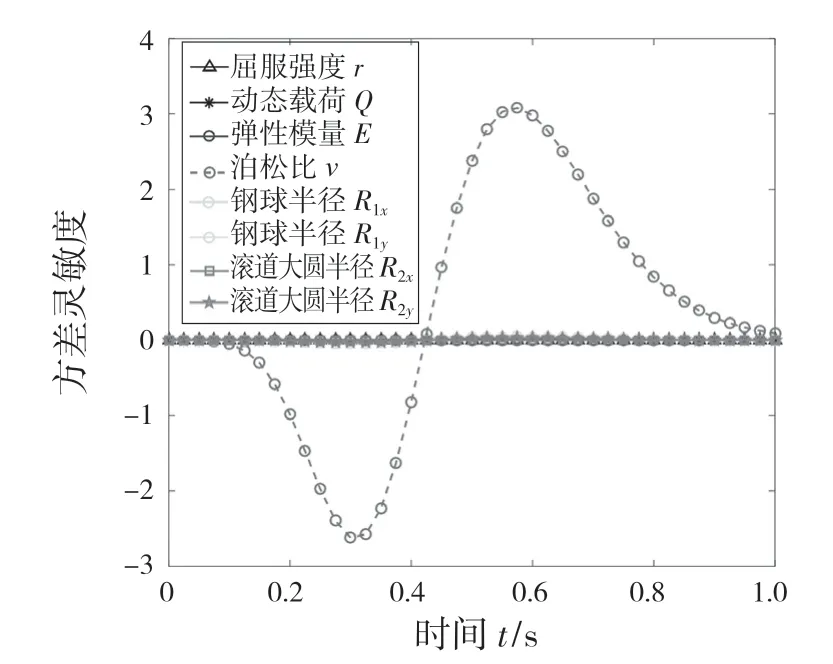
圖9 隨機變量方差靈敏度Fig.9 Sensitivity of variance of random variables

4 結論

（1）基于Hertz 理論研究了點接觸軸承最大接觸應力3 種不同的計算方法：數值計算法、Hamrock-Dowson 經驗法和拉格朗日插值法研究了拉格朗日插值法中3 種計算點接觸的無量綱參數表。結果表明：拉格朗日插值法計算結果更加準確。

（2）根據應力-強度干涉理論建立了點接觸軸承的最大接觸應力動態可靠性模型，采用二階矩法對軸承動態可靠性進行求解，并采用蒙特卡洛法驗證。結果表明：點接觸軸承的可靠度隨動態載荷增加而減小。結合文中算例，軸承承受最大徑向載荷不能高于2.69 kN。

（3）根據可靠性靈敏度分析相關理論，求得點接觸軸承動態可靠性模型中隨機變量對模型的靈敏度。結果表明：增大軸承的鋼球半徑和滾道曲率半徑、減小軸承材料的泊松比及其標準差可以提高機械系統運行的可靠性。