基于深度強化學習的機械臂運動控制研究

王文龍，張帆

（200335 上海市 上海工程技術大學 機械與汽車工程學院）

0 引言

隨著人工智能和機器人技術的發展，機械臂被廣泛應用于工業生產的各個領域，其智能化要求也隨之提高。人工智能和機械臂技術相結合，研究具有自主決策能力的控制方法成為一個重要分支，也是國內外研究的重點和前沿。

機械臂經典控制方法如自適應滑模控制、示教控制、前饋補償控制等，提高了機械臂運動的魯棒性，具有響應速度快、穩定性好和精確度較高等特點。肖任等[1]提出了一種基于時間固定擾動觀測器的滑模控制方法，在消除不確定擾動的基礎上，有效地抑制了系統抖振；Wang 等[2]提出了基于連續軌跡點控制的位置控制方法，提高了機械臂的控制精度。這些控制方法雖有一定成效，仍存在編程難度大、泛化性能弱、適應環境能力較差、智能化程度低等問題。

強化學習（RL）是人工智能的一個重要分支，在深度學習的快速發展下，深度學習和強化學習結合，使強化學習在機器人控制領域有了進一步發展，使其具有強大的感知和決策能力，深度強化學習算法也應用在機械臂的控制領域。尤其是在深度確定性策略梯度（Deep Deterministic Policy Gradient，DDPG）算法[3]被David Silver 等提出后，可以讓深度強化學習算法的經典算法深度Q 學習網絡（Deep Q-learning Network，DQN）拓展到連續動作空間，這使得深度強化學習和機器人技術的結合更加緊密。Peng 等[4]將采用后視經驗重放的方法改進DDPG 算法應用到機械臂，對沖壓自動生產線中的運動物體進行抓取，提高了智能體的樣本的利用，將平均成功率從31%提升到82%；趙寅甫等[5]采用DDPG 算法先2D 后3D 模型的方法，通過數據驅動的訓練過程，控制機械臂到達目標位置，縮短了接近52%的訓練時長；劉勇等[6]將傳統的PID控制方法與DDPG 算法相結合，利用PID 控制快速接近目標位置，采用DDPG 算法使機械臂學習追蹤目標物體投影，并避開障礙物體投影，最終實現在三維空間實現追蹤和避障。

本文使用Gym 官方提供的機械臂深度強化學習訓練環境，重置其獎勵函數，并在DDPG 算法中比較其對機械臂訓練過程的影響，比較不同的深度強化學習算法在機械臂自主學習中的性能。實現虛擬環境中達到較高的獎勵值，并使末端執行器快速、準確地到達目標位置，并保持姿態不變。

1 機器人模型與環境

帶接觸的多關節動力學（Multi-Joint dynamics with Contact,MuJoCo）是一個物理引擎模擬器，主要用于機器人、生物力學、圖形與動畫、機器學習等領域，能夠快速準確模擬鉸鏈結構和環境的交互，它包括廣義坐標系中的多關節動力學、整體約束、干關節摩擦、關節和肌腱極限、無摩擦和摩擦接觸、可能具有的滑動、扭轉和滾動摩擦[7]。本文機械臂模型及其使用的MuJoCo 運行界面如圖1 所示。

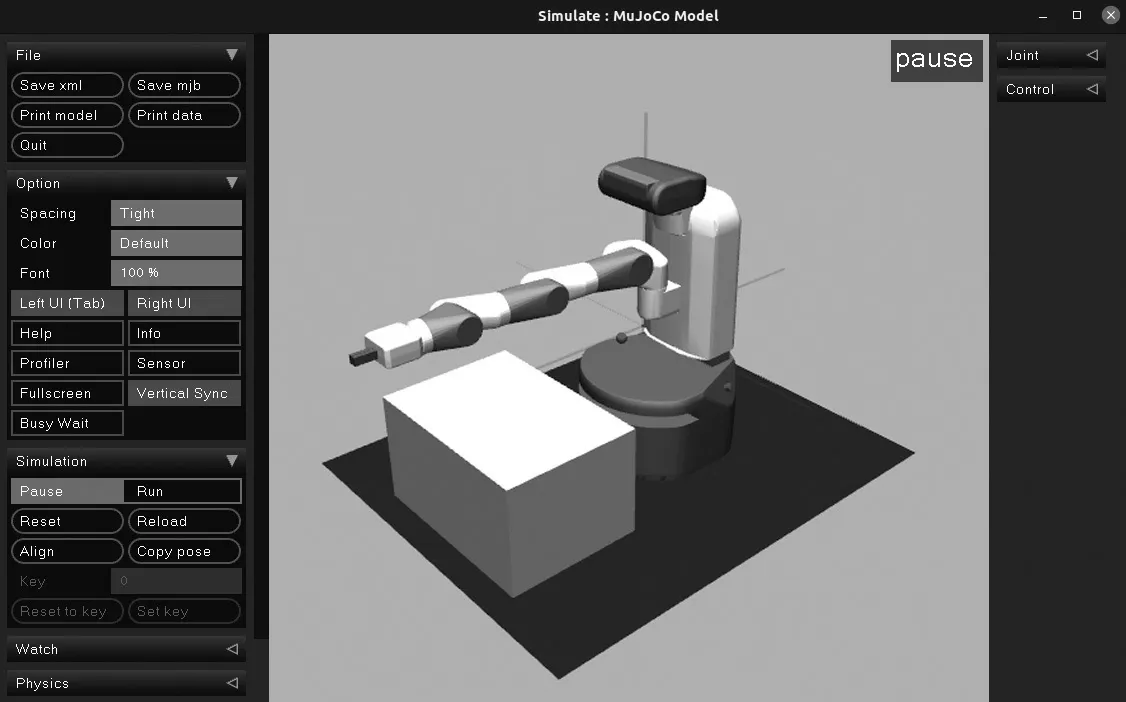
圖1 Simulate 中的機械臂Fig.1 Manipulator in simulate

Gym 是由OpenAI 公司提供的一個可調節參數訓練和比較RL 算法的環境平臺，其中含有很多強化學習環境，包括Atari 游戲、Classic control、MuJoCo、Robotics 等，現在主要支持Python 語言。本文結合Pytorch 框架，進行深度強化學習的訓練。采用的是環境ID 為“FetchReach-v1”的機械臂。在此環境中，主要輸出為當前狀態St、下一時刻的狀態St+1以及輸入動作策略的獎勵值R。狀態包含3 個部分：智能體的觀察狀態、智能體經過動作所到達的位置坐標以及目標位置。狀態作為Actor 網絡的輸入，應為向量形式，在此環境中以字典形式儲存，故需要對此進行預處理，轉化為一維向量。此機械臂的狀態為1×16 的向量。

2 深度強化學習算法

深度強化學習是利用深度學習的感知功能以及強化學習的決策功能的算法，強化學習是在智能體和環境之間交互時，在不被告知采取哪種行動的情況下，智能體通過執行某些動作，基于環境反饋的獎勵或者懲罰不斷地調整其策略、改善其行為、得到最優策略的算法。它包含智能體、環境、獎勵、動作、觀察5 個元素，其交互過程如圖2 所示。

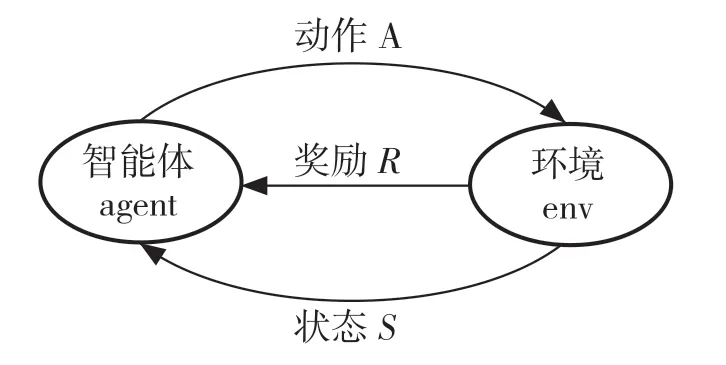
圖2 智能體與環境交互Fig.2 Interaction between an agent and the environment

智能體觀察環境t時刻的狀態S，采取動作A并在環境中執行，得到下一時刻的狀態即St+1，并且獎勵函數對執行的動作A 進行評價，得到獎勵R，反饋給智能體。

2.1 馬爾可夫決策過程

馬爾可夫決策過程（Markov Decision Process,MDP）是深度強化學習的理論基礎，它的4 元素為(S,A(s),R(s,a),P(s,a,s')[8]。其中，S為所有狀態的集合，A(s)為狀態s下的所有動作的集合，R(s,a)為智能體的獎勵值，表示在狀態s下執行動作a后所得到的獎勵值或者懲罰值。P(s,a,s')為狀態轉移概率，在狀態s執行動作a后轉移到狀態的概率值。

在MDP 中有一個較重要的參數為折扣因子γ∈(0,1)，它控制在訓練中一個回合的收益值對下一個動作獎勵值的依賴程度,收益為

執行策略為π時，其狀態分布則為pπ，學習目標為執行最優策略時使期望累計獎勵值達到最大值，累計期望值為

最佳策略可表示為

在尋找最優策略過程中，Bellman 方程給出了最優狀態的值

式中：pa,i→j——在狀態i產生的動作a以狀態j結束的概率。

除了狀態值外，在強化學習中還定義了動作值Qs,a，在Q-learning 中

對于狀態值和動作值的可爾科夫決策過程，進行Bellman 迭代更新

2.2 深度確定性策略梯度算法(DDPG)

DDPG 算法是基于Actor-Critic（演員-評論家）網絡的異策略算法，相比于Actor-Critic 算法，它的策略是確定的，直接根據狀態確定所采取的動作，并且不需要像PG 算法那樣為計算的每個步驟集成到整個動作空間中。這樣可以將鏈規則應用于Q值，通過最大化Q值改進策略。Actor 和Critic 網絡都是3 層神經網絡，其控制策略如圖3 所示。

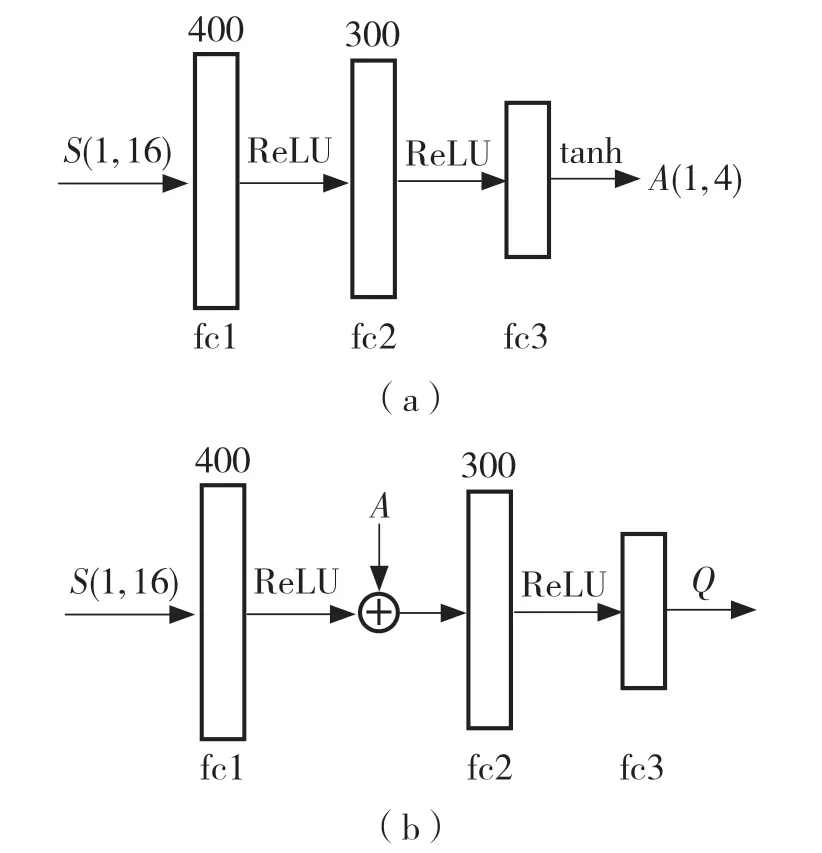
圖3 DDPG 算法的網絡結構Fig.3 Network structure of DDPG algorithm

其中，Actor 網絡是根據每個給定的狀態返回N個值，每個動作一個值，這種映射關系是確定的。Critic 的作用是估計Q值，即在某個狀態下智能體采取的動作經過環境交互所獲得的折扣獎勵。因為動作在網絡中是以數字向量的形式呈現，所以Critic 網絡有2 個輸入，即狀態和動作，動作是在第2 層網絡中輸入，它的輸出是反映Q值的單個數字。Actor 網絡最后一層網絡使用tanh 激活函數主要利用其值域為[-1,1]的特性，保證所得到的動作也是在這個區間內。

DDPG 算法使用了當地（local）和目標（target）2 套神經網絡，在此算法中由于使用的是確定性策略，為了增加機械臂對環境的探索能力，在Actor網絡的返回值中增加噪聲再傳遞給環境來實現，此噪聲被稱為OU 過程，在離散時間情況下可以寫為

式中：θ，μ，σ——超參數。

該式（8）表示OU 過程的下一個值由先前的噪聲值加上一個正常噪聲產生。最終輸入到環境中的動作為

式中：?——超參數，主要作用是動作a對噪聲N的貪婪程度。

DDPG 算法的目標網絡參數更新方式采用軟更新方式，也可稱為指數平均移動，使用超參數學習率，將上一時刻的網絡參數和新的本地網絡參數做加權平均，然后賦給目標網絡

當地的Actor 網絡采用采樣的策略梯度方法進行優化

式中：si——當前時刻智能體觀測到的狀態。

當地的Critic 網絡使用均方差損失函數定義損失，并進行優化更新。在這個過程中使用目標網絡對下一個策略的估計，其預估價值為

式中：ri——當前策略所得到的獎勵值；在本實驗中γ=0.99；Q'——目標Critic 網絡對下一個策略的估值。在此基礎上，其網絡損失函數表示為

3 分布式策略梯度算法

分布式策略梯度算法（D4PG）是由Gabriel Barth-Maron 等在2018 年提出的方法[9]，主要是在DDPG 算法的基礎上進行改進，將經驗收集的Actor 和策略學習learner 分開，使用多個actor 分布式采樣，并儲存在同一個經驗池中，經過優先級重放采樣方式進行采樣[10]，更新后將權重同步到各個actor 上，實現了更好的離線學習。

D4PG算法的Critic網絡使用分布式價值函數，為了引入分布式更新，其隨機變量的返回值為

式中，s=s0，a=a0，a=π(s)。則分布更新的Q為

分布貝爾算子就可以定義為

式中：Jπ——分布貝爾算子，關于隨機變量的概率定律是相等的，此算子雖然跟規范的Bellman 算子相近，但是它所用的函數類型不同。

分布變量采用從狀態到動作對映射到分布的函數，并返回相同形式的函數。為了在此算法中使用這個函數，將其參數化，并定義其損失函數為

式中：d——分布之間的度量，在D4PG 算法中主要使用交叉熵損失來度量。

為了完成這種分布式梯度策略，Actor 網絡的優化方式使對行動價值分布的期望來完成。

在D4PG 中改進的部分還包括在估計TD 誤差時使用N步返回，減少了更新時的方差。

機械臂在D4PG 算法的訓練步驟如下：

（1）超參數輸入：包括學習率、經驗池大小、批量大小、經驗池初始大小、軌跡長度等；

（2）環境激活：定義網絡、智能體、經驗池，隨機初始化網絡的權重(θ,ω)，初始化目標權重(θ',ω')，定義Actor 和Critic 網絡參數優化器；

（3）進行400 000 次循環訓練；

（4）為更好地探索環境，初始化隨機過程噪聲；

（5）初始化環境，獲得觀察狀態s；

（6）對觀察狀態進行預處理；

（7）經過100 次隨機動作熱身后，將經過處理的狀態輸入Actor 網絡返回π(s)；

（8）對π(s)增加隨機噪聲得到動作，并返回環境，得到獎勵值及下一個狀態值s'，并將(s,a,r,s')儲存在經驗池中；

（9）當循環次數大于經驗池初始大小值時對經驗池進行優先級重放的方式采樣；

（10）構建目標分布：

(11)計算Actor 和Critic 網絡進行更新參數：

(12)更新網絡參數：

(13)采用軟更新方式對目標網絡更新：

(14)每1 000 次對訓練模型進行測試，并保存最好模型。

4 仿真實驗與結果

4.1 重置獎勵函數

在Gym 環境中設置的獎勵值為稀疏獎勵，其獎勵函數為

式中：δ——機械臂到達目標位置的精度，在此環境中設定為δ=0.05。

在訓練初期，使用此獎勵函數訓練速度慢，效果不顯著，主要原因是探索環境中不同的動作策略可能出現相同的獎勵值，導致機械臂學習速度較慢。考慮到稀疏獎勵訓練困難，使用線性獎勵函數

設置此獎勵函數的原因為：在環境訓練中，包含有正負獎勵值的獎懲方式對機械臂訓練穩定有較好的幫助，先利用DDPG 算法進行訓練并與獎勵函數r=-d（全負獎勵）進行比較，其訓練結果經過0.6因子的平滑后如圖4，圖5 所示。在訓練過程中的測試獎勵如圖6 所示。

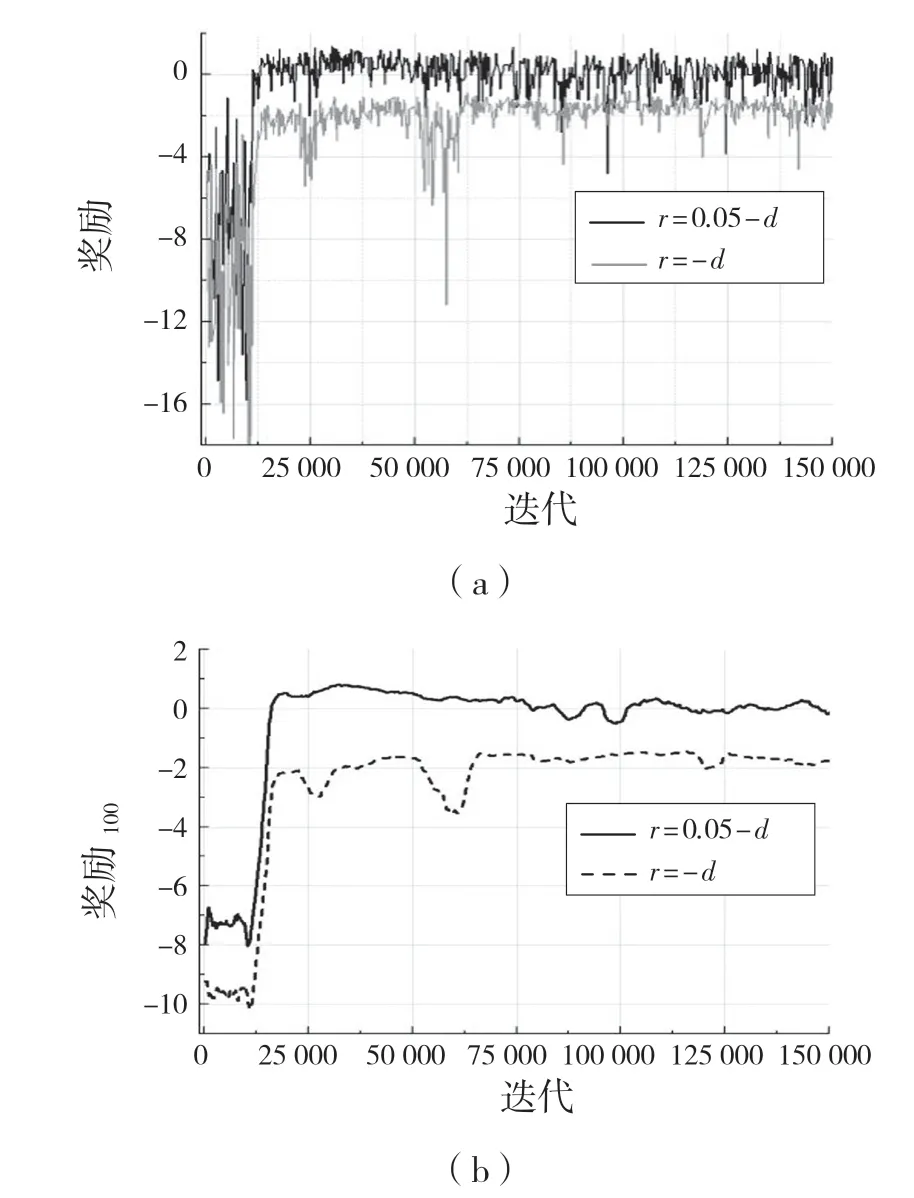
圖4 DDPG 算法下訓練期間的獎勵Fig.4 Rewards during training under DDPG algorithm

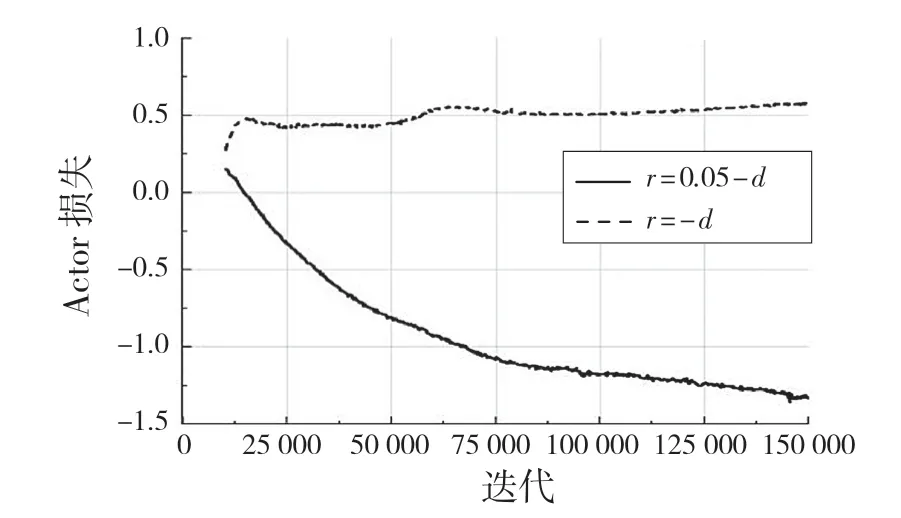
圖5 DDPG 算法下Actor 網絡損失Fig.5 Actor network loss under DDPG algorithm

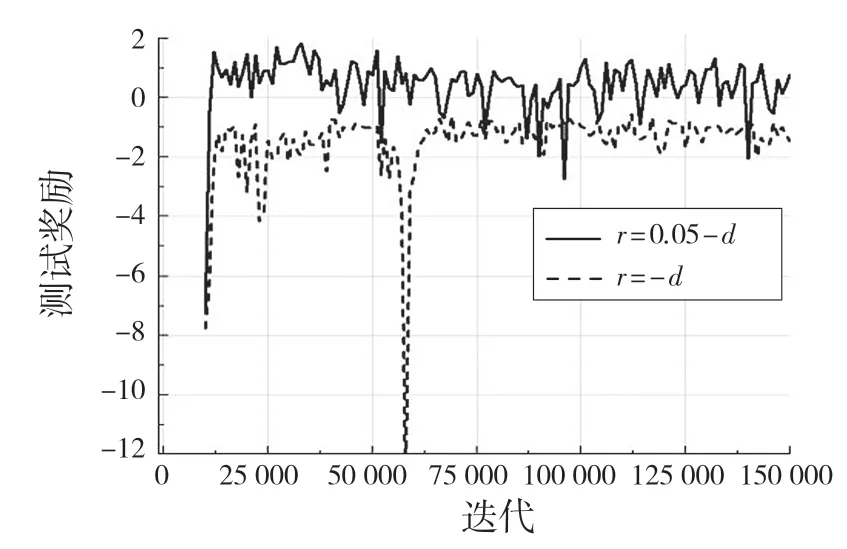
圖6 不同獎勵函數的測試結果Fig.6 Test results of different reward functions

在對DDPG 算法的2 種獎勵機制訓練得到的最好模型進行100 次可視化實驗，均能在精度范圍內到達指定位置，但是獎勵函數為r=-d的模型在到達指定位置后出現幅度較大的抖動現象，而r=δ-d的獎勵機制所訓練的最好的模型在100 次實驗中未出現抖動現象。

通過實驗可以看出，帶有正負樣本的獎勵機制對機械臂訓練穩定性有顯著的作用，其每個策略的獎勵值在達到較好的獎勵值后不會出現大幅度的下降，Actor 網絡和Critic 網絡的損失函數收斂較為穩定，不會出現激增現象。

4.2 D4PG 訓練參數設定

在D4PG 訓練過程中有很多關鍵超參數，對訓練結果至關重要，如果參數不合理，可能造成訓練不穩定，達不到預期要求。本實驗的超參數設定如表1 所示。

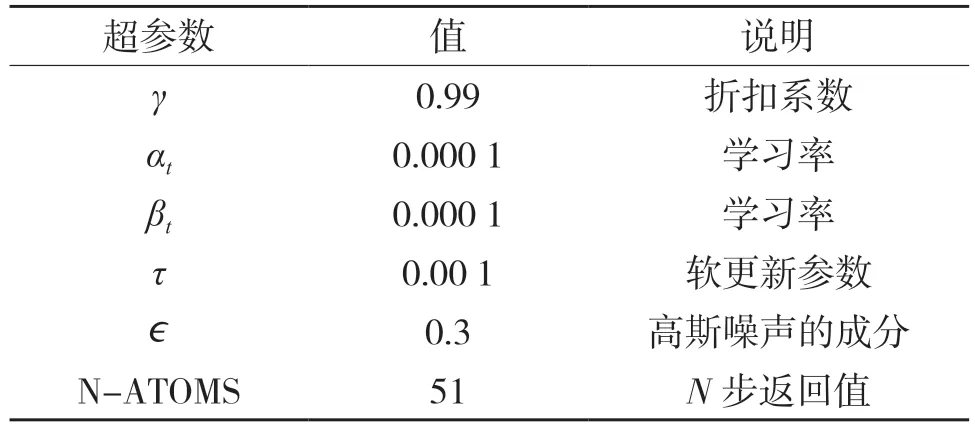
表1 D4PG 算法的超參數設定Tab.1 Hyperparameter setting of D4PG algorithm

4.3 D4PG 訓練結果及分析

結合上述較佳獎勵機制，設置隨機目標位置，利用D4PG 算法對機械臂進行訓練，每次100 個回合，每回合50 步，進行400 k 次訓練，并相應地用DDPG 算法訓練，結果如圖7、圖8 所示。

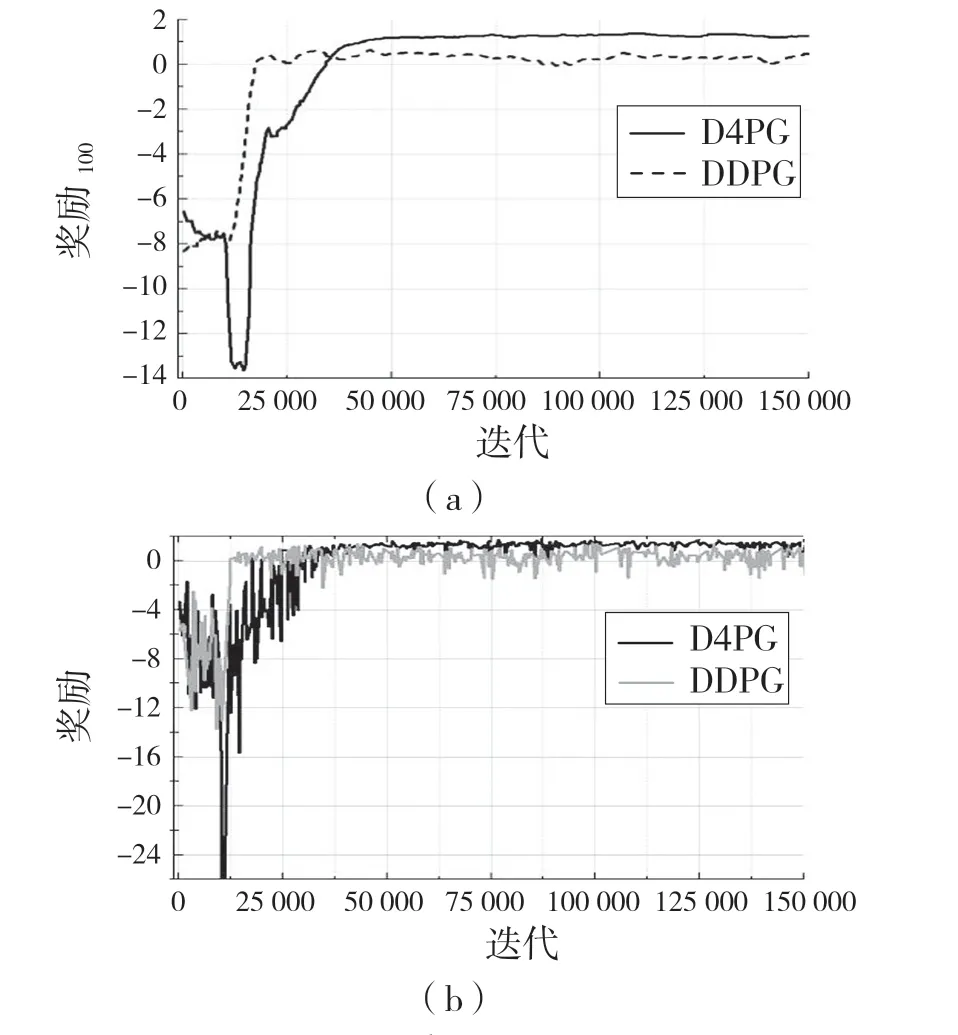
圖7 機械臂訓練期間獎勵Fig.7 Rewards during manipulator training

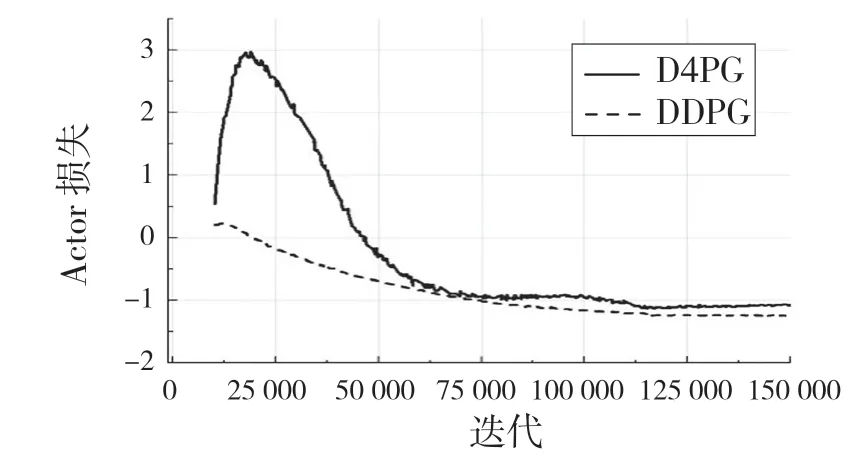
圖8 機械臂訓練期間損失Fig.8 Loss of manipulator during training

圖7 為機械臂在訓練期間的獎勵變化曲線，其中圖7（a）為每100 個回合平均獎勵值，圖7（b）為每幀的獎勵值。從圖7 可以看出，D4PG 算法在訓練中能收斂到更好的獎勵值，接近環境的最高獎勵值；DDPG 算法在前期獎勵值大于D4PG，這主要原因是D4PG 是先采樣一定數量的動作后再進行智能體的學習過程。

從圖8 的Actor 和Critic 網絡的2 種算法的損失對比，D4PG算法的性能更優，訓練過程更加穩定，收斂度好。在訓練過程中每1 000 次對訓練模型進行測試，測試結果如圖9 所示。

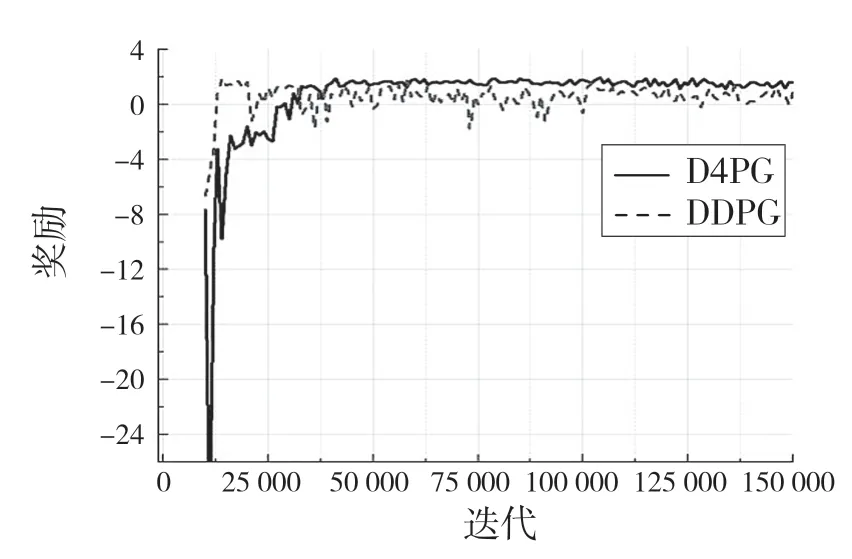
圖9 機械臂測試期間獎勵Fig.9 Rewards during manipulator testing

在測試中可以看出D4PG 訓練的模型在測試中比DDPG 算法表現更好，能更快接近環境的最大獎勵值，并保持較穩定的收斂狀態，而DDPG 收斂到最大獎勵值的速度慢。在經過400 k 幀的訓練中，D4PG 算法最大達到了1.978 的獎勵，已經非常接近環境的最大獎勵值了。

5 結論

控制策略對機械臂生產效率有很大影響，好的控制策略能起到事半功倍的效果。本文利用DDPG算法，研究獎勵函數對機械臂訓練的作用。利用較好的獎勵機制，使用D4PG 算法進行機械臂末端執行器到達目標位置進行仿真訓練，相比于DDPG 算法，D4PG 訓練過程更加穩定，在最短時間內收斂，在相同次數的測試中能達到更大的獎勵。模型可視化實驗中也能以100%的成功率到達目標位置。利用深度強化學習控制策略使機械臂的控制更加智能化，效率更高。

在D4PG 算法的模型測試中也遇到了一些問題，最好的測試模型在可視化實驗中會出現到達目標位置后發生抖動現象，但是在測試中獎勵值次一點的模型可視化實驗中未出現抖動現象，需要進一步研究和改進。