焊接機器人齒輪齒條機構疲勞壽命仿真分析

劉鵬飛，曹陽，陳國雄

（1.550025 貴州省 貴陽市 貴州大學 機械工程學院；2.550081 貴州省 貴陽市 貴陽萬江航空機電有限公司；3.550025 貴州省 貴陽市 貴州省機電裝備工程技術研究中心）

0 引言

齒輪齒條傳動機構是一對將旋轉運動轉化為直線運動的裝置，作為焊接機器人關鍵傳動部件，具有承載能力大、傳動精度高和運行平穩等優點。由于齒輪齒條上輪齒接觸面長期處于周期性交變接觸力的作用下，容易導致輪齒表面損傷或輪齒斷裂等問題，使其傳動失穩，甚至失效[1]，進而影響焊接機器人的焊接工作，因此，有必要對焊接機器人齒輪齒條傳動機構進行結構強度研究。劉本學等[2]以齒根拉應力仿真結果作為有限元疲勞分析的數據來源，利用SolidWorks 與ANSYS Workbench/ Fatigue Tool 對直齒圓柱齒輪進行彎曲疲勞仿真分析，再將結果與疲勞試驗數據進行對比，從而驗證仿真結果的可靠性；張延杰等[3]利用ANSYS 與ADAMS 軟件建立斜齒輪副的柔體動力學模型，提取到了斜齒輪副的虛擬載荷譜，結合斜齒輪副5 齒對有限元模型的靜態接觸分析結果，利用nCode 疲勞分析軟件研究了齒廓偏差對斜齒輪副疲勞壽命的影響規律；嚴宏志等[4]應用修正的局部應力應變法分析了不同齒面粗糙度下面齒輪的疲勞裂紋生成壽命，再結合損傷容限設計法預測了面齒輪的裂紋擴展壽命。目前，對不同載荷、齒間摩擦系數和齒輪轉速對齒輪齒條疲勞壽命影響的研究還比較少見。

本文以自行研制的焊接機器人龍門架組件上的齒輪齒條傳動機構作為研究對象，利用三維設計軟件建立齒輪齒條的參數化模型，并導入有限元軟件建立其瞬態動力學模型，通過仿真獲得齒輪齒條傳動機構的有限元結果，結合疲勞損傷理論，分別研究不同載荷、齒間摩擦系數和齒輪轉速對齒輪齒條疲勞壽命的影響，為齒輪齒條在動態條件下的抗疲勞優化提供理論指導。

1 齒輪齒條有限元建模

1.1 參數化建模

齒輪齒條傳動機構主要功能是將動力傳給齒輪，并將齒輪回轉運動轉變為齒條往復直線運動，使龍門架組件在Y向上往復直線運動。本文選擇較易加工的直齒式齒輪齒條。為達到焊接機器人設計所需的性能要求，初步選定齒輪齒條的材料屬性為：材料42CrMo，密度7 850 kg/m3，彈性模量2.12×1011Pa，泊松比0.28，屈服極限σs=930 MPa，抗拉強度σb=1 080 MPa。在最大運行速度條件下，初步計算其齒輪齒條傳動機構的設計參數，齒輪齒條模數2 mm，齒輪齒數23，齒輪齒寬25 mm，壓力角α=20 °，齒輪軸徑22 mm。通過SolidWorks 建立直齒式齒輪齒條的三維實體模型。具體的齒輪齒條傳動機構裝配體模型如圖1 所示。

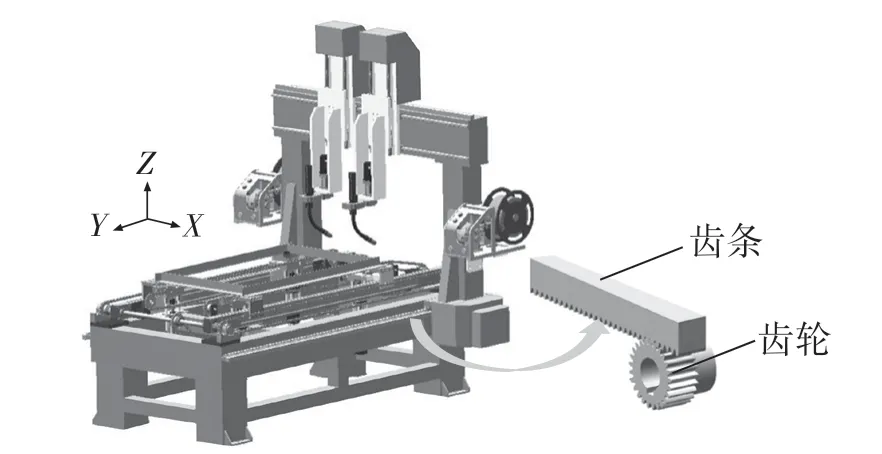
圖1 齒輪齒條傳動機構裝配體模型Fig.1 Assembly model of rack and pinion transmission mechanism

1.2 簡化有限元模型

為提高求解效率，在保障仿真精度可靠的前提下，可適當簡化齒輪齒條模型結構。由于設計的齒輪為標準直齒圓柱齒輪，計算可知其與齒條嚙合時齒輪副的重合度約為1.981。因此，模型簡化時須保留2 對齒輪處于嚙合狀態，即保證同一時刻齒對嚙合達到重合度要求。簡化后的齒輪齒條傳動機構模型如圖2 所示。

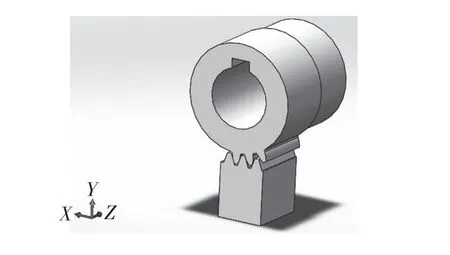
圖2 齒輪齒條傳動機構簡化模型Fig.2 Simplified model of rack and pinion transmission mechanism

進行瞬態動力學有限元分析時，模型網格劃分質量直接影響仿真結果的準確性，因此，有必要確保網格質量在0.6 以上。由于齒輪面的動態接觸轉動屬于非線性接觸分析，所以可采用多區域劃分法。將網格大小設為0.5 mm，采用剛度矩陣較為稀疏的四面體（Tetrahedrons-element）單元對齒輪齒條模型進行有限元網格劃分。

2 齒輪齒條瞬態動力學分析

2.1 邊界條件確定

本文齒輪齒條傳動機構的約束邊界條件為：齒條固定于機架上，而齒輪則在齒條上做圓周滾動。輪齒間的齒面接觸類型設為有摩擦類型，并給定齒間的摩擦系數為0.15。采用閉環步進電機作為動力，其最大轉速為2 000 r/min；減速器的傳動比為1∶10，可計算出齒輪的最大轉速為200 r/min，在最大線速度條件下齒輪轉速為2.65 rad/s。

由于運行過程中齒輪受到的負載主要來自龍門架組件的重力和直線導軌間產生的摩擦阻力，所以可在齒輪轉動方向的反向施加一個水平力來模擬上述負載[5]。本文研究的焊接機器人龍門架組件的總質量為365 kg，即負載力為3 650 N。考慮到輪齒間存在間隙，在啟動運行階段比較容易產生較大的沖擊載荷，需要考慮靜態安全系數fs的影響，故在齒輪鉸接處施加的負載f為

式中：f——龍門組件產生的阻力；FN——龍門組件重載荷；K——直線導軌摩擦系數，取K=0.15。

靜態安全系數fs=8，經計算，傳動裝置與軌道之間的最大摩擦力為2 190 N。

最終，在ANSYS Workbench Transient Structural仿真環境中添加相應的約束、接觸和載荷等邊界條件，得到齒輪齒條傳動機構的瞬態動力學，如圖3所示。

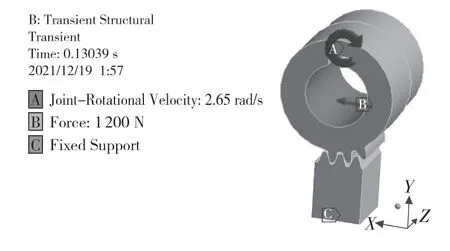
圖3 齒輪齒條傳動機構的瞬態動力學Fig.3 Transient dynamics of rack and pinion transmission mechanism

2.2 瞬態動力學求解與分析

齒輪齒條在瞬態嚙合過程中，2 個零部件處于接觸狀態，受力最大處易產生接觸穿透和膠合現象，造成強烈磨損[6]。因此，對齒輪齒條嚙合過程的接觸穿透分析是判斷其是否會發生膠合現象。

本文采用時間積分算法對齒輪齒條傳動機構的瞬態動力學模型進行求解。根據齒輪的恒值轉速計算出其運轉周期約為2.37 s。為了保證2 個輪齒形成完整的嚙合過程，對瞬態動力學模型的求解時間設為0.206 s。設置初始子步為50，最小子步為10，最大子步為100。經求解后，得到齒輪齒條傳動機構的接觸穿透云圖如圖4 所示。

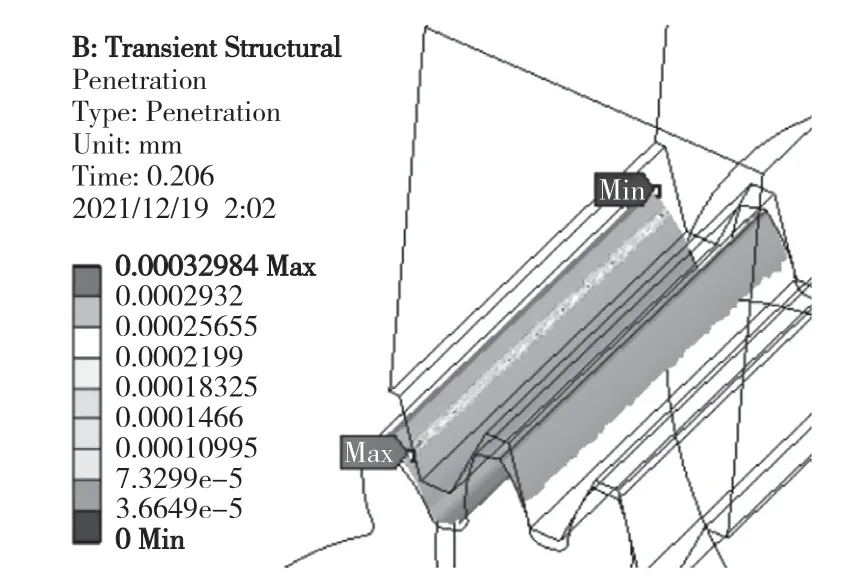
圖4 齒輪齒條傳動機構接觸穿透云圖Fig.4 Contact penetration cloud diagram of rack and pinion transmission mechanism

由圖4 可知，最大穿透量發生在齒輪分度圓處，最大值為3.298 4×10-4mm。齒輪齒條的總體穿透量極小，可近似看作無穿透，說明該齒輪齒條傳動機構工作時不會發生膠合現象。

為了分析齒輪齒條傳動機構在運行過程中是否具有足夠的強度，通過ANSYS Workbench 后處理分別提取齒輪齒條嚙合過程中產生的接觸應力與最大節點應力時間歷程曲線進行分析，如圖5 所示。

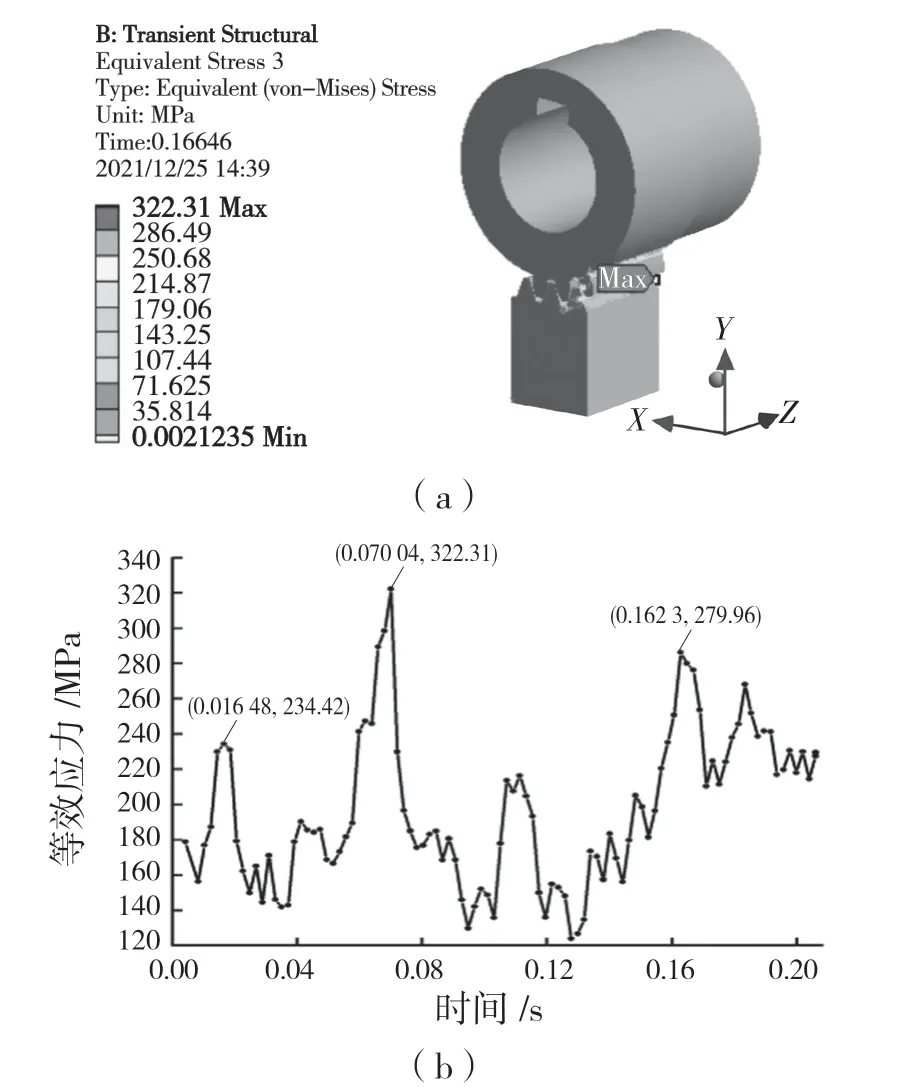
圖5 齒輪齒條嚙合接觸應力及應力時間歷程曲線Fig.5 Meshing contact stress and stress time history curve of rack and pinion

從圖5（a）明顯看出，齒輪齒條傳動機構的最大接觸應力發生在齒間嚙合區域和齒根位置處，這與現實相符。從圖5（b）可知，在0～0.051 5 s 啟動階段，齒輪齒條傳動機構出現了較大的沖擊現象，并在0.016 48 s 時其接觸應力達到234.42 MPa，隨后就逐漸進入平穩嚙合狀態；在0.022 66～0.206 s穩定運行階段，接觸應力隨時間的變化而呈現周期性“峰波”變化，并在0.070 04、0.162 30 s 時，由于齒輪與齒條的接觸面之間發生接觸碰撞分別產生322.31、279.96 MPa 的較大接觸應力。由上述分析可知，齒輪與齒條嚙合過程中產生的接觸應力均小于材料的屈服強度930 MPa，說明齒輪齒條傳動機構滿足強度設計要求，所以當其發生失效時，屬于典型高周疲勞破壞，可采用名義應力法對齒輪齒條進行疲勞計算。

3 齒輪齒條疲勞分析

3.1 疲勞損傷理論

由于長期受交變耦合接觸應力的作用，齒輪與齒條上輪齒比較容易發生表面損傷和疲勞破壞等失效，嚴重可能會導致整個齒輪斷裂，從而出現傳動失效。工程上常用的累積損傷計算有以下2 種：

（1）Miner 線性累積損傷理論

工程上常用的累積損傷計算大多基于Miner 理論，認為材料在不同應力值下造成的損傷是獨立存在的，在循環載荷的作用下，材料受到的損傷逐步線性疊加，直到發生疲勞破壞。即材料在某一橫幅循環應力σi作用下的疲勞壽命為Ni，則得到ni次循環載荷下的損傷率為[7]

根據Palmgren-Miner 線性損傷累積理論計算不同水平的載荷循環對構件的損傷，當材料在K個應力水平Di的作用下經受ni次循環后，其受到的總損傷值為

式中：D——總損傷值；ni——構件在第i級應力幅值；Ni——構件在第i級應力幅值。

（2）非線性疲勞累積損傷理論

非線性疲勞累積損傷理論最典型的是Carten-Dolan 理論，認為前一次載荷造成的損傷會對后一次載荷造成的損傷產生影響[8]。

①一次循環后對結構材料造成的疲勞損傷為

式中：m——結構損傷核的數量；r——損傷擴展速率；c，d——結構材料常數。

②2n個循環對材料造成的損傷為

等副加載條件：

變副加載條件：

式中：p——水平載荷作用下的載荷數。

③臨界疲勞損傷為

在變載荷中，“1”是已作用的載荷中壽命值最大一級；在等副載荷中，N1是疲勞壽命值，則

因疲勞損傷核產生后不會在后面的疲勞加載過程中消失，只會增加，則mi=m1，其中m1=max（mi），式（8）變化為

因損傷發展速率r正比于應力水平S，則有

式中：S1——循環載荷中最大一次載荷；N1——對應的疲勞壽命。

3.2 疲勞分析框架搭建

本文采用疲勞分析法對齒輪齒條傳動機構進行疲勞壽命預測。采用Workbench Transient Structural做齒輪齒條傳動機構瞬態動力學分析時，由于可直接獲得齒輪齒條上隨時間變化的應力時間歷程，所以在nCode 軟件中無需設置載荷譜類型即可進行疲勞分析。該疲勞分析方法先將有限元結果進行轉化，獲得應力張量時間歷程，再把應力張量轉化為應力標量，然后再進行循環計數，得到應力幅值、應力均值與循環次數的關系，最后根據應力計數結果并結合材料的S-N曲線進行疲勞壽命分析，其轉換形式為[9]

式中：SE——綜合應力影響因素；Sm——應力集中系數；St——載荷放大系數；Om——殘余應力水平；Ot——偏移值；δ——有限元分析結果；D——應力張量縮放系數；Pk（t）——載荷時間歷程。

在nCode SN TimeSeries（DesignLife）模塊中搭建動載條件下的疲勞分析框架，如圖6 所示。

圖6 動載條件下的疲勞分析框架Fig.6 Fatigue analysis framework under dynamic load

由于nCode 疲勞分析軟件的材料庫未含有本文齒輪齒條使用的材料（42CrMo），需在Material Map 中創建相應的材料。考慮UTS 修正后，擬合得到材料42CrMo 的S-N曲線，如圖7 所示。設置Goodman 方法對載荷譜進行平均應力修正。求解齒輪齒條的疲勞壽命云圖，如圖8 所示。

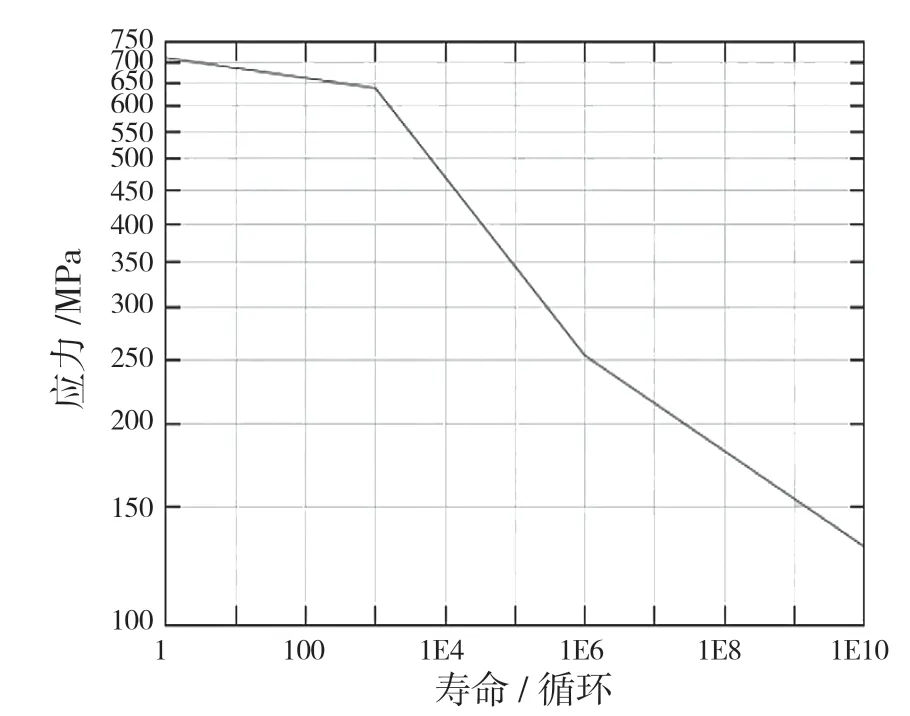
圖7 修正后42CrMo 材料的S-N 曲線Fig.7 S-N curve of 42CrMo material after correction

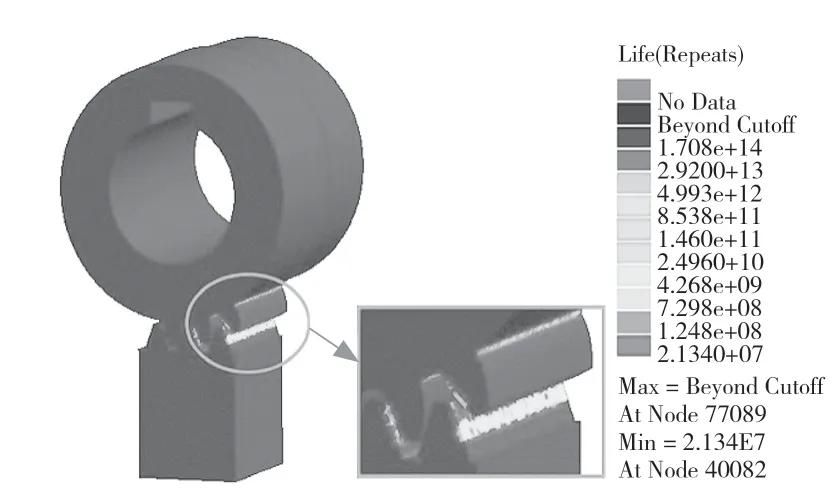
圖8 動載荷條件下齒輪齒條的疲勞壽命云圖Fig.8 Fatigue life cloud diagram of rack and pinion under dynamic load

由圖8 可知，在動載條件下，在節點40 082 處，該位置的最小疲勞壽命值為2.134E+07。進一步分析可知，圖8 中橢圓框選區域為齒輪齒條接觸面，由于在嚙合區域產生齒面相對滑移時間較長，且在該過程中產生的集中應力較大，因而在該區域容易發生疲勞損傷，造成疲勞失效。

由圖9 可明顯看出，在靠近分度圓附近區域，存在許多灰色點狀，表明該位置疲勞損傷最為嚴重，最大疲勞損傷值為4.687×10-8，遠小于1。綜合上述分析，可通過熱處理工藝改善齒面的滲透厚度降低齒面摩擦系數以及減少應力集中，有效延長齒輪齒條使用壽命。

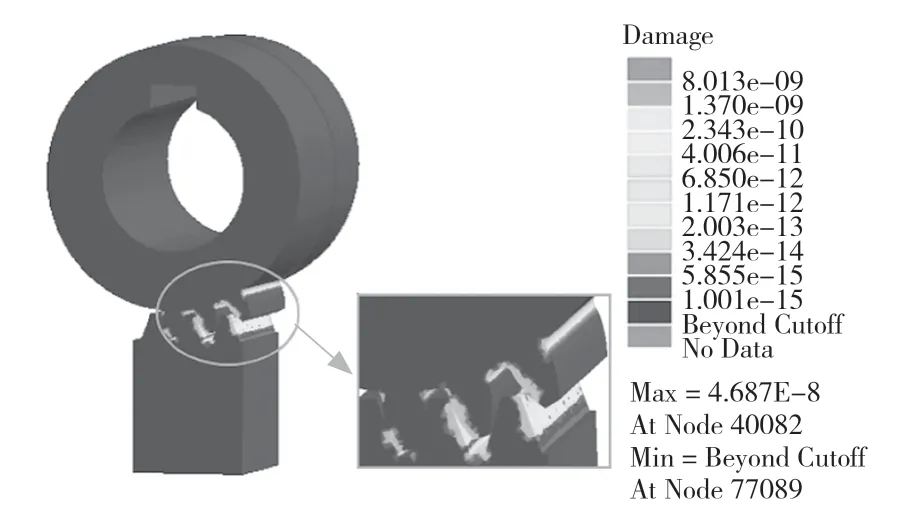
圖9 動載荷條件下齒輪齒條的疲勞損傷云圖Fig.9 Fatigue damage cloud diagram of rack and pinion under dynamic load

3.3 不同輸入參數對齒輪齒條疲勞的影響

齒輪與齒條嚙合，齒間嚙合時的摩擦系數、齒輪輸入轉速及負載嚴重影響齒輪齒條的疲勞特性。齒間接觸面的摩擦系數越大，產生的接觸應力越大，造成接觸面的磨損也越嚴重[10]；齒輪的輸入轉速影響齒間嚙合頻率，輸入轉速值越大，輪齒間接觸面接觸的時間越小，產生的接觸應力越大；負載是齒輪齒條嚙合過程中的阻力，負載值越大，運動阻力越大，嚙合時齒面接觸力越大，產生疲勞破壞的可能性就會增加。

為研究接觸摩擦系數、齒輪轉速、負載對齒輪齒條動態特性的影響，設定摩擦系數為0.1、0.2、0.4、0.6、0.8，轉速為1.5、2.0、2.5、3.0、3.5 rad/s，負載為1 000、1 500、2 000、2 500、3 000 N，研究齒輪齒條嚙合過程中的動態特性，結果如圖10所示。由圖10（a）可見，當齒間摩擦系數增大時，齒輪與齒條受到的等效應力逐漸增大，當摩擦系數為0.1～0.4μm 時，等效應變化較為緩慢，增加率約為33.8 MPa；摩擦系數為0.4～0.8μm 時，齒間產生的等效應力呈線性增加，增加率近149.6 MPa。不同轉速對齒間產生的等效應力也不同，低轉速下齒間嚙合產生的等效應力變化不大，在較高轉速運行條件下，產生的疲勞等效應力增加較為明顯。

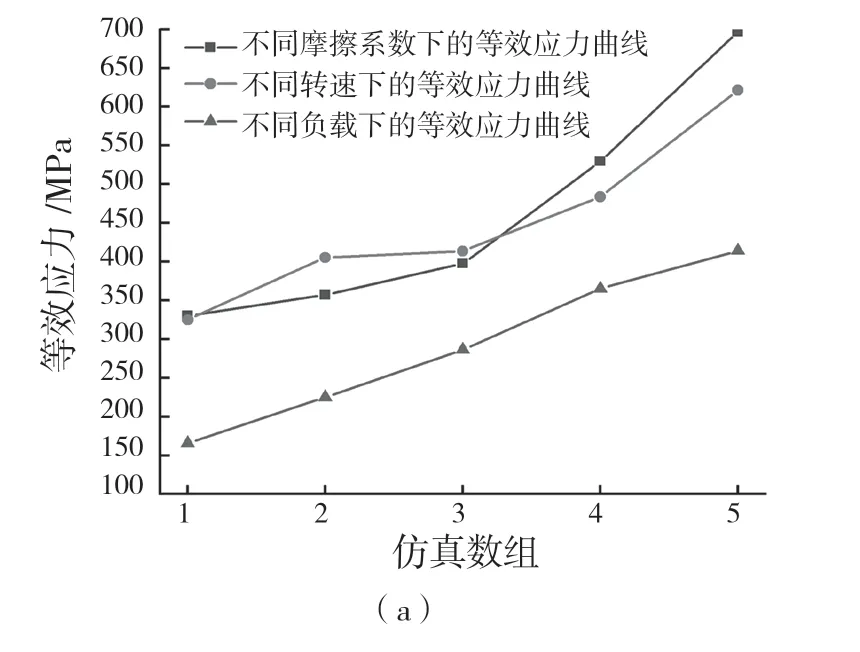
圖10 不同輸入條件下的齒輪齒條嚙合性能Fig.10 Meshing performance of rack and pinion under different input conditions

由圖10（a）明顯看出，隨著負載的增加，齒間產生的等效應力增加呈線性變化，負載每增加500 N，等效應力增加近62.11 MPa。由圖10（b）可見，齒輪轉速對齒輪齒條產生疲勞循環次數的影響最明顯，負載和摩擦系數的影響較小，在輸入參數為0.8μm、3.5 rad/s、3 000 N 時，對應的疲勞循環次數分別為1.31E+04、2.85E+05、2.29E+06 次。由圖10（c）可知，低輸入參數值對齒輪齒條產生的疲勞損傷值較小，當輸入參數值逐漸增加時，產生的疲勞損傷逐漸增加，在摩擦系數為0.8μm 時，最大疲勞損傷值為6.86×10-6，這是由于齒輪齒條嚙合表面的粗糙度越大，嚙合時造成的磨損越嚴重，轉速對齒輪齒條疲勞損傷的影響程度次之，最小為負載。

綜上分析可知，為提高齒輪齒條的動態特性，增加其使用壽命，在滿足疲勞設計時，可對齒輪表面進行處理，降低摩擦系數，同時降低齒輪轉速以及減少負載，可有效提高齒輪齒條的動態性能。

4 結論

（1）利用有限元分析軟件對齒輪齒條傳動機構進行瞬態動力學分析，當處于平穩運行時，齒輪齒條接觸嚙合時產生的最大等效應力值均小于其材料屈服應力，滿足強度設計要求。

（2）齒輪齒條在動載荷下，接觸應力最大值位于齒面分度圓的過渡區域，該區域齒面接觸時產生的相對滑移時間最長，應力較為集中，此區域產生的疲勞損傷最嚴重。

（3）通過ANSYS 與nCode 聯合疲勞仿真分析，得出在動載荷條件下，摩擦系數對齒輪齒條產生最大等效應力影響較大，轉速變化對疲勞循環的影響較為明顯。