基于新型趨近律的PMSM 模糊自適應積分滑模控制

李虎，劉泓濱

（650500 云南省 昆明市 昆明理工大學 機電工程學院）

0 引言

近年來，永磁同步電機（PMSM）憑借結構簡單、輸出效率高和散熱快等優勢被廣泛應用于數控機床、航空航天以及機器人等領域。但由于PMSM是一種多變量和強耦合的非線性復雜系統，當電機受到負載干擾或參數發生改變時，系統性能無法得到有效保證。因此，所設計的各種控制器必須具有很好的穩定性以及抗負載能力。目前，常用的PMSM 調速控制策略主要有PI 控制、自適應控制、滑模變結構控制以及其他的智能控制算法。甘志涵等[1]采用傳統的PI 控制算法對PMSM 進行調速，雖然PI 控制器結構簡單、便于實現，但是這種控制方法很容易受到外部干擾和電機參數變化的影響，很難得到理想的控制結果；任金霞等[2]研究了模型參考自適應控制在PMSM 中的應用，當電機負載發生突變時，模型參考自適應控制效果不理想；樊英杰等[3]采用模糊PI 控制算法對PMSM 的矢量系統進行優化，由于模糊推理規則庫是由專家經驗規定的，所以模糊PI 控制也難以達到預期效果；張蘇英等[4]基于趨近律設計了滑模變結構控制算法，這種控制算法受外界干擾以及電機參數變化的影響較小，所以具有較好的魯棒性，但在電機控制過程中存在抖振現象，因此削弱抖振是滑模控制中需要解決的首要問題。為了克服滑模控制存在的抖振和控制精度不高的問題，很多學者進行了深入研究，并取得了大量成果。王要強等[5]、閆宏亮等[6]、郭小定等[7]對傳統趨近律進行了改進，研究結果表明,新型趨近律可有效削弱系統的抖振并提高系統收斂速度。張攀等[8]結合新型趨近律設計了一種滑模控制器，在控制器中引入雙曲正切函數，改善了系統抖振。

總結上述經驗，本文將模糊控制和積分滑模控制相結合，設計了一種具有積分滑模面和參數自適應的滑模變結構控制器。為了研究該控制器在PMSM 速度調節系統中的控制效果，在MATLAB/Simulink 中搭建PMSM 調速系統的仿真模型并進行仿真分析，比較分析模糊自適應積分滑模控制系統與指數趨近率的滑模控制和PI 控制系統在電機負載時轉速、三相電流以及電機電磁轉矩的變化。

1 PMSM 的數學模型

PMSM在同步旋轉坐標系d-q下的電壓方程[9]為

電機磁鏈方程為

將式（2）代入式（1）得電機定子電壓方程為

電機電磁轉矩方程為

由于表貼式PMSM的d-q軸電感相等，所以轉矩方程為

電機的機械運動方程為

式中：ud，uq——d-q的電壓；id，iq——d-q的電流；Ld，Lq——d-q的電感；R——定子電阻；Pn——極對數；φd，φq——d-q的磁鏈；φf——磁鏈；Te——電磁轉矩；TL——電機負載轉矩；J——轉動慣量；we——電角速度；w——機械角速度。

2 滑模變結構控制

2.1 積分型滑模面控制

常用的滑模面函數中包含轉速誤差的微分項，極易產生噪聲以及受外部干擾導致系統抖振[10]。本文設計了積分型滑模面函數，不考慮電機轉速誤差的導數項。積分型滑模面可以使轉矩平滑輸出，有效削弱系統抖振。

滑模控制器為了保證給定轉速wr和實際轉速w的跟蹤誤差最小，定義系統的狀態變量為

式中：e（t）——電機轉速跟蹤誤差；wr——電機給定轉速；w——實際轉速。

選取的積分型滑模面函數為

式中：c——常數，c＞0。

對s求微分，由式（5）—式（8）可得：

2.2 趨近律的設計

采用趨近律的滑模控制算法可以有效削弱系統抖振。對PMSM 而言，常用趨近律有指數趨近律和冪次趨近律等，為提高電機的運行性能，本文結合指數趨近律和冪次趨近律提出的新型趨近律為

式中：ε＞ 0；k＞ 0；0 ＜α＜ 1；=-ks是指數項，其解為s=s（0）e-kt。

可見指數收斂至0，收斂速度取決于k值，指數項-ks能保證當s 較大時，系統狀態能以較大的速度趨近于滑動模態；通過調整α值，可保證當系統狀態遠離滑動模態時，能快速趨近于滑動模態；當系統狀態趨近滑動模態時，保證較小的控制增益，以降低抖振。

2.3 控制量的設計

由式（9）和式（11）可得

整理式（10）—式（12）得滑模控制器的控制量iq的表達式

在滑模變結構控制系統中，符號函數為不連續函數，是造成系統抖振的原因之一。為進一步減弱系統抖振，本文利用飽和函數代替符號函數[12]。飽和函數的表達式為

式中：σ——邊界層。

由式（13）和式（14）整理得控制量為

穩定性驗證：取Lyapunov 函數為V（x）=s2/2，對其求微分得

3 模糊自適應積分滑模控制器（FASMC）

PMSM 調速系統采用傳統趨近律的滑模變結構控制器時，因電機內部參數和外部干擾的變化，很容易影響電機的動態性能，不能保證系統的穩定性，所以采用模糊控制調節新型趨近律的參數，當電機運轉中受到外界干擾和內部參數發生改變時，可以在線自整定新型趨近律中的參數，提高系統的抗干擾能力和穩定性。

FASMC 主要由模糊控制器和積分滑模控制器組成。模糊控制器的輸入為轉速的誤差E和誤差變化率Ec，輸出為滑模控制器中參數的修正值Δk、Δα，實現滑模控制器的實時整定。FASMC算法架構如圖1 所示。

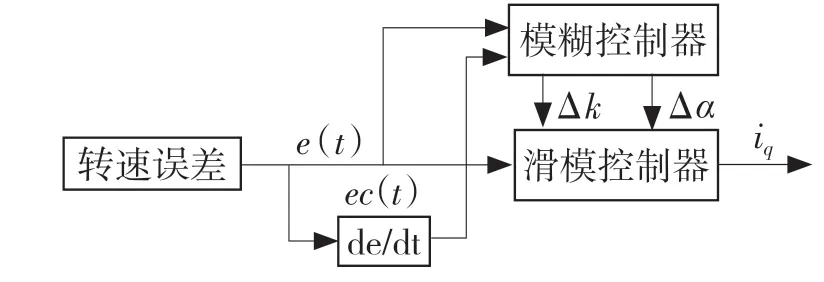
圖1 FASMC 原理框圖Fig.1 Schematic diagram of FASMC

則模糊自適應積分滑模控制器的參數為

式中：k、α——修正后的積分滑模控制器的參數；k1、α1——電機在未啟動前參數的初始值；Δk、Δα——模糊控制根據電機運行時參數實時修正的滑模控制器參數的變化量。

在模糊邏輯控制中最重要的3 個步驟：（1）確定模糊控制器中輸入輸出變量的模糊集合和論域；（2）確定模糊控制器中輸入輸出的隸屬度函數和根據專家經驗得出的模糊控制規則庫；（3）將輸入的清晰量進行模糊化和輸出的模糊量進行逆模糊化。在本文中輸入和輸出變量的模糊集為{負大（NB），負中（NM），負小 (NS)，零（ZE），正小（PS）,正中（PM），正大（PB）}；論域取值為：E∈[-3 3]，Ec∈[-3 3]，k∈[-3 3]，α∈[0 1]，其中模糊化的量化因子的計算和確定參考李曉丹[12]的研究。在模糊控制中2 個模糊集的隸屬度函數曲線交點的值過大會導致控制系統的靈敏度降低，過小則影響控制系統的穩定性，因此該FASMC 選用三角形隸屬度函數，輸入和輸出變量隸屬度函數曲線如圖2 所示。

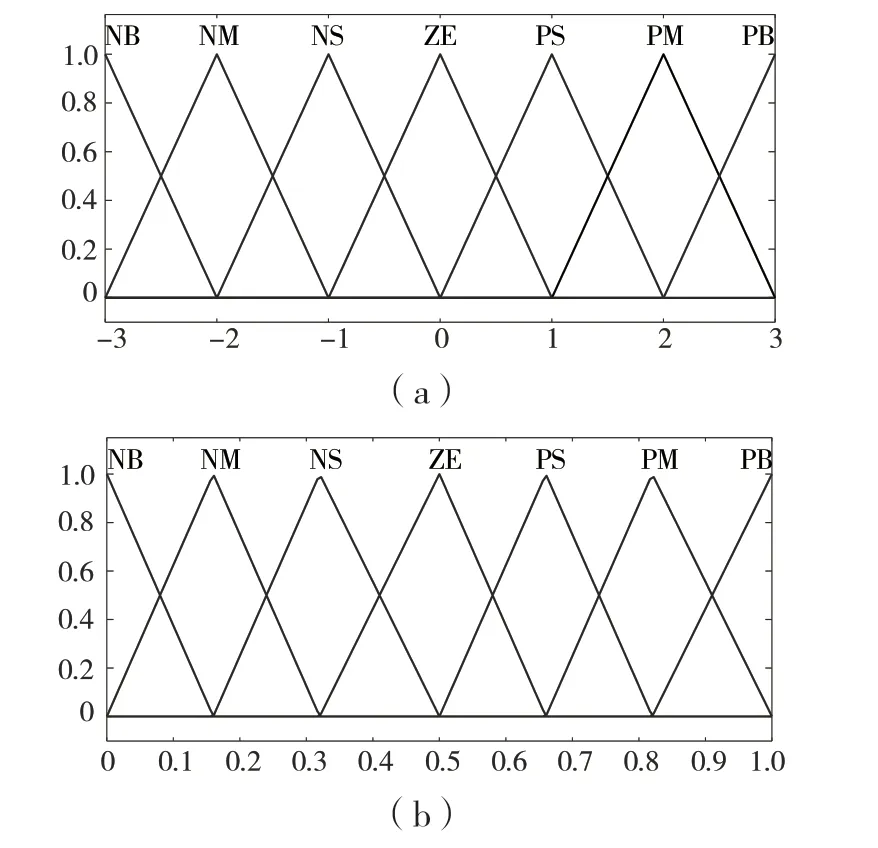
圖2 隸屬度函數Fig.2 Membership function

模糊化的輸入變量經過模糊推理運算得到模糊的輸出變量，對模糊輸出量進行逆模糊化。本文采用重心法進行逆模糊化求解，重心法的表達式為

式中：μ——逆模糊化后的清晰量；μi——各組元素的權重。

根據專家經驗和實驗試湊法確定模糊控制中輸出變量的模糊規則表，如表1 和表2 所示。

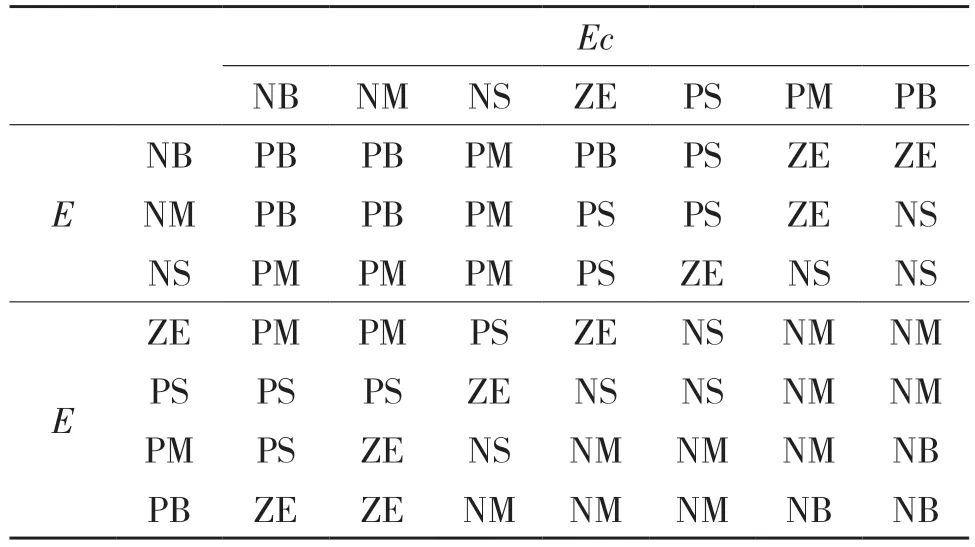
表1 Δα 的模糊控制規則表Tab.1 Fuzzy control rules of Δα

表2 Δk 的模糊控制規則表Tab.2 Fuzzy control rules of Δk

4 MATLAB 仿真與分析

為了驗證FASMC 是否能夠更好地削弱電機空載運行以及電機施加負載時系統的抖振，在MATLAB 中分別對PI、SMC 以及FASMC 進行了仿真對比研究，仿真時電流環調節均采用PI 控制器且參數相同，電機速度環控制采用3 種不同的控制器[13]。仿真系統中對PMSM 的參數設置如表3 所示。

表3 永磁同步電機的參數Tab.3 Parameters of PMSM

仿真條件設置為：直流側電壓Udc=311 V，PWM 開關頻率設置為10 kHz，采樣周期Ts=10 μs，仿真時間為0.4 s。給定轉速為wr=1 000 r/min，初始負載轉矩為0，在0.2 s 時負載轉矩TL=10 N·m。3種控制器參數設置如下：電流環PI 控制器參數，KP=16.4，Ki=5 750；轉速環PI 控制器參數，KP=8，Ki=0.05；指數趨近律的滑模控制器參數，k=300，ε=200；FASMC 的初始參數：A=1 400，B=13 333，k1=0.01，ε=1，α1=0.5，σ=10，c=3 000。

圖3 為電機在PI 控制器、傳統滑模控制器和FASMC 下由啟動到施加負載時的轉速變化曲線。圖4 是在3 種控制器下電機電磁轉矩的變化曲線。圖5 是在3 種控制器下電機變負載時三相電流的響應曲線。由圖3 可以看出，基于FASMC 可以使電機的轉速迅速到達給定值，并在0.02 s 達到穩定，而其他2 種控制器則是在0.07 s 和0.032 s 時系統達到穩定而且有較大的超調量。在0.2 s 時電機增加負載時，PI 控制器和SMC 控制器的電機轉速影響較大，分別在0.22 s 和0.25 s 再次達到穩定，這說明FASMC 控制器有較強的抗干擾能力和魯棒性。

圖3 3 種控制器下變化負載時電機轉速變化曲線Fig.3 Motor speed curve under three controllers with varying load

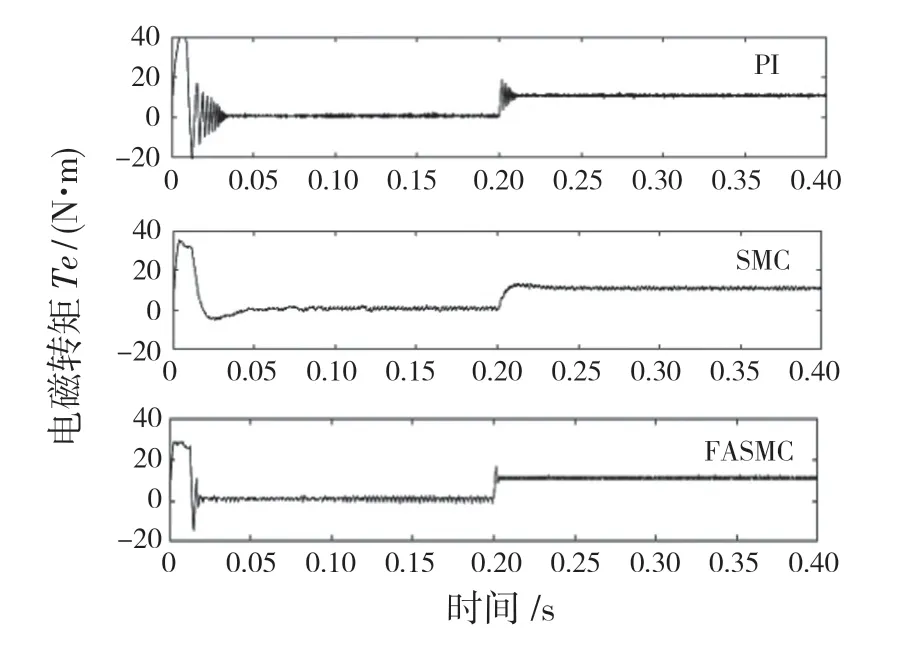
圖4 3 種控制器下電磁轉矩變化曲線Fig.4 Variation curves of electromagnetic torque under three controllers

圖5 3 種控制器下三相電流的響應曲線Fig.5 Response curves of three-phase currents under three controllers

由圖4 可知，PI 控制器在電機啟動時有較大的超調量且在有干擾時電磁轉矩波動較大。雖然SMC 控制器沒有較大的超調量，但是電機達到穩定的時間過長，在電機增加負載時電磁轉矩受影響較大；FASMC 控制器相比其余2 種控制器沒有較大的超調量，且受電機負載干擾的影響較小。

由圖5 電機的三相電流響應波形可知，FASMC 控制器與PI 控制相比沒有較大的超調量，且受電機負載干擾較小，與SMC 控制器相比可以快速地使系統達到穩定。從電機轉速、電磁轉矩和三相電流的變化可以看出，FASMC 可以有效地削弱系統抖振，增強系統的抗負載干擾能力和魯棒性。

5 結論

（1）本文提出一種基于新型趨近律模糊自適應積分滑模控制方法。首先，采用新型趨近律設計系統的滑模控制器；其次，采用飽和函數代替趨近律中的符號函數；最后，采用模糊規則控制對趨近律中的參數進行在線補償。

（2）仿真結果表明，與傳統趨近律的滑模控制和PI 控制策略相比，該控制器不僅能夠有效削弱系統的抖振，而且還可以提高系統的響應速度和增強系統的抗干擾能力，同時也驗證了模糊自適應積分滑模控制策略的正確性和有效性。

本文只考慮了控制方法和參數對永磁同步電機的影響，未考慮外界干擾對電機動態性能的影響。今后將進一步研究外界干擾如何影響電機的動態性能和如何對外界干擾進行補償。