不同格尼襟翼參數對潮流能水輪機翼型水動力學特性影響研究*

劉永輝, 裴 振, 者浩楠, 譚俊哲,3, 袁 鵬,3, 薛 宇

(1.中國海洋大學工程學院,山東 青島 266100;2. 中國海洋大學工程訓練中心,山東 青島 266100; 3. 中國海洋大學 山東省海洋工程重點實驗室,山東 青島 266100)

葉片是潮流能水輪機的主要獲能部件,其性能的優劣直接影響水輪機的發電效率和使用壽命。近年來改善水輪機葉片水動力學性能,提高其發電效率成為潮流能領域的研究熱點之一[1]。設計研發一種高效率的水輪機葉片周期長、造價高,而通過在已有葉片上安裝合適的被動流動裝置,來提高其性能則更為實用。作為一種簡單有效的被動流動控制技術,格尼襟翼(Gurney flap, GF)的結構簡單、增升效果顯著,因而受到了廣泛關注[2]。

格尼襟翼是位于葉片尾緣壓力側,垂直于弦線且高度厚度均較小的一種有效增升裝置[4-7]。格尼襟翼最早應用于賽車后翼板,用來增大賽車的抓地力;后來被成功應用于改善風機葉片的氣動性能[3]。目前格尼襟翼的研究和應用主要集中在風電領域。Chakroun Yosra等[8]研究了格尼襟翼對NACA 4412 翼型性能的影響,結果表明:隨著格尼襟翼高度的不斷增加,翼型的升力系數會逐漸增大,但同時阻力系數也會略有增加。Xi等[9]研究了格尼襟翼對流動分離現象的影響,結果表明:當攻角較小(α≤2°)時,格尼襟翼會抑制翼型表面的流動分離現象;格尼襟翼的存在會增大翼型失速前的升力,并可提高特定攻角下的升阻比。Chen等[10]對有無格尼襟翼的翼型氣動性能進行了分析,結果表明格尼襟翼可以使翼型的最大升力系數提高15.33%,翼型升力的增量同格尼襟翼高度的平方根成正比。

雖然潮流能水輪機同風力機有一定相似之處,但水輪機所處海水的密度大,故不能忽視海水所受重力的影響,且水輪機的工作環境較風力機更為復雜惡劣。目前潮流能水輪機領域主要是通過改變葉片形狀來提高其性能,如袁鵬等[11]基于遺傳算法,利用儒可夫斯基保角變換法對翼型進行參數化建模,從而改善原有翼型的升力系數和升阻比。Shi等[12]結合座頭鯨鰭的前緣結節來改善水輪機葉片的翼型結構,結果表明:前緣結節可使得翼型在失速條件下保持較高的升力系數,并使最大升阻比提高5.8%,但同時還會降低最大升力系數。上述方法雖然可在一定程度上提高葉片性能,但使葉片的設計變得更加復雜。

該文在不改變原始葉片翼型的前提下,于翼型段上安裝格尼襟翼這種附加件,并由此開展格尼襟翼對水輪機葉片水動力學特性的影響規律的研究,以NACA4418翼型為研究對象,研究了不同格尼襟翼參數對水輪機葉片翼型水動力性能的影響規律,通過水槽試驗和數值模擬相結合的方法,驗證了該文研究方法的正確性,所得結論可為格尼襟翼安裝于潮流能水輪機的后續研究提供一定參考。

1 幾何模型

1.1 翼型段

選取NACA4418翼型段為研究對象,該翼型具有較高的升力系數以及較低的阻力系數,因而在潮流能水輪機領域應用比較廣泛[13]。該文采用NACA4418翼型的直翼段,其弦長為300 mm,展向長度為260 mm,基礎翼型段和加裝格尼襟翼后的翼型段分別如圖1(a)、(b)所示。

((a) 基礎翼型段 Basic hydrofoil; (b)帶GF翼型 Hydrofoil with GF.)

1.2 格尼襟翼

格尼襟翼通過增加翼型尾緣的曲率,增大翼型繞流環量,來改善翼型的水動力學性能并提高翼型升力,其具體實現效果同格尼襟翼的幾何參數直接相關[14-19]。格尼襟翼的幾何參數如圖1(b)所示,取襟翼厚度為1 mm,高度、弦向位置(即尾緣長度)以及偏轉角度分別用H、L和Φ表示。

為了驗證格尼襟翼不同幾何參數對翼型水動力學性能的影響,該文共設計了8組模型,分別改變格尼襟翼的高度、弦向位置以及偏轉角度來模擬其性能,8組格尼襟翼模型的數據如表1所示,其中C為葉片翼型弦長。

表1 不同格尼襟翼及其幾何參數

2 數值模擬方法

2.1 數值計算方法

該文采用STAR CCM+商業軟件進行數值模擬計算,該軟件的優點是在網格適應性、計算穩定性和收斂性等方面均具有較好性能[19]。該文將翼型繞流問題看作是不可壓縮流動問題,控制方程選用三維不可壓縮Navier-Stokes方程和三維連續性方程,進行穩態流場計算。湍流模型選擇SSTk-ω湍流模型,該模型具有k-ω模型在近壁區計算和k-ε模型在遠場計算的兩方面優點[22]。

三維連續性方程:

(1)

三維不可壓縮Navier-Stokes方程:

(2)

(3)

(4)

式中:ρ為流體密度(kg/m3);u、v、w分別為x、y、z方向上的速度分量(m/s);t為時間(s);p為壓力(Pa)。

假設葉片翼型的水動力性能參數主要由升力系數Cl、阻力系數Cd以及升阻比Cl/Cd表示,則升力系數Cl的計算公式為:

(5)

阻力系數Cd的計算式為:

(6)

式中:ρ為流體密度(kg/m3);V為來流方向上的速度值(m/s);A為翼型參考面積(m2);Fl為翼型升力(N);Fd為翼型阻力(N);

2.2 計算域和邊界條件

該文采用的計算域如圖2所示,為降低邊界對計算結果的影響,設置計算域入口距離翼型前緣為10倍弦長,計算域出口距離翼型尾緣為20倍弦長,上、下邊界距離翼型均為10倍弦長。計算域左側設置為速度入流邊界,入口速度取1.0 m/s,右側為壓力出口邊界,前、后面為對稱面邊界條件,上、下面和翼型表面為無滑移壁面邊界條件。

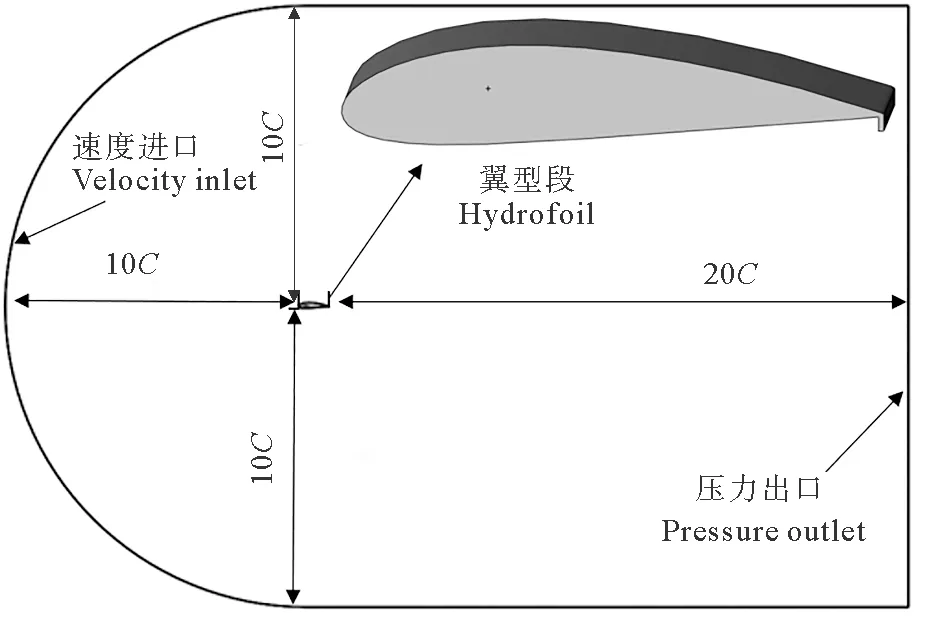
(C:弦長 Chord length.)圖2 整體計算域

2.3 網格劃分

該文采用STAR CCM+軟件特有的多面體網格,其優點是同時具有六面體網格的精確性和四面體網格的易生成性。基礎翼型段和帶格尼襟翼的水輪機葉片翼型段采用相同的網格設置參數,在翼型段表面設置第一層邊界層厚度為0.01 mm,邊界總層數為30,網格增長率取1.3,以保證邊界層y+≤1。為提高仿真結果的準確性,對翼型表面、格尼襟翼及其附近流場的網格進行加密處理(見圖3)。

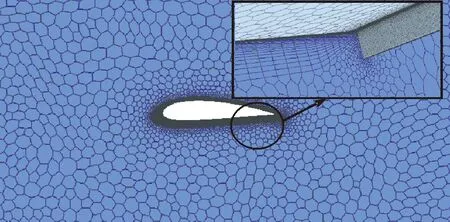
圖3 帶GF翼型段表面附近的多面體網格

2.4 數值模擬及試驗驗證

采用SST k-ω湍流模型,對基礎翼型和加裝不同參數格尼襟翼的翼型進行數值模擬。為驗證數值模擬結果的正確性,本研究通過水槽試驗[20]來加以驗證。試驗在山東省海洋工程重點實驗室進行,實驗水槽長60 m,寬1.2 m,高1 m,最大設計流速可達1.5 m/s,滿足試驗要求。水槽試驗裝置及模型如圖4所示。試驗模型與數值模型一致,均采用弦長300 mm,展長為260 mm的翼型段。當水槽來流速度為1.0 m/s時,對不同攻角下基礎翼型段進行試驗,通過三向力測量儀測量基礎翼型段的升力和阻力。

圖4 實驗場地及翼型段模型

圖5所示為水槽試驗結果與數值模擬結果的水動力學性能對比,可以看出,試驗結果與模擬結果吻合良好。

圖5 翼型段性能試驗數據和數值模擬對比

3 結果與分析

3.1 襟翼高度對翼型性能的影響

對加裝GF1、GF2、GF3的三種翼型段進行水動力學性能分析,其結果如圖6所示。GF1(H=1%C)、GF2(H=3%C)和GF3(H=6%C)是除了高度不同其他參數相同的3個模型,取襟翼厚度為1 mm,尾緣長度L為0%C,偏轉角度Φ為90°。

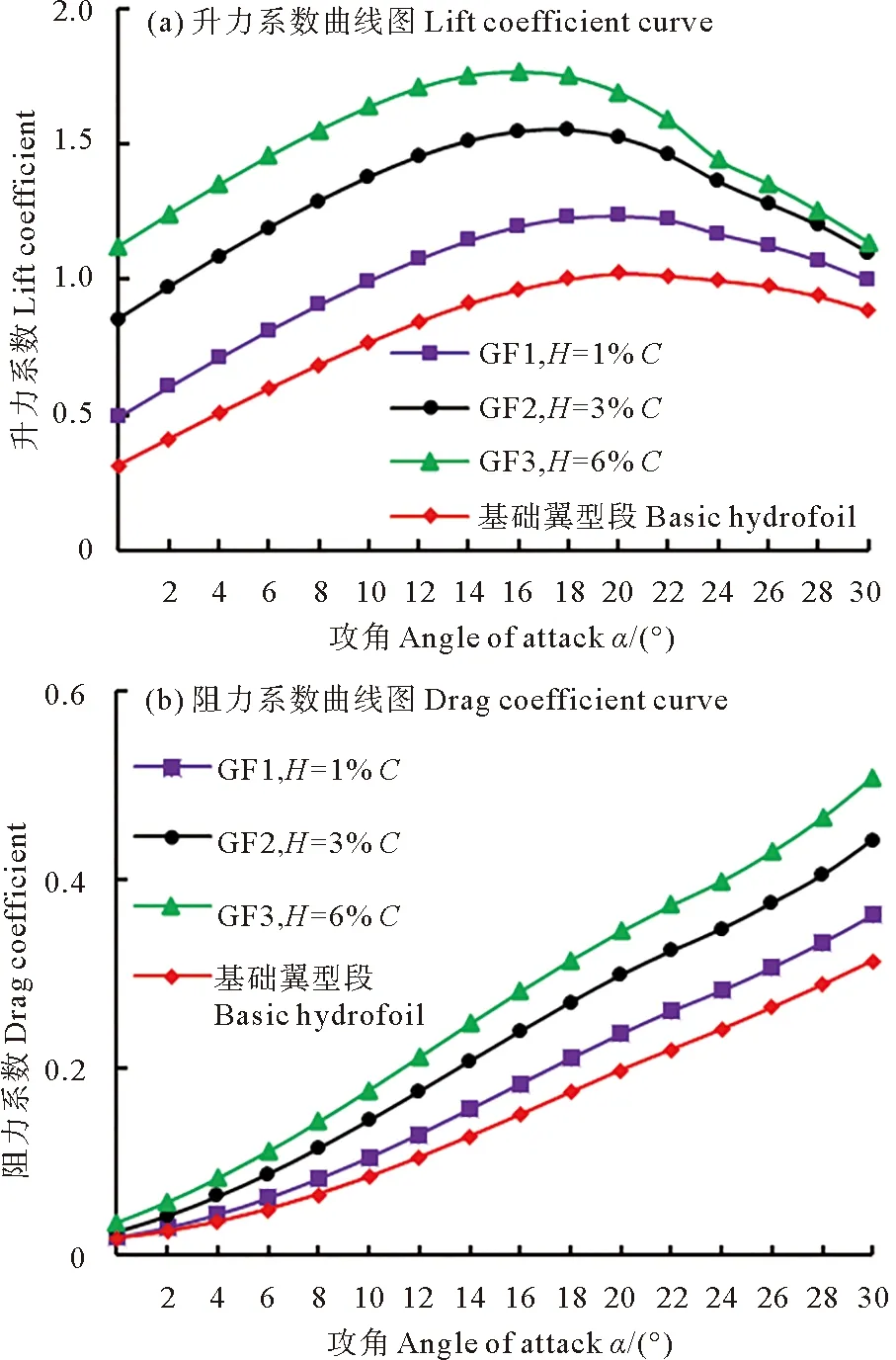
圖6 襟翼高度對翼型水動力學性能的影響

由圖6(a)可以看出,同基礎翼型段相比,加裝格尼襟翼會明顯提高翼型的升力系數,且隨著襟翼高度的增加,翼型升力系數呈非線性增大。對于分別加裝GF1、GF2和GF3的三種翼型段,它們的最大升力系數分別增加了24.08%、60.51%和83.51%;翼型失速后,GF3的升力系數相比于GF2會急劇降低,整體增升效果變差。同時還可以看出,襟翼高度的增加會使翼型失速角降低,而翼型的零升力攻角也有變負的趨勢,這是由于襟翼的存在,增大翼型的有效外傾角和彎度[24]。

由圖6(b)可以看出,襟翼的存在還會增大翼型段的阻力系數,且襟翼高度越高,阻力系數越大。對于分別加裝GF1、GF2和GF3的三種翼型段,它們的最大阻力系數分別增加了15.53%、41.03%和72.08%,且阻力增加的幅度會隨著高度的增加而增大。綜合分析可知,存在一個最佳襟翼高度可使得翼型段獲得最佳的水動力學性能,針對此模型,GF2對翼型段的性能提升最明顯。

為進一步揭示格尼襟翼對水輪機葉片翼型水動力學性能的作用機理,圖7給出了最大升力系數(α=16°)下,不帶襟翼和帶不同高度格尼襟翼模型的流線圖。由圖7可看出,加裝襟翼使得翼型上表面流線更貼合吸力面。一方面,這是由于在襟翼后方生出一對反向渦,其內上方順時針轉動的渦,會誘導翼型段上表面流體在尾緣處向下偏轉,從而增大上表面的繞流環量和邊界層抵抗逆壓梯度的能力;另一方面,襟翼下方逆時針轉動的渦則會抵消壓力面繞流的部分能量,從而降低流速。通過伯努利定理中流速和壓強的關系可知,襟翼高度的增加會增大翼型上下表面的壓差和升力,但是當格尼襟翼高度增大到一定程度即GF3(H=6%C)時,其高度已遠大于此翼型的邊界層厚度,此時尾流區內反向渦的尺寸和尾流區面積都急劇增加(見圖7c),導致翼型的阻力隨之增大[5],襟翼的增升效果變差。

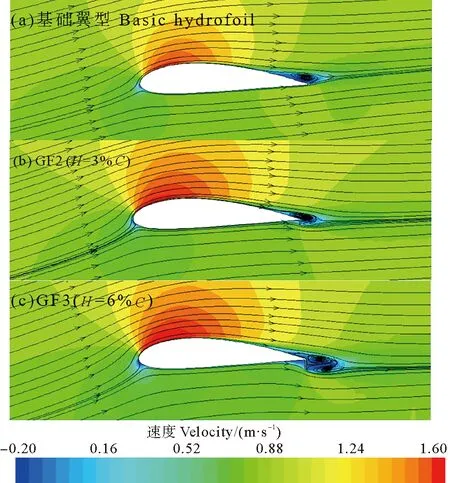
圖7 α=16°時,不同襟翼高度對翼型流場的影響

如圖8所示,分別為基礎翼型段和加裝高度分別為3%C和6%C襟翼的翼型段壓力云圖。可以看出,在加裝GF后,壓力面的尾緣襟翼前方會出現高壓區域,并顯著增大下表面的壓力,而襟翼后方則出現低壓區域;吸力面的前緣附近產生更小的負壓區,且上表面的整體壓力變小。這是由于襟翼高度的增加相當于尾緣的延伸,從而提高翼型的有效彎度,導致翼型吸力面的壓力增大和壓力面壓力減小,即翼型的升力隨襟翼高度的增加而增大。

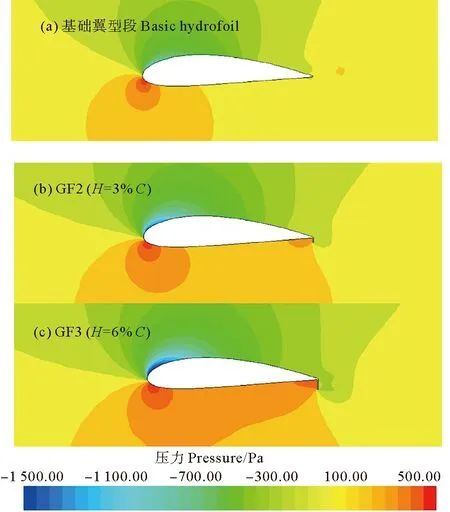
圖8 α=16°時,襟翼高度對翼型表面靜壓力的影響

圖9為16°攻角時不同高度下,沿弦長方向翼型表面的壓力散點圖。可以看出,隨著襟翼高度的增加,翼型上表面負壓明顯降低,上表面前緣的吸力增大;下表面的壓力逐漸增大,而在翼型表面壓力分布圖中,曲線所圍面積可表示翼型的升力大小[25],即翼型段的升力逐漸增大。但當高度超過一定值(H=3%C)時,曲線所圍面積的增加幅度會變小,此時再增加高度會降低襟翼的增升效果。

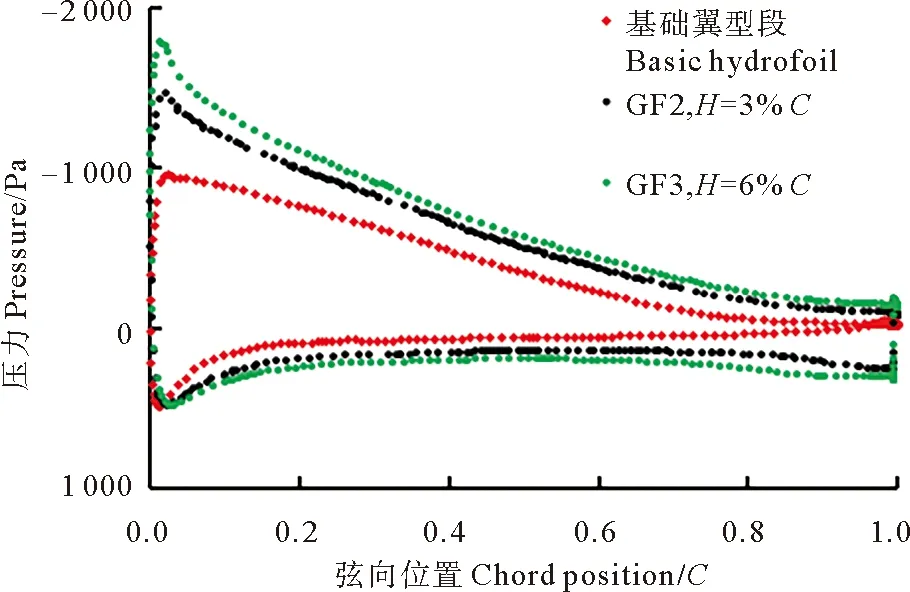
圖9 α=16°時,襟翼高度對翼型表面壓力影響

3.2 襟翼弦向位置對翼型性能的影響

對加裝GF2、GF4、GF5、GF6的四種翼型段進行水動力學性能對比分析,其中GF2 (L=0%C)、GF4 (L=15%C)、GF5(L=10%C)、GF6 (L=15%C)是除弦向位置不同其余參數相同的4個模型,取厚度為1 mm,高度H為3%C,偏轉角度Φ為90°,所得升阻力系數變化如圖10所示。

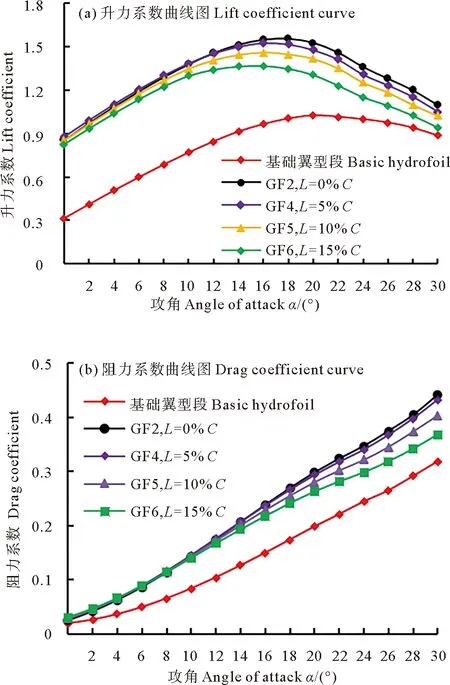
圖10 襟翼弦向位置對翼型水動力學性能的影響

由圖10(a)可知,隨著襟翼遠離尾緣位置,翼型的失速角略有降低,而在翼型失速前,襟翼位置對升力系數的影響較小;失速后,隨著襟翼遠離尾緣位置,其升力系數會顯著降低。同時,對于分別加裝GF2、GF4、GF5和GF6的4種翼型段,它們的最大升力系數分別增加了60.51%、58.27%、51.34%和41.73%。由圖10(b)可以看出:在翼型失速(α=16°)前,阻力系數幾乎不發生變化;在翼型失速后,隨著襟翼遠離尾緣,阻力略有減小。此時加裝GF2、GF4、GF5和GF6的翼型段的最大阻力系數分別增加了41.01%、38.03%、28.84%和17.46%。但是考慮到隨著襟翼遠離尾緣位置,升力系數會顯著降低,且尾緣位置處的失速角降低的最少,故尾緣位置處的格尼襟翼最能改善翼型的水動力性能。

圖11為α=16°時,不同襟翼弦向位置下的翼型速度流場圖。可以看出,隨著襟翼遠離尾緣位置(0～15%C),尾流區內上方的渦受襟翼的影響降低,上表面的流速略有下降,襟翼對上表面流體的引導作用減弱,繞流環量減小。而尾流區內下方的渦明顯成型,湍流強度增大,下表面流速有所增加。據伯努利定理中速度和壓力的關系可知,翼型上下表面的壓差減小了,即襟翼的增升效果變差。

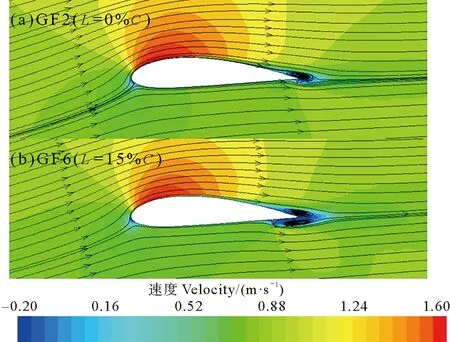
圖11 α=16°時,GF弦向位置對翼型流場的影響

圖12為α=16°時,不同襟翼弦向位置處的翼型壓力云圖對比。可以看出,隨著襟翼遠離尾緣位置,翼型尾緣附近的高壓區面積減小,壓力降低,甚至在襟翼后方出現負壓區域,導致翼型上下表面壓差變小。同時襟翼的前移相當于降低翼型的有效彎度,使得襟翼的增升效果降低。

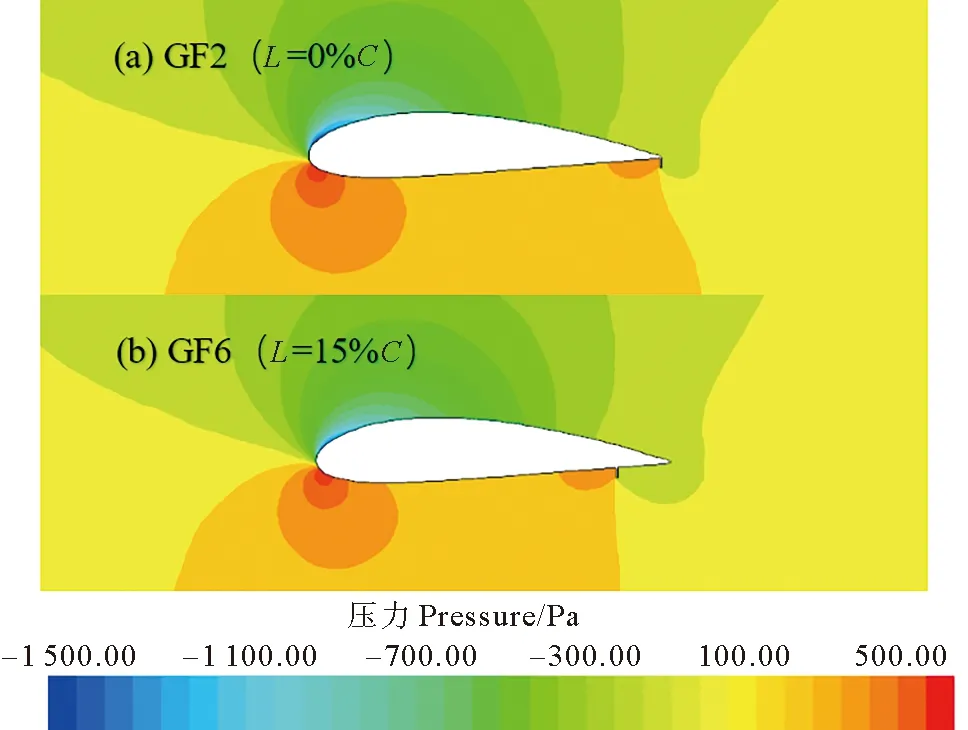
圖12 α=16°時,GF弦向位置對翼型表面壓力影響 Fig.12 Effect of GF chord position on static pressure distribution of hydrofoil at α=16°

圖13為α=16°時,不同弦向位置下,沿弦長方向翼型表面的壓力散點圖。由圖13可知,隨襟翼遠離尾緣位置,上表面的壓力略有降低,下表面前部分壓力幾乎不變,但在弦向0.6C～0.85C的范圍內壓力有所增加,同時襟翼后方的正壓值則會急劇降低,直至為負。從整體上看,弦向位置的變化會使曲線所圍面積減小,降低翼型的升力系數和增升效果。

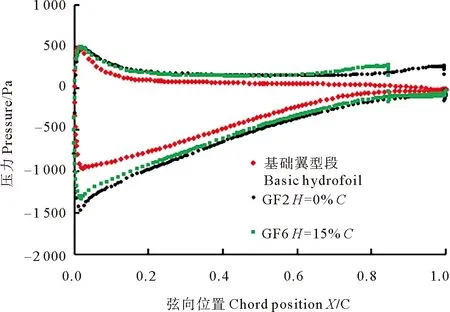
圖13 α=16°時,弦向位置對翼型表面壓力影響

3.3 襟翼偏轉角度對翼型性能的影響

對分別加裝GF2、GF7和GF8的3種翼型段進行水動力學性能分析,其中GF2(Φ=90°)、GF7(Φ=45°)和GF8(Φ=120°)是除偏轉角度不同其余參數相同的3個模型,高度H為3%C,弦向位置L為0%C,其結果如圖14所示。由圖14(a)可以看出,隨著偏轉角度的贈加,升力系數先增大后減小,加裝GF2的翼型段所獲升力系數最大,且分別加裝GF7、GF2和GF8的三種翼型段的最大升力系數分別增加了55.60%、60.51%和49.85%,其中加裝GF2的翼型段所獲升力系數最大。由圖14(b)和(c)可以看出,隨著偏轉角度的增加,阻力系數和升阻比變化不明顯。

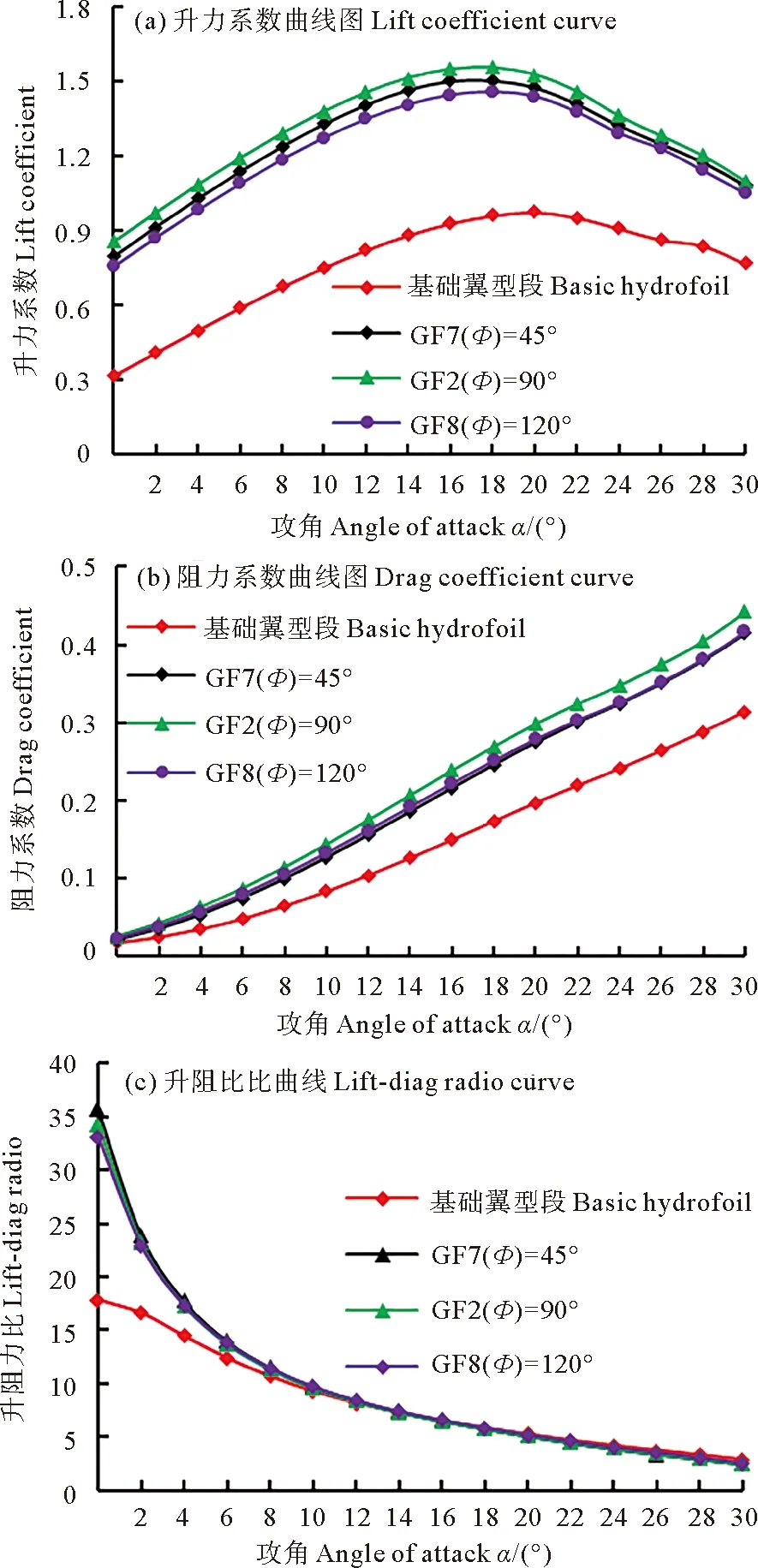
圖14 襟翼偏轉角度對翼型水動力學性能的影響

圖15為α=16°時不同偏轉角度下,翼型的速度流線圖。由圖可知,隨著偏轉角度的增加,上表面的深色區域面積先增大后減小,即在GF2(Φ=90°)時上表面流速最大,而下表面的流速幾乎不發生變化。綜上所述,當襟翼偏轉90°(即GF2)時翼型可獲得最大的升力,即增升效果最佳。

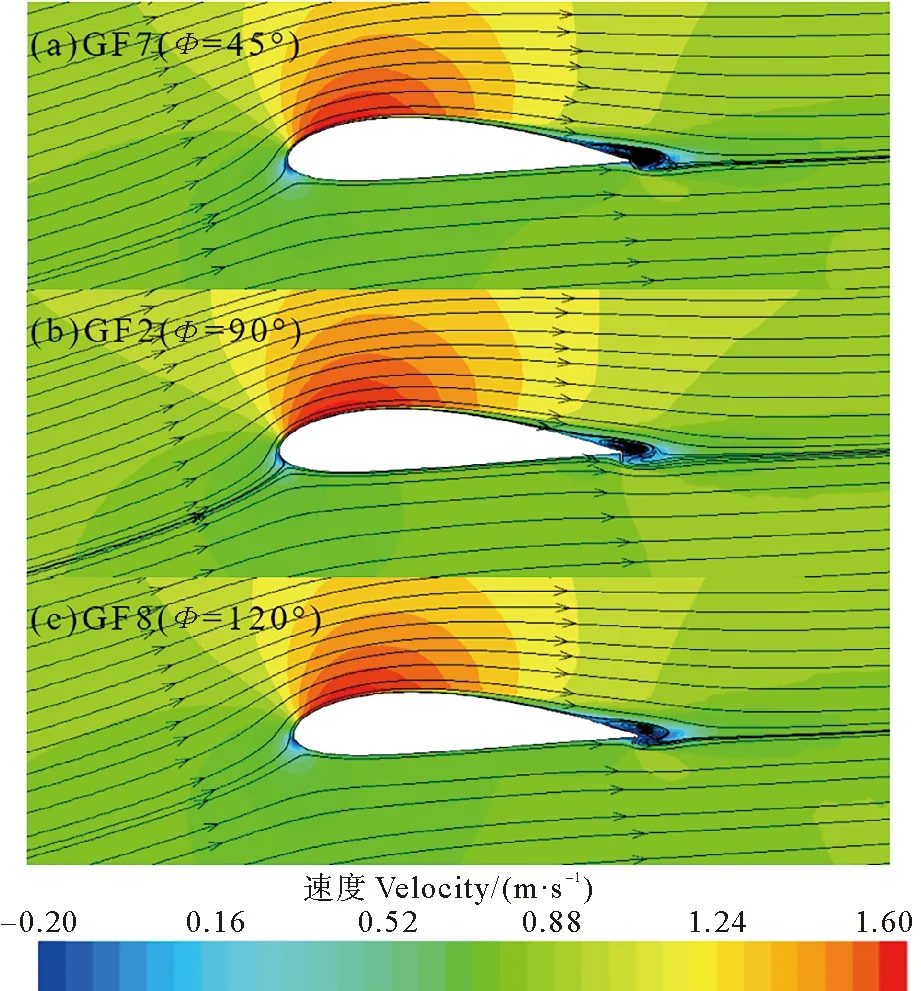
圖15 α=16°時,偏轉角度對翼型流場的影響

4 結論

(1) 格尼襟翼可以有效地改善翼型段的水動力性能,提高翼型的最大升力系數,但翼型段的失速角會有所降低,同時阻力系數也略有增大。

(2) 在本次研究中,研究了不同格尼襟翼高度、弦向位置以及偏轉角度對葉片翼型水動力學性能的影響,其中GF2(H=3%C,L=0%C,Φ=90°)的改善效果最佳,其最大升力系數增加了60.51%,這說明合理的格尼襟翼參數設置可有效地提高翼型的水動力學性能。

(3) 該文的研究結果能夠為格尼襟翼應用于改善水輪機葉片翼型的水動力學性能提供理論指導,在上述基礎上還需對加裝格尼襟翼后翼型的失速角降低現象進行優化,并開展格尼襟翼對水輪機三維扭曲葉片水動力學特性的影響研究,這將是本研究團隊下一步研究工作的重要內容。