基于K近鄰算法的鋼筋混凝土柱地震破壞模式判別方法
楊程, 顏海泉, 董正方*
(1.河南大學土木建筑學院, 開封 475004; 2.上海市政工程設(shè)計研究總院(集團)有限公司, 上海 230031)
鋼筋混凝土(reinforced concrete,RC)柱作為工程中常見的承重結(jié)構(gòu)[1],在建筑結(jié)構(gòu)工程中發(fā)揮著重要的作用,受到地震作用會呈現(xiàn)三種不同的破壞模式(彎曲破壞、彎剪破壞、剪切破壞),對工程結(jié)構(gòu)造成重大影響[2]。不同的破壞模式會導(dǎo)致RC柱地震損傷特征具有差異性[3]。所以,通過尋找參數(shù)與破壞模式之間的規(guī)律,并建立一種合適的地震破壞模式判別方法,更有利于鋼筋混凝土結(jié)構(gòu)抗震性能評價和加固的開展。
目前,RC柱的地震破壞模式判別方法大致可以分為傳統(tǒng)經(jīng)驗法和機器學習法二大類。傳統(tǒng)經(jīng)驗法主要對實驗數(shù)據(jù)歸納與分析,將某一個參數(shù)或者多個參數(shù)與地震破壞模式聯(lián)系起來。例如,文獻[4-5]分別基于單一的抗剪需求與抗剪承載力之比或者剪跨比給出了RC柱不同地震破壞模式的判別區(qū)間;文獻[6]則以軸壓比、剪跨比、箍筋參數(shù)、縱筋參數(shù)4個參數(shù)以概率方法提出一種綜合判斷指標判別法,并給出了判別表達式。經(jīng)驗法的特點是使用方便,但判斷結(jié)果可靠性較低[7]。
近幾年機器學習在土木工程方向發(fā)展較為迅速[8],與傳統(tǒng)經(jīng)驗法方法相比,其優(yōu)點是可以通過探索參數(shù)與3種地震破壞模式之間存在的某種內(nèi)在聯(lián)系。例如,文獻[9]對比了6種不同機器學習算法對地震破壞模式判別精度;文獻[10]基于樸素貝葉斯分類算法建立了RC柱地震破壞模式的判別方法;文獻[11]建立了隨機森林算法與RC柱地震破壞模式之間的關(guān)系。上述機器學習方法在一定程度上比傳統(tǒng)經(jīng)驗法準確率要高,但是仍存在以下不足:一是數(shù)據(jù)集樣本不均衡時,導(dǎo)致機器學習算法對少數(shù)類破壞模式判別精度較低[12];二是沒有篩選出最佳參數(shù),所建立的模型常常將所有的參數(shù)作為模型輸入指標,會導(dǎo)致使用判別模型時較復(fù)雜。例如,文獻[9]在使用K-近鄰(K-nearest neighbor,KNN)方法建立模型時沒有進行參數(shù)的篩選,導(dǎo)致計算模型復(fù)雜,判別準確率較低。因此,需要均衡少數(shù)類樣本數(shù)據(jù)集,篩選出使RC柱地震破壞模式判別模型準確率達到最佳的參數(shù),并建立相應(yīng)的地震破壞模式判別模型。
現(xiàn)首先基于合成少數(shù)過采樣技術(shù)(synthetic minority over-sampling technique,SMOTE)算法生成初始均衡數(shù)據(jù),接著依據(jù)編輯近鄰(edited nearest neighbours,ENN)算法分別篩選出判別彎曲破壞和非彎曲破壞、彎剪破壞和剪切破壞的最佳參數(shù);通過TomekLinks算法合理剔除噪音樣本,然后根據(jù)篩選的最佳參數(shù)并結(jié)合KNN算法[13],建立兩階段KNN模型,達到準確判別RC柱破壞模式的目的。通過與傳統(tǒng)KNN模型以及3種傳統(tǒng)經(jīng)驗法做對比,驗證模型所提模型的優(yōu)異性。
1 處理不平均衡數(shù)據(jù)的算法
SMOTE算法主要是利用將少數(shù)類樣本通過人工合成新的樣本來對其進行擴充,從而使整個樣本達到均衡。RC柱破壞模式不平衡數(shù)據(jù)問題可以描述為
Tm+n={Am,Bn}
(1)
Am={Ai|i=1,2,…,m}
(2)
Bn={Bi|i=1,2,…,n}
(3)
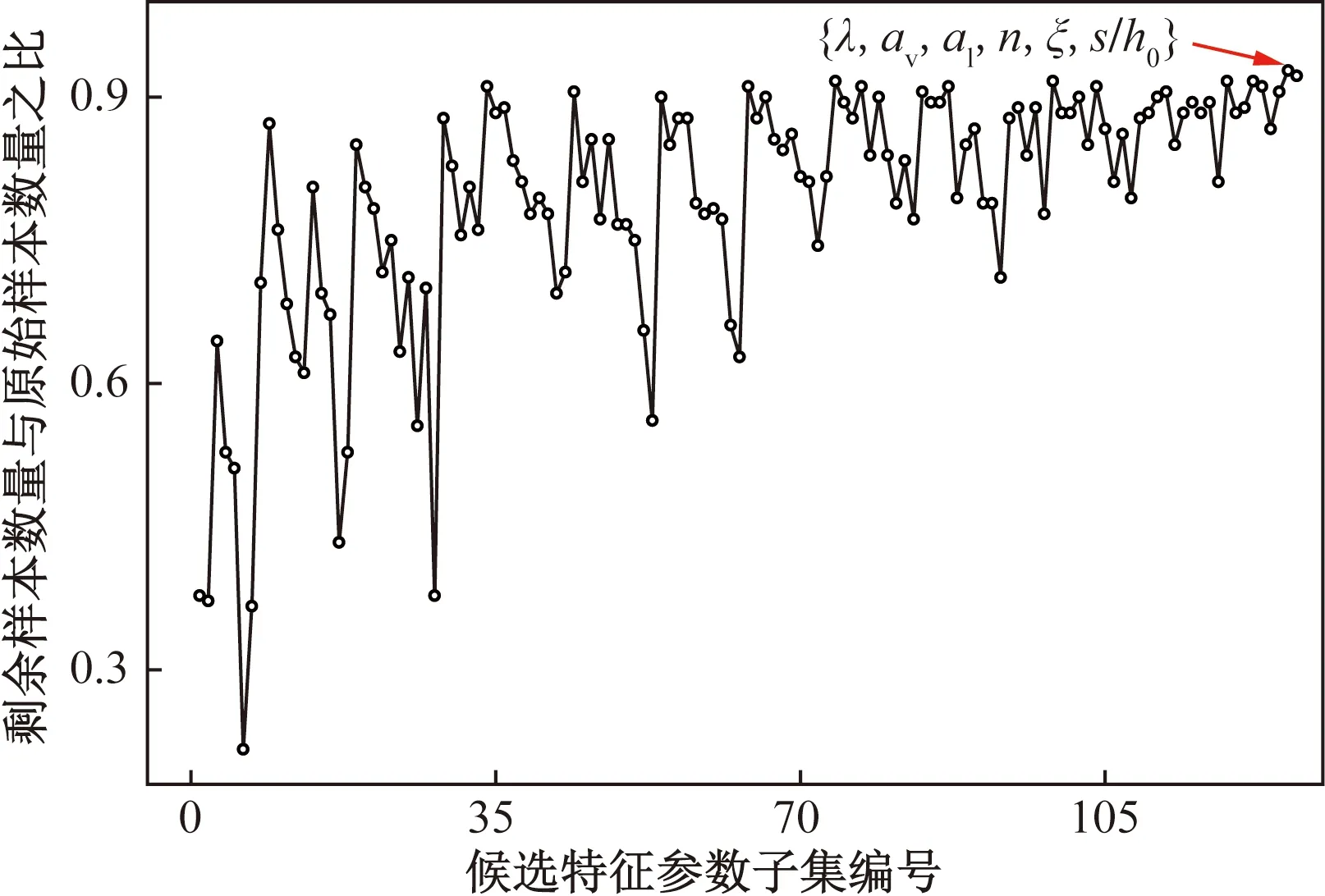
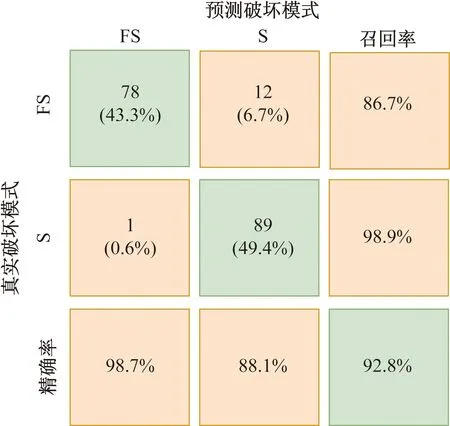
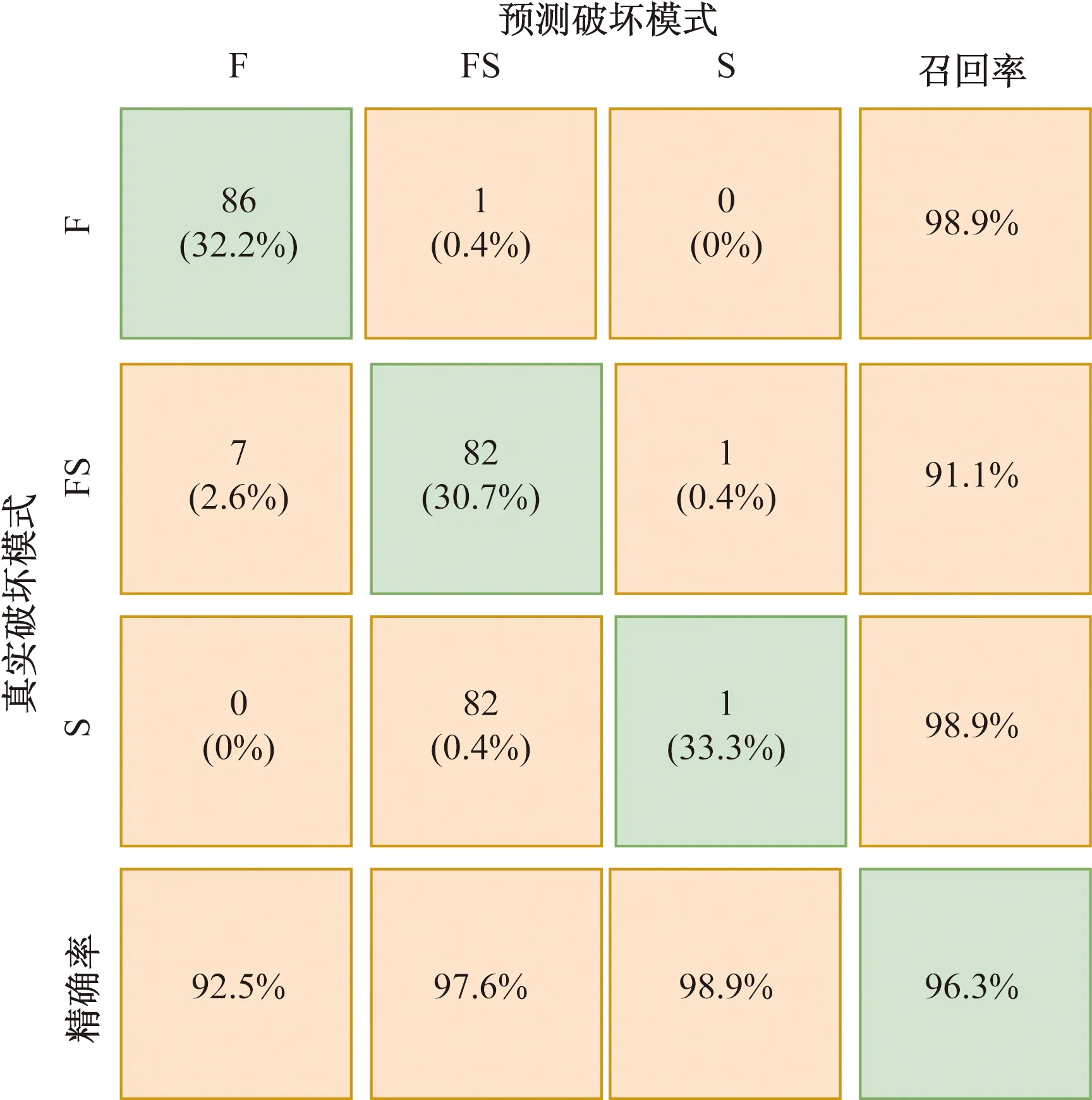
式中:Tm+n為不平衡數(shù)據(jù)集;Am為少數(shù)類破壞模式的數(shù)據(jù)集(如剪切破壞或彎剪破壞);Bn為多數(shù)類破壞模式數(shù)據(jù)集(如彎曲破壞);Ai和Bi分別為少數(shù)類樣本和多數(shù)類樣本的第i個樣本點;m和n分別為少數(shù)類和多數(shù)類破壞模式數(shù)據(jù)集的樣本個數(shù),且m 如圖1所示,根據(jù)SMOTE算法[14]選定與Ai距離最近的ki個同類樣本點Aik(k=1,2,…,ki),在樣本點Ai與Aik之間可以合成新樣本點A′ik,表達式為 圖1 基于SMOTE算法的過采樣過程Fig.1 Oversampling process based on SMOTE A′ik=Ai+η(Aik-Ai) (4) 式(4)中:η為(0,1)的隨機數(shù)。對于少數(shù)類樣本數(shù)據(jù)集Am中的每個樣本Ai(i=1,2,…,m),可以根據(jù)式(4)隨機合成ki個新樣本點。所以使用SMOTE算法進行采樣,可以將少數(shù)類樣本個數(shù)由m個調(diào)整到n個,進而達到初始平衡數(shù)據(jù)。 不同參數(shù)對RC柱的地震破壞模式影響程度不盡相同,目前較為常用的有抗剪需求與抗剪承載力之比(Vp/Vn)[4]、剪跨比(a/h0)[5]、縱箍筋相對量(ξ=∑Aslfy/∑Asvfyv)[15]、縱筋參數(shù)(αl=ρlfy/f′c)、箍筋參數(shù)(αv=ρvfyv/ft)、軸壓比(n)[6]、箍筋間距與截面有效高度比(s/h0)[16]等。其中a為剪跨,h0為截面有效高度,∑Asl為柱子截面的單側(cè)受拉縱筋的面積,∑Asv為柱高范圍內(nèi)所有箍筋的截面面積之和,fyv為箍筋的屈服強度,fy為縱筋的屈服強度,ρl為配筋率,f′c為混凝土抗壓強度,ρv為配箍率,ft為混凝土抗拉強度,s為箍筋間距。為了探究上述7個參數(shù)與RC柱地震破壞模式之間的關(guān)系,從PEER數(shù)據(jù)庫[17]中收集了148組(彎曲破壞90組、彎剪破壞33組和剪切破壞25組)圓形截面RC柱的破壞試驗數(shù)據(jù)。 為了驗證SMOTE算法生成數(shù)據(jù)集的合理性,得到不同地震破壞模式下各參數(shù)的小提琴圖如圖2所示。其中。分析圖2可知,SMOTE算法生成數(shù)據(jù)不會改變原始數(shù)據(jù)集數(shù)據(jù)分布特點,說明SMOTE算法生成數(shù)據(jù)具有一定合理性;另外從圖2中可以看出,參數(shù)Vp/Vn、s/h0、ξ和αl越大,或者αv和a/h0越小,RC柱的越容易發(fā)生剪切破壞;反之RC柱越容易發(fā)生彎曲破壞;參數(shù)n對3種破壞模式并沒有特別大的影響。 F為彎曲破壞RC柱,FS為彎剪破壞RC柱,S為剪切破壞RC柱;小提琴外部形狀為核密度估計圖;每個小提琴圖中的虛線從下到上分別為該樣本中所有數(shù)值由小到大排列后第25%、50%、75%的數(shù)字圖2 各參數(shù)在不同地震破壞模式下的小提琴圖Fig.2 Violin diagram of characteristic parameters for different earthquake failure modes 為了進一步分析參數(shù)對RC柱地震破壞模式的影響,得到各參數(shù)不同破壞模式之間數(shù)據(jù)均值的增長率或減少率(以剪跨比為例,彎曲破壞均值為4.56、彎剪破壞均值 2.01、剪切破壞均值為1.33,則彎曲破壞到彎剪破壞的減少率為56%、彎剪破壞到剪切破壞的減少率為34%)如表1所示。 表1 各參數(shù)不同破壞模式之間增長率或減少率Table 1 Change rate of different failure modes of different parameters 由表1可知,通過觀察各種參數(shù)的之間的變化率,可以看出不同特征之間變化率差異比較明顯,所以需要考慮不同參數(shù)對地震破壞模式的影響;通過觀察同一參數(shù)不同破壞模式之間變化率,可以看出變化率也比較大,所以有必要將破壞模式進行分開研究,分別研究不同破壞模式之間參數(shù)對其影響。 綜合以上分析研究,首先分別篩選出第一階段和第二階段RC柱地震破壞模式的最佳參數(shù),根據(jù)最佳參數(shù)分別建立不同階段的判別模型,具體判別流程如下:第一階段判別RC柱是發(fā)生彎曲破壞還是非彎曲破壞,根據(jù)第一階段的結(jié)果判斷是否進行第二階段,第二階段需要針對非彎曲破壞進一步判斷,判別RC柱是發(fā)生彎剪破壞還是剪切破壞。 ENN[18]算法是對數(shù)據(jù)集每一個樣本采用KNN模型檢測,若檢測結(jié)果與實際類別標簽相悖,則認為該樣本為噪聲樣本,并剔除相應(yīng)樣本。最終是基于KNN算法做判別模型,針對上述7個參數(shù)總計127(即27-1)參數(shù)組合情況,對于每一種組合情況采用ENN進行去噪,通過剩余樣本數(shù)量與原始樣本數(shù)量的比值大小來確定最佳組合,考慮到ENN算法去噪原理是基于KNN算法,剩余樣本數(shù)量與原始樣本數(shù)量比值越大就說明該組合選取越合理,這樣使KNN算法做判別模型的效果達到最好。上述7個參數(shù)都是無量綱的,因此可以排除量綱對本文模型的影響。但是通過上述小提琴圖可以看出不同的參數(shù)的取值范圍有著較大差異,這樣會導(dǎo)致取值范圍較大的參數(shù)會比取值范圍較小的參數(shù)在模型訓練中提供更多的信息,導(dǎo)致對判別的結(jié)果有影響。因此,為了消除此影響,對每個參數(shù)的取值范圍做了規(guī)定,即 (5) 式(5)中:A為原始參數(shù);Amin為原始參數(shù)中的最小值;Amax為原始參數(shù)中最大值;A′為處理后的數(shù)據(jù)。 為篩選第一階段模型(用來判別彎曲破壞和非彎曲破壞)的最佳參數(shù),根據(jù)前述7個參數(shù)組成的原始參數(shù)集{Vp/Vn,s/h0,a/h0,αl,ξ,n,αv}生成127(27-1)個參數(shù)候選子集;根據(jù)180組試驗數(shù)據(jù)(彎曲破壞和非彎曲破壞都為90組),通過ENN算法,得到結(jié)果如圖3所示。當候選參數(shù)子集編號k為41時(此時參數(shù)子集為{Vp/Vn,αv,n}),剩余樣本數(shù)量與初始樣本數(shù)據(jù)比值達到最高;隨著k不斷增大,比值并不會有較大的變化,甚至還會有降低的趨勢;所以第一階段kNN模型最佳參數(shù)子集為{Vp/Vn,αv,n}。 圖3 第一階段最佳參數(shù)的篩選Fig.3 The selection of optimal characteristic parameters in the first stage 同理,為了篩選出第二階段模型(用來判別彎剪破壞和剪切破壞)的最佳參數(shù),采用由前述7個參數(shù)組成的原始參數(shù)集{Vp/Vn,s/h0,a/h0,αl,ξ,n,αv}生成的127個參數(shù)候選子集;基于180組試驗數(shù)據(jù)(彎剪破壞和剪切破壞都為90組),通過ENN算法,其結(jié)果如圖4所示。隨著k的增加,剩余樣本數(shù)量與初始樣本數(shù)量的比值整體呈增大趨勢,當候選參數(shù)子集編號k為126時(此時參數(shù)子集為{λ,αl,αv,n,ξ,s/h0}),剩余樣本數(shù)量與初始樣本數(shù)據(jù)比值達到最高。所以,第二階段KNN模型最佳參數(shù)子集為{λ,αl,αv,n,ξ,s/h0}。 圖4 第二階段最佳參數(shù)篩選Fig.4 Optimal feature parameter selection in the second stage 綜上所述,對于彎曲破壞和非彎曲破壞,可以通過{Vp/Vn,αv,n}3個參數(shù)來建立判別模型,對于彎剪破壞和剪切破壞可以通過{λ,αl,αv,n,ξ,s/h0} 6個參數(shù)來建立判別模型。通過上述參數(shù)篩選,對于彎曲破壞與非彎曲破壞(彎剪破壞與剪切破壞)從原始的7個參數(shù)簡化到3個參數(shù),對于彎剪破壞與剪切破壞從原始7個參數(shù)簡化到6個參數(shù),一定程度上簡化了判別模型。 基于SMOTE算法進行過采樣合成少數(shù)類樣本數(shù)據(jù)集的過程中會有隨機性,會產(chǎn)生噪聲數(shù)據(jù)樣本點,干擾分類器的分類性能,導(dǎo)致判別精度下降。TomekLinks[19]算法是一種欠采樣算法;TomekLinks算法會剔除每對 TomekLink(如果A和B分別來自兩個不同類別的樣本且A和B互為最近,A和B就為一對TomekLink)中的多數(shù)類樣本,假如兩個樣本個數(shù)一樣多,則會剔除這一對。 當建立第一階段模型(判別彎曲破壞和非彎曲破壞) 時,對174組(經(jīng)過TomekLinks算法剔除噪聲樣本后,其中彎曲破壞和非彎曲破壞都為87組)RC柱地震破壞模式樣本數(shù)據(jù)基于KNN算法進行分類,通過10折交叉驗證得到判別RC柱地震破壞模式的第一階段KNN模型的混淆矩陣如圖5所示。 F為彎曲破壞RC柱,FS為彎剪破壞RC柱,S為剪切破壞RC柱;精確率表示預(yù)測樣本中真實樣本所占的比例,召回率表示真實樣本被預(yù)測正確比例;混淆矩陣對角線上的綠色格上數(shù)值代表正確判別個數(shù),帶括號的百分數(shù)為正確樣本個數(shù)占總樣本的百分比,不帶括號的百分數(shù)為樣本的總體判別準確率;橙色格上的數(shù)值代表錯誤判別的個數(shù),帶括號的百分數(shù)為錯誤樣本個數(shù)占總樣本的百分比,不帶括號的百分數(shù)分別代表各自破壞模式的精確率和召回率圖5 第一階段KNN模型Fig.5 The first stage KNN method 對于第一階段KNN模型,彎曲破壞樣本有2個樣本被誤判為非彎曲破壞,非彎曲破壞樣本有9個樣本被誤判為彎曲破壞,模型整體準確率為93.7%。由此可見,第一階段KNN模型的判別準確率相對較高。 當建立第二模型(判別彎剪破壞和剪切破壞)時,對180組(經(jīng)過TomekLinks算法剔除噪聲樣本后,其中彎剪破壞和剪切破壞都為90組)RC柱地震破壞模式樣本數(shù)據(jù)基于KNN算法進行分類,通過10折交叉驗證得到最終結(jié)果。其結(jié)果如圖6所示。圖6中,對于第二階段KNN模型,彎剪破壞樣本有12個樣本被誤判為剪切破壞,剪切破壞樣本有1個樣本被誤判為彎剪破壞,模型整體準確率為92.8%。由此可見,第二階段KNN模型的判別準確率相對較高。 圖6 第二階段KNN模型Fig.6 The second stage KNN method 為了驗證本模型的最終準確率,將實驗的267組數(shù)據(jù)(彎曲破壞87組,彎剪破壞90組,剪切破壞90組)用上述兩階段模型進行判別,得到判別結(jié)果的混淆矩陣如圖7所示。 圖7 兩階段KNN模型最終結(jié)果Fig.7 Final result of two-stage KNN model 由圖7可知,兩階段KNN模型對3種破壞模式(彎曲破壞、彎剪破壞、剪切破壞)召回率和精確率都較高,分別為98.9%、91.1%、98.9%和92.5%、97.6%、98.9%,整體準確率是96.3%,由此說明本文模型的誤判率較低,對于3種破壞模式判錯率都低于10%。 本文模型可以通過輸入鋼筋混凝土柱設(shè)計參數(shù)進行判斷,第一階段需要通過輸入{Vp/Vn,αv,n} 3個參數(shù)來進行判別,判別RC柱的破壞模式是否是彎曲破壞,假如是彎曲破壞則不需要進行第二階段判別,假如不是彎曲破壞則需要進行第二階段判別,第二階段通過輸入{λ,αl,αv,n,ξ,s/h0} 6個參數(shù)來判別RC柱發(fā)生彎剪破壞還是剪切破壞。 為了驗證兩階段KNN模型準確率的優(yōu)異性,將該方法與傳統(tǒng)KNN模型、3種傳統(tǒng)經(jīng)驗法[4-6](表2)判別性能進行對比分析。用148組RC柱破壞模式實驗樣本(F:90組、FS:33組、S:25組)去驗證傳統(tǒng)KNN模型以及3種傳統(tǒng)經(jīng)驗法(分別記為模型1、模型2、模型3)的準確率,得到的判別結(jié)果如圖8所示。 表2 傳統(tǒng)經(jīng)驗法RC柱破壞模式判別方法Table 2 Traditional empirical method to distinguish failure mode of RC column 由圖8(a)可知,傳統(tǒng)KNN模型對彎曲破壞、彎剪破壞、剪切破壞判別錯誤個數(shù)分別為5、12、4,召回率分別為94.4%、63.6%、84.0%,精確率分別為92.4%、70.0%、80.7%,模型整體的準確率為85.5%,可見傳統(tǒng)KNN模型對于彎曲破壞和剪切破壞判別準確率較高,對于彎剪破壞判別準確率較低;由圖8(b)可知,模型1對彎曲破壞、彎剪破壞、剪切破壞判別錯誤個數(shù)分別為12、20、4,召回率分別為86.7%、39.3%、84.0%,精確率分別為92.9%、46.4%、58.3%,模型1整體的準確率為75.7%,可見模型1對于彎曲破壞和剪切破壞判別準確率較高,對于彎剪破壞判別準確率較低;由圖8(c)可知,模型2型對彎曲破壞、彎剪破壞、剪切破壞判別錯誤個數(shù)分別為27、18、5,召回率分別為70.0%、45.5%、80.0%,精確率分別為100%、41.7%、40.8%,模型2整體的準確率為62.2%,可見模型2模型對于彎曲破壞和剪切破壞判別準確率較高,對于彎剪破壞判別準確率較低;由圖8(d)可以看出,模型3對彎曲破壞、彎剪破壞、剪切破壞判別錯誤個數(shù)分別為0、30、10,召回率分別為100%、9.1%、60%,精確率分別為81.8%、37.5%、50%,模型3整體的準確率為73.0%,可見模型3對于彎曲破壞和剪切破壞判別準確率較高,對于彎剪破壞判別準確率較低。說明傳統(tǒng)KNN模型、模型1、模型2、模型3這4種方法對于彎曲破壞樣本和剪切破壞樣本一定程度上能夠準確判別,但是彎剪破壞樣本被誤判較多。所以上述4種模型雖然一定程度上能夠?qū)澢茐臉颖竞图羟衅茐臉颖具M行正確判斷,但是對于彎剪破壞樣本判別準確率較低,不能夠兼容整體上的準確率。 綜合以上分析,傳統(tǒng)的KNN模型、基于抗剪需求與抗剪承載力之比判別模型、基于剪跨比判別模型、多參數(shù)判別模型不能夠同時保證3種破壞模式有著較高的準確率,有較多彎剪破壞樣本被誤判,從而使彎剪破壞精確率和召回率較低,而本文模型不僅能夠很大程度上提升彎剪破壞模式準確率,對于彎曲破壞模式和剪切破壞模式也有一定程度的提升,而且3種破壞模式的精確率和高召回率都可達90%以上。 通過處理不平衡數(shù)據(jù)、篩選最佳參數(shù)、剔除噪聲樣本等手段對KNN模型改進,并進行了方法之間的對比,得到下列結(jié)論。 (1)通過SMOTE算法生成的平衡數(shù)據(jù),并根據(jù)ENN算法,篩選出了第一階段和第二階段KNN模型的最佳參數(shù),分別為{Vp/Vn,αv,n}、{Vp/Vn,s/h0,a/h0,αl,ξ,n,αv}。 (2)通過引入TomekLinks算法,來尋找樣本中的TomekLink對,可以有效剔除在初始平衡數(shù)據(jù)集生成階段產(chǎn)生的噪聲數(shù)據(jù),從而獲得高質(zhì)量的平衡數(shù)據(jù)。 (3)兩階段KNN模型對于RC柱的3種破壞模式召回率和精確率以及整體準確率均可達到90%以上,比傳統(tǒng)KNN模型整體判別準確率大約高10%,比基于抗剪需求與抗剪承載力之比判別模型整體準確率和多參數(shù)判別模型整體準確率高20%左右,比基于剪跨比判別模型整體準確率高34%。 本文方法不僅適用于RC柱的破壞模式判別,也可以用于其他鋼筋混凝土構(gòu)件破壞模式的判別以及其他同類型的問題;另外隨著樣本數(shù)量增加,本文模型精度會進一步提高。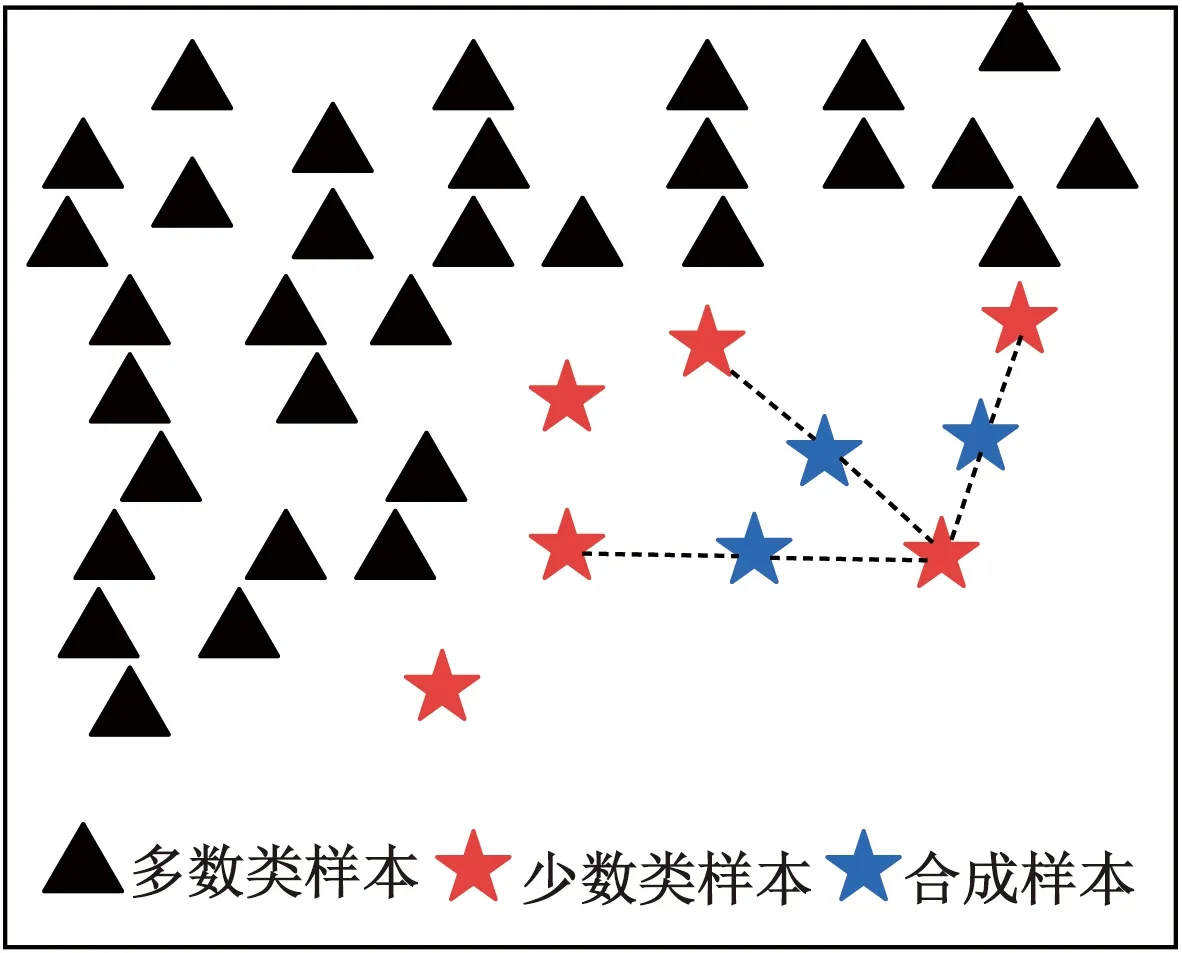
2 地震破壞模式參數(shù)分析
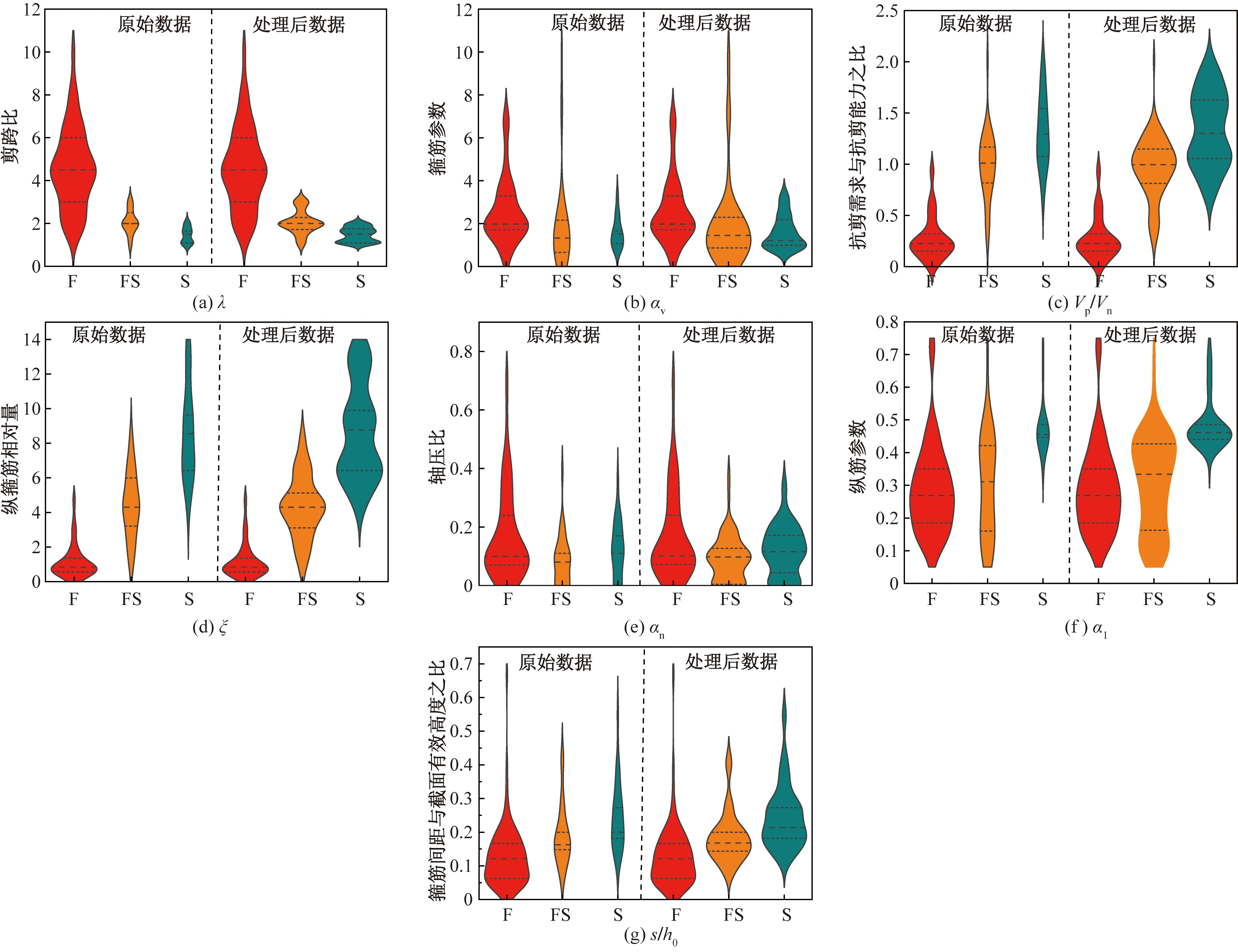
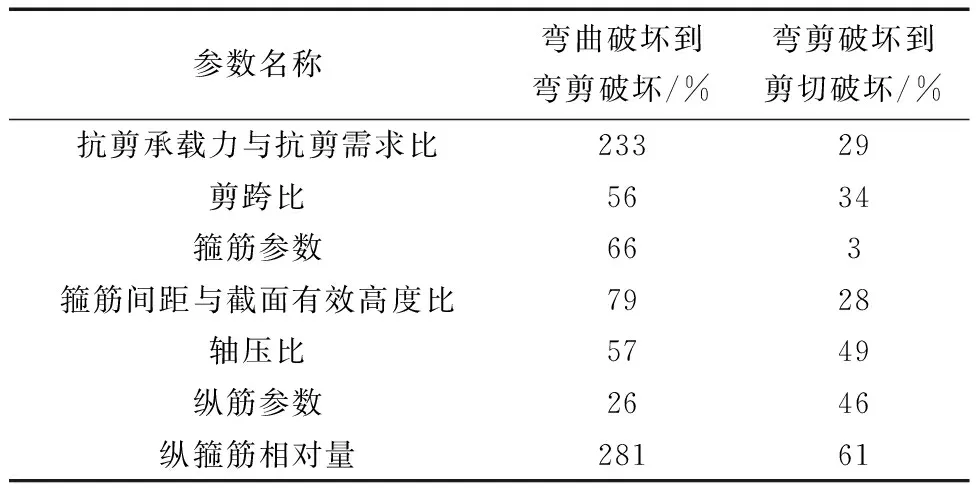
3 最佳參數(shù)篩選
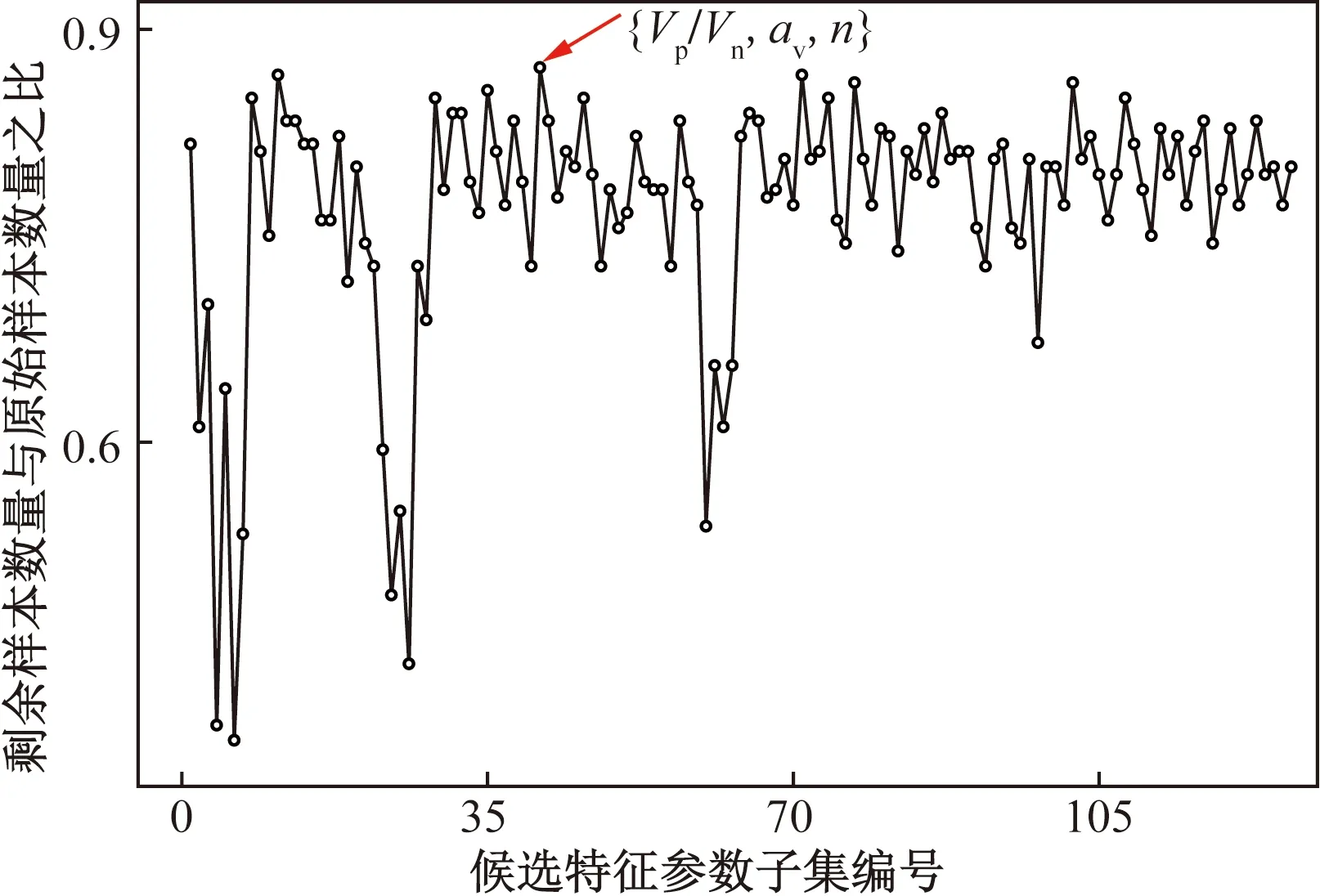
4 地震破壞模式判別的兩階段模型

5 對比驗證分析

6 結(jié)論

