基于事件相機的連續光流估計

付婧祎 余 磊 楊 文 盧 昕

光流(Optical flow,OF)估計一直是圖像處理與計算機視覺領域中一個核心的研究課題.近年來,隨著計算機軟硬件水平的提高,各類光流估計算法層出不窮,光流技術在跟蹤[1-2]、運動分割[3-4]、導航[5-6]和圖像配準[7-8]等應用領域凸顯出了越來越重要的作用.特別是在高速運動場景中,由于空間物體運動位置的快速變化,對運動數據的獲取和光流的計算提出了更高要求,連續且高精度的光流估計算法[9]更是被國內外學者廣泛研究,其獲得的光流估計結果也能為后續各類視覺任務打下良好基礎.

然而,由于相機自身較低的時間分辨率,傳統光學相機在高速運動場景下,難以連續捕捉到物體在成像平面中位置的快速變化,導致輸出圖像幀存在運動模糊,因此低幀率的數據使得基于傳統相機的光流估計算法無法有效地進行連續的光流估計.如圖1(a)所示,向右做高速運動的棋盤格由傳統光學相機成像,由于傳統相機曝光時間較長,棋盤格在亮度圖像幀中出現了運動模糊.通過傳統Horn-Schunck 算法[10]獲得的光流結果如圖1(b)所示,隨著棋盤格運動速度加快,受到亮度圖像運動模糊的影響,傳統算法所估計的光流精度逐漸降低,甚至輸出與實際運動反向的光流結果.

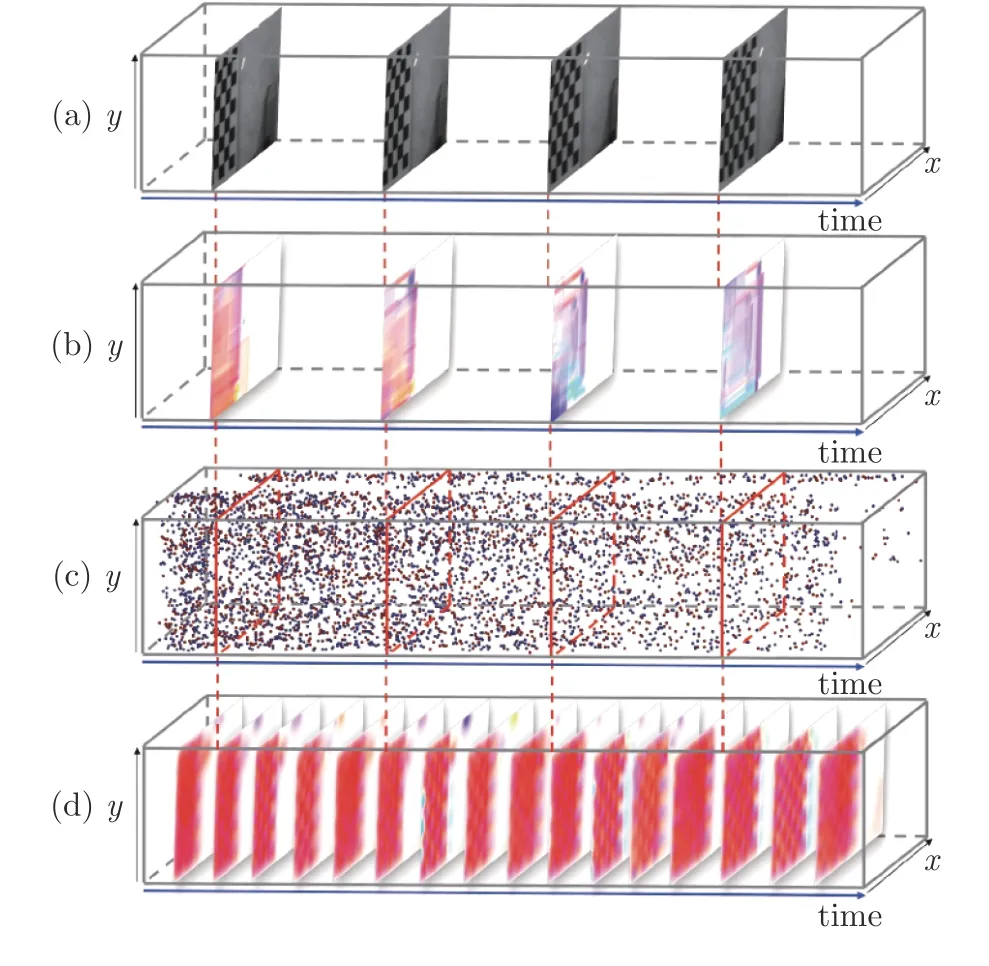
圖1 基于傳統相機和基于事件相機的光流估計效果對比((a)傳統相機輸出圖像幀序列;(b)傳統Horn-Schunck算法的光流估計結果;(c)事件相機輸出事件流;(d)本文EDI-CLG 算法光流估計結果)Fig.1 Comparison of traditional camera and event camera based optical flow ((a)The samples of images acquired by traditional camera;(b)The results using Horn-Schunck algorithm;(c)The event data generated by event camera;(d)The results using the proposed EDI-CLG algorithm)

近年來,針對基于傳統光學相機的光流估計算法易受運動模糊影響的問題,基于事件相機[11-12]的光流估計算法受到了廣泛關注.事件相機是一種新型的仿生傳感器,不同于傳統相機通過固定時間間隔采樣獲取圖像幀,該相機具有獨立的像素,這些像素只在場景的亮度變化超過一定閾值時異步地進行成像.此外,事件相機具有高時間分辨率的特性,受運動模糊問題影響較少[13],因此能夠對空間物體的運動進行連續捕捉,獲取瞬時的運動數據有利于進行連續的光流估計.圖1(c)展示了棋盤格高速運動生成的事件點,紅色表示亮度增強,藍色表示亮度減弱.可以看出,事件相機捕捉到的運動信息在時間上具有連續性,基于此估計出的如圖1(d)所示的光流結果,不僅在時間上具有連續性特征,而且更加精確.

目前,基于事件相機的光流估計算法主要分為單純基于事件流算法和聯合事件流與亮度圖像算法兩種.由于事件流數據不能如圖像幀一樣完整地反映場景的紋理信息,因此單純基于事件流的光流估計算法[14-16]僅能反映事件點觸發位置的光流信息,無法得到完整的場景運動信息.此外,由于事件數據存在大量噪聲[17],也降低了光流估計的準確性.動態和主動像素視覺傳感器(Dynamic and activepixel vision sensor,DAVIS)相機由Berner 等[18]開發.該傳感器結合了動態視覺傳感器(Dynamic vision sensor,DVS)[19-20]和傳統的主動像素傳感器(Active pixel sensor,APS),不僅輸出異步事件流,還可以輸出固定幀率的亮度圖像.基于此,Almatrafi 等[21]提出了聯合DVS 和APS 數據的光流估計方法,提高了事件相機光流估計的準確性和魯棒性.然而,由于APS傳感器輸出的亮度圖像依然不可避免地受到運動模糊影響且該算法由于依賴亮度圖像獲取空間梯度,只能估計出建幀時刻的非連續光流,因此并不能保證高速運動場景下光流的精度和連續性.

針對上述問題,本文基于亮度恒定假設和事件產生模型利用事件相機輸出事件流的低延時性質,融合存在運動模糊的亮度圖像幀,提出基于事件相機的連續光流估計算法.通過研究模糊圖像幀與曝光時間內生成事件點之間的關系,可以重建出連續的清晰亮度圖像,從而使算法受運動模糊的影響較少.最后在計算光流時,添加平滑約束獲得更具魯棒性的稠密光流,最終實現高速運動場景下受運動模糊影響較小的連續光流估計.

本文的主要貢獻如下:

1)針對基于傳統光學相機的光流估計算法易受運動模糊影響問題,本文通過研究模糊圖像幀與曝光時間內生成事件點之間的關系,理論上推導了聯合事件和圖像的連續光流模型,建立了任意時刻光流、圖像和事件之間的關系.

2)基于聯合事件和圖像的連續光流模型,提出HS (Horn-Schunck)和結合局部與全局(Combining local and global,CLG)平滑約束的光流估計方法,提升了重建光流的精度和平滑性.

3)通過實驗表明,本文方法不僅能夠較大提升基于事件相機光流估計的精度,同時還能解決目標高速運動條件下如何進行連續且穩定的光流估計問題.因此,對于高速運動的極端場景,本文方法具有一定優勢.

1 相關算法概述

1.1 基于傳統相機的光流估計

在基于傳統相機的光流估計方法中,光流可以通過連續圖像幀間的相關性以及圖像上特定像素在空間和時間上的變化得到.一般地,坐標 (x,y)上的像素在t時刻的亮度值可以表示為I(x,y,t),為簡便起見,有時將I的坐標變量默認省略.在環境不變時,用同一相機拍攝的圖像序列之間有很強關聯性,因此可以引入光流的“亮度恒定”假設[10,22]即隨著時間的變化,在圖像平面移動的像素點亮度值不變.對于t時刻在坐標 (x,y)上的像素點,經過?t時間,移動到 (x+?x,y+?y),則:

基于這一假設,將式(1)按一階泰勒展開后,再忽略高階項,可以得到光流約束方程:

但僅有光流約束方程不足以估計出二維運動場.因此,Horn 等[10]通過正則化方式提高全局空間的一致性,提出速度平滑假設,將問題轉化為可求解的凸函數,也就是HS 光流法.Lucas 等[22]提出基于光流場局部空間一致性的Lucas-Kanade 光流,提高算法的準確性和魯棒性.隨后,Black 等[23]提出分段平滑的假設來改進全局平滑,黃波等[24]通過引入二維標號場改進了HS 光流.Fortun 等[25]則通過最小化光流的大小來引入額外的約束,進一步提升了算法的精度.

然而,由于傳統相機的時間分辨率較低,在某些高速運動的極端場景下,容易出現運動模糊,導致光流估計算法的性能急劇下降.因此基于傳統相機的光流估計算法無法有效地保證高速運動場景下光流估計的準確性和穩定性.針對運動模糊問題,現有方法大多數基于線性運動的假設,在此基礎上,通過求解模糊問題得到相應的光流估計[26-27].但是,由于場景運動較為復雜,無法滿足線性運動假設,從而影響光流估計的精度[28].

1.2 事件相機成像原理

事件相機是受生物視覺系統啟發的一類新型視覺傳感器,與傳統相機存在一定區別.傳統相機基于幀進行成像,輸出同步圖像幀,像素點代表場景的絕對亮度;事件相機基于像素點獨立成像,輸出包含大量事件點的異步事件流,事件流表示場景在對數域的亮度變化.事件點數據包含了亮度變化事件的像素坐標、觸發時間和極性三類信息.在像素平面上,若像素u=(x,y)T在t時刻上的對數光強值與上一時刻的對數光強值之差超過一定的閾值C,則激發事件e:=〈u,t,p〉:

式中,V:=lgI表示圖像對數域的亮度值;閾值C >0;?t是距離該像素上一次激發事件經過的時間;p∈{1,-1} 表示事件的極性,p為正表示光強增強,為負表示光強減弱.

與逐幀成像的傳統相機相比,逐像素點獨立成像的事件相機延時極低,能夠及時響應像素的亮度變化并輸出事件流,從而記錄任意時刻的亮度變化情況.事件相機的低延時性質,使其特別適用于高速和高動態范圍場景的視覺任務,例如自動駕駛[29]、高速同時定位與地圖構建[30]、光流估計等.

1.3 基于事件相機的光流估計

針對基于事件相機的光流估計問題,目前常見方法是將恢復圖像像素強度作為預處理步驟,以適應傳統算法.如Benosman 等[14]利用短時間內事件的逐像素直方圖來代替像素值,Bodo 等[31]使用中心差分來改善空間梯度的質量,Tobias 等[32]則利用空間梯度和時間梯度之間的耦合來提高魯棒性.但由于從事件到強度轉換過程中信息的丟失,這些算法與基于幀的光流估計算法相比,精度較差.

另一種常見方法是利用事件相機的特性來估計光流.Gallego 等[15]通過圖像對比度最大化,以產生運動補償的圖像來同時估計光流和深度.Lagorce等[16]開發算法來擬合時空流形以估計平滑的邊緣運動.Liu 等[33]提出一種基于事件的塊匹配算法來估計光流的方向,并在文獻[34]中融合了速度的計算.Barranco 等[35]提出一種基于相位的方法來計算高頻紋理區域的光流,并嘗試重建強度信號,以避免紋理邊緣處可能存在的問題.Bardow 等[36]通過建立窗口,將亮度恒定和平滑先驗組合為代價函數,并通過變分法進行優化,實現光流和亮度的估計.這些算法在一定程度上提高了光流估計的精度,但由于事件流數據不能如圖像幀一樣完整地反映場景的紋理信息,因此基于事件相機的光流估計算法僅能反映事件點觸發位置的光流信息,無法得到完整的場景運動信息.

近年來,聯合事件生成模型和“亮度恒定”假設進行光流估計的方法[37]得到了廣泛關注.其中,部分方法基于事件的二重積分(Event-based dou-ble integral,EDI)模型[38],如Pan 等[39]利用該模型提出了聯合光流估計和亮度圖像去模糊算法,實驗結果表明,利用EDI 模型可以降低運動模糊的影響,有利于提升光流估計的精度.因此,本文算法同樣基于EDI 模型,并通過結合事件流和亮度圖像各自的優勢,提出基于事件相機的連續光流估計算法,以解決現有的傳統光流估計算法易受運動模糊的影響,以及單純基于事件流的光流估計算法空間信息不足的問題.

2 基于事件相機的連續光流估計

本節研究基于事件相機的連續光流估計方法,結構安排如下: 第2.1 節簡要介紹EDI 模型,第2.2 節推導聯合EDI 模型和“亮度恒定”假設的連續稀疏光流估計方法,第2.3 節分別添加兩種平滑約束,最終求得對噪聲具有魯棒性的連續稠密光流場.

2.1 EDI 模型

EDI 模型[38]利用事件點的高時間分辨率優勢,可以重建出受運動模糊影響較少的連續清晰亮度圖像.相機APS 模塊具有曝光時間,因此其輸出的亮度圖像在相機或場景內運動目標做高速運動的情況下,會產生運動模糊.假定第i幀亮度圖像為Y[i]∈RM×N,曝光時間為T,曝光起始時刻用ti表示,則圖像生成模型可以表示為:

式中,I(t)表示在t∈R時刻的瞬時清晰亮度圖像,這個生成模型可以解釋為由于亮度圖像I(t)在T時間內的快速變化,導致輸出圖像Y[i] 模糊.為了更直觀地表示事件,用連續時間信號來定義離散事件序列,對于像素平面上的每一個像素 (x,y),定義exy(t)為連續時間t的函數:

式中,δ(·)表示狄拉克函數,te表示事件被激發的時刻.定義I(f)是f時刻的瞬時清晰亮度圖像,結合式(4)和式(6),可得:

將式(7)代入亮度圖像生成模型式(5),可以得到曝光時間內的模糊圖像與事件點,以及時刻f的瞬時清晰亮度圖像之間的關系:

然后,可以定義:

最終,可將式(8)寫為:

式中,Ei(f)表示第i幀亮度圖像曝光時間內生成事件點的二重積分,I(f)表示任意時刻f的瞬時清晰亮度圖像,兩者均在時間上具有連續性特征.式(10)將模糊圖像、瞬時清晰亮度圖像和事件點之間建立了聯系.而模糊圖像和事件點是已知的,就可以通過式(10)計算出任意時刻的瞬時清晰亮度圖像.

2.2 基于EDI 模型的連續光流估計

EDI 模型僅僅考慮了模糊圖像的去模糊問題,本節進一步結合光流約束方程研究基于EDI 模型的連續光流估計問題.

若將EDI 模型重建出的瞬時清晰亮度圖像看作式(3)中的亮度圖像I,即:

則亮度圖像I對時間f求導得:

可以結合式(3)和式(10),推導出聯合事件流和亮度圖像的連續光流估計方法:

則式(12)可更新為:

最終,將式(14)代入式(13),求得基于連續清晰亮度圖像重建的光流計算公式:

上式給出了任意時刻f的連續光流v(f)與模糊圖像Y[i] 和事件流數據Ei(f)之間的關系.第2.3節中,將利用這個關系并結合平滑約束,進一步得到優化的光流估計.

2.3 平滑約束的連續光流估計

2.3.1 HS 平滑約束的連續光流估計

HS 光流法是一種基于全局的方法[40],它除了需要滿足Lucas-Kanade 光流法的亮度恒定、時間連續和運動位移小的假設外,還需要滿足圖像光流場全局平滑的假設.使用I簡化表示I(f),令光流矢量v=(v1,v2),定義一個能量函數:

式中,Ix、Iy和If分別表示圖像I在x、y方向上的導數和對時間的導數,?表示求梯度,該能量函數的 (Ixv1+Iyv2+If)2是灰度變化因子,α(|?v1|2+|?v2|2)是平滑因子,α為正則化參數,調節光流場的平滑程度,理想的光流場應該使得灰度變化因子和平滑因子之和最小,即亮度恒定且運動平滑.為了便于推導,令:

將L對v1和v2分別進行求導,得:

式中,? 是拉普拉斯算子操作,可表示為:

本文用以下公式代替:

式中,(x,y)為m(x,y)的拉普拉斯估計值:

進行拉普拉斯操作替換后,將式(19)更新為:

使用Gauss-Seidel 迭代方法[40],利用估計的空間梯度、時間導數和上一次迭代的速度估計結果來計算一組新的速度估計值,得到迭代式:

本文實驗中選取λθ=1×10-6.具體算法見算法1.其中,時間間隔 ?f將每一幀亮度圖像的曝光時間T進行T/?f等分,決定了T時間內的連續光流估計次數.

2.3.2 CLG 平滑約束的連續光流估計

通常情況下,基于局部的光流估計方法對噪聲更具魯棒性,而基于全局的光流估計方法則產生更加精確的稠密光流場.CLG 光流法[41]結合了局部方法和全局方法各自的優勢,產生對噪聲具有魯棒性的稠密光流場,其最小化能量函數可以表示為:

式(26)中各個參數的定義如下:

式中,Kρ是高斯核,ρ表示高斯核的鄰域窗口大小,“?”表示卷積操作,參數α調節平滑程度.使用類似第2.3.1 節中HS 平滑約束迭代公式的推導過程,可得CLG 平滑約束的光流迭代公式:

將式(11)和(15)代入迭代式(31),計算v1和v2在第k步迭代的估計值.迭代收斂條件與第2.3.1節相同,經過多次迭代,最終得到連續稠密光流的估計結果.與Pan 等[39]方法不同的是,本文方法利用EDI 模型重建連續清晰亮度圖像的優勢,推導出同樣在時間上具有連續性的光流估計方法,因此在高速運動的極端場景下具有一定的優勢,而文獻[39]則基于曝光時間內光流恒定的假設,對亮度圖像進行去模糊操作.

算法1.基于事件相機的連續光流估計算法

3 實驗結果及分析

本文使用兩組數據集對算法進行測試.第1 組來自Bodo 等[31]提供的數據集,由DAVIS240 相機[18]錄制且帶有光流真實值.該數據集場景簡單,所有事件點均由相機低速運動生成.圖2 展示了該數據集中TranslBoxes、RotDisk 和TranslSin 三個數據的亮度圖像和對應事件幀,對應結果如圖3、圖4 所示.第2 組是運動模糊數據集,圖5(a)展示了該數據集中三個數據的亮度圖像,前兩行數據來自Pan等[38]提供的真實模糊事件數據集,第3 行數據為使用DAVIS346 相機錄制的真實模糊事件數據.第2組數據集包含高速運動導致亮度圖像模糊的更具挑戰性的情況,可以用于驗證本文算法在極端場景下的魯棒性,但不帶有光流真實值.在實驗中,將本文提出的引入HS 約束和CLG 約束的連續光流估計模型分別命名為EDI-HS 和EDI-CLG.

圖2 DAVIS240 數據集的亮度圖像和對應事件幀((a)TranslBoxes 數據;(b)RotDisk 數據;(c)TranslSin 數據)Fig.2 Brightness image and corresponding event frame of DAVIS240 datasets ((a)TranslBoxes dataset;(b)RotDisk dataset;(c)TranslSin dataset)

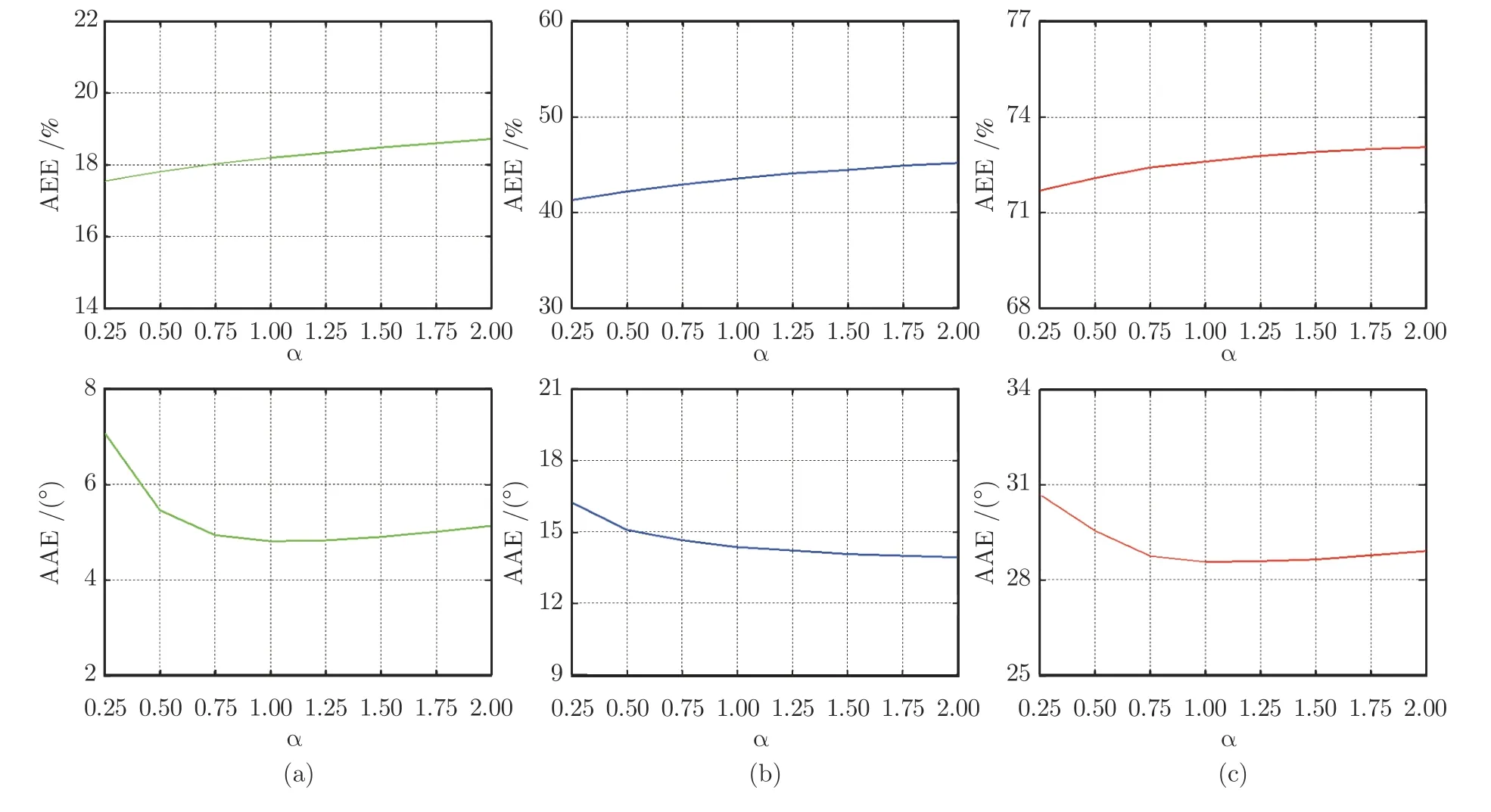
圖3 正則化參數 α 與光流誤差的關系曲線 ((a)TranslBoxes 數據;(b)RotDisk 數據;(c)TranslSin 數據)Fig.3 Relationship between optical flow error and regularization parameter α ((a)TranslBoxes dataset;(b)RotDisk dataset;(c)TranslSin dataset)

3.1 參數選取

算法1 中待設定的參數為平滑約束的正則化參數α.本文主要通過實驗方式對該參數進行設置,選擇帶有標準偏差的平均端點誤差(Average end point error,AEE)和平均角度誤差(Average angular error,AAE)以及均方誤差(Mean square error,MSE)來作為光流精度的衡量指標.AEE 表示光流大小與真實值的誤差,單位為%:

AAE 表示光流方向與真實值的誤差,單位為(°):

MSE 可用如下公式表示:

式中,vi=(vx,vy)i表示第i個光流測量值,ui=(ux,uy)i表示相應的光流真實值.

采用第1 組DAVIS240 數據集進行實驗,通過觀察不同的正則化參數對所計算光流的平均端點誤差和平均角度誤差的影響,對參數進行選取.在α取值為[0,3000]范圍內進行了大量實驗,通過實驗發現,在各數據集上,當α>2 時,兩種誤差都隨α的增大而升高,光流質量變差.因此,圖3 展示了α取值在區間[0,2]上對所得光流的平均端點誤差和平均角度誤差的影響曲線.可以發現,相較于平均角度誤差,平均端點誤差受參數α的影響更小且平均端點誤差隨α的增大而緩慢升高,平均角度誤差隨α的增大呈現先降低后升高趨勢.當α=0.75 左右時,可以同時保證兩種誤差均為較低,因此在后續實驗中設置α=0.75.

3.2 連續光流估計結果

為驗證本文算法的精度,將它們與現有的基于事件相機的光流估計算法進行比較,分別為Almatrafi 等[21]提出的聯合DVS 和APS 數據的光流估計方法、圖像對比度最大化光流估計法[15]和局部平面擬合光流估計法[16].將它們分別命名為DAVIS-OF、DVS-CM 和DVS-LP.其中,DAVIS-OF 光流估計算法在添加CLG 平滑約束時取得了最好的效果,因此本文在進行對比實驗時,也對其添加了CLG平滑約束.

首先,使用第1 組DAVIS240 數據集對算法進行實驗測試.表1 展示了各個算法在這3 個數據上的光流估計結果與真實值之間的誤差,精度排名第1 和第2 的算法分別使用加粗和下劃線標注.總體上,EDI-CLG 的結果最好,在3 個數據上的誤差都比較小,EDI-HS 在TranslBoxes 和TranslSin 兩個數據上的結果比另外3 種現有算法更優,且EDICLG 光流結果的標準差在3 個數據上都較小,說明EDI-CLG 的光流結果較為穩定,很少有異常值,具有良好的抗噪性能.實驗結果表明,在DAVIS-240 數據集上,本文算法相比于其他3 種對比算法,在精度和穩定性上具有一定優勢.

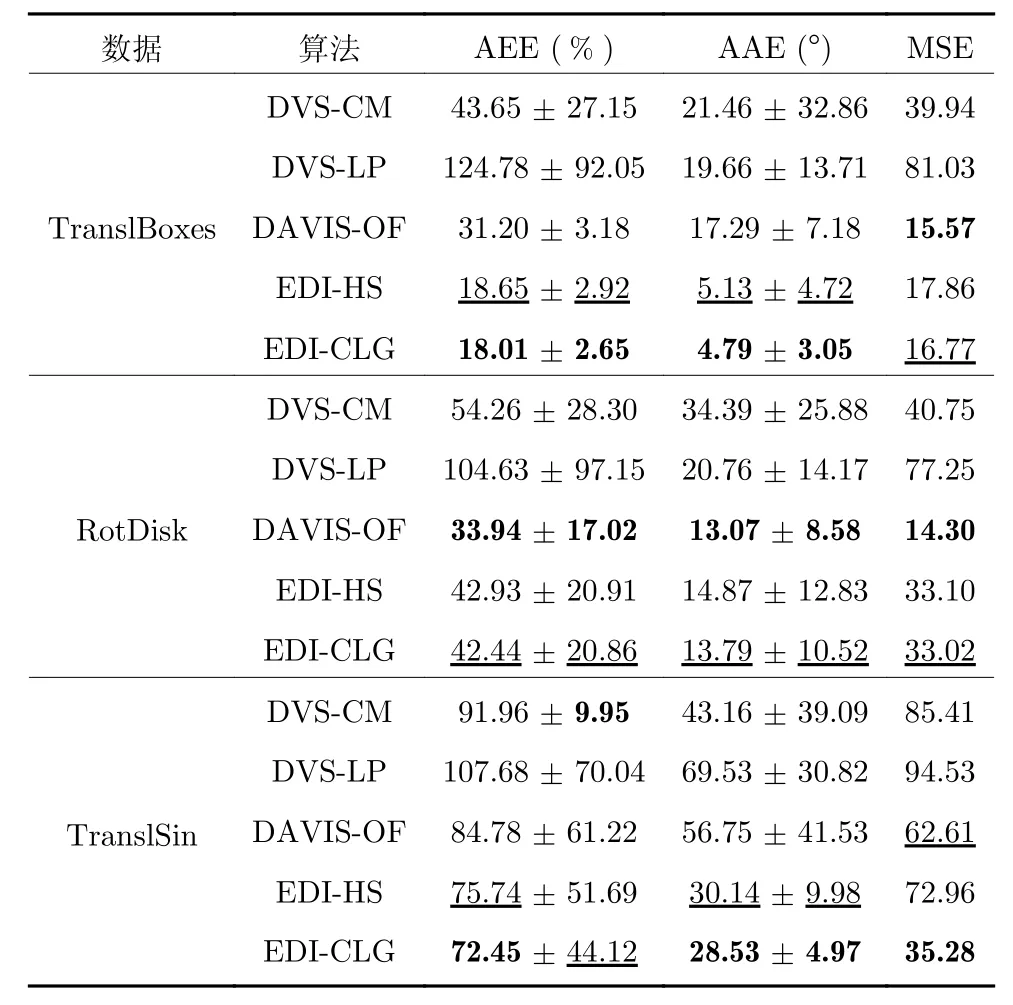
表1 DAVIS240 數據集光流誤差表Table 1 Optical flow error on DAVIS240 datasets

表2 展示了各個算法在3 個數據上的運行時間對比,其中運行速度排名第1 和第2 的算法分別使用加粗和下劃線標注.使用Matlab2014a 進行光流估計的平均每幀運行時間作為衡量指標,其中,DAVIS-OF 的運行時間最短,EDI-HS 的運行時間也相對較短,而EDI-CLG 的迭代過程相比于EDIHS 較為復雜,因此運行時間略長,DVS-CM 則由于逐像素迭代計算光流,平均每幀運行時間為最長.實驗結果表明,在DAVIS240 數據集上,本文算法的運行時間相比于現有算法具有一定的優勢.

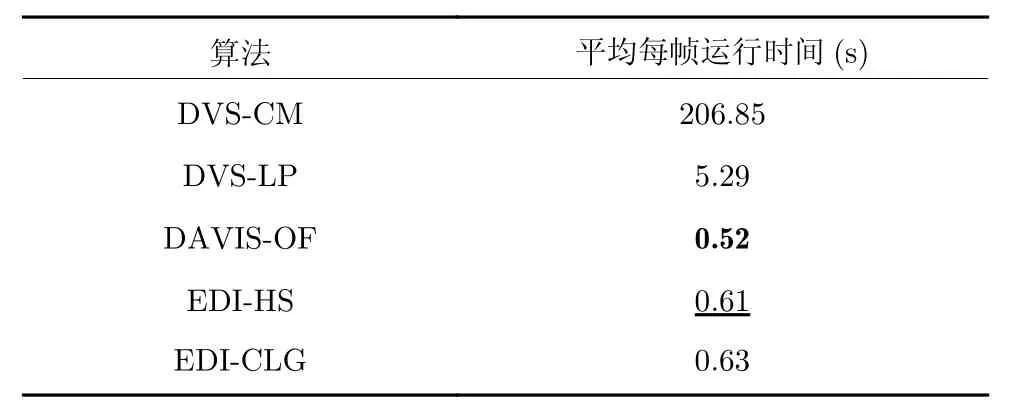
表2 運行時間對比Table 2 Comparison of running time

圖4 為利用第1 組數據集中TranslBoxes、Rot-Disk 和TranslSin 三個數據對本文的連續光流估計方法與其他3 種光流估計算法進行測試的結果對比圖.為便于可視化,對光流場進行了下采樣.圖4 包括光流真實值圖像以及5 種算法的光流結果圖.其中,綠色的直線箭頭表示光流,所有光流估計結果都在事件幀圖像上顯示.

在TranslBoxes 數據中,箱子在圖像上表現為向右移動,事件幀圖像中噪聲較少且邊緣明確.其中,EDI-CLG 的光流結果較好,大小和方向都最接近真實值;DAVIS-OF 的光流方向總體較好,但光流大小缺乏一致性.而DVS-CM 和DVS-LP 個別事件點的光流發生了明顯錯誤,特別是DVS-LP 有些光流值幅度很小,增加了AEE 誤差,結果見表1.在RotDisk 數據中,分隔成不同顏色區域的圓盤順時針轉動,從真實值上可以看出,光流方向基本都垂直于區域邊緣且光流大小與圓盤半徑成正比.其中,EDI-CLG 的光流比較穩定,并且光流大小基本符合與圓盤半徑的正比關系,這有效減少了光流誤差.而EDI-HS 的光流方向較好,但是某些邊緣上的光流大小比例不正確.DAVIS-OF 的光流大小最符合與圓盤半徑的正比關系,但有些地方輸出的光流方向不夠準確.DVS-CM 由于只對局部區域做對比度最大化,光流方向并不都垂直于邊緣;DVSLP 則有許多錯誤的光流方向,有些甚至與運動反向.在TranslSin 數據中,圖像表現為黑白正弦曲線向左移動,由于黑白邊界并不清晰,事件幀圖像上邊緣不明確且有許多噪點.其中,EDI-HS 和 EDICLG 估計的光流方向較為一致,但有個別光流幅值較大.而對比算法DAVIS-OF、DVS-CM 和DVSLP 輸出的光流方向不穩定,且大小也比較雜亂.

為了驗證本文算法在更具挑戰性的場景下進行光流估計的準確性和穩定性,下面使用第2 組運動模糊數據集進行測試.第2 組數據集提供了高速運動導致亮度圖像模糊的情況,可以用于驗證本文算法在極端場景下的魯棒性.

圖5 展示了各種算法在第2 組數據集上的測試結果,包括數據集中的模糊亮度圖像、使用EDI 方法重建的清晰亮度圖像和各個算法的光流結果圖.第1 行展示的數據是人手臂揮動黑白格圖像,第2行數據是人在室內起跳后落下,第3 行數據是高速移動的相機拍攝的棋盤格.由圖5 可以看出,在目標高速運動且亮度圖像存在運動模糊的情況下,本文提出的兩種連續光流估計算法都能穩定估計光流,光流方向都較為準確且變化較為平滑,其中EDI-CLG 估計的光流視覺效果最好,DVS-CM 和DVS-LP 的光流則存在異常值,方向準確度也不高.

3.3 連續光流的精度穩定性測試實驗

通過與基于傳統相機的光流估計算法對比可知,本文算法可以在一幀亮度圖像的曝光時間內進行多次光流的計算(見圖1),說明本文算法在時間上具有連續性.然而,當光流連續輸出時,仍需進一步測試其精度是否穩定.因此,將本文提出的EDICLG 算法與 DAVIS-OF 方法進行連續光流的穩定性對比實驗.

利用第1 組數據集中TranslBoxes 數據進行測試.最初使用算法1 得到的連續光流誤差表明,本文算法在每一幀圖像的曝光邊界時刻,光流質量會比曝光中間時刻明顯變差(見圖6(a)、圖6(b)).這是由于在亮度圖像的曝光邊界時刻,EDI 模型對模糊圖像的補償效果比在曝光中間時刻差[38],從而影響曝光邊界時刻重建圖像的質量,進而影響到光流估計的精度.因此,采用Niklaus 等[42]提出的亮度圖像插幀算法,將前面使用EDI 模型進行重建的連續清晰亮度圖像序列中每幀曝光邊界時刻生成的圖像,通過前后兩張圖像的插幀,替換為更高質量的重建圖像,使連續光流估計的精度得到了進一步提升.

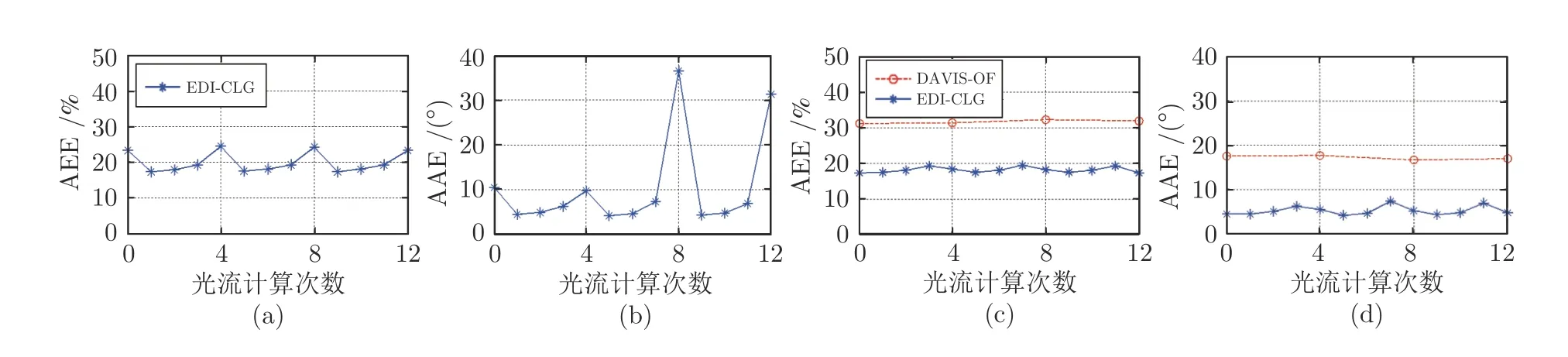
圖6 連續光流誤差對比折線圖 ((a)EDI-CLG 算法改進前的平均端點誤差;(b)EDI-CLG 算法改進前的平均角度誤差;(c)EDI-CLG 算法改進后與DAVIS-OF 算法的平均端點誤差對比;(d)EDI-CLG 算法改進后與DAVIS-OF 算法的平均角度誤差對比)Fig.6 Continuous optical flow error comparison ((a)The average endpoint error of EDI-CLG before improvement;(b)The average angular error of EDI-CLG before improvement;(c)Comparison of the average endpoint error between the improved EDI-CLG and DAVIS-OF;(d)Comparison of the average angular error between the improved EDI-CLG and DAVIS-OF)

圖6(c)、圖6(d)展示了2 種算法的光流估計結果與真實值之間的平均端點誤差和平均角度誤差對比折線圖,選擇數據集中連續3 幀圖像進行實驗,對本文方法進行每幀圖像曝光時間內連續4 次光流計算.由對比兩組光流的平均端點誤差和平均角度誤差結果可以看出,本文算法估計出的連續光流誤差更小且在多幀曝光時間內,可以保持精度的穩定性.

圖7 展示了單幀亮度圖像曝光時間內進行連續光流的精度穩定性測試的結果對比圖.其中,DAVISOF 算法只能估計建幀時刻的非連續光流,因此輸出單張光流結果(見圖7(b)).而本文提出的EDICLG 算法可以在單幀亮度圖像的曝光時間內多次計算光流(本文實驗計算4 次),如圖7(c)所示.可以看出,與對比算法相比,本文算法獲得的光流與真實值更加接近,而對比算法輸出的光流精度較低且有些事件點處沒有輸出光流.

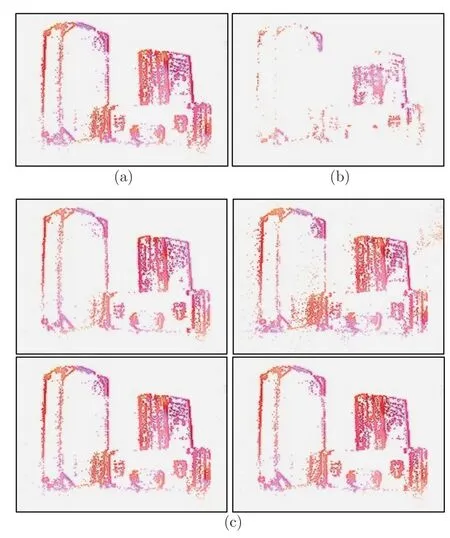
圖7 EDI-CLG 算法和DAVIS-OF 算法連續光流結果對比圖 ((a)光流真實值;(b)DAVIS-OF 方法;(c)本文EDI-CLG 方法在單幀圖像曝光時間內連續4 次進行光流計算的結果)Fig.7 Comparison of continuous optical flow results between EDI-CLG algorithm and DAVIS-OF algorithm((a)Ground truth;(b)The DAVIS-OF method;(c)The results of four continuous optical flow calculations within the exposure time of a frame using the proposed EDI-CLG method)

4 結束語

在相機或目標高速運動的極端場景下,由于相機自身較低的時間分辨率等局限性,基于傳統光學相機的光流估計方法難以估計出連續的光流結果.針對這一問題,本文提出基于事件相機的連續光流估計算法,該算法聯合了事件相機輸出的DVS 數據和APS 數據各自優勢,不僅能夠重建出任意時刻的清晰亮度圖像,而且可以保證光流估計的連續性和穩定性,解決了相機APS 數據易受運動模糊影響的問題.在計算光流時,本文通過引入兩種平滑約束來計算稠密光流,進一步提升了算法的魯棒性和準確性.實驗結果表明,本文算法相較于現有的光流估計算法,在平均端點誤差、平均角度誤差和均方誤差指標上,性能均有較大提升.在目標高速運動的極端場景下,也依然能夠有效且魯棒地估計連續光流.