基于分數布朗運動過程模型的混合隨機退化設備剩余壽命預測
高旭東 胡昌華 張建勛 杜黨波 喻 勇
隨著科學技術的不斷進步與發展,在實際工程中,設備內部結構的復雜性、運行載荷和外部環境的多變性也隨之不斷增加,導致設備的退化過程通常具有隨機性、階段性、多樣性、相關性和混合性等特征[1-2],這給設備的健康管理帶來了一定的難度和挑戰.為了避免由于退化失效而造成人員與財產損失,有必要研究該類設備的退化建模與剩余壽命(Remaining useful life,RUL)預測問題,進而保障其安全、可靠運行.但是,如何準確預測此類隨機退化設備的剩余壽命仍是目前研究的難點與熱點問題.
在實際工程中,常常會遇到混合退化過程的設備[1-2],但現有文獻處理方法是將設備的退化過程簡化成單一的線性或非線性Wiener 過程[3-9],可以比較容易得到設備RUL 的解析解.例如對于具有線性擴散項的維納退化過程,Si 等[3]研究了三層不確定因素影響下線性隨機退化系統的RUL 預測方法;Huang 等[4]在文獻[3]基礎上,提出一種帶自適應漂移系數的隱線性Wiener 模型,用以描述設備的退化軌跡,引入自適應漂移參數及測量噪聲,同時考慮設備歷史數據及測量噪聲問題,進一步提高了設備RUL 的預測精度;王璽等[5]基于線性Wiener 過程,針對新研發光電產品提出一種剩余壽命自適應預測方法,克服了現有RUL 預測方法中,當前時刻估計的隨機參數與上一時刻隨機參數的后驗估計完全相等的潛在假設,進而提高了RUL 的預測準確性.
對于具有非線性擴散項的Wiener 退化過程,Si 等[6]使用時空變換方法,獲得了RUL 的近似解析解.司小勝等[7]考慮了退化過程中的測量不確定性,然后根據維納過程的統計性質,建立一個狀態空間模型預測RUL,但是RUL 的分布中未考慮測量不確定性.鄭建飛等[8]在文獻[7]基礎上,還考慮了個體差異的不確定性,并在RUL 分布的推導中考慮了測量不確定性和個體差異性,進一步提高了RUL的預測精度.Cai 等[9]考慮了退化量與監測量之間的非線性關系,推導得到了其RUL 的概率密度函數(Probability density function,PDF),且通過激光器數據驗證了該方法能夠明顯提高預測精度并降低預測結果的不確定性.
但是,這些退化過程都有兩個潛在的假設: 1)假設設備的退化過程是一種單一的線性或非線性退化形式,忽略了各種退化形式在整個退化過程所占的比重是不同的,影響效果是有差別的;2)假設設備的退化過程是一種無記憶效應馬爾科夫過程,忽略了監測數據之間可能存在的長期依賴性和相關性對RUL 的預測具有一定的影響.例如在發動機引擎性能退化數據[10]、高爐的性能退化數據[11-12]、鋰電池的性能退化數據[13]等數據中發現了記憶效應,即未來退化狀態受到當前狀態與歷史狀態的共同影響.文獻[14]在分數布朗運動(Fractional Brownian motion,FBM)的框架下,建立了設備的退化模型,使用復雜弱收斂定理將FBM 近似為標準布朗運動(Brownian motion,BM),然后推導了RUL 的PDF.文獻[15]建立了考慮退化狀態之間存在相關性的新型退化模型,并將其應用于高爐與發動機性能退化數據中,通過求取RUL 數值PDF 的方式驗證了此方法的有效性和優越性.文獻[16]在文獻[15]基礎上,使用更為簡單的弱收斂理論推導了RUL的近似PDF,避免大量的數值積分,同時考慮隨機效應的影響,并通過鋰電池性能退化數據進行驗證,驗證結果表明,該方法能夠有效提高RUL 的預測精度.但是,現有基于FBM 過程模型的設備RUL預測方法最大的不足是均未實時更新模型中的相關參數,僅利用同批設備的歷史退化數據對模型中的未知參數進行估計.此外,文獻[15]從結構組成和退化機理兩個方面分析了慣性導航陀螺儀的隨機退化過程具有混合性特征.相比于傳統單一退化形式的Wiener 過程對設備的隨機退化過程建模,通過建立混合隨機退化模型,能夠進一步提高RUL 預測精度.文獻[15]詳細論述和證明了考慮退化過程的混合性,能夠提高設備RUL 的預測精度.
鑒于此,本文將重點研究在記憶效應影響下同時包含線性退化過程和非線性退化過程的混合隨機退化設備建模與RUL 預測問題.主要關注以下3個問題: 1)如何建立存在記憶效應的混合退化過程模型;2)如何在首達時間(First hitting time,FHT)條件下,推導設備RUL 的解析表達形式;3)如何根據監測數據實時更新退化模型參數,并實現RUL分布的自適應更新.針對以上3 個問題,本文首先建立了一種基于分數布朗運動的混合退化模型,考慮了記憶效應對未來退化過程的影響;進一步,在弱收斂性理論和FHT 的概念下,推導了混合退化設備RUL 的近似解析表達式;然后,利用共性參數離線估計和隨機參數自適應更新的策略,實現RUL的自適應預測;最后,將本文方法應用于數值仿真例子和陀螺儀的監測數據上進行驗證.
1 基于FBM 的混合隨機退化模型
首先,令X(t)表示混合退化設備在t時刻的退化量.基于上文的具體分析,受記憶效應影響的混合退化設備模型由以下3 部分組成[15]: 1)線性退化元件引起的線性退化過程;2)非線性退化元件引起的非線性退化過程;3)含有記憶效應的隨機波動.因此,在文獻[11]基礎上,在t時刻,基于FBM 混合退化模型可以表示為:
式中,X(0)表示混合退化設備的初始退化狀態,為了不失一般性,假設X(0)=0 (在實際中,若X(0)≠0,可以通過平移手段將其轉化為零[16-17]).λt代表混合退化設備的線性趨勢代表非線性退化趨勢;令λ和α為隨機變量,用于描述由結構差異、外部環境等差異引起的同批設備中不同個體差異性.β和σ是共性參數,用于反映同批設備的共同特性[18-19].為了刻畫線性退化部分與非線性退化部分之間的相關性,本文假設λ和α服從二維正態分布.另外,BH(t)為分數布朗運動,描述了退化過程中帶有記憶效應的隨機波動性.
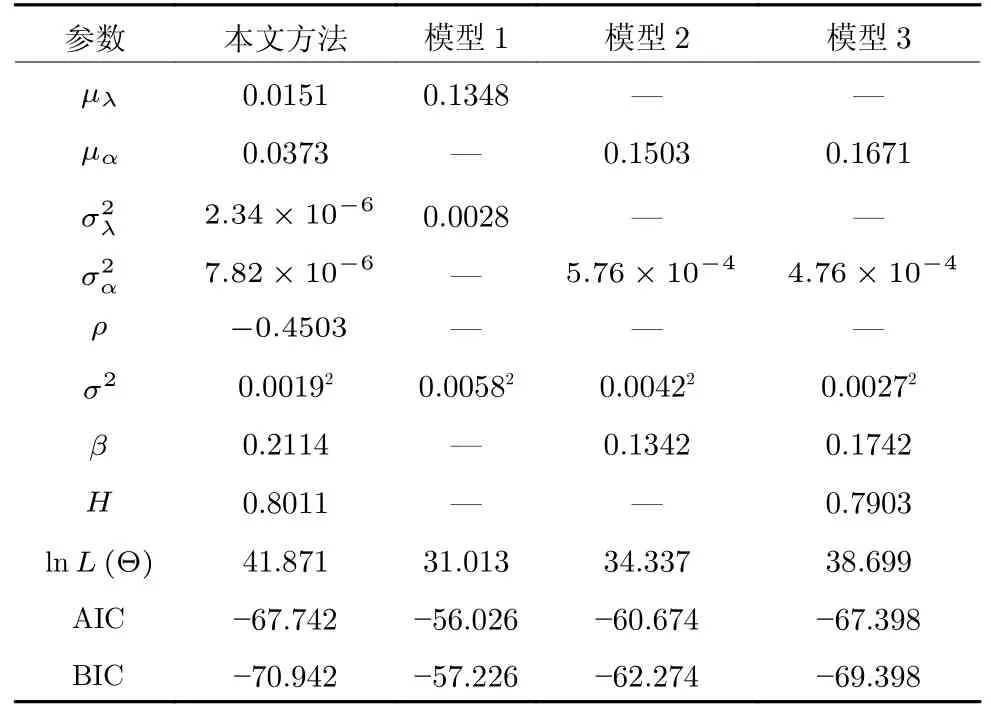
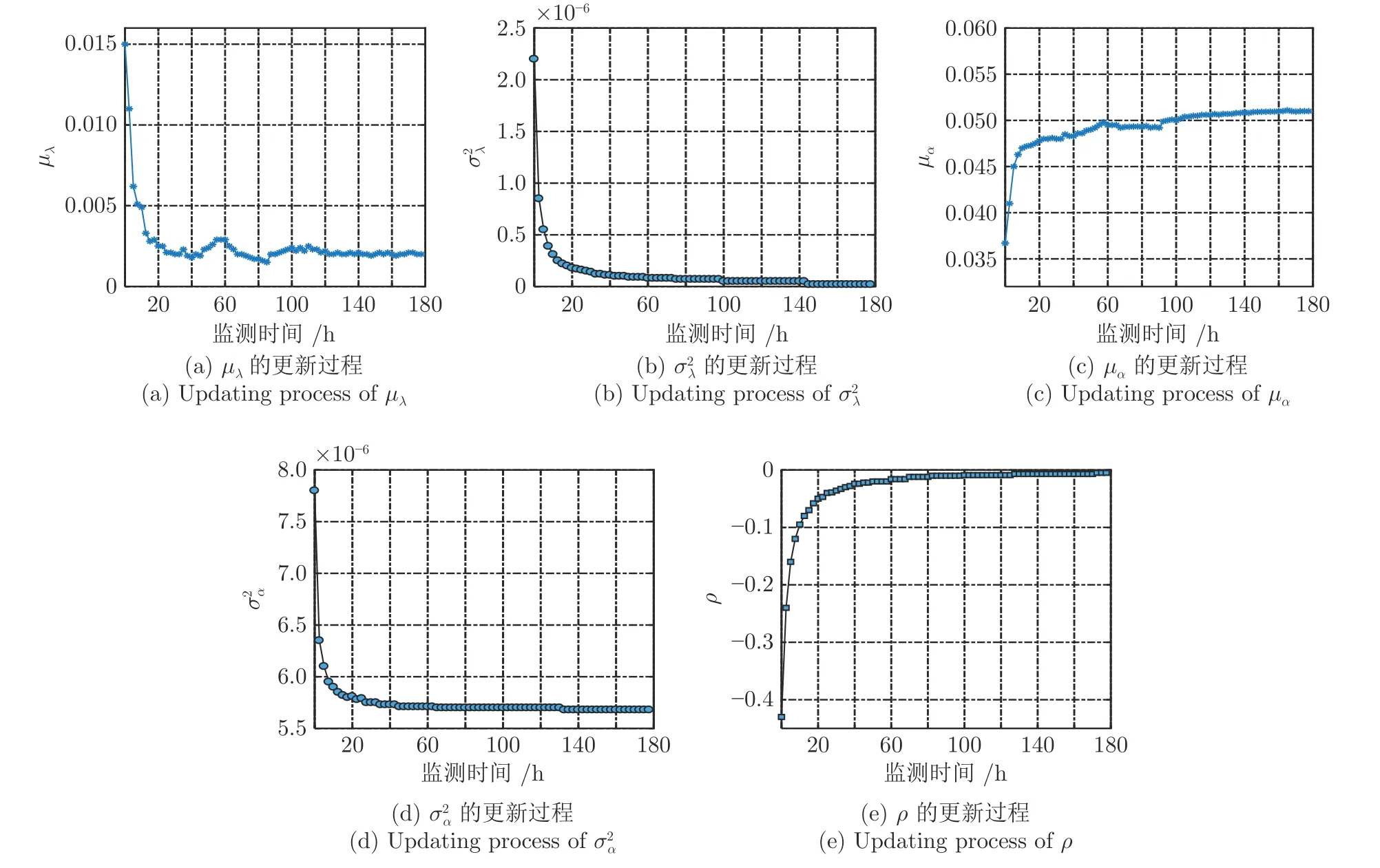
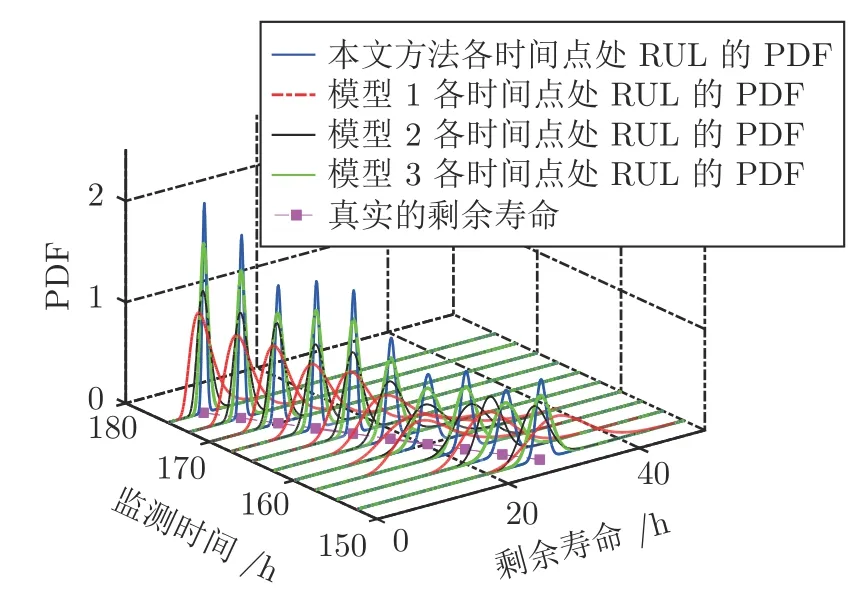
定義 1[13,20]. 赫斯特指數H的取值區間滿足0 的中心化高斯過程[21]: 式中,KH(t-s)定義為: Γ(·)為伽馬函數,具體形式為: 由式(3)可以看出,FBM 是BM 增量的非線性移動平均值[20],這進一步引入了記憶效應,其中: 為了簡化σB的計算,假設式(1)中的BH(t)為標準FBM[13].標準FBM 滿足[21]: 1)BH(0)=0 且 E (BH(0))=0; 2)?t≥0,E(BH(t)2)=t2H; 3)分數布朗運動具有自相似性和平穩增量; 4)分數布朗運動的樣本軌道是連續但幾乎不可微的; 5)當 1/2 因此對于任意的λ∈R,α∈R,σ∈R當且僅當 1/2 注1.FBM 是一種具有長期依賴性、自相關性的連續非馬爾科夫過程[20],其增量是固定且相關的,并且引入了長程相關的結構[22-23].赫斯特指數H可以測量整個退化軌跡之間的長期依賴性.根據H的不同,FBM 可以分為三種類型,當 0 基于FHT 的定義[25],當失效閾值為ω時,目標設備在任意時間tk的剩余壽命Lk定義如下: 基于式(1)、式(7)和弱收斂理論[26]推導得到目標設備RUL 的近似PDF,如定理1 所述.定理1 考慮了關于FBM 的更簡單的弱收斂方案,提出了基于FBM 過程的混合退化模型的RUL 分布. 式中,ωm,k=ωm-xm(tk),=h(tk+lk)-h(tk),=h(tk+lk+?l)-h(tk+lk). 定理1 的證明見附錄A. 下面對混合退化模型中的未知參數進行實時估計更新,從而實現混合退化設備RUL 的自適應預測. 式中,λ0與α0分別表示隨機參數λ和α的先驗值,將其聯合先驗分布記作π0~ρ0). 為了方便推導,令: 假設同批次不同設備個體之間的歷史退化數據都是互不相關的.因此,對第m個隨機退化設備的所有歷史監測數據可以進一步寫為: 定理2.Xm的聯合分布為多元正態分布,其均值與方差如下: 定理2 證明見附錄B. 根據定理2 可以得到模型參數 Θ 的似然函數如下: 式(19)對μλ0和μα0分別求一階偏導,可得: 將式(22)、式(23)代入式(19),可得: 可以看出,似然函數(24)具有高維的特征,直接把式(24)極大似然化很難得到其余參數的極大估計值.本文首先利用Matlab 中的fminsearch 函數,求取極大似然估計值(該函數基于Nelder-Mead 單純形法對最小化執行同步多維搜索),進而得到參數的估計值;然后,將其代入式(22)、式(23),得到相應μλ0、μα0的極大似然估計值;最后,采用貝葉斯推理方法,利用設備的實時退化監測數據對隨機參數進行實時更新. 第3.1 節通過參數離線估計的方法得到了隨機參數λ和α的聯合先驗分布,下面對隨機參數進行實時更新.假設第m個設備在前tk時刻一共獲得k個退化監測數據Xk?,記作: 式中,ti(i=1,2,···,k)表示對應的退化監測時刻. 基于貝葉斯推理理論,利用獲得的退化數據更新λ和α的聯合后驗分布,即: 將估計得到的聯合分布π0(λ,α)、式(27)代入式(26),對λ和α的聯合后驗分布進行更新,具體更新結果如下: 基于式(29)、式(30),λ和α在tk時刻聯合后驗分布中的相關參數可以由下式得到: 將第3.1 節參數的離線估計與第3.2 節參數的實時更新歸結為算法1.至此,完成了模型里面隨機參數的實時更新.下面將本文方法應用到數值仿真和陀螺儀實際退化監測數據中. 算法1.參數的離線估計與實時更新算法 本節將本文所提方法應用到數值例子與實際例子中,驗證其是否有效.采用線性退化模型、非線性退化模型和本文提出的模型來擬合退化數據,并且比較在三種模型下設備RUL 的預測結果.三種模型為: 1)本文設計的模型;2)模型1.基于帶線性漂移 的Wiener 過程模型[5];3)模型2.基于帶非線性漂移的Wiener 過程模型[8,27];4)模型3.基于帶非線性漂移的FBM 過程模型(單一退化形式)[13-14](未考慮隨機系數的實時更新). 1)仿真數據 圖1 30 組仿真歷史退化數據Fig.1 30 sets of simulated history degradation data 圖1 是30 組仿真退化軌跡,仿真監測時間為0~15 s,采樣間隔為0.1 s,每條軌跡共150 個采樣點.圖2 為其中任意一條退化軌跡.作為帶預測設備的實時監測數據,為了簡單化,將該軌跡的最后一個監測數據X(15)=13.1 作為失效閾值,即ω=13.1.則該設備的剩余壽命可近似為14.8 s. 圖2 待預測設備實時監測退化數據Fig.2 Real-time monitoring degradation data of the equipment for prediction 下面利用圖2 的仿真退化數據對本文所提模型和RUL 預測的有效性進行驗證. 2)結果對比 為了比較的公平性,模型2、模型3 中的非線性部分也采用冪函數的形式.首先,基于歷史退化數據,采用極大似然估計算法得到共性參數與隨機參數的先驗估計值.為了對比度量四種模型之間的擬合的精準度與估計的準確度,使用赤池信息準則(Akashi information criterion,AIC)[28]、貝葉斯信息準則(Bayesian information criterion,BIC)[29]測量預測模型的擬合程度.AIC、BIC 的值越小,則擬合程度越高;反之,則擬合越差.AIC 的具體公式為: 式中,L(Θ)表示似然函數值,p是未知參數的總個數. BIC 引入了改進懲罰項,懲罰項大于AIC 的,可以有效避免大樣本的過擬合問題,其具體表達式為: 式中,L(Θ)表示似然函數值,p是未知參數的總個數,n為樣本數據量. 表1 為四種模型參數(本文方法、模型1、模型2、模型3)的先驗估計值. 表1 四種模型參數的先驗估計值Table 1 The parameters' prior estimates of the four models 由表1 可知,本文方法的AIC 與BIC 值最小,并且其中的3 個方差參數總體也比較小,這說明本文模型參數估計的準確性更高.主要原因是本文所提模型既考慮退化過程的混合性,還考慮了退化狀態之間可能存在的相關性. 得到參數的離線估計值后,基于待預測設備的實時監測退化數據,采用貝葉斯更新的方法實現λ和α的實時更新,進而實現RUL 的實時預測.圖3是本文模型中λ和α的實時更新過程. 圖3 隨機參數的實時更新過程Fig.3 Real-time updating process of random parameters 由圖3 可以看出: 1)隨著仿真退化數據的不斷獲取,隨機參數不斷實時更新;2)ρ的實時更新值為負,表明λ和α是負相關,進一步表明混合隨機退化設備的線性退化部分與非線性退化部分是相互抑制的. 下面對比在四種方法下得到的RUL 實時預測結果.預測時間點共取10 個,從第5 個時間點(第50 個采樣點)到第14 個時間點(第140 個采樣點),間隔為10 個采樣點,具體RUL 對比見圖4.同時選取第5、8、11、13 個時間點的RUL 預測結果,通過二維平面圖形式做進一步對比,對比圖如圖5所示. 圖4 4 種方法在各個時間點處RUL 預測的對比Fig.4 Comparison of RUL prediction by four methods at each time 圖5 四種方法在第5、8、11、13 個時間點RUL 預測結果的對比Fig.5 Comparison of RUL prediction by four methods at 5,8,11,13th time 在圖4 和圖5 中,藍色曲線為本文方法RUL的PDF,紅色曲線為模型1 得到的PDF,黑色曲線為模型2 得到的PDF,綠色曲線為模型3 得到的PDF.可以看出: 1)四種模型隨著獲取的退化數據增多,RUL 預測的精度越來越高;2)本文方法得到的RUL 的PDF 能夠更好地覆蓋真實的RUL,其預測均值更接近真實的RUL,較模型1、模型2、模型3 得到的PDF 精度更高;3)本文方法預測得到的RUL 的PDF 更為尖銳和緊湊,這說明本文方法預測的不確定性比其他三種方法預測的不確定性更小.由圖4、圖5 可以直觀地看出,本文方法優于其他三種方法. 下面從定量的角度分析四種方法的優劣.使用均方誤差(Mean squared error,MSE)指標來評價四種方法預測RUL 的精度,其既可以表征RUL 預測結果的準確性,還可以表征RUL 預測的不確定性,是常用的誤差評定指標,可以較好地對比不同預測方法的優劣.待測設備在tk的RUL 的MSE 可以表示為: 所有預測時間點處的均方誤差之和為總體均方誤差(Total mean squared error,TMSE).很明顯,TMSE 值越小,則該方法的RUL 預測精度就越高.通過計算得到四種方法在第10 個時間點處的TMSE分 別為1.0051 × 102、5.1308× 103、1.1007×103、1.5041 × 102.通過對比可知,本文方法的RUL 預測精度高于傳統模型1、模型2、模型3 的RUL 預測精度;相比于模型1 和模型2,精度約提高了一個數量級.定量分析結果與圖4、圖5 直觀得到的結論是一致的. 陀螺儀是慣性導航系統、導彈制導與控制系統的關鍵設備,決定著導彈導航與命中的精度.但是,隨著陀螺儀工作年限的增加,在外部復雜環境與內部隨機應力的影響下,陀螺儀的性能可能會隨之發生退化,主要表現在其漂移系數的不斷增大,如果漂移系數值增大到一定程度,陀螺儀就無法正常工作,即陀螺儀發生失效. 本文獲取的5 組某型號陀螺儀的退化監測數據[30],每組73 個數據,采樣間隔為2.5 h,陀螺儀失效閾值設定為0.37 (°/h),陀螺儀壽命約為180.5 h.首先,基于極大似然估計算法,利用其中4 組退化數據[30]對模型參數進行離線估計,得到其先驗估計值;其次,利用剩下一組數據為待預測的陀螺儀的實時監測數據,采用貝葉斯更新的方法,對模型隨機參數進行實時更新;最后,進行設備RUL 的實時預測,并且將模型1、模型2、模型3 得到的RUL 進行比較.圖6 為待預測陀螺儀的實時監測數據. 圖6 待預測陀螺儀漂移數據Fig.6 Drift data of the gyroscope for prediction 為了比較公平,模型2、模型3 中的非線性形式和本文模型的非線性部分都采用冪函數形式.調用算法1 中的離線估計階段得到模型參數的先驗估計值,如表2 所示. 表2 陀螺儀退化模型參數的先驗估計值Table 2 A parameters' prior estimate of the gyroscope degradation model 下面基于陀螺儀模型參數的先驗估計值,調用算法1 中的參數實時更新階段,在每一個時間點對模型隨機參數進行實時更新,模型隨機參數的實時更新過程如圖7 所示.由圖7 可知,隨著陀螺儀監測數據獲取的增加,模型中隨機參數不斷實時更新,并趨于穩定狀態,這表明隨機參數的估計值越來越接近真實的模型參數值. 圖7 陀螺儀退化模型隨機參數的實時更新過程Fig.7 Real-time updating process of random parameters of gyroscope degradation model 下面選擇第152.5 h~175 h 之間的10 個時間點為例,比較分析所使用四種方法對該型號陀螺儀RUL 預測的精準程度.在所選的10 個時間點,四種方法預測該型號陀螺儀RUL 的PDF 如圖8 所示.由圖8 可知: 1)四種方法預測得到RUL 的PDF在10 個時間點都能夠比較好地覆蓋真實的RUL,說明了四種方法能夠有效地預測該型號陀螺儀的RUL.2)隨著監測數據的增加,參數不斷實時更新,四種方法預測RUL 的PDF 隨著時間變得越來越尖、越來越窄,說明四種方法對RUL 預測的不確定度隨著監測數據的累積而不斷減小.3)本文方法得到RUL 的PDF 與其他三種方法相比較,其RUL的PDF 明顯更高、更緊致,說明本文方法預測得到的RUL 更準確,并且預測的不確定度更小.其原因是,相比于模型1 和模型2 單一的馬爾科夫建模方式,本文方法不僅考慮了陀螺儀內部不同類型的隨機退化過程,還考慮了退化監測數據之間的長期相關性、記憶性,克服了模型1 和模型2 中的強馬爾科夫限制.相比于模型3,本文方法考慮了設備的退化混合性,更符合設備真實的退化過程. 圖8 在不同時間點處四種方法預測RUL 的PDF 對比Fig.8 Comparison of RUL's PDFs by four prediction methods at each time 進一步通過計算,得到四種方法在10 個時間點的TMSE 分別為 1.8154×102、2.6321×102、3.6543×102、2.1031×102.可知,本文方法的RUL 預測精度高于其他三種方法. 本文針對隨機退化設備,提出一種考慮隨機退化過程中退化狀態之間可能存在長期相關性、記憶性特點的混合隨機退化模型,克服了目前研究中潛在的假設: 1)假設設備的隨機退化過程為單一的線性或非線性形式,忽略了設備內部的多種類型退化過程分別對RUL 預測的影響;2)將設備的隨機退化過程簡化成無記憶效應的馬爾科夫過程,受到強馬爾科夫性的限制.最后,通過本文方法實現了隨機退化設備的RUL 壽命自適應預測,且預測精度高于同等條件下傳統模型的預測精度.主要結論有一下3 點: 1)基于FBM 的混合隨機退化模型,能夠更為準確、合理地描述設備隨機退化過程中可能含有的記憶效應.通過實例驗證和與傳統的建模方法比較,其RUL 預測結果更加精確、不確定性更小; 2)本文采用的參數估計方法有效地利用了設備的歷史退化信息和實時監測信息,從而更加準確地實現了設備RUL 的實時預測. 綜上所述,本文提出的基于FBM 的混合隨機退化模型對隨機退化設備建模更為合理與準確,并且RUL 預測結果優于傳統方法,具有一定的工程實用價值.下一步的研究方向為如何對預測模型中共性參數進行自適應更新. 附錄A 定理1 的證明 基于弱收斂理論,可以將模型(1)轉換成式(37).文獻[27]指出,時間重新縮放的FBM 保持零均值高斯過程,然后在適當的假設下給出了相應RUL 分布的近似表達式[13].具體來說,考慮以下退化模型: 假設失效閾值為ω,則第m個設備在tk時刻RUL 的PDF 如下: 定理1 的具體使用方法見文獻[13]. 附錄B 定理2 的證明 根據式(14),可得: 將式(B4)、式(B5)代入式(B3),可得:2 基于混合隨機退化模型的RUL 預測
3 隨機混合退化模型的參數估計
3.1 共性參數與隨機參數的離線估計
3.2 隨機參數的實時更新
4 數值仿真與實例驗證
4.1 數值仿真
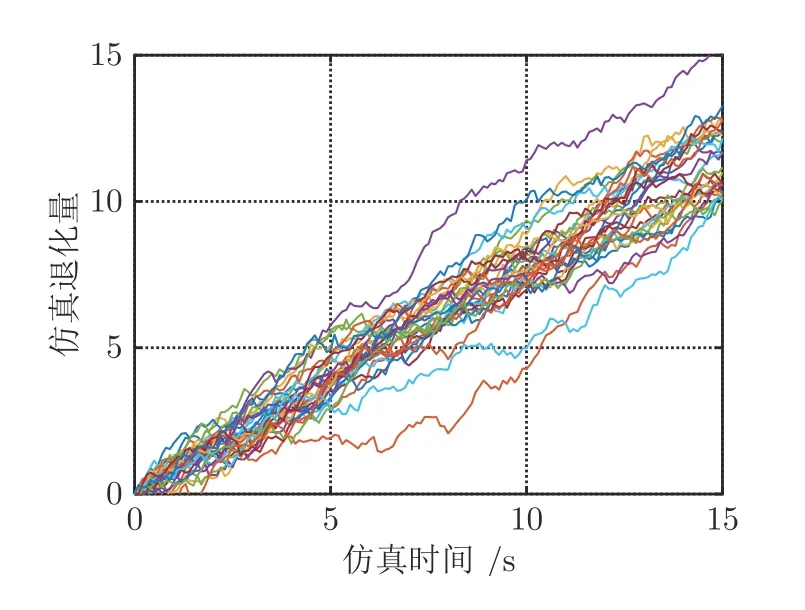
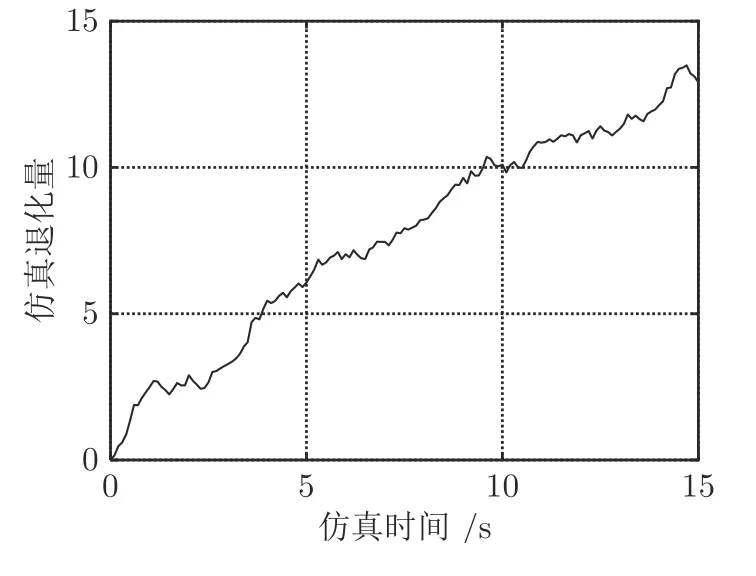
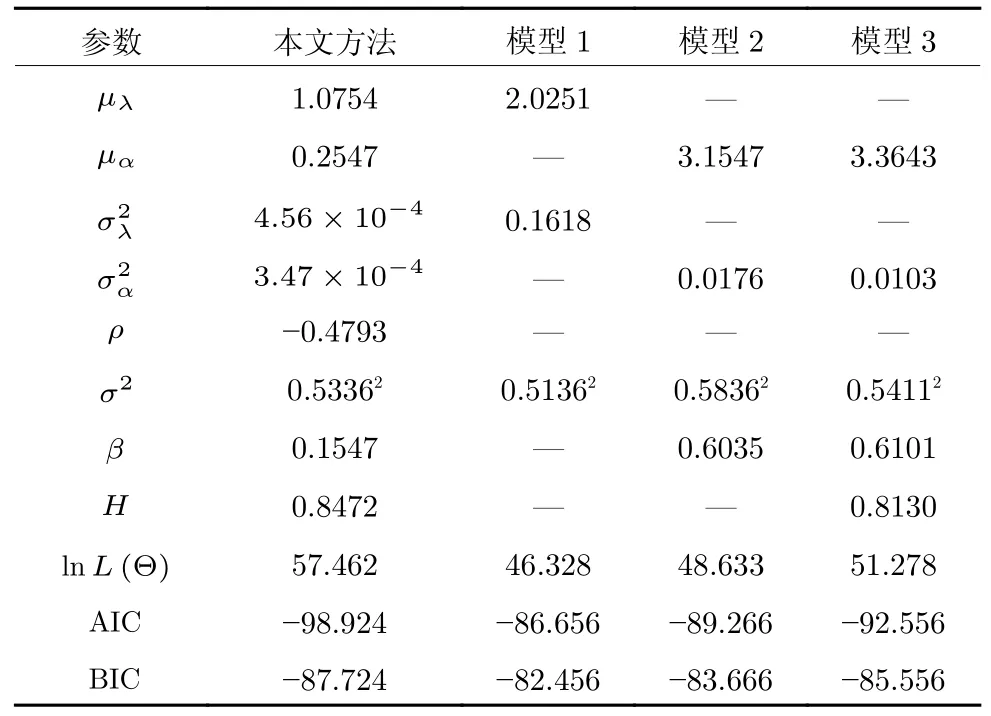
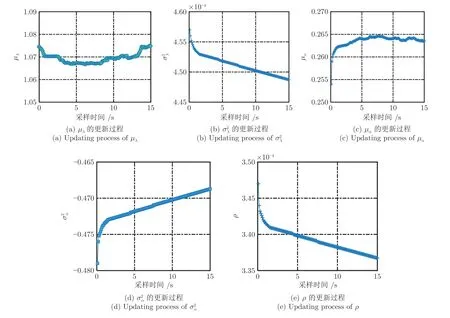
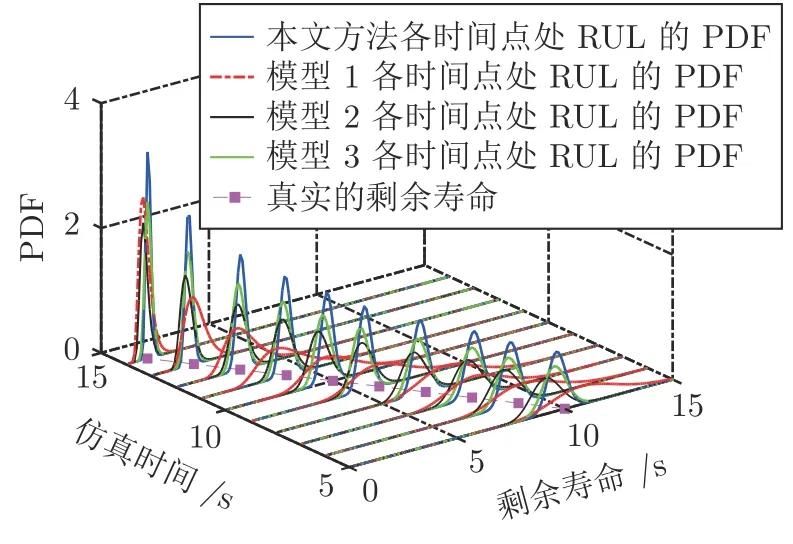

4.2 實例驗證

5 結束語

