雙貯備系統冷/溫/熱貯備模型的優化選擇研究

金海波 趙欣越 桑 雨

高可靠控制系統在現代工業的諸多領域中越來越重要,如航空航天、化工、核能、武器、生產制造等領域[1-3].實現控制系統高可靠性的一個主要手段是采用貯備技術.目前,對于一些先進生產制造企業,具有雙貯備設備的控制系統已逐漸涌現并凸顯其作用[4].因此,對這些雙貯備系統的可靠性和經濟性等指標進行定量分析和優化具有重要的理論意義和實際價值.

貯備系統按照貯備設備在系統運行時是否失效通常分為: 冷貯備系統、熱貯備系統和溫貯備系統[5-6].冷貯備系統是指系統運行過程中,貯備設備不參與工作也不老化.對能耗要求極高的系統往往配成冷貯備系統,如冶金系統、武器系統等[7].熱貯備系統是指運行設備和貯備設備在相同的環境下工作,因此兩種設備的失效率相同.熱貯備系統主要是對系統切換時間要求極高的系統,如網絡打印機、飛機引擎等系統[8-9].溫貯備系統是指貯備設備在系統工作期間參與工作,但在溫和的環境中工作其失效率小于運行設備.對需要平衡切換時間和能耗的系統大都配成溫貯備系統,如電力系統、存儲系統、高性能計算系統和飛機控制系統等[10-13].

由于三種貯備系統在不同應用領域中都有重要的作用,因此學者們對每種貯備系統在故障檢測、失效分析、可靠性分析、冗余分配及優化維修等方面都做了深入研究并取得了一定研究成果[14-15].在冷貯備系統研究方面,Chen 等[16]對兩部件冷貯備系統在不同失效機理的累積作用下進行了可靠性分析.分析過程中作者考慮了部件工作狀態和貯備狀態之間的依賴關系,評估了系統在不同失效機理影響下的動態演化過程,計算了不同階段應力持續影響下的部件損壞程度,最后建立了基于改進的序列二值決策圖方法的系統可靠性模型.Zhong 等[17]對雙設備組成的冷貯備控制系統提出了基于半Markov理論的最優預防維護策略.所提策略中作者使用再生點技術和半Markov 過程刻畫了系統狀態轉移概率并用Markov 更新理論建立了系統每個狀態逗留時間分布的線性方程組,最后以最大化系統壽命為目標,優化了系統最優維護周期.Wang 等[18]研究了由雙設備組成的冷貯備系統的更換策略,首先假設系統惡化過程服從廣義Polya 過程,在此假設下,作者以最小化系統長期平均費用率(Cost rate)為目標函數,給出了系統的最優更換策略.陳童等[19]針對裝備系統中多狀態工作部件存在退化失效與突發失效競爭的情況,以冷貯備系統為研究對象,研究隨機檢測策略.其中工作部件在各性能水平停留時間、各類維修時間等隨機時間變量以及外部沖擊的到達過程均采用相位型 (Phase-type,PH)分布進行描述.在此基礎上,建立了多狀態冷貯備系統可靠性模型,得到了系統可靠性主要參數的解析表達式.在熱貯備系統研究方面,研究成果相對較少,原因在于熱貯備系統中的工作設備和貯備設備失效率相同且以并聯方式工作.因此熱貯備的可靠性可完全借鑒并聯系統的可靠性方法進行分析.曹晉華等[20]利用Markov 更新過程和交替更新過程研究了兩個不同部件組成的熱貯備系統,推導了系統首次失效時間與其后停工時間的聯合分布、修理工在任一時刻忙的概率以及在(0,t]內系統失效率的分布及其均值等性能指標.Patowary 等[21]采用Markov模型結合故障樹分析(Fault tree analysis,FTA)方法研究了熱貯備微電網系統的可靠性,所提方法與傳統Markov 和FTA 方法相比能夠適應不同的系統失效率.與冷貯備系統相比,溫貯備系統中的貯備設備在貯備期間也逐漸惡化存在失效風險,但失效風險小于熱貯備系統.從貯備設備失效率角度看,冷貯備和熱貯備屬于溫貯備的兩個特例.因此溫貯備模型是更為一般的貯備模型,這也導致溫貯備系統的可靠性分析難度急劇增加.在溫貯備系統研究方面,近年來涌現出許多重要成果.Huang 等[22]以衛星數據處理子系統為背景,研究了一類特殊結構的溫貯備系統,該類系統由兩組相同數量的不同部件組成,一組是工作部件,另一組是溫備份部件.兩組部件分別由兩個電源供電.對這類貯備系統,作者給出了系統可靠度模型,建立了各個部件可靠度的閉合方程組,推導了系統可靠度的解析解.然而,該研究成果局限于各部件壽命都符合指數分布的情況,對其他壽命分布不再適用.Ma 等[23]研究了兩部件溫貯備冷卻系統,采用多階段維納過程刻畫系統惡化趨勢,提出了基于溫度檢測數據的優化維護模型.該模型中,同時考慮穩態溫度控制和系統壽命閾值,優化系統整體維護費用.尹東亮等[24]對具有維修和保養兩類活動的多狀態溫貯備系統進行了研究,考慮了維修較保養具有更高優先級的情況.用PH 分布構建了系統狀態轉移矩陣,推導了系統穩態可用度、系統故障率、平均故障間隔時間等可靠性指標.劉寶亮等[25]研究了修理設備和開關不完全可靠情形下的溫貯備可修系統,用補充變量法和Laplace 變換相結合的方式推導了系統瞬時可用度.該成果實際上是Kuo 等[26]研究成果的進一步擴展.

由此可見,關于三種類型貯備系統的可靠性問題學者們做了大量研究,同時取得了許多重要成果.然而這些成果大多是針對“用一備一”的情況進行研究.隨著某些尖端系統對高可靠性的要求,“用一備二”的情形逐漸涌現.對該類系統的研究也剛剛起步,其研究成果也鮮有報道.目前,我國某自動化廠商已經開始研發具有雙貯備設備(即“用一備二”)的控制系統,對該種控制系統配成冷/溫/熱三種模型中的何種模型是研發過程中需要解決的關鍵問題之一,具有現實意義.原因在于最優貯備模型可以提高系統穩態可用度(即可靠性),降低維修人員忙期穩態概率以及系統穩態平均維修次數,延長系統壽命.除此之外,在經濟方面最優貯備模型還能降低系統維修費用,提高系統單位時間內產生的效益.然而據作者查閱大量相關文獻可知,目前關于雙貯備系統的最優貯備模型選擇方面研究甚少,沒有可借鑒的通用方法.因此如何建立系統三種貯備模型并給出確定不同條件下最優貯備模型的優化選擇算法是主要研究難點.為此,本文用Markov 及半Markov 更新理論結合Laplace 及Laplace-Stieltjes 變換技術分析系統狀態轉移概率和系統再生狀態的平均逗留時間,推導系統穩態可用度、維修人員忙期穩態概率和系統穩態維修次數的可靠性指標以及系統單位時間內凈收益的經濟指標,給出確定不同條件下貯備模型的優化選擇算法.

為便于理解,模型中主要變量和符號如表1 和表2 所示.

表1 模型中主要變量說明Table 1 Main variables involved in models

表2 模型中主要符號說明Table 2 Main symbols involved in models

1 系統冷貯備模型分析

該模型下系統由三個同類型的設備組成,其中一個運行,另外兩個冷貯備(即貯備期間設備既不失效也不老化).令隨機變量X表示設備在運行期間的壽命,Z表示失效設備的維修時間.因為電子設備的壽命多數服從指數分布或近似服從指數分布[27],而失效設備的維修時間由多種因素決定,如維修人員的維修水平、失效設備的復雜程度以及維修工具的先進性等因素.因此維修時間往往不服從某一特定類型的分布[28].所以設運行設備壽命服從參數為λ的指數分布F(t,λ),失效設備維修時間服從一般分布G(t),即X～F(t,λ),Z～G(t).經分析,此系統共有6 個不同狀態:

為了建立系統在再生狀態下的更新方程,需要將這些狀態進行狀態劃分.根據X～F(t,λ),Z～G(t),通過分析易知,系統進入狀態S0,S1,S2,S3和S4的時刻均是系統的再生時刻(又稱再生點),而進入狀態S5的時刻是非再生時刻.因此S0,S1,S2,S3和S4是再生狀態,S5是非再生狀態(又稱滑過狀態)且是失效狀態.狀態之間的轉移關系如圖1所示.

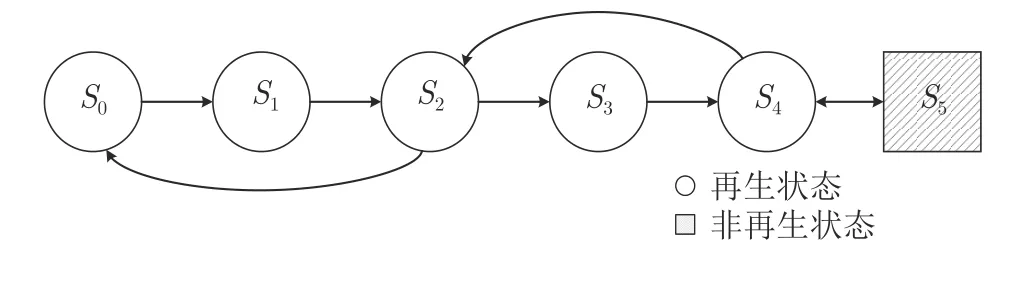
圖1 冷貯備系統狀態轉移圖Fig.1 State transition diagram of the cold-standby system

1.1 系統半Markov 核函數

令X(t)=Sj表示時刻t系統處于狀態Sj,Tn表示系統第n次狀態轉移時刻,Zn=X(Tn+0)表示第n次轉移時刻系統進入的狀態,容易驗證{Zn,Tn,n ∈N} 是狀態空間E={Sj|j=0,···, 5} 上的Markov 更新過程,{X(t),t≥0} 是半Markov過程.因此需對系統的半Markov 核函數Qij(t),i,j=0,···, 5進行分析.如圖1 所示.

1)當系統處于S0時,如果運行設備失效,則其中一個冷貯備設備被立刻激活,此時系統轉移至S1.因此,Q01(t)可表示為

2)當系統處于S1時,如果冷貯備設備激活完成,則該設備進入運行狀態,且失效設備進入維修狀態.此時系統轉移至S2.因此,Q12(t)可表示為

3)當系統處于S2時,此時有下述兩種情況:

a)如果維修設備在運行設備失效前修好,則系統轉移至S0.因此,Q20(t)可表示為

b)反之,如果運行設備在維修設備修好前失效,則該設備進入等待維修狀態且維修設備立刻暫停維修,冷貯備設備被激活.此時系統轉移至S3.因此,Q23(t)可表示為

4)當系統處于S3時,冷貯備設備激活完成時,該設備進入運行狀態,暫停維修的設備開始繼續維修,此時系統轉移至 S4.因此,Q34(t)可表示為

5)當系統處于S4時,此時有下述兩種情況:

a)如果維修設備在運行設備失效前修好,則修好后的設備進入冷貯備狀態,等待維修的設備開始維修,此時系統進入S2.因此,Q42(t)可表示為

b)反之,如果運行設備在維修設備修好前失效,則系統轉移至S5.因此,Q45(t)可表示為

1.2 系統所有再生狀態的平均逗留時間

令μi和Fi(t),i=0,1,2,3,4,分別表示系統在狀態Si的平均逗留時間和概率分布函數.令Pi(t)表示系統在狀態Si的存活函數,即Pi(t)=1-Fi(t)=(t).對每個狀態的平均逗留時間μi進行分析可得

1.3 系統性能指標

對系統穩態可用度、維修人員穩態忙期概率以及系統穩態平均維修次數三個性能指標進行分析.

1.3.1 系統穩態可用度

設當前時刻系統處于狀態S0,經過時間t后,根據系統狀態是否發生變化,存在兩種情況: 1)如果沒有發生變化,即系統依然停留在S0,此種情況可表示為P {X ≥t}.此時系統的瞬時可用度為A0(t)=P {X ≥t}·1=P {X ≥t}.2)如果系統狀態發生變化,如圖1 所示系統只能轉移到S1.此時根據Markov 更新理論,系統瞬時可用度為

其中,符號 “?” 表示卷積運算符.根據概率加法原理可得:A0(t)=Q01(t)?A1(t)+P{X ≥t}.同理可得系統在其余再生狀態S1,S2,S3,S4下的瞬時可用度更新方程.從而系統瞬時可用度的更新方程組為

對式(13)進行Laplace 變換得

解式(14)可得

根據Abel 定理,系統穩態可用度為

1.3.2 維修人員穩態忙期概率

與第1.3.1 節類似,首先建立維修人員在t時刻忙期的瞬時概率更新方程組

對式(17)進行Laplace 變換得

解式(18)可得

根據Abel 定理,維修人員穩態忙期概率為

1.3.3 系統穩態平均維修次數

同理,建立系統在 (0,t] 時間內維修次數的更新方程組

對式(21)進行Laplace-Stieltjes 變換得

解式(22)可得

其中,Γ4(s)和 Γ6(s)與式(19)中相同.

根據Abel 定理,可得系統穩態平均維修次數為

其中,NV=p23+p42.

1.3.4 系統穩態激活概率

建立系統在t時刻的激活概率更新方程組

對式(25)進行Laplace 變換得

解式(26)可得

Γ6(s)與式(19)中相同.

根據Abel 定理,系統穩態激活概率為

1.4 系統單位時間內產生的經濟效益

系統單位時間內的經濟效益 Θ1等于系統的運行收益減去設備的維修費用、支付給維修人員的費用、系統激活期間的停工費用以及系統的安裝費用.因此

其中,c0,c1,c2,c3分別表示系統單位時間內的運行收益、設備維修費用、支付給維修人員的費用、停工費用,I表示一個設備的安裝費用.

2 系統溫貯備模型分析

該模型下系統由三個同類型的設備組成,其中一個設備運行,另外兩個設備溫貯備(即貯備設備在溫和的環境下運行,其失效率低于運行設備).令隨機變量Xi,i=1,2,3 表示第i個設備在運行期間的壽命,Yi表示第i個設備在貯備期間的壽命,Zi表示第i個設備失效后的維修時間,F(t,λ)表示參數為λ的指數分布,G(t)和G1(t)表示一般分布.假設運行設備和溫貯備設備的壽命分別服從參數為λ和λ1的指數分布,即Xi～F(t,λ),Yi～F(t,λ1).運行設備和溫貯備設備失效后的維修時間均服從一般分布,但實際系統中這兩種維修時間往往不同,需要分別考慮.因此,如果Zi是運行設備失效后的維修時間,則Zi～G(t);反之,如果Zi是溫貯備設備失效后的維修時間,則Zi～G1(t).為了便于描述模型,進一步假設:

1)X1,X2,X3,Y1,Y2相互獨立.

2)系統不同狀態之間的轉移是瞬時的.

3)設備失效后,如果沒有其他設備正在維修,則維修人員立刻對該設備進行維修;否則,該設備進入等待狀態直到其他設備維修完成.設備修復后,其壽命分布像新的設備一樣.

經分析可得系統共有13 個狀態:

與冷貯備模型分析過程相同,經分析可得:S0,S1,S2,S7和S12是再生狀態;S3,S4,S5,S6,S8,S9,S10和S11是非再生狀態;S5,S6,S8和S11是失效狀態.狀態之間的轉移關系如圖2 所示.

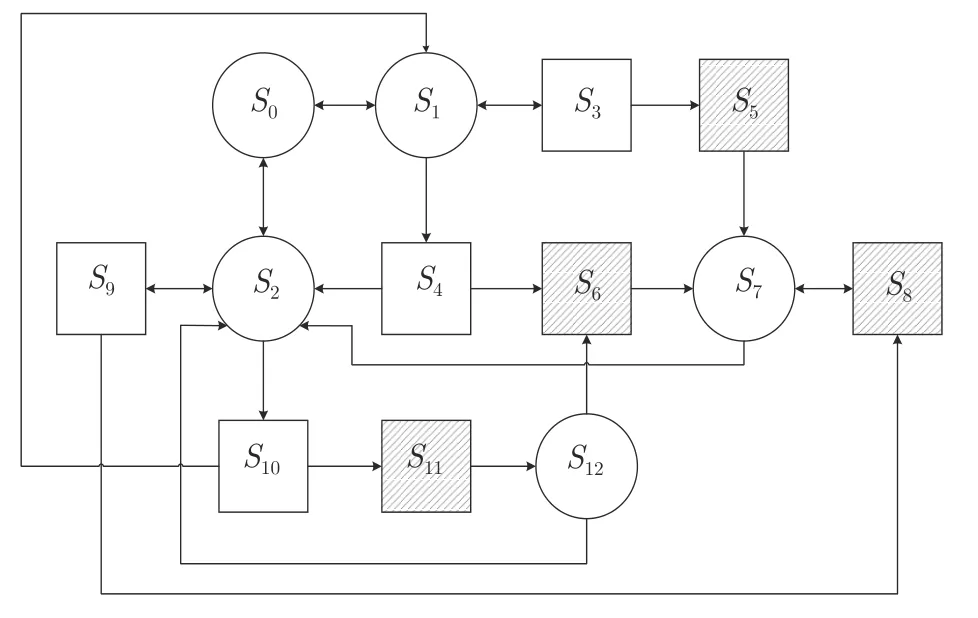
圖2 溫貯備系統狀態轉移圖Fig.2 State transition diagram of the warm-standby system

2.1 系統半Markov 核函數

與第1.1 節類似,經分析可得溫貯備模型下系統所有半Markov 核函數為(具體分析過程見附錄A)

2.2 系統在所有再生狀態的平均逗留時間

與第1.2 節類似,經分析可得系統在每個再生狀態的平均逗留時間μi,i=0,1,2,7,12 為(具體分析過程見附錄B)

2.3 系統性能指標

本節對系統的穩態可用度、維修人員穩態忙期概率和系統穩態平均維修次數三個性能指標進行分析.

2.3.1 系統穩態可用度

與第1.3.1 節類似,經分析可得系統穩態可用度為

2.3.2 維修人員穩態忙期概率

與第1.3.2 節類似,經分析可得維修人員穩態忙期概率為

2.3.3 系統穩態平均維修次數

與第1.3.3 節類似,經分析可得系統穩態平均維修次數為

2.4 系統單位時間內產生的經濟收益

與第1.4 節類似,溫貯備系統單位時間內產生的經濟效益 Θ2可表示為

其中,參數c4,c5,c6的含義分別與式(29)中的c0,c1,c2相同.

3 系統熱貯備模型分析

雙貯備設備下熱貯備系統實質上是三個設備以并聯的方式工作.該模型中不考慮某個設備失效后負載均衡對其他運行設備失效率造成的影響.因此三個設備的失效率和維修率均視為相同.實際上,該模型的分析方法與溫貯備系統模型的分析方法相同,在分析過程中只需令λ1=λ,β1=β即可.因此,該模型的分析過程略.下面只給出系統單位時間內的凈收益函數

其中,參數c7,c8,c9的含義分別與式(29)中的c0,c1,c2相同.

4 系統冷/溫/熱貯備模型優化選擇算法

從系統性能指標(即穩態可用度、維修人員穩態忙期概率、系統穩態平均維修次數)以及經濟指標(即系統單位時間內凈收益)兩個方面,分別給出雙貯備系統冷/溫/熱貯備模型的優化選擇算法.

算法 1.以系統性能為目標的雙貯備系統冷/溫/熱貯備模型優化選擇算法

算法 2.以系統單位時間內凈收益為目標的雙貯備系統冷/溫/熱貯備模型優化選擇算法

5 實例分析

以實際的雙貯備PLC (Programmable logic controller)控制系統(如圖3 所示)為研究對象,進行實例分析.從系統性能指標,即系統穩態可用度、維修人員穩態忙期概率、系統穩態平均維修次數,以及經濟指標,即系統單位時間內凈收益兩個方面,對系統貯備模型優化算法的輸入參數進行假設.

圖3 雙貯備冗余控制系統Fig.3 Redundancy control system with dual-standby device

為了給出合理的參數假設,首先對圖3 所示的系統進行簡要描述.該PLC 控制系統是我國某自動化廠商自主研制的高可靠雙貯備控制系統.系統中每個PLC 設備經過加速壽命測試后得到平均工作壽命約為1800 天,因此運行設備的平均失效率設為λ=0.00055 (個/天).溫貯備設備失效率與工作環境有關,設其為λ1∈[0.00001,0.00055] (個/天).維修時間一般服從指數分布,即G(t)=1-e-βt,.其中參數β,β1分別表示運行設備和溫貯備設備失效后的平均維修率.實際上,設備失效后需要返廠、檢測、維修、測試、現場安裝調試、重新運行等環節.因此根據設備歷史維修數據可得運行設備失效后從返廠到重新運行約為7～30 天,溫貯備設備約為5 到15 天.因此設β ∈[0.03,0.14](個/天),β1=[0.067,0.2] (個/天).該系統如果配成冷貯備模式,則當運行設備失效后,冷貯備設備能夠自動上電并上載控制程序以及導入設備失效前的數據,整個激活過程需要3 min 左右.通過對歷史激活數據的統計分析可得貯備設備激活時間服從正態分布,即

其中,參數γ和σ分別代表均值和方差.因此設γ=0.0021 (天),σ=0.0007.

5.1 以系統性能為目標的實例分析

5.1.1 以穩態可用度為目標的實例分析

令λ=0.00055,λ1=0.00011,β=0.05,β1=0.1,γ=0.0021,σ=0.0007,系統性能指標為穩態可用度.將這些參數代入算法1,在MATLAB (2014b)環境下運行算法1 (公式推導部分利用MATLAB的符號計算),其計算結果如表3 所示.

表3 系統穩態可用度Table 3 System steady-state availability

表3 中,模型I、模型II 和模型III 分別表示冷貯備模型、溫貯備模型和熱貯備模型.由表3 可知,.因此以系統穩態可用度為目標時,算法1 輸出為: 冷貯備是最優貯備模型.由于溫貯備設備的失效率與其工作環境有關,因此屬于可變參數,為了研究該參數對系統穩態可用度的影響,令λ1從 0.00001 變化到 0.00055,步長為 0.00001,其他參數不變.將這些參數重新代入算法1,其計算結果如圖4 所示.

圖4 λ1 對三個模型的穩態可用度的影響Fig.4 Impact of λ1 on steady-state available of the three models

由圖4 可知,溫貯備系統的穩態可用度隨λ1的增加而降低.?λ1∈[0.00001,0.00055],溫貯備系統的穩態可用度均小于冷貯備系統,但均大于熱貯備系統.可見溫貯備設備的失效率對溫貯備系統穩態可用度有一定影響,但對算法1 輸出結果即最優貯備模型沒有影響.

5.1.2 以維修人員忙期穩態概率為目標的實例分析

參數λ,λ1,β,β1,γ,σ取值與第5.1.1 節相同,系統性能指標為維修人員忙期穩態概率.將這些參數代入算法1,其計算結果如表4 所示.

表4 維修人員忙期穩態概率Table 4 Steady-state probability of repairmen busy

由表4 可知,.因此以維修人員穩態忙期概率為目標時,算法1 輸出結果為: 冷貯備是最優貯備模型.實際上,運行設備和溫貯備設備失效后的維修率(即參數β,β1)對維修人員穩態忙期概率有直接影響,因此,令β∈[0.03,0.14],β1=[0.067,0.2],兩個參數的變化步長均設為0.005,其他參數不變,研究β對,的影響以及β,β1對的影響.其結果分別如圖5 和圖6 所示.

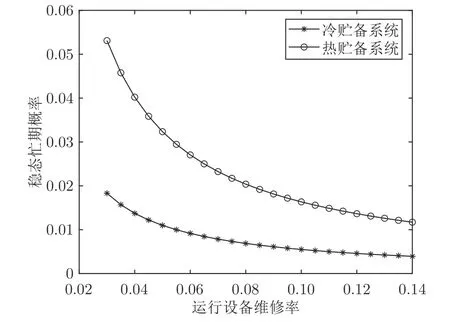
圖5 運行設備維修率對冷、熱貯備系統中維修人員穩態忙期概率的影響Fig.5 Impact of repair rates for the working device on steady-state probability of repairmen busy for cold,hot-standby system

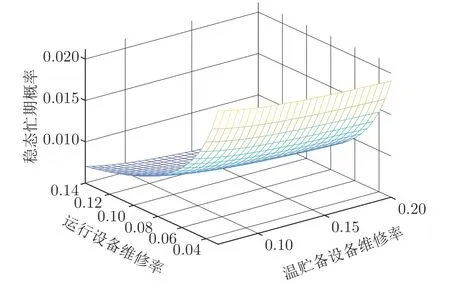
圖6 運行設備和溫貯備設備的維修率對溫貯備系統中維修人員穩態忙期概率的影響Fig.6 Impact of repair rates for the working and warm-standby devices on steady-state probability of repairmen busy for warm-standby system

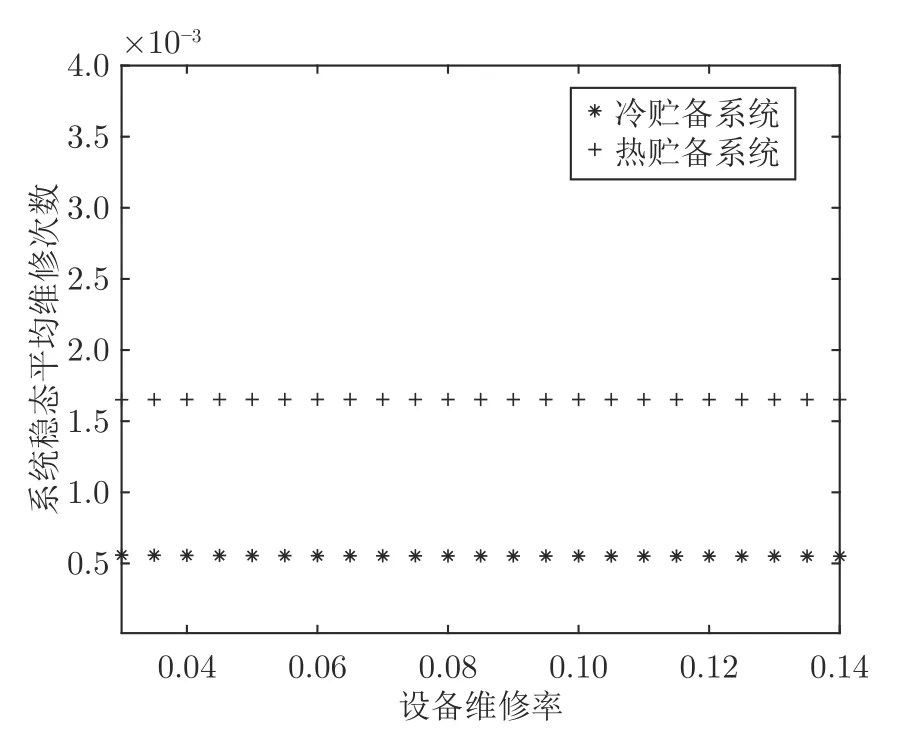
圖7 設備維修率對冷、熱貯備系統穩態平均維修次數的影響Fig.7 Impact of repair rate on mean repair number of the cold,hot-standby systems in steady-state

圖8 運行設備的維修率和溫貯備設備的失效率對系統穩態平均維修次數的影響Fig.8 Impact of repair rate of the working device and failure rate of the warm-standby device on repair number of the system in steady-state

由圖5 可知,在參數β的取值范圍內變化時,均小于.說明以維修人員穩態忙期概率為目標時,算法1 輸出是: 冷貯備是最優貯備模型.由圖6 可知,隨β,β1的增大呈非線性減小.從數值計算結果可知: 當β取值相同時,總成立.說明在相同的運行設備維修率下,算法1輸出依然是: 冷貯備是最優貯備模型.

5.1.3 以系統穩態平均維修次數為目標的實例分析

參數λ,λ1,β,β1,γ,σ取值與第5.1.1 節相同,系統性能指標為系統穩態平均維修次數.將這些參數代入算法1.其計算結果如表5 所示.

表5 系統穩態平均維修次數Table 5 Mean repair number of the system in steady-state

5.2 以系統經濟效益為目標的實例分析

根據系統應用案例中的歷史財務數據和歷史維修費用記錄,給出三個模型下凈收益中費用的合理范圍: 設c0,c4,c7∈ [1000,5000] (元/h),c1,c5,c8∈[300,500] (元/h),c2,c6,c9∈[300,700] (元/h).實際上,冷貯備系統激活期間的停機對于不同行業的生產制造企業帶來的經濟損失或產生的費用大相徑庭、難以估計.但根據使用該系統的某生產企業的停機記錄,停機費用的合理范圍為:c3∈[500,1000](元/h),系統安裝費用的合理范圍為:I ∈[100,300](元/h).

5.2.1 以系統單位時間內運行收益為研究對象

令參數λ,λ1,β,β1,γ,σ取值與第5.1.1 節相同,令參數c1=400,c2=500,c3=800,c5=100,c6=200,c8=300,c9=500,I=200,c0,c4,c7∈[1000,5000].將以上參數代入算法2,其計算結果如下.

對于情況a),化簡后最終不等式為

該不等式在?c0,c4,c7∈[1000,5000] 取值范圍內有解,即 Θ1≥max(Θ2,Θ3)成立,此時算法2輸出結果是: 冷貯備是最優貯備模型.

對于情況b),化簡后的最終不等式為

該不等式在?c0,c4,c7∈[1000,5000] 取值范圍內有解,即 Θ2≥max(Θ1,Θ3)成立,此時算法2輸出結果是: 溫貯備是最優貯備模型.

對于情況c),化簡后最終不等式為

該不等式在?c0,c4,c7∈[1000,5000] 取值范圍內有解,即 Θ3≥max(Θ1,Θ2)成立,此時算法2輸出結果是: 熱貯備是最優貯備模型.

5.2.2 以系統單位時間內設備維修費用為研究對象

令c0=3000,c4=3000,c7=3000,c1,c5,c8∈[300,500],其他參數與第5.2.1 節相同.將以上參數代入算法2,其計算結果如下.

對于情況a),化簡后的最終不等式為

該不等式在?c1,c5,c8∈[300,500] 取值范圍內恒成立,即 Θ1≥max(Θ2,Θ3)恒成立,此時算法2輸出結果是: 冷貯備是最優貯備模型.

對于情況b)和情況c),化簡后分別得最終不等式為

然而,在?c1,c5,c8∈[300,500] 取值范圍內,以上兩個不等式均無解.即,Θ2≥max(Θ1,Θ3)和Θ3≥max(Θ1,Θ2)均不成立,此時算法2 無輸出.說明以系統單位時間內設備維修費用為研究對象時,無論參數如何取值,冷貯備均是最優貯備模型.

5.2.3 以單位時間內支付給維修人員的費用為研究對象

令c0=3000,c4=3000,c7=3000,c2,c6,c9∈[300,700],其他參數取值與第5.2.1 節相同.將以上參數代入算法2,其計算結果如下.

對于情況a),化簡后的最終不等式為

該不等式在?c2,c6,c9∈[300,700] 取值范圍內恒成立,即 Θ1≥max(Θ2,Θ3)恒成立.此時算法2輸出結果是: 冷貯備是最優貯備模型.

對于情況b)和情況c),化簡后分別得到的最終不等式為

然而,在?c2,c6,c9∈[300,700] 取值范圍內,以上兩個不等式均無解,即 Θ2≥max(Θ1,Θ3)和Θ3≥max(Θ1,Θ2)均不成立.此時算法2 無輸出.說明以系統單位時間內支付給維修人員費用為研究對象時,無論參數如何取值,冷貯備均是最優貯備模型.

6 結束語

針對選擇哪種貯備模型才能使雙貯備系統實現性能和經濟效益最優的問題,本文創新性地提出了雙貯備系統貯備模型優化選擇算法.通過分析系統狀態及半Markov 核函數分別建立了系統冷/溫/熱貯備模型下的更新方程組,利用Laplace、Laplace-Stieltjes 變換技術和Abel 定理求得了系統穩態可用度、維修人員穩態忙期概率和系統穩態平均維修次數的系統性能指標,并給出了系統單位時間內凈收益的目標函數,之后通過模型對比分析給出了分別以系統性能指標和經濟指標為目標的系統貯備模型優化選擇算法.最后以實際的國產雙貯備控制系統作為研究對象,對所提算法進行實例分析,實例結果表明所提算法能夠有效地確定系統在不同條件下的最優貯備模型.本文是在系統確定參數或確定參數變化范圍的情況下進行研究的.然而對于某些實際的工業現場,現場環境復雜,系統部分參數無法測量,這些參數屬于不確定參數.對具有不確定參數的雙貯備系統如何進行分析、建模并給出貯備模型的優化選擇算法是下一步重點研究的問題.

附錄A

對溫貯備模型下系統所有半Markov 核函數進行分析如下.

1)當系統處于S0時,如果其中一個溫貯備設備先于運行設備失效,則系統轉移至S1.此時有

反之,如果運行設備先于溫貯備設備失效,則系統轉移至S2.此時有

2)當系統處于S1時,此時有下述幾種情況:

a)如果失效設備在運行設備和溫貯備設備失效前已修好,則系統轉移至S0.此時有

b)如果溫貯備設備在失效設備修好前失效且在該失效時刻運行設備依然運行,則系統轉移至S3,然而由于S3是非再生狀態,因此當系統進入S3后會再次轉移至哪些狀態需要分別考慮.

c)如果維修設備在運行設備失效前已修好,則系統由S3轉移至S1,此時有

d)如果運行設備在失效設備修好前失效,則系統將由S3再次轉移至S5,此時有

e)當系統轉移至S5后,正在維修的設備修好后,系統將轉移至S7.此時有

當系統處于S1時,如果運行設備在維修設備修好前失效且在失效時刻溫貯備設備沒有失效,則系統轉移至S4.由于S4是非再生狀態,因此系統由S4轉移至哪些狀態需要分別考慮.

f)如果失效設備在運行設備失效前已修好,則系統將由S4轉移至S2.此時有

g)反之,如果運行設備在失效設備修好前失效,則系統將由S4轉移至S6.此時有

h)當系統轉移至S6后,正在維修的設備修好后,系統將轉移至S7.此時有

3)當系統處于S2時,此時有下述幾種情況:

a)如果維修設備在運行設備和溫貯備設備失效前已修好,則系統轉移至S0.此時有

b)如果溫貯備設備在維修設備修好前失效,且在失效時刻運行設備正常運行,則系統轉移至S10,由于S10是非再生狀態,因此系統由S10轉移至哪些狀態需要分別考慮.

c)如果維修設備在運行設備失效前已修好,則系統由S10轉移至S1.此時有

d)反之,如果運行設備在維修設備修好前失效,則系統由S10轉移至S11.此時有

e)當系統轉移至S11后,維修設備修好后,系統轉移至S12.此時有

當系統處于S2時,如果運行設備在維修設備修好前失效且在失效時刻溫貯備設備沒有失效,則系統轉移至S9.由于S9是非再生狀態,因此由S9轉移至哪些狀態需要分別考慮.

f)如果維修設備在運行設備失效前已修好,則系統由S9轉移至S2.此時有

g)如果運行設備在維修設備修好前失效,則系統由S9轉移至S8.系統處于S8后,維修設備修好后,系統由S8轉移至S7.此時有

4)當系統處于S7時,此時有下述幾種情況:

a)如果正在維修的設備在運行設備失效前已修好,則系統轉移至S2.此時有

b)反之,如果運行設備在維修設備修好前失效,則系統轉移至S6.系統處于S6后,當維修設備修好后,系統由S6轉移至S7.此時有

5)當系統處于S12時,此時有下述幾種情況:a)如果維修設備在運行設備失效前已修好,則系統轉移至S2,此時有

b)反之,如果運行設備在維修設備修好前失效,則系統轉移至S6.系統處于S6后,當維修設備修好后,系統由S6轉移至S7.此時有

附錄B

對溫貯備模型在所有再生狀態的平均逗留時間進行分析如下.

1)從系統進入S0開始(t=0),經過時間t后,如果運行設備和溫貯備設備均未失效,則有

2)從系統進入S1開始(t=0),經過時間t后,如果運行設備和溫貯備設備沒有失效,且正在維修的設備沒有修好,則有

3)從系統進入S2開始(t=0),經過時間t后,如果運行設備和溫貯備設備沒有失效,且正在維修的設備沒有修好,則有

4)從系統進入S7開始(t=0),經過時間t后,如果運行設備沒有失效且正在維修的設備沒有修好,則有

5)從系統進入S12開始(t=0),經過時間t后,如果運行設備沒有失效且正在維修的設備沒有修好,則有