巧用平移建聯(lián)系，數(shù)形結(jié)合探性質(zhì)

張艷

摘? ?要：從單元整體視角出發(fā)，通過喚醒學生學習y=ax2的相關(guān)內(nèi)容與經(jīng)驗，結(jié)合解析式、表格、圖象，引導(dǎo)學生探究y=a（x-h）2與y=ax2從數(shù)到形的區(qū)別與聯(lián)系，從而自主得到形如y=a（x-h）2的二次函數(shù)圖象與性質(zhì).數(shù)形結(jié)合是解決函數(shù)問題的重要數(shù)學思想 .從特殊到一般，利用平移探究函數(shù)圖象是初中階段研究函數(shù)的重要方法.

關(guān)鍵詞：單元整體；深度學習；直觀想象；代數(shù)推理；類比遷移

華羅庚曾說過“數(shù)缺形時少直觀，形少數(shù)時難入微”，二次函數(shù)因其既有解析式又有圖象，利用數(shù)形結(jié)合思想常常能夠巧妙地解決相關(guān)問題.在新授課的教學中，就應(yīng)該注重數(shù)形結(jié)合的滲透.然而由于二次函數(shù)解析式形式相比于一次函數(shù)更多樣，圖象性質(zhì)也比一次函數(shù)更復(fù)雜，學生在解析式系數(shù)與圖象的關(guān)系上更容易混淆.因此在二次函數(shù)圖象和性質(zhì)一節(jié)中，針對從y=ax2到y(tǒng)=a（x-h）2+k的探究，若能從單元整體視角設(shè)計，結(jié)合函數(shù)的平移，即可以讓學生更深刻地理解不同形式的二次函數(shù)解析式之間的關(guān)系，又可以讓數(shù)形結(jié)合的滲透更加水到渠成.下面將以y=a（x-h）2圖象與性質(zhì)一節(jié)課教學設(shè)計為例，闡釋如何借助單元整體視角，抓住解析式從特殊到一般的內(nèi)在關(guān)聯(lián)，自然地滲透數(shù)形結(jié)合思想.

1? 回顧舊知，喚醒研究方法

（1）在坐標紙上畫出函數(shù)y=x2的圖象，并歸納步驟.

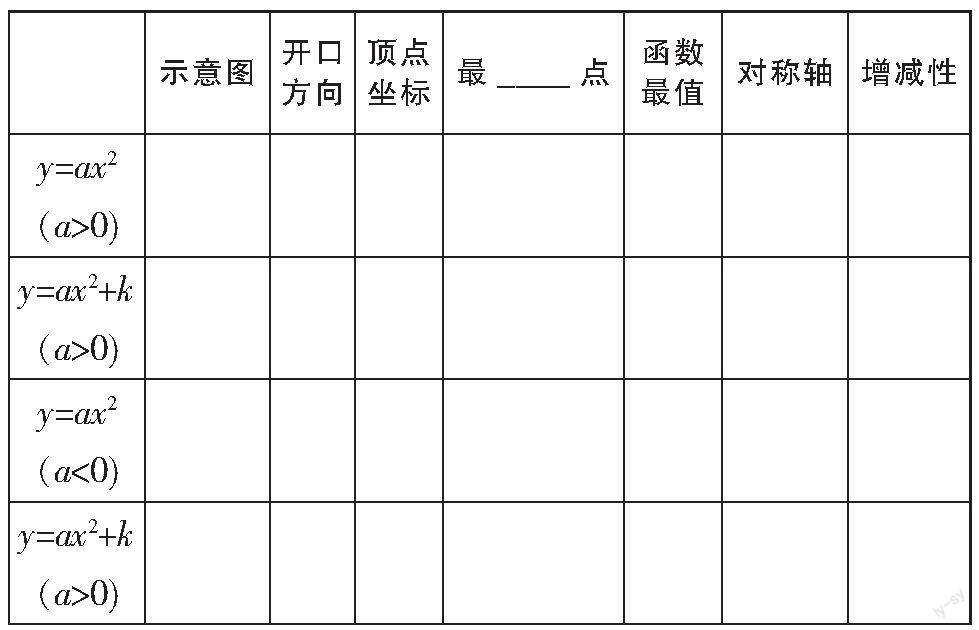
（2）以表格形式讓學生回顧，如表1.

（3）問題1：從解析式和圖象上思考y=ax2與y=ax2+k的聯(lián)系.

問題2：k的意義？

設(shè)計意圖：（1）畫y=x2函數(shù)圖象既能讓學生回顧研究函數(shù)圖象與性質(zhì)的一般步驟，其表格和圖象對后續(xù)新函數(shù)y=（x-1）2還起到參照作用，更直觀地得出兩個函數(shù)之間的聯(lián)系.（2）表格的呈現(xiàn)，一方面讓學生回憶起前兩次課從哪些方面研究二次函數(shù)圖象與性質(zhì)，另一方面直觀地感受y=ax2與y=ax2+k在填寫內(nèi)容上的區(qū)別與聯(lián)系，從而使學生更好地回憶起后續(xù)的兩個問題.（3）問題1提示學生從數(shù)和形兩方面思考聯(lián)系，代數(shù)方面，解析式y(tǒng)=ax2+k比y=ax2多了一個k，圖象方面，y=ax2+k可以由y=ax2上（下）平移k個單位得到.這兩方面聯(lián)系均與k有關(guān)，從而引出k的意義：從數(shù)上說，他是自變量為0時的函數(shù)值，從形上看，他是函數(shù)與y軸交點的縱坐標.

2? 研究方法遷移，探索表格奧秘

任務(wù)：以y=（x-1）2為例，研究形如y=a（x-h）2的函數(shù)圖象與性質(zhì).

步驟1：列表

問題1：許多同學填寫表2的第一行延續(xù)了表3第一行的取值，回憶表3的畫圖過程，這種自變量取值方式對畫圖有何幫助？可以得出什么結(jié)論？

問題2：猜想y=（x-1）2圖象是否也會關(guān)于y軸對稱？是否也具有對稱性？

問題3：未畫圖，如何讓猜想更具有說服力？

問題4：表2的自變量取值有沒有更好的方式？

問題5：填好表2后，通過表格，你能初步想象出y=（x-1）2的圖象形狀與位置嗎？

設(shè)計意圖：函數(shù)表格中的每一列x，y和點坐標一一對應(yīng)，因此表格中數(shù)的規(guī)律可以反映其圖形特征.通過問題1，喚醒學生通過兩對y值相等得出對稱軸從而畫出對稱的函數(shù)圖象這一經(jīng)驗，思考表2的填寫方式，調(diào)整自變量的取值，使得y的值與表3相同.從而透過表格驗證問題2的猜想.在動手畫圖之前提出問題5，旨在發(fā)展學生的直觀想象能力，滲透數(shù)形結(jié)合思想.

3? 畫圖驗證猜想，直觀揭示聯(lián)系

步驟2：在坐標紙上描點，連線，獲得函數(shù)圖象.

問題1：通過5個點，我們描繪出的函數(shù)圖象直觀上看是關(guān)于x=1對稱的，你能利用點與圖象的位置關(guān)系證明這個結(jié)論嗎？

問題2：將函數(shù)y=（x-1）2補充在表1最后一行下方，自行完成相關(guān)性質(zhì)的填寫.

問題3：結(jié)合上課初始所畫y=x2的圖象，思考二者聯(lián)系.

問題4：你是如何發(fā)現(xiàn)二者聯(lián)系的？

問題5：利用表格，能否佐證你的發(fā)現(xiàn)？

問題6：結(jié)合表格，思考如何證明y=（x-1）2可由y=x2向右平移1個單位得到？

設(shè)計意圖：直觀的結(jié)論需要通過嚴謹?shù)耐评矸娇沙闪ⅲ瑔栴}1和6對學生的要求較高，例如問題1學生需要設(shè)x=a，帶入解析式得到y(tǒng)的值，再將A（a，（a-1）2）通過x=1對稱得到新的點坐標A' （2-a，（a-1）2），最后驗證A'落在y=（x-1）2上.設(shè)計問題1，可以發(fā)展學生的代數(shù)推理能力，也讓學生進一步體會形的直觀與數(shù)的嚴謹.

利用課前的知識回顧表格，能更直觀地感受y=（x-1）2和之前的函數(shù)在性質(zhì)上的區(qū)別與聯(lián)系.問題3-5引導(dǎo)學生思考產(chǎn)生這些聯(lián)系的本質(zhì)原因.問題3 先從圖象入手，能較為直觀地得到平移的關(guān)系，再從兩個表格第一行每個數(shù)值對應(yīng)差1，第二行相同，這一代數(shù)角度印證5個點存在平移關(guān)系，問題6要求學生將5個點的平移關(guān)系一般化到任意點，從而推理證明結(jié)論，再次讓學生經(jīng)歷由直觀猜想到嚴謹論證的思維過程，培養(yǎng)學生思維的嚴謹性.

4? 從特殊到一般，歸納圖象性質(zhì)

步驟3：以y=（x-1）2的圖象性質(zhì)結(jié)論，推廣得出y=a（x-h）2的函數(shù)圖象與性質(zhì)

問題1：不畫圖，你能說出y=（x-2）2是如何由y=x2平移得到的嗎？

問題2：解析式如何反映平移情況？

問題3：將函數(shù)y=（x-h）2補充在表1最后一行下方，自行完成相關(guān)性質(zhì)的填寫

問題4：y=（x-h）2與y=x2解析式是否也有相同之處？

問題5：將函數(shù)y=a（x-h）2繼續(xù)補充在表1最后一行下方，完成相關(guān)性質(zhì)的填寫

問題6：類比y=ax2+k中k的意義，思考h的意義

設(shè)計意圖：通過問題1，2讓學生感受解析式中參數(shù)h和圖象平移之間的關(guān)系，利用控制變量法，先讓學生理解y=（x-h）2與y=x2的平移關(guān)系后，通過問題4，讓學生關(guān)注到二者的二次項系數(shù)相同，再次體會參數(shù)a決定了二次函數(shù)圖象的開口大小與方向，即二次函數(shù)的形狀.從而自然地將y=a（x-h）2與y=ax2聯(lián)系起來，得到y(tǒng)=a（x-h）2的圖象與性質(zhì).

5? 教學思考

《義務(wù)教育數(shù)學課程標準（2022年版）》中指出，課程目標的確定，立足學生核心素養(yǎng)發(fā)展，集中體現(xiàn)數(shù)學課程育人價值.而結(jié)構(gòu)化、情境化、凸顯學科大概念的知識，發(fā)展核心素養(yǎng)的功能最強.單元是知識結(jié)構(gòu)化的重要表現(xiàn)，深度學習倡導(dǎo)單元學習[ 1 ].二次函數(shù)解析式形式多樣，人教版《義務(wù)教育教科書數(shù)學》九年級上冊“二次函數(shù)的圖象和性質(zhì)”中包含了y=ax2，y=ax2+k，y=a（x-h）2和y=a（x-h）2+k四部分內(nèi)容，傳統(tǒng)教學中教師往往是通過對某個具體函數(shù)進行五點法畫圖，觀察圖象特征，或通過幾何畫板展示若干同樣形式的函數(shù)圖象，由學生觀察共性，從而得到函數(shù)性質(zhì).采用這樣的教學設(shè)計，學生往往是以孤立的方式記憶每個形式解析式的圖象性質(zhì)，對于學困生而言，知識容易遺忘混淆.本節(jié)課從單元整體視角出發(fā)，抓住研究函數(shù)圖象的基本步驟：列表，描點，連線，將y=（x-1）2和y=x2分別從表格、點、圖象方面進行對比，從數(shù)和形感知二者的平移關(guān)系，使學生在掌握了y=ax2圖象性質(zhì)的基礎(chǔ)上，僅需部分調(diào)整，就能得到y(tǒng)=a（x-h）2的圖象性質(zhì).這種教學設(shè)計同樣適用于研究y=ax2+k，即教材中探究完y=ax2后，對于y=a（x-h）2和y=ax2+k的探究是不分先后的.只不過由于y=ax2+k和y=ax2的關(guān)系與正比例和一次函數(shù)的關(guān)系類似，從認知理論來說，先研究y=ax2+k學生更好接受.在該設(shè)計下，對于y=a（x-h）2+k，學生完全有能力自己獨立探究，獲得圖象性質(zhì)，從而建立起二次函數(shù)圖象與性質(zhì)的知識網(wǎng)絡(luò).

另外，新課標強調(diào)邏輯推理不僅僅存在于幾何中，代數(shù)也應(yīng)該關(guān)注推理能力的滲透.因此在觀察出圖象對稱，以及圖象間的平移關(guān)系后，嘗試著要求學生通過代數(shù)推理論證.該要求一方面能夠讓學生完整地經(jīng)歷觀察—猜想—論證的思維過程，強化學生思維的嚴謹性；另一方面示范了如何借助點坐標完成坐標系背景下相關(guān)圖形猜想的證明，由數(shù)證形，滲透了數(shù)形結(jié)合思想，為解析幾何打下基礎(chǔ).

參考文獻：

［1］ 劉月霞，郭華.深度學習：走向核心素養(yǎng)（理論普及讀本）[M].北京：教育科學出版社，2018.