濾波器階數對導航接收機時域抗干擾的影響分析*
孫廣富,宋 捷,魯祖坤,李柏渝,肖志斌,郭海玉
(國防科技大學 電子科學學院, 湖南 長沙 410073)
時域抗干擾是衛星導航接收機的常用抗干擾技術,其利用信號與干擾在頻譜上存在的差異特點,設計自適應濾波器在時域濾除干擾信號,是窄帶干擾的主要抑制技術之一[1]。由于在實際應用中常常面臨速度、規模、功耗等硬件問題,高抗干擾需求對抗干擾濾波器性能提出了更高要求[2]。因此,基于時域自適應抗干擾濾波器的復雜度研究是導航接收機應用的重要課題。在導航接收機時域抗干擾中應用的自適應算法,如最小均方(least mean square,LMS)算法、遞歸最小二乘(recursive least squares, RLS)算法、Levinson-Durbin算法以及Burg算法等,都在抗窄帶干擾中取得了良好的效果[3-4]。該四種算法都采用最小均方誤差 (minimum mean square error, MMSE) 準則來設計濾波器,LMS算法和RLS算法更為常見[5-8]。其中,LMS算法由于其算法簡單、計算量小、易收斂等優點,常應用于實際工程應用中[9]。
自適應濾波器長度對LMS算法的影響涉及計算復雜度、收斂速度和穩態誤差,但是目前關于自適應算法基于濾波器長度對濾波性能影響的研究僅局限于定性分析[10]。早期研究中濾波器長度僅作為影響收斂速度等指標的一個因素參與談論,過短自適應濾波器的性能發散得到了證明,控制濾波器長度也被反復討論,并出現了幾種動態控制濾波器長度的算法[11-13]。但是,相關的階數研究基本從收斂時間和穩態誤差等算法性能出發,實用于導航接收機抗干擾性能研究的自適應濾波器階數分析和控制算法并不完善。
當前導航接收機中時域自適應抗干擾濾波器的階數選取嚴重依賴工程經驗而影響分析不足,通常在工程中將濾波器階數設置為一個較大值以滿足抗干擾需求,但會大大增加硬件復雜度。本文針對實用于導航接收機的濾波器階數分析不足的問題,開展了時域自適應濾波器階數對抗干擾性能的影響研究:首先建立導航接收機數字中頻信號抗干擾模塊的數學模型,在時域分別采用自適應LMS算法對干擾信號進行抑制;然后針對不同干擾環境分析濾波器階數對抗干擾性能的影響;通過軟件接收機和實物平臺對各類時域自適應抗干擾算法進行仿真和實測,驗證理論推導和分析的準確性;最后簡易提出一種基于抗干擾需求的最優階數設計方法。
1 數學模型
1.1 時域自適應抗干擾數學模型
如圖1所示,抗干擾型導航接收機的基帶數字信號處理器包含區別于其他類型導航接收機的抗干擾模塊。其接收來自數字下變頻的數字信號,用于完成窄帶干擾等常規干擾信號抑制[14]。

圖1 導航接收機信號處理器Fig.1 Navigation receiver signal processor
假設導航信號經數字下變頻后的信號、干擾和噪聲互不相關,分別為s(n)、j(n)和nnoise(n),抗干擾前信號為:
x(n)=s(n)+j(n)+nnoise(n)
(1)
無干擾條件下的載噪比為:
(2)
即為導航信號抗干擾后的理想載噪比。式中,Ss(f)和Sn(f)分別為導航中頻信號與噪聲的功率譜密度,Bn為噪聲帶寬。
導航接收機的時域抗干擾技術是通過自適應濾波器在時域上對信號進行濾波,來達到抑制干擾的目的[14]。假設M階濾波器的抽頭輸入量為:
xn=[x(n),x(n-1),…,x(n-M+1)]T
(3)
濾波權向量為:
WM=[w0,w1,…,wM]
(4)
則時域濾波器抗干擾后的輸出為:
(5)
自適應濾波器最常用最小均方算法,其利用梯度最陡下降使誤差信號均方值達到最小,具有計算量小、實現簡單的特性[15]。如圖2所示,抗干擾濾波器的輸出信號y(n)與期望信號d(n)之間存在誤差信號e(n):

圖2 時域自適應濾波器Fig.2 Time-domain adaptive filter
(6)
基于LMS自適應算法的抗干擾濾波器根據誤差信號調整WM,均方誤差的梯度向量為:
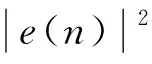
(7)
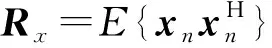
設置WM的初始值為WM,0,通過迭代使濾波權向量以步進μ沿負梯度方向變化:

(8)
式中,l為自適應迭代次數。
將式(7)代入式(8)得:
(9)
在實際應用中通常使用瞬時均方誤差代替均方誤差,最終得到LMS算法的遞推公式為:
(10)
自適應濾波器的頻率響應為:
H(f)=D(WM)
(11)
式中,D(·)表示離散時間傅里葉變換。
載噪比是抗干擾型衛星導航接收機的重要技術指標,抗干擾后載噪比估計值體現了抗干擾濾波器對干擾信號的抑制能力和對導航信號的完好保存能力,是對濾波器抗干擾性能的量化評估指標[16-17]。抗干擾后載噪比估計值為:
(12)
式中,Sy(f)是導航接收機抗干擾后信號的功率譜密度。
1.2 改進型LMS算法
LMS算法的穩態誤差與步長成正比,而收斂速度與步長成反比,變步長LMS算法是改進型LMS算法的一個重要研究分支,通過在初始收斂階段選取較大步長,在算法接近收斂時選取較小步長,可以解決這兩個性能指標之間的權衡,改善穩態誤差和不同階數濾波器下的收斂性[18]。改進型LMS算法的研究包括變步長LMS算法、變階數LMS算法、部分更新LMS算法和稀疏LMS算法等主要方向,并衍生出許多改進的方法,其中變步長LMS算法是最主要的算法改進方向[19-20]。
歸一化最小均方 (normalized least mean square,NLMS) 算法通過對抽頭向量進行歐式范數平方的歸一化,實現了步長隨時間變化:
(13)
歸一化變步長最小均方 (normalized variable step size least mean square,NVLMS)算法在LMS算法和NLMS算法的基礎上對時變步長進行了改進:
(14)
還有其他不同的改進型變步長LMS算法,例如文獻[21]提出的新變步長LMS算法中:
μ(l)=β(1-e-α|e(n)|2)
(15)
式中,μ0、α和β都是影響算法收斂性的可調參數。
2 基于復雜度的抗干擾性能分析
2.1 濾波器階數對抗干擾性能的影響
基于LMS算法的抗干擾濾波器代價函數為:
ζM(W)=E{e2(n)}
(16)
其表征為抗干擾后信號與預期導航信號的最小均方誤差。當代價函數越小時,抗干擾模塊對于導航信號的保存完好性越強,而對除導航信號以外的干擾的濾除效果越好,即代價函數是評價LMS算法抗干擾效果的根本指標[22]。
LMS算法采用的最優準則為MMSE準則,其收斂后的最優權向量趨近于經典的Wiener-Hopf方程的解[23]:
(17)
得到抗干擾濾波器最優時的維納濾波器最小代價函數:
(18)
當LMS算法可收斂且自適應循環次數趨于無窮大時,抗干擾濾波器的解接近于維納解Wopt,但是與維納解之間存在額外均方誤差(excess mean square error, EMSE),因此LMS算法具有次優性[24]。抗干擾算法收斂后的均方誤差可以表示為最小均方誤差和額外均方誤差之和:
ξM=minζM+ζex(∞)
(19)
將minζM和ζex(∞)的比值定義為失調,表征抗干擾后的穩態誤差與維納解的差別:
(20)
經典LMS算法中,失調量ΜM已由Widrow推導出:
(21)
其中,算法收斂需滿足的條件為:
(22)
式中,tr(Rx)為輸入信號自相關矩陣的跡,即為輸入信號的總功率,可用集平均特征值λav表征:
(23)
(24)
式中,r(0)為Rx主對角線元素,τav為算法收斂的平均時間常數。
失調與濾波器階數以及收斂速度之間的關系可以表示為:
(25)
由式(24)和式(25)即可得到抗干擾后的導航信號均方誤差:
(26)
最小均方誤差minζM是關于濾波器階數的單調非遞增函數,因此隨著濾波器階數增加,抗干擾濾波器的代價函數減小,即抗干擾性能不斷提升。當濾波器階數過小時,濾波器處于欠擬合狀態,導致LMS算法發散,會引起較大的抗干擾誤差。而當濾波器足夠長時,由階數增加引起的最小均方誤差減小微乎其微,其增加了復雜度的同時還會使得穩態誤差變大。
但由式(26)可知,均方誤差表達式中含有同比參數M,使代價函數存在以濾波器階數的二次速率下降的可能性,即產生自適應噪聲。在同輸入導航信號和同迭代步長時,階數增加使得輸入信號總功率增加,生成更大穩態誤差。
因此,時域抗干擾濾波器性能與濾波器階數呈整體遞增然后趨于平穩的關系,并在性能增加時存在穩態誤差和局部最優性導致的數據波動。如圖3所示,基于LMS算法的抗干擾濾波器在時間域內對信號特征做相關,在干擾信號所在頻帶形成零陷,當濾波器階數增加時,濾波器過渡帶壓縮,阻帶向干擾信號頻帶集中,因此有用信號損耗減小,且幅頻響應的零陷加深,對干擾信號的抑制比增加,從而獲得更好的抗干擾性能;當濾波器長度繼續增加時,零陷與過渡帶改善不明顯,抗干擾性能的提升效果降低。
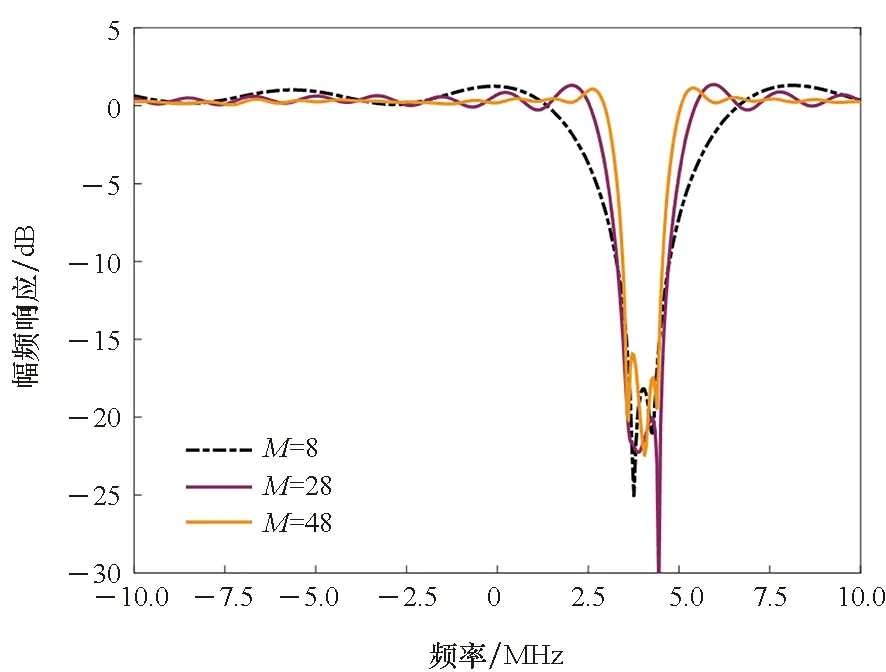
圖3 幅頻響應Fig.3 Amplitude frequency response
由式(22)和式(23)得到,迭代步長滿足的收斂條件同濾波器階數呈反比,當階數增大時,迭代步長滿足收斂的最大值降低,使得收斂條件更加嚴格:
(27)
因此,當濾波器階數增加而步長不變時,算法收斂時間變長,當收斂速度減緩到一定程度而無法在規定迭代次數實現收斂時,則會影響抗干擾性能以及抗干擾是否實現。如圖4所示,對于規定的步長值,抗干擾濾波器在階數為8時快速收斂,隨著階數增加,收斂時間變長,當濾波器階數為48時,濾波器權值在迭代結束時仍在繼續收斂,可見其抗干擾性能明顯變差;當步長增加時,同長度抗干擾濾波器的穩態噪聲變大,收斂條件更為嚴格,導致抗干擾性能下降;當步長增加到20×10-6時,抗干擾濾波器在48階時發散。
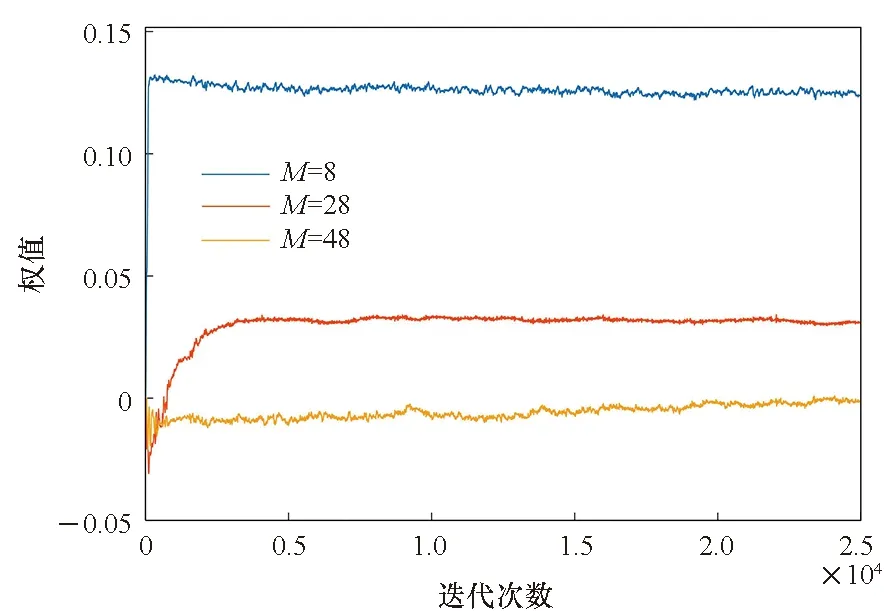
(a) μ=5×10-6
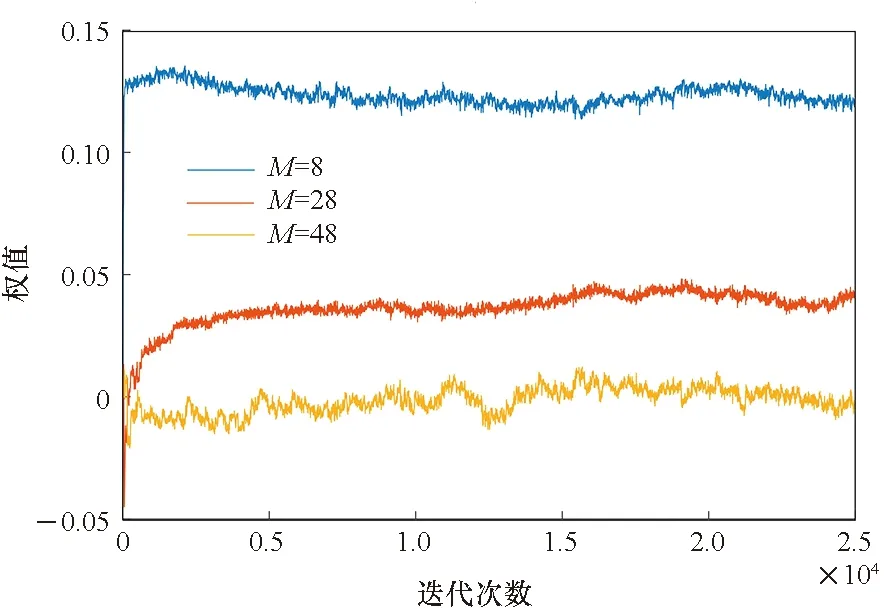
(b) μ=17×10-6
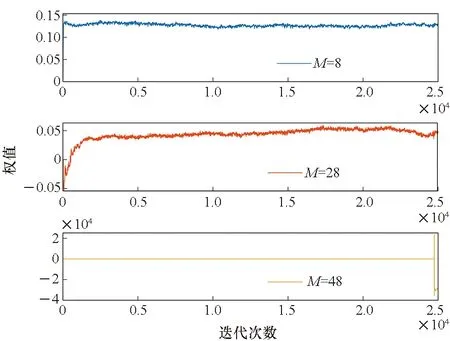
(c) μ=20×10-6圖4 濾波器階數與步長的相互影響Fig.4 Interaction between filter order and step size
2.2 濾波器階數面向不同干擾的影響差異分析
導航信號的擴頻特性導致抗窄帶干擾表現為帶阻濾波器,當濾波器階數相同時,LMS算法抗干擾性能面向不同功率、不同帶寬干擾表現出不同的阻帶衰減特征[25]。

p(j)=E{x(n)s*(n-j)}
(28)
r(i)=E{x(n)x*(n-i)}
(29)
則最小代價函數可以表示為:
minζ(W)=E{s2(n)}-
(30)
由于信號、干擾和噪聲互不相關,p(·)即為期望信號的自相關函數:
p(j)=E{s(n)s*(n-j)}
(31)
因此,rxd在導航信號不變的前提下不受干擾信號參數影響,最小代價函數受干擾影響的可調項僅為Rx[26]。
干擾信號功率峰值與噪底的差值用干信比JSR表示,信號與噪聲功率的差值用信噪比SNR表示,窄帶干擾信號的干擾相對帶寬為η,當干擾相對帶寬小于20%時,干擾信號為窄帶信號[27]。
自相關矩陣的對角線元素可以表示為:
(32)
當干擾信號功率或帶寬增加時,r(0)增大,自相關矩陣的其他矩陣元素也有同樣的變化趨勢,則最小代價函數增大,即抗干擾性能降低[28]。
干擾信號功率越高,同長度濾波器的抗干擾效果越差,且有限長濾波器能達到的抗干擾極限性能越低。圖5是不同干信比條件下同長濾波器抗干擾前后的頻譜圖和幅頻響應:當干擾功率增大時,抗干擾后的零陷深度基本一致,但濾波器頻率響應的過渡帶明顯拉寬,導航信號損耗增多導致抗干擾性能下降。

(a) JSR=40 dB

(b) JSR=50 dB

(c) 幅頻響應對比(c) Comparison of amplitude-frequency response圖5 干信比對同長濾波器性能的影響Fig.5 Influence of JSR on the anti-jamming performance of the filter with same length
干擾信號的相對帶寬越大,干擾信號逐漸喪失窄帶特征而向寬帶干擾過渡,導航信號損耗導致的抗干擾效果降低程度逐漸超出抗干擾實際需求,因此自適應濾波器的抗干擾效果越差,且抗干擾極限性能降低。圖6是干擾相對帶寬分別為5%和10%下的抗干擾前后頻譜圖和幅頻響應:干擾相對帶寬增加對自適應濾波器的頻率響應過渡帶和零陷不造成明顯影響,但是由于在干擾頻帶范圍內的導航信號和加性噪聲被損耗,實際抗干擾效果明顯變差,且抗干擾極限性能降低。
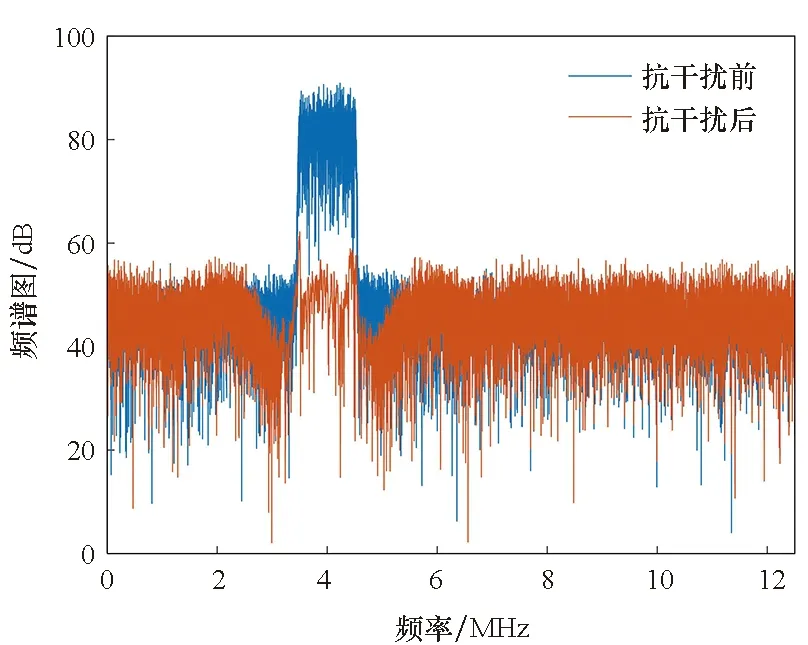
(a) η=5%
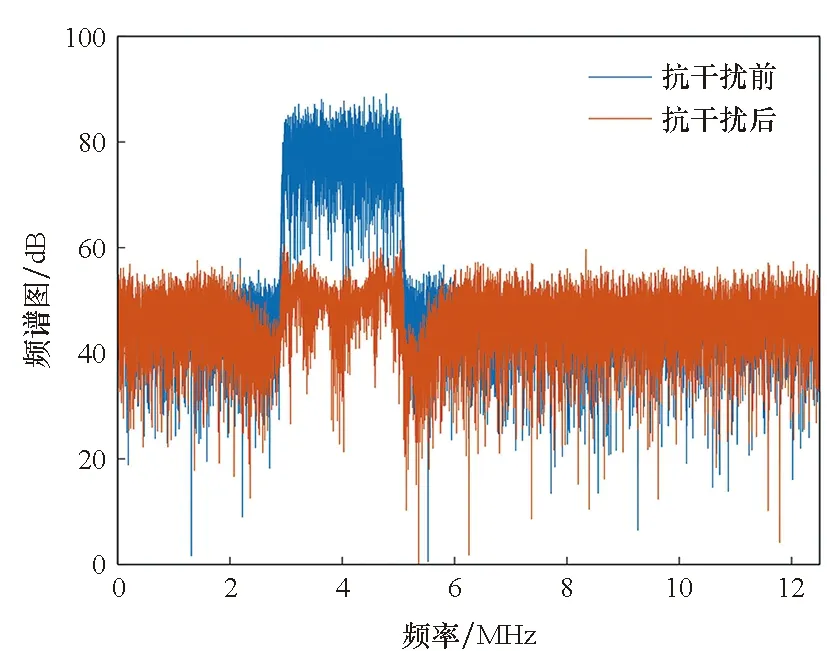
(b) η=10%
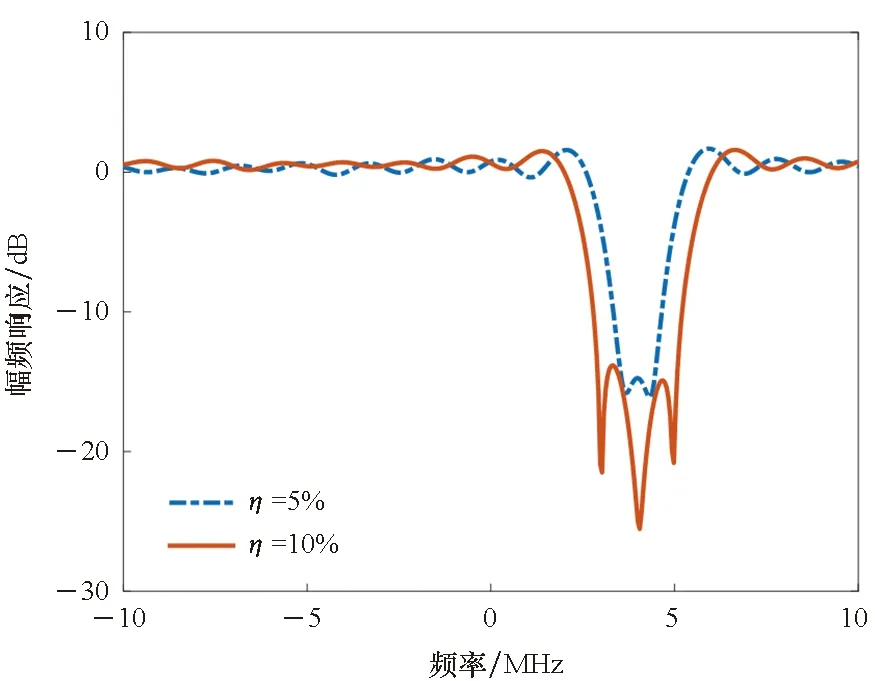
(c) 幅頻響應對比(c) Comparison of amplitude-frequency response圖6 干擾相對帶寬對同長濾波器性能的影響Fig.6 Influence of interference bandwidth on the anti-jamming performance of the filter with same length
3 抗干擾性能驗證
3.1 仿真實驗
3.1.1 經典LMS算法
當原始信號載噪比為45 dB-Hz時,首先分析維納濾波器的抗干擾性能,設定干信比為50 dB。如圖7所示:維納濾波器的抗干擾性能隨階數變化呈整體遞增趨勢,隨著濾波器階數持續增加,載噪比提升空間受干擾限制,抗干擾性能趨于穩定,不再有明顯改善;由于不同階數濾波器的維納解之間相互獨立,其濾波權向量之間不存在必然聯系,因此存在數據波動。

圖7 維納濾波器抗干擾性能Fig.7 Interference suppression performance of Wiener filter
LMS自適應濾波器的收斂程度和抗干擾性能受濾波器階數、迭代次數和收斂步長等因素影響,最優權向量難以徹底收斂到維納解,因此其抗干擾性能與濾波器長度并不是單調遞增關系,而是趨向圖7中所示的關系,且抗干擾性能低于維納解。如圖8所示:基于經典LMS算法的抗干擾性能隨濾波器階數的變化趨勢整體遞增,但存在一定的數據波動;當干擾相對帶寬和干信比增大時,抗干擾需求增大且干擾帶來的不確定性增加,導致數據波動也隨之增大。
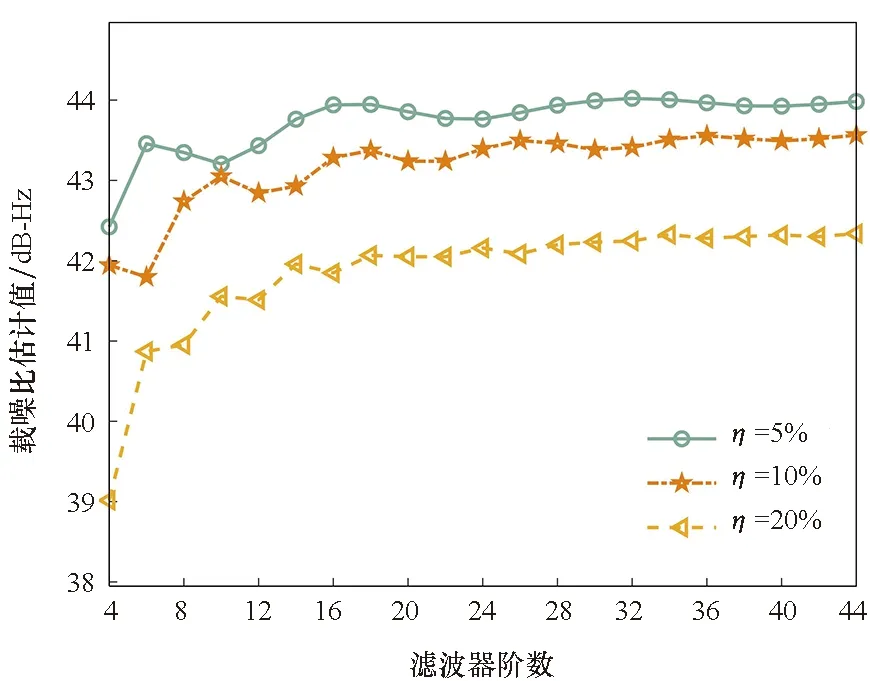
(a) 不同干擾帶寬 (JSR=50 dB)(a) Different bandwidth (JSR=50 dB)

(b) 不同干信比(η=5%)(b) Different JSR(η=5%)圖8 濾波器階數對抗干擾性能的影響Fig.8 Influence of filter order on the interference suppression performance
當濾波器階數足夠長時,抗干擾性能提升空間忽略不計,而相同干擾環境下不同長度濾波器可獲得的最大載噪比估計值即為抗干擾極限性能。圖9為時域抗干擾在不同干擾環境中的抗干擾極限性能,無干擾載噪比為45 dB-Hz。如圖9所示,隨著干擾相對帶寬和干信比增加,導航信號的損耗不斷增長,時域抗干擾的極限性能降低;時域抗干擾只能抑制窄帶干擾,當干擾帶寬超出導航信號帶寬的20%時,抗干擾逐漸失效。
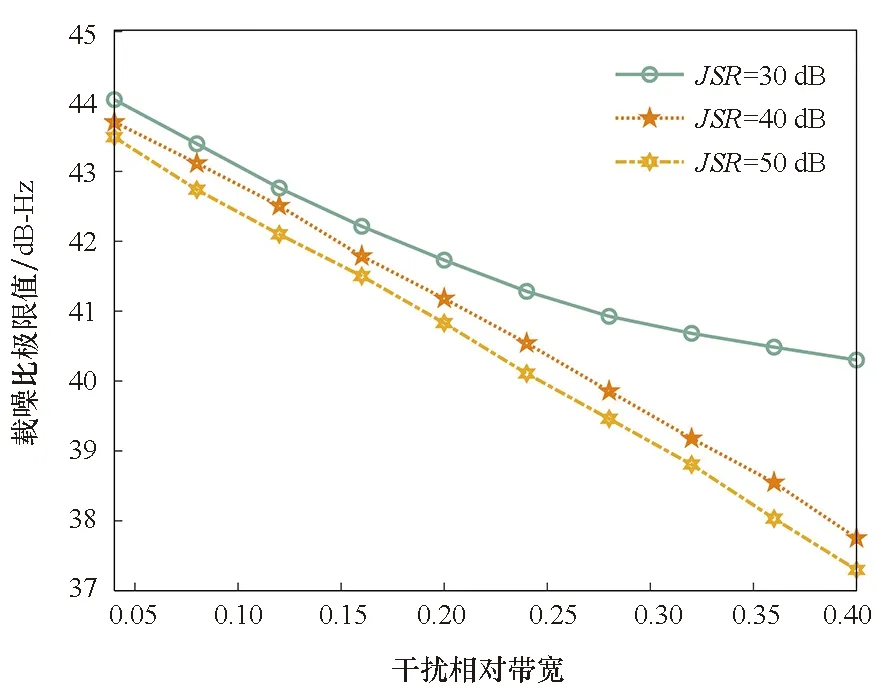
圖9 抗干擾極限性能Fig.9 Ultimate interference suppression performance
為驗證自適應算法收斂不足導致的數據波動問題,通過LMS算法不同階數濾波器的權向量補零迭代,分析濾波器階數對時域抗干擾的影響。此時,M階濾波器的權向量初始值通過M-1階濾波器收斂后的最優權向量補零獲得:
(33)
式中,濾波器階數M的初始值選取最小值2。
圖10為濾波器權向量補零迭代后的抗干擾性能曲線,已知干信比為50 dB。該圖表明,抗干擾性能隨濾波器階數變化曲線的數據波動源于各階濾波器參數間的獨立推導;當通過濾波權向量補零迭代使濾波器系數與每一階濾波器相關時,抗干擾性能隨濾波器階數呈單調遞增趨勢,抗干擾性能出現迭代增加的特點,且優于LMS算法,但是權向量迭代使得收斂速度大大降低。
3.1.2 改進型LMS算法
變步長LMS算法的改進重點是減小穩態誤差和加快收斂速度,穩態誤差決定了抗干擾性能而收斂速度反映信息處理速度,但其理論最優仍是維納解。對幾種改進型LMS濾波器的階數對抗干擾性能的影響關系進行驗證,其抗干擾性能隨濾波器階數的變化趨勢應和維納濾波器以及LMS算法保持基本一致。假設仿真實驗中的窄帶干擾干信比為50 dB,干擾帶寬為5%,同一算法的步長參數μ0不變,對不同改進算法在不同濾波器階數下的抗干擾性能進行驗證。
當步長參數不變時,濾波器抗干擾能力受濾波器階數的影響,且影響程度受制于步長導致的收斂程度。圖11~13是NLMS算法、NVLMS算法和新變步長LMS算法在濾波器階數為10和30時的頻率響應和收斂性能。各圖表明,同一步長參數可使長濾波器更快收斂,短濾波器由于未收斂而抗干擾性能變差;當濾波器增加同樣長度時,新變步長LMS算法的幅頻響應優化程度小于NLMS算法和NVLMS算法,但其低階濾波器收斂性明顯優于另外兩者。

(a) 幅頻響應(a) Amplitude-frequency response
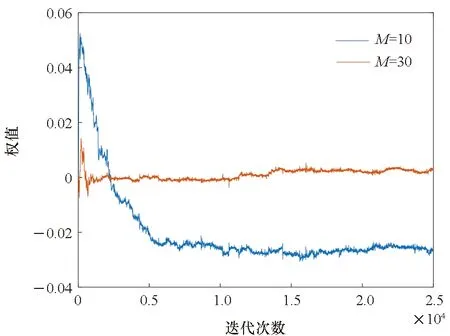
(b) 收斂性能(b) Convergence performance圖11 NLMS算法性能Fig.11 Performance of NLMS algorithm

(a) 幅頻響應(a) Amplitude-frequency response

(b) 收斂性能(b) Convergence performance圖12 NVLMS算法性能Fig.12 Performance of NVLMS algorithm

(a) 幅頻響應(a) Amplitude-frequency response
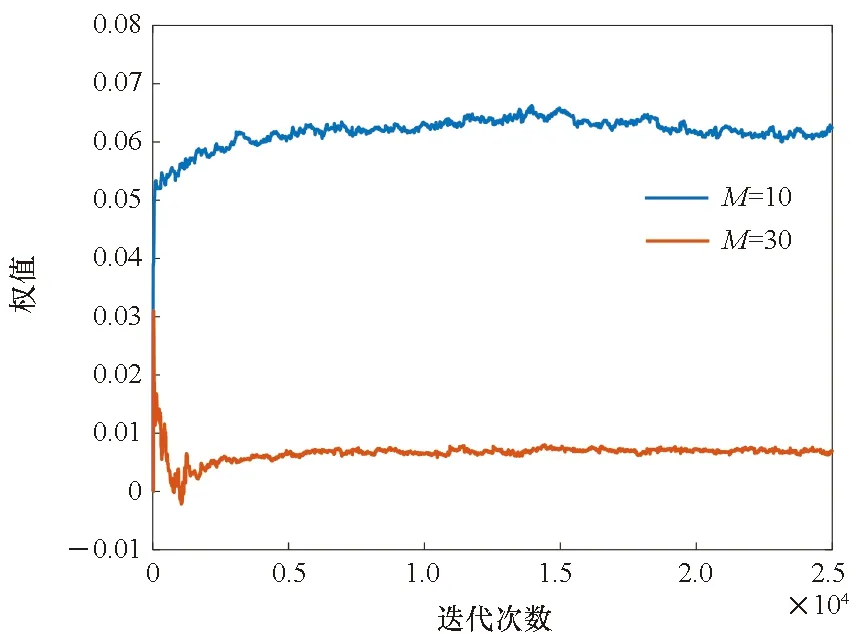
(b) 收斂性能(b) Convergence performance圖13 新變步長LMS算法性能Fig.13 Performance of new variable-step LMS algorithm
不同改進算法在不同濾波器階數下的抗干擾性能如圖14所示,不同的改進型LMS算法的穩態誤差各有差異,但抗干擾性能與濾波器階數關系仍保持總體上升、存在數據波動的變化趨勢。NLMS算法和NVLMS算法都有較好的抗干擾性能,且性能曲線波動較小,而新變步長LMS算法由于受到多個可變參數制約,在恒參數條件下產生了較大的曲線波動。
綜上所述,表1基于濾波器階數影響分析對文中幾種自適應算法的性能進行了總結,包括抗干擾性能隨濾波器階數增加是否穩定、除濾波器階數外的可變參數數量以及參數復雜度導致的抗干擾性能是否可控。
3.2 實測驗證
為了驗證本文理論分析和仿真實驗在導航接收機實際場景下的適用性,在多種窄帶干擾環境下進行了實測,所采數據為從北斗導航系統7號星發回的B3民用信號。此次共測試干擾帶寬與干信比為1 MHz/40 dB、1 MHz/50 dB、2 MHz/40 dB、2 MHz/50 dB的四個場景,數據長度為1 ms,采樣率為75.12 MHz,無干擾信號載噪比為58 dB-Hz。搭建的實測平臺如圖15所示。

圖15 實測平臺Fig.15 Platform of the practical test
抗干擾性能隨濾波器階數的變化曲線如圖16所示,主要采用NLMS算法:性能影響曲線呈現總體遞增趨勢,但恒步長限制了算法的收斂程度,從而產生了數據波動;帶寬和功率更小的干擾更易快速收斂,從而不易受到恒步長制約,例如,2 MHz/50 dB干擾場景下的抗干擾性能曲線比其他干擾有更明顯的波動走勢。
針對上述寬帶寬、高功率干擾場景下的抗干擾性能曲線波動問題,對步長制約因素進行驗證,主要針對不同恒步長下NLMS算法進行實驗,對2 MHz/50 dB干擾進行抑制。如圖17所示,步長分別為0.01、0.02、0.05、0.08時,性能曲線下降處的濾波器階數不同,極限抗干擾性能處的濾波器階數也不同;此外,有限長濾波器的極限抗干擾性能最大差值為2.21 dB,這是由恒步長可能無法滿足有限長濾波器的收斂條件導致的。
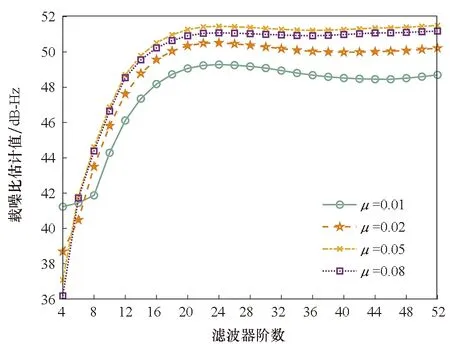
圖17 恒步長對抗干擾性能曲線的影響Fig.17 Influence of constant step size on the interference suppression performance
由于算法結構的不同,持續增加濾波器階數并不能保證穩定的性能提升,圖18對經典LMS算法和三種改進型的LMS算法的抗干擾性能曲線進行了對比。對比幾種算法采用有限長濾波器階數時的極限抗干擾性,NLMS算法和NVLMS算法的收斂性都要優于傳統LMS算法,其中NVLMS算法受恒參數制約影響更大。新變步長LMS算法則呈現較大的數據波動,由于可變參數多,且無法自適應地隨干擾信號以及濾波器階數進行調整,無法在恒參數條件下始終通過增大濾波器長度來提高抗干擾性能。
4 最優濾波器階數
現有已知的變階數LMS算法雖然在自適應領域濾波器階數控制方面取得了較大發展,但在導航接收機領域應用時出現了工程不易實現、無法直接體現抗干擾需求等缺陷[29]。例如,分割濾波器LMS算法(segment filter LMS, SF-LMS)需要高速改變硬件結構,在工程上很難實現,且可變參數多導致難以控制性能,無法應對復雜多變的干擾環境[30];梯度下降LMS算法(gradient descent LMS, GD-LMS)相對前者簡單易實現[31],分數階數LMS算法(fractional tap-length LMS, FTLMS)的分數原則增加了算法靈活性和收斂性,但應用到導航接收機仍無法將濾波器設計與抗干擾需求直接關聯[32]。
導航時域抗干擾濾波器的最優階數選取需要以滿足抗干擾需求為目的,而通過第2節的分析可知,復雜干擾條件下所需的濾波器階數也是變化的。因此,需要根據干擾信號特征自適應調整抗干擾濾波器階數,窗函數法是一種有效的時域數字濾波器設計方法。
窗函數法通過采用不同有限時寬的窗函數截短無限長序列,從而得到有限長序列,實現相應的有限沖激響應濾波器。在眾多窗函數中,凱澤窗法可以通過階數調整主瓣寬度和旁瓣衰減,因此能設計滿足抗干擾需求的最短濾波器[33]。
凱澤窗由貝塞爾函數構成,含有復雜可變的窗形參數α,但是可以實現同等性能下最陡峭的窗函數過渡帶:
(34)
式中:α為可調窗形函數,可以同時調整主瓣寬度和旁瓣衰減;Ι0(α)是第一類變形零階貝塞爾函數。其傅里葉變換為W(ω)。
結合導航信號特點,凱澤窗法設計的數字濾波器階數與干信比JSR、過渡帶寬Δf、采樣率fs的關系為:
(35)
由式(35)可知,可以通過調節階數控制濾波器性能:
(36)
并由此得到濾波器的歸一化上下截止頻率ωa1、ωa2。
理想抗干擾濾波器頻響為:
(37)
則抗干擾濾波器的頻率響應為:
(38)
抗干擾性能通常用載噪比損耗這一指標量化,當無干擾條件下的載噪比與抗干擾后載噪比估計值的差值小于實際需求時,即滿足抗干擾需求:
ΔCNR=[C/N]0-[C/N]ajm
(39)
Mmin=min{M|ΔCNR≤κ}
(40)
Mmin即為可變干擾環境下的自適應最優濾波器階數。
5 結論
針對衛星導航接收機時域抗干擾中,基于抗干擾性能的濾波器階數影響分析不足的現狀,面向不同干擾環境和相關算法,分析了濾波器階數對時域抗干擾性能的影響,并簡易提出了一種自適應的最優濾波器階數設計方法。實驗結果表明,導航接收機的時域抗干擾性能受濾波器階數的影響如下:
1) 時域抗干擾性能隨濾波器階數的變化趨勢呈整體遞增、存在數據波動的趨勢。適當提升濾波器長度,可以有效提升時域自適應濾波器的抗干擾性能。
2) 抗干擾性能隨濾波器階數變化的數據波動來源于步長參數導致的收斂性不夠。
3) 改進型LMS算法的性能提升受濾波器階數影響各不相同,但性能變化趨勢同維納濾波器保持基本一致。
本文可以為導航接收機低復雜度的時域抗干擾研究提供明確的理論支撐,解決工程中階數選取嚴重依賴實踐經驗而影響分析不足的問題,可以為導航接收機抗干擾模塊的硬件優化提供借鑒。后續工作可根據第4節中提出的思路,進一步研究導航接收機時域抗干擾的最優濾波器階數,即根據實際抗干擾需求,自適應地調整濾波器階數,使其靈活應對復雜多變的干擾環境。

