改進Laplace先驗下的復數域多任務貝葉斯壓縮感知方法*

張啟雷,孫 斌

(1. 國防科技大學 電子科學學院, 湖南 長沙 410073; 2. 北京跟蹤與通信技術研究所, 北京 100094)

稀疏貝葉斯學習(sparse Bayesian learning,SBL)理論已經發展成為信號處理領域的一個重要分支[1-4]。SBL理論與壓縮感知相結合催生了一類重要的稀疏信號重構算法,即貝葉斯壓縮感知(Bayesian compressive sensing,BCS)方法[5-7]。BCS方法的應用領域相當廣泛,包括陣列設計、波束形成和雷達成像等[8-10]。

SBL又被稱為相關向量機(relevance vector machine,RVM),具有良好的全局最優和局部最優特性[3]。研究表明,SBL等價于一種加權的1范數算法,因此是一類精確性和魯棒性更好的稀疏重構算法[11]。文獻[5]將SBL理論應用到壓縮感知領域,并提出了BCS技術。隨后,BCS被進一步擴展到多任務壓縮感知領域[6]。文獻[7]基于分層Laplace先驗分布,提出了一種改進的BCS方法。基于上述研究,實數域的BCS理論框架已經基本完善了。然而,現有的實數域BCS方法無法直接解決復數域稀疏信號重構問題。

為了利用BCS理論實現復數域稀疏信號重構,文獻[12-13]給出了一種直觀的解決思路,即將復數分解為實部和虛部,分別利用現有的實數域BCS方法進行求解,最后將兩部分結果合成為復數。在此基礎上, 文獻[14]假設復數的實部和虛部具有相同的稀疏特性,提出了一種復數域多任務BCS(complex multitask Bayesian compressive sensing, CMT-BCS)算法。然而,由于復數分解,測量矩陣和信號的維度都被擴大了,上述算法的存儲量和計算量明顯增加。此外,復數分解不可避免地破壞了原始復數信號的內部結構,因此稀疏重構結果難以令人滿意。

與上述算法不同,本文直接在復數域推導并構建BCS理論框架。首先,基于改進的分層Laplace先驗和多任務學習模型,建立了復數域貝葉斯壓縮感知模型;其次,通過邊緣積分消除了測量噪聲方差的影響,提出了一種復數域貝葉斯壓縮感知方法;再次,利用矩陣分解理論,推導了一種基于遞歸操作的快速算法;最后,利用數值仿真實驗驗證了本文提出的改進Laplace先驗下的復數域多任務貝葉斯壓縮感知(complex multitask Bayesian compressive sensing algorithm using modified Laplace priors, CMBCS-MLP)方法的有效性。

1 問題描述

1.1 多任務學習模型

本文考慮一種多任務學習場景,假設不同任務之間是統計相關的,且共享相同的先驗參數。復數域多任務貝葉斯測量模型可以表示為

yi=Φixi+ni

(1)

其中:i=1,2,…,L表示任務索引,L代表任務數目;yi∈Ni表示復數域壓縮觀測數據,Φi∈Ni×M表示復數域測量矩陣,xi∈M表示復數域原始信號,ni∈Ni代表復數域測量噪聲,Ni?M。

根據BCS理論框架,如果xi滿足某種合適的稀疏先驗分布,則可以利用貝葉斯原理得到該信號的后驗概率,進而從壓縮后的觀測數據yi中恢復出稀疏原始信號xi[1-3]。

1.2 改進的分層Laplace先驗

根據貝葉斯理論觀點,所有的未知變量均可以看作滿足一定概率分布的統計量[1,15]。

首先,假設ni滿足零均值復高斯分布,且方差為σ2。令β=σ-2,則復數域觀測數據的條件概率分布函數可以表示為

p(yi|xi,β)=CN(yi|Φixi,β-1)

(2)

其中,CN(·)代表多變量復高斯分布,先驗參數β滿足Gamma先驗分布

(3)

然后,假設原始信號xi滿足某種稀疏先驗分布。文獻[7]已經證明,相比于RVM中的先驗分布[1],分層Laplace分布是一種性能更優的先驗分布。然而,直接沿用文獻[7]提出的分層Laplace先驗設置得到的BCS算法受測量噪聲方差,即先驗參數β的影響。如果β的初始值設置不合理,BCS算法存在性能惡化的危險。然而,通過改進原始信號xi的先驗分布形式,可以消除參數β的影響,進而得到一種改進的BCS算法[6]。

第一層,假設xi滿足特殊的多變量零均值復高斯分布

(4)

其中,α為先驗參數,|xi,m|表示xi的第m個元素的絕對值。 第二層,假設α先驗參數滿足一種特殊的Gamma分布

(5)

其中,αm>0,且λ>0。 綜上,原始信號xi的先驗分布可以表示為

可以看出,經過分層先驗設置,復數域原始信號xi滿足Laplace先驗分布。第三層,假設超先驗參數λ滿足一種特殊分布p(λ)=1/λ[7]。

綜上,圖1給出了基于改進的分層Laplace先驗的復數域多任務學習貝葉斯模型圖。可以看出,該貝葉斯模型分為三層:底層為復數域多任務信號模型,中間層為由多個任務共享的先驗參數,頂層為超先驗參數,用來控制中間層的先驗參數。本文中先驗參數和超先驗參數同稱為超參數(hyper-parameters)。

圖1 基于改進Laplace先驗的復數域多任務貝葉斯壓縮感知模型圖Fig.1 The graphical model of complex multitask Bayesian compressive sensing using modified Laplace priors

2 CMBCS-MLP方法

2.1 貝葉斯推斷

根據BCS理論,原始信號的稀疏重構是通過使其后驗概率最大得到的。圖1中未知變量的后驗概率分布可以表示為

(7)

其中,{xi}和{yi}分別代表原始信號集和觀測數據集。通常,很難直接得到p({xi},α,β,λ|{yi})的解析表達式[1]。然而,根據貝葉斯原理

p({xi},α,β,λ|{yi})

=p({xi}|{yi},α,β,λ)·p(α,β,λ|{yi})

(8)

根據式(8),可以得到一種實用的貝葉斯推斷方法。

假設超參數α和β已知,則原始信號xi的后驗概率分布可以表示為

(9)

根據式(2)和式(4),可以得到

p(xi|yi,α,β)=CN(xi|μi,β-1Σi)

(10)

其中

(11)

A=diag(α1,α2,…,αM)是對角矩陣。

進而,基于1.2節建立的特殊先驗分布,可以通過邊緣積分消去參數β的影響,即

(12)

可以看出,通過邊緣積分消去超參數β之后,xi的后驗概率分布從式(10)給出的多變量復高斯分布變為式(12)給出的多變量Student-t分布[6]。 根據Student-t分布的性質,xi的后驗期望仍然為μi。 然而,相比于高斯分布,Student-t分布具有更尖銳的峰值和更長的拖尾[1,6],這意味著改進后的算法具有更好的稀疏重構性能。 此外,消除了測量噪聲方差的影響之后,式(12)中給出的稀疏重構算法魯棒性更好。

2.2 超參數估計

本節基于經驗貝葉斯(empirical Bayesian)方法[1],給出超參數估計方法。 為了估計超參數α和λ,需要利用所有的觀測數據集{yi}。 根據貝葉斯原理,p(α,λ|{yi})∝p({yi},α,λ),且

(13)

因此,通過使p({yi},α,λ)最大化可以得到上述超參數的點估計值。

根據式(2)和式(3),可以得到

=CN(yi|0,β-1Bi)

(14)

(15)

為了方便推導,下面將p({yi},α,λ)的對數值作為代價函數

L(α,λ)=lnp({yi},α,λ)

(16)

其中,C為常數。對L(α,λ)分別關于αm和λ求導,并令導數為零,可以得到兩者的點估計值為

(17)

然而,需要指出的是,上述迭代算法涉及矩陣求逆運算,運算量較大。尤其對于高維度的信號,該算法的運算量是難以承受的。因此,為了提高該算法的實用性,有必要研究其快速算法。

3 基于矩陣分解理論的快速算法

如前所述,在迭代算法中,最主要的計算量來自式(11)中Σi的求解,不僅涉及矩陣求逆運算,還需要在每次迭代中更新α中全部的元素。事實上,文獻[2]已經證明,更新α中單個元素也可以實現代價函數L(α,λ)的有效更新。因此,通過序貫地增加、刪除或重新估計α中的某一個元素,可以實現超參數α的有效估計,最終找到原始信號xi中所有有效的xi,m,即實現稀疏重構。

3.1 算法推導

根據矩陣分解理論[2],矩陣Bi可以寫為

(18)

(19)

只考慮L(α,λ)中α的影響,則可以得到

L(α)=L(α-m)+(αm)

(20)

其中,L(α-m)與αm無關,而(αm)可以表示為

(21)

其中

(22)

因此,可以得到

(23)

理論上,令式(23)等于零可以得到αm的點估計值。然而,除αm=∞這個解之外,很難得到αm的其他解析解。文獻[2]已經證明,通常αm?si,m,因此可以得到

(24)

其中

(25)

通過求解式(24),可以得到αm的近似解為

(26)

基于式(26),可以得到一種基于遞歸操作的復數域多任務貝葉斯壓縮感知快速算法。在每次的遞歸操作中,只需要更新一個候選的αm,因此μi和Σi的更新很高效,同時λ也可以同步更新。實際中,通常選擇使(αm)值最大的αm作為候選參數,可以獲得更快的收斂速度[5-7]。

3.2 誤差分析

在上述推導中,為了得到αm的解析解,假設αm?si,m,進而得到近似等式(24),因此必須分析該假設帶來的近似誤差。

在式(23)的基礎上,進一步求解代價函數L(α)的二階導數可得

(27)

然而,上述分析是建立在假設αm?si,m的基礎之上的。雖然文獻[2]和文獻[6]已經證明了該假設的有效性,但只能保證式(26)給出的近似解位于(αm)的局部最大值點附近,因此上述近似處理是次優的。盡管如此,已有文獻[2,5-7]和本文的數值仿真均表明上述快速算法的精確性和有效性是足夠的。

3.3 計算復雜度分析

本節基于矩陣分解理論推導了一種基于遞歸操作的快速算法,相比于第2節的迭代算法,可以有效降低計算復雜度。

針對第2節給出的迭代算法,最主要的計算量來自式(11)中的矩陣求逆。矩陣Σi的維度為M×M,因此求逆運算的計算復雜度為Ο(M3)[5]。隨著M的增大,該計算復雜度急劇增加。本節提出的快速算法采取遞歸操作,每次只針對α中的一個元素進行計算,直到找到α中所有的有效元素,操作次數近似等于壓縮觀測數據的維度Ni。詳細分析表明[2]:基于遞歸操作的快速算法的計算復雜度為Ο(NiM2)。由于Ni?M,因此相比于第2節的迭代算法,本節給出的快速算法計算復雜度大大降低。

4 數值仿真

單任務學習可以視作多任務學習的特例, CMBCS-MLP方法同樣適用于單任務學習場景,此時令L=1即可。首先,面向單任務學習場景,針對兩種不同的復數域信號進行稀疏重構實驗,并與文獻[12-13]給出的實數域BCS方法 (記為RBCS)和文獻[14]提出的CMT-BCS方法的重構結果進行對比。為了便于對比,在仿真中,a=100/E{VAR(yi)},b=1,其中VAR(·)代表求方差,E{·}代表求均值。

第一種信號為復數域均勻尖峰信號,長度M=512,其實部和虛部分別包含30個位置隨機出現的尖峰,尖峰幅度為1或-1。測量矩陣Φi的生成分為兩步:首先,生成服從復高斯分布CN(0,1),維度為Ni×M的復矩陣,Ni=100;然后,對該復矩陣沿行進行幅度歸一化處理。測量噪聲ni的實部和虛部均滿足零均值高斯分布,且標準差為σ=0.005。稀疏重構實驗的結果如圖2所示,由于篇幅所限,圖中只給出了復數域信號的幅度。其中RBCS、CMT-BCS、CMBCS-MLP方法的重構誤差分別為eRBCS=1.226 7、eCMT-BCS=0.255 3、eCMBCS-MLP=0.016 9。

(a) 原始信號(a) Original signal

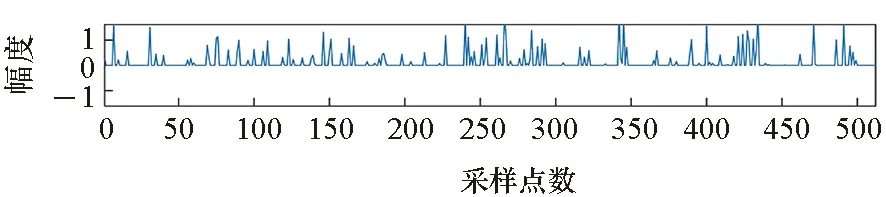
(b) RBCS方法重構結果(b) Reconstruction result using RBCS

(c) CMT-BCS方法重構結果(c) Reconstruction result using CMT-BCS

(d) CMBCS-MLP方法重構結果(d) Reconstruction result using CMBCS-MLP圖2 復數域均勻尖峰信號重構結果 (Ni=100, M=512)Fig.2 Reconstruction result of complex uniform spikes(Ni=100, M=512)

第二種信號為復數域非均勻尖峰信號,長度M=512,其實部和虛部分別包含30個位置隨機出現的尖峰,尖峰的幅度滿足零均值高斯分布,且與均勻尖峰信號的功率相等。測量矩陣Φi和測量噪聲ni的生成方法與前文相同。稀疏重構實驗的結果如圖3所示。其中RBCS、CMT-BCS、CMBCS-MLP方法的重構誤差分別為eRBCS=0.023 5、eCMT-BCS=0.099 5、eCMBCS-MLP=0.015 5。

(a) 原始信號(a) Original signal

(b) RBCS方法重構結果(b) Reconstruction result using RBCS

(c) CMT-BCS方法重構結果(c) Reconstruction result using CMT-BCS

(d) CMBCS-MLP方法重構結果(d) Reconstruction result using CMBCS-MLP圖3 復數域非均勻尖峰信號重構結果(Ni =100,M=512)Fig.3 Reconstruction result of complex non-uniform spikes(Ni=100,M=512)

由圖2和圖3可以看出,針對兩種不同的復數域稀疏信號, CMBCS-MLP方法均給出了最優的重構結果。然而,圖2和圖3給出的結果僅是隨機過程的一次實現,不具有普遍意義。此外,除重構精度外,計算耗時也是重構算法的重要指標。分別針對上述兩種復數域稀疏信號,利用蒙特卡羅方法開展重構實驗,實驗重復次數為100次。不同BCS算法的重構性能如表1所示。可以看出: CMBCS-MLP在重構精度和計算耗時兩個方面均是最優算法,而RBCS算法的性能最差。雖然CMT-BCS針對復數域均勻尖峰信號給出了較好的重構結果,但計算耗時是最長的;而對復數域非均勻尖峰信號,CMT-BCS的重構誤差和計算耗時兩項指標均是最差的。究其原因是,RBCS和CMT-BCS算法人為破壞了復數信號的內部結構,造成算法魯棒性較差、耗時較長;而本文提出的CMBCS-MLP算法直接在復數域進行重構,克服了上述缺陷,因此算法魯棒性較好,計算耗時較短。

最后,通過多任務學習模型來驗證CMBCS-MLP方法在多任務學習中的優勢。假設兩個復數域均勻尖峰信號的參數與前文相同,長度均為M=512。一個特殊的設置在于這兩個復數域信號有80%的尖峰位于相同的位置,即二者的相似性為80%。兩個信號的測量次數分別為N1=70和N2=75。測量矩陣Φi和測量噪聲ni的生成方法與前文相同。稀疏重構實驗的結果如圖4所示。可以看出:由于觀測數據較少,觀測噪聲較大,采用單任務學習CMBCS-MLP方法重構結果誤差較大,無法恢復原始信號;而多任務學習CMBCS-MLP方法充分利用了兩個復數域信號之間的相似性,準確恢復了兩個原始信號。

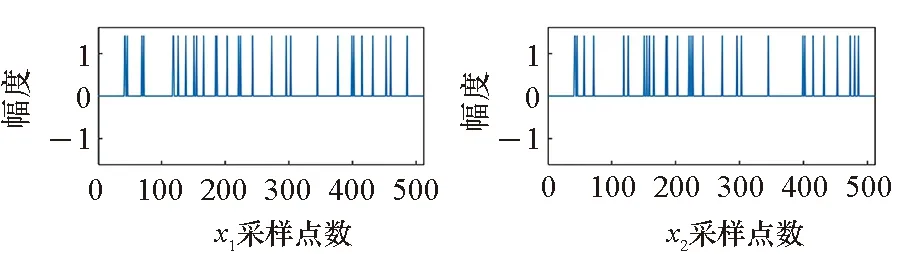
(a) 原始信號x1和x2(a) Original signal x1 and x2

(b) 單任務算法重構結果 x1和x2(b) Reconstruction results of x1 and x2 using single-task algorithm

(c) 多任務算法重構結果x1和x2(c) Reconstruction results of x1 and x2 using multitask algorithm圖4 多任務學習場景下的CMBCS-MLP方法重構結果(Ni=100,M=512)Fig.4 Reconstruction result of CMBCS-MLP for the multitask learning setting (Ni=100,M=512)

5 結論

現有的BCS理論框架是在實數域推導和建立的,因此無法直接用于復數域稀疏信號重構。針對這個問題,本文直接在復數域推導BCS方法。基于改進的分層Laplace先驗和多任務學習模型,本文在復數域推導了一種CMBCS-MLP方法,并基于矩陣分解理論給出了其快速算法。理論分析和數值仿真表明:針對復數域稀疏信號重構問題,相比于現有的實數域BCS方法,CMBCS-MLP方法具有更好的精確性和魯棒性。下一步研究的重點在于將CMBCS-MLP方法應用到具體的復數域信號處理問題中,進一步拓展BCS技術的應用范疇。